زنجیره مارکوف (Markov Approach modeling) قسمت 3
تکامل گذرا
احتمال تغییر حالت از حالت iام به حالت jام در n حرکت برابر است با
این احتمال در یک حرکت برابر است با
برای یک زنجیره مارکوف یکنواخت در زمان
و
توجه کنید که برای یک زنجیره مارکوف یکنواخت در زمان، احتمال تغییر حالت از حالت iام به حالت jام در n حرکت معادل است با درایهٔ (i,j) ام ماتریس احتمال انتقال وقتی این ماتریس n بار در خودش ضرب شدهاست:
در حرکتهای n تایی احتمالات بدست آمده برابری چپمن-کولموگروف را ارضا میکنند. پس برای هر k که ۰ <n> k داریم
در این رابطه S فضای حالت زنجیره مارکوف است. توزیع حاشیه ای (Pr(Xn = x مربوط به حرکت nام است. توزیع اولیه برابر است با (Pr(X۰ = x. تعمیم یافته این توزیع برای حرکتهای بعدی به شکل
نمایش داده میشود که در آن n زیروند است و نه توان.
ردهبندی حالتهای یک زنجیر مارکوف
تقلیلپذیری
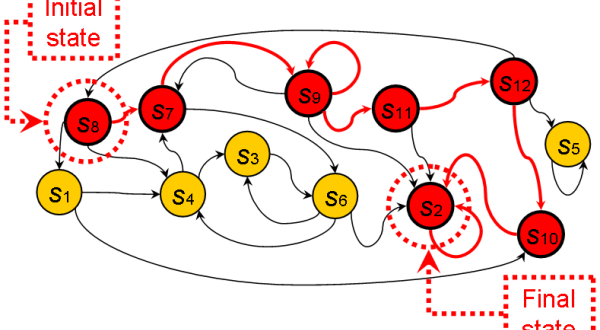
حالت jام را قابل دسترسی از حالت iام مینامند (i → j) اگر در سیستمی که از حالت iام شروع شود با احتمال غیر ۰ در نهایت به حالت jام برسد. در واقع اگر عدد صحیح n ≥ ۰ وجود داشته باشد که
تساوی n با ۰ به معنای در دسترس بودن همه حالات از حالت iام است. حالت iام را مرتبط با حالت jام مینامند (i ↔ j) اگر هر دو رابطه i → j و j → i برقرار باشند.
مجموعه حالات C را کلاس مرتبط مینامند اگر هر یک از اعضای آن با هر عضو دیگر این مجموعه مرتبط باشد و هیچیک از اعضای C با حالتی که عضو آن نیست مرتبط نباشد. میتوان نشان داد که ارتباط همان همارزی است و کلاسهای مرتبط در واقع کلاسهای همارزی هستند.
یک کلاس همارزی را بسته مینامند اگر احتمال خروج از این کلاس ۰ باشد. به عبارت دیگر اگر حالت i در C باشد و حالت j در C نباشد، j قابل دسترسی از i نیست. مجموعهای از کلاسهای مرتبط یک گراف جهتدار بدون دور را تشکیل میدهند که یالهای آن همان یالهای فضای حالت اصلی هستند. یک کلاس مرتبط بستهاست اگر و تنها اگر هیچ یال خروجی میان کلاسهای مختلف وجود نداشته باشد.
حالت i را ضروری مینامند اگر به ازای همه jهایی که i → j، رابطه j → i نیز برقرار باشد. در غیر این صورت حالت i را غیرضروری مینامند.
اگر تمام وضعیتهای یک زنجیر مارکوف با هم مرتبط باشند، فضای حالت تنها از یک کلاس مرتبط تشکیل میشود و به آن تقلیلناپذیر میگویند. در این زنجیرهها از هر حالت میتوان به هر حالتی رسید.
تناوب
حالت i دارای دوره تناوب k است اگر هر مسیر بازگشت به حالت i به طول مضارب k باشد. به زبان دیگر دوره تناوب یک حالت برابر است با
که در آن gcd بزرگترین مقسوم علیه مشترک است. اگر یک حالت دوره تناوب k داشته باشد ممکن است نتوان به این حالت با k حرکت رسید. بهطور مثال اگر بتوان به حالت i در {۶, ۸, ۱۰, ۱۲, …} حرکت بازگشت، در این صورت دوره تناوب برابر ۲ خواهد بود حتی اگر ۲ در مقادیر ذکر شده نباشد. اگر k = ۱ باشد، در این صورت به حالت مد نظر غیر متناوب میگویند و بازگشت به حالت i در حرکتهای غیر منظم انجام خواهد گرفت. در غیر این صورت (k > 1)، حالت iدارای دوره تناوب k و متناوب میباشد.
بازگشتپذیری
فرض کنید fi احتمال این پیشامد باشد که زنجیر با شروع از وضعیت i بعد از تعداد متناهی تغییر وضعیت به i برگردد. به وضوح . اگر در این صورت حالت i را بازگشتی یا پایامیگوییم. به این ترتیب هر بار که زنجیر در حالت i قرار میگیرد فرایند بهطور احتمالی حرکت خود را از سر شروع میکند، لذا اولین بازگشت به i مستلزم بازگشت دوم به i، و الی آخر است؛ بنابراین اگر i حالت بازگشتی باشد، فرایند با احتمال ۱ بینهایت بار به i برمیگردد و احتمال اولین بازگشت به این حالت در زمان متناهی برابر ۱ است. اگر امید ریاضی تعداد تغییر وضعیتها تا بازگشت مجدد به i متناهی باشد به i بازگشتی مثبت و در غیر این صورت بازگشتی پوچ میگوییم.
حالت i را گذرا مینامند هرگاه ، به این معنی که اگر سیستم از حالت i شروع به کار کند، احتمال این که دیگر به این حالت بازنگردد غیر صفر است. برای حالت گذرای i احتمال این که فرایند با شروع از i دقیقاً بعد از n بار به آن بازگردد برابر است با. پس تعداد بازگشتها به i متغیر تصادفی با پارامتر میباشد، درنتیجه تعداد بازگشتها بینهایت نمیشود.
با در نظر گرفتن متغیر تصادفی Ti، زمان اولین بازگشت به حالت i، داریم:
عدد احتمال بازگشت سیستم به حالت i برای اولین بار در حرکت nام است. در نتیجه حالت i گذرا است اگر
متوسط زمان بازگشت
اگر زمان اولین بازگشت به حالت i با احتمال ۱ متناهی باشد، نمیتوان نتیجه گرفت که امید ریاضی این زمان متناهی است. امید ریاضی زمان بازگشت به حالت i همان متوسط زمان بازگشت است که از رابطه
محاسبه میشود.
متوسط تعداد بازگشتها
میتوان نشان داد که حالت i پایا است اگر و تنها اگر متوسط تعداد بازگشتها به این حالت نامتناهی باشد. یعنی
چند قضیه مهم
- اگر i گذرا باشد، زنجیره متناهی بار به i بازمیگردد.
- هر زنجیر مارکوف با فضای حالت متناهی حداقل یک حالت بازگشتی دارد
- بازگشتی بودن یک خاصیت ردهای است یعنی اگر i بازگشتی باشد و با j در ارتباط باشد، آنگاه j نیز بازگشتی است.
- گذرا بودن یک خاصیت ردهای است یعنی اگر i گذرا باشد و با j در ارتباط باشد، آنگاه j نیز گذرا است.
- در هر زنجیر مارکوف تقلیلناپذیر یا تمام حالتها گذرا یا تمام آنها بازگشتی هستند. در هر زنجیر مارکوف تقلیلپذیر، عناصر هر رده یا همه گذرا یا همه بازگشتی هستند. در حالت اول رده را رده گذرا و در حالت دوم رده بازگشتی میگوییم.
- هر زنجیر مارکوف تقلیلناپذیر متناهی، بازگشتی است.
- اگر در زنجیره مارکوف با فضای حالت متناهی بازگشتی باشد، در این صورت حتماً بازگشتی مثبت است.
حالتهای مانا
حالت i را جذبکننده یا مانا مینامند اگر با ورود به این حالت خروج از آن غیرممکن باشد. در نتیجه حالت i مانا است اگر و تنها اگر
اگر هر حالت در یک سیستم به حالت مانایی برسد زنجیره مارکوف را زنجیره مارکوف مانا مینامند.
زنجیره مارکوف (Markov Approach modeling) قسمت 1
زنجیره مارکوف (Markov Approach modeling) قسمت 2
زنجیره مارکوف (Markov Approach modeling) قسمت 3
زنجیره مارکوف (Markov Approach modeling) قسمت 4
زنجیره مارکوف (Markov Approach modeling) قسمت 5





![{\displaystyle p_{ij}^{(n)}=[P^{n}]_{ij}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd3b38dcfe4aa747f5765dbfa1368ae661c7fb65)












![{\displaystyle M_{i}=E[T_{i}]=\sum _{n=1}^{\infty }n\cdot f_{ii}^{(n)}.\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e7182ea52ad054b13097e3b47c7f38fa22bdca87)


دیدگاه خود را ثبت کنید
تمایل دارید در گفتگوها شرکت کنید؟در گفتگو ها شرکت کنید.