مقدمه ای بر فیلترهای خطی حوزه مکان در پردازش تصویر

فیلتر کردن یک تکنیک است که به وسیله ی آن می توان یک عکس را اصلاح کرد و یا کیفیت آن را افزایش داد. بعنوان مثال شما می توانید یک عکس را فیلتر کنید تا برخی از ویژگی هایش را مهمتر جلوه دهید و یا اینکه برخی از ویژگی های آن را حذف کنید. فیلتر کردن، در واقع یک عملیات تقریبی و محدوده ای است به طوری که مقدار به دست آمده برای هر پیکسل از عکس خروجی به وسیله ی اعمال یک یا چند الگوریتم بر پیکسل هایی که در همسایگی پیکسل ورودی قرار دارند، به دست می آید.محدوده یا همسایگی یک پیسکل، در واقع یک مجموعه از پیکسل ها است که موقعیت آنها نسبت به این پیکسل تعریف شده است. اگر مقدار یک پیکسل در خروجی، برابر با یک ترکیب خطی از مقادیر پیکسل های در همسایگی پیکسل ورودی باشد، به این فیلتر، فیلتر خطی گفته می شود.

بررسی در هم پیچیدگی یا convolution

اعمال فیلتر خطی بر روی یک عکس، از طریق یک عملیات به نام در هم پیچیدگی(convolution) انجام می پذیرد. در هم پیچیدگی، نوعی عملیاتِ محدوده ای است، که به وسیله ی آن هر پیکسل خروجی، از جمعِ وزنیِ(weighted sum) پیکسل های در همسایگی پیکسل ورودی به دست می آید.

به ماتریسی که حاوی این وزن ها است، هسته ی درهم پیچیدگی(convolution kernel,) گفته می شود و با نام فیلتر، شناخته می شود. یک هسته ی درهم پیچیدگی(فیلتر)، درواقع یک هسته ی همبستگی(correlation kernel) است که به مقدار 180 درجه چرخیده باشد.

بعنوان مثال، فرض کنید که عکس ما برابر است با:

A = [17 24 1 8 15
23 5 7 14 16
4 6 13 20 22
10 12 19 21 3
11 18 25 2 9]

و هسته ی پیچیدگی(فیلتر) برابر است با:

h = [8 1 6
3 5 7
4 9 2]

عکس زیر نشان می دهد که چگونه پیکسل خروجی $(2,4)$ را با استفاده از توضیحات زیر آن محاسبه کنیم:

 1. ابتدا هسته ی درهم پیچیدگی را به اندازه ی 180 درجه، حول عنصر مرکزی آن بچرخانید. یعنی ابتدا ماتریس A را به اندازه ی 180 درجه بگردانید.

2. عنصر مرکزی هسته ی درهم پیچیدگی(در اینجا یعنی 5)  را در گوشه ی بالا و بر روی عنصر $(2,4)$ از ماتریس A قرار دهید. این موضوع را در عکس بالا به خوبی مشاهده می کنید. همان طور که مشاهده می کنید، مقدار 5، در گوشه ی بالا و سمت راست از درایه ی قرار گرفته در سطر دوم و ستون چهارم ماتریس A قرار گرفته است.

3. حالا هر یک از اندازه ها(وزن ها)ی درون هسته ی درهم پیچیدگی که چرخانده شده است را در پیکسل زیرین خود، از ماتریس A ضرب کنید:

4. حالا مقادیر به دست آمده در گام شماره 3 را با یکدیگر جمع کنید.

بنابراین پیکسل خروجی  $(2,4)$ برابر است با:

بررسی همبستگی یا Correlation

عملیات همبستگی(correlation)، ارتباط نزدیکی با درهم پیچیدگی(convolution) دارد.

در همبستگی نیز، مقدار یک پیکسل در خروجی به صورت جمع وزنی پیکسل های همجوار محاسبه می شود.  اما تفاوت همبستگی در این است که ماتریس وزنی یا همان هسته ی درهم پیچیدگی، به هنگام محاسبه، مورد چرخش واقع نمی شود.

توابع طراحی فیلتر در جعبه ابزار پردازش تصویر متلب، هسته های همبستگی(correlation kernels) را برمی گردانند.

تصویر زیر نشان می دهد که چگونه می توانیم  پیکسل خروجی درایه ی $(2,4)$ از ماتریس A را با استفاده از عملیات همبستگی، محاسبه کنیم. فرض می کنیم که h یک هسته ی همبستگی باشد، بنابراین گام های زیر را انجام دهید:

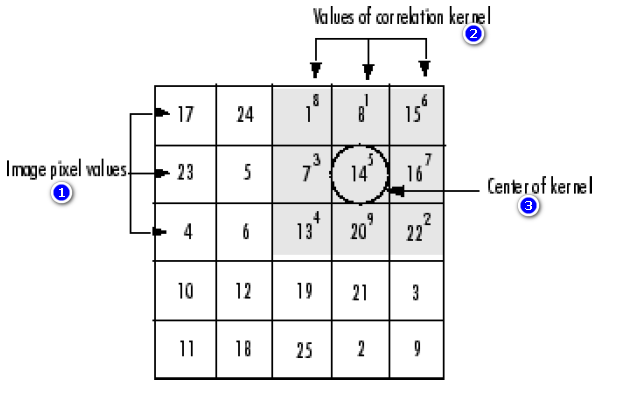
1. درایه ی مرکزی هسته ی همبستگی را بر روی درایه ی $(2,4)$ از ماتریس A قرار دهید.

2. حالا هر یک از عناصر هسته ی همبستگی را در پیکسل های زیرین خود ضرب کنید.

3. حالا اعداد در هم ضرب شده را در گام 2، با یکدیگر جمع کنید.

حالا پیکسل خروجی  همبستگی برابر  است با:

 اعمال فیلترهای خطی بر روی عکس ها با استفاده از imfilter

با استفاده از تابع imfilter می توانید فیلتر درهم پیچیدگی یا همبستگی را بر روی عکس ها اعمال کنید.

در مثال زیر، یک عکس را با استفاده از یک فیلتر 5×5 که حاوی وزن های مساوی است، مورد فیلتر قرار می دهیم. به این نوع فیلترها، فیلتر میانگین(averaging filter) گفته می شود. خودتان این مثال را در متلب امتحان کنید:

مثال(فیلترهای خطی در متلب و پردازش تصویر)

I = imread('coins.png');
h = ones(5,5) / 25;
I2 = imfilter(I,h);
imshow(I), title('Original Image');
figure, imshow(I2), title('Filtered Image')

(شماره 1: عکس اصلی. شماره 2: عکس فیلتر شده)

 بررسی نوع داده ها

نوع داده ها در تابع imfilter درست مشابه با نوع داده ها در توابع محاسباتی عکس ها می باشد. در تابع imfilter، نوع داده ی عکس خروجی، مشابه با نوع داده ی عکس ورودی می باشد. تابع imfilter مقدار هر پیکسل خروجی را با دقت double و بصورت اعداد ممیز شناور(floating-point) محاسبه می کند.

در صورتی که دقت نتیجه ی به دست آمده، از محدوده ی نوع داده بیشتر شود، تابع imfilter حاصل را کوتاه می کند تا در محدوده ی نوع داده ی مجاز خود قرار گیرد. در صورتی که از نوع داده ی integer (اعداد صحیح) استفاده کنیم، تابع imfilter مقادیر کسری به دست آمده را گرد می کند(تا به اعداد صحیح تبدیل شوند).

به دلیل اینکه این توابع عمل کوتاه سازی(truncation) را انجام می دهند، ممکن است شما بخوهید قبل از فراخوانی تابع imfilter عکس خود را به یک نوع داده ی دیگر تبدیل کنید. در مثال زیر، در خروجی تابع imfilter مقادیر منفی یافت می شوند در حالی که عکس ورودی از نوع double می باشد:

مثال(فیلترهای خطی حوزه مکان در پردازش تصویر)

A = magic(5)
A =
17 24 1 8 15
23 5 7 14 16
4 6 13 20 22
10 12 19 21 3
11 18 25 2 9

h = [-1 0 1]
h =
-1 0 1

imfilter(A,h)
ans =
24 -16 -16 14 -8
5 -16 9 9 -14
6 9 14 9 -20
12 9 9 -16 -21
18 14 -16 -16 -2

همان طور که مشاهده می کنید، در خروجی، مقادیر منفی وجود دارند. اکنون فرض کنید که ماتریس A به جای double، از نوع uint8 باشد. بنابراین داریم:

مثال(فیلترهای خطی حوزه مکان در پردازش تصویر)

A = uint8(magic(5));
imfilter(A,h)
ans =
24 0 0 14 0
5 0 9 9 0
6 9 14 9 0
12 9 9 0 0
18 14 0 0 0

 چون که ماتریس ورودی به تابع imfilter از نوع uint8 می باشد، خروجی نیز از نوع uint8 است. و بنابراین مقادیر منفی به 0 تبدیل شده اند(کوتاه شده اند).

 در چنین مواردی، مناسب است که عکس خود را به یک نوع دیگر تبدیل کنیم.

 تنظیمات همبستگی و درهم پیچیدگی

تابع imfilter قادر است تا عمل فیلتر کردن را با استفاده از همبستگی و یا با استفاده از درهم پیچیدگی به انجام برساند.

این تابع به طور پیش فرض، از همبستگی استفاده می کند، زیرا توابع طراحی فیلتر و تابع fspecial ،  هسته های همبستگی را تولید می کنند. اما اگر قصد دارید در فیلتر کردن به جای همبستگی، از درهم پیچیدگی استفاده کنید، می توانید عبارت ‘conv’ را بعنوان یک آرگومان ورودی انتخابی، به تابع imfilter بدهید. بعنوان مثال داریم:

مثال

A = magic(5);
h = [-1 0 1]
imfilter(A,h) % filter using correlation
ans =
24 -16 -16 14 -8
5 -16 9 9 -14
6 9 14 9 -20
12 9 9 -16 -21
18 14 -16 -16 -2
imfilter(A,h,'conv') % filter using convolution
ans =
-24 16 16 -14 8
-5 16 -9 -9 14
-6 -9 -14 -9 20
-12 -9 -9 16 21
-18 -14 16 16 2

تنظیمات پر کردن لبه ها

 هنگامی که می خواهیم مقدار خروجی یک پیکسل که در لبه ی یک عکس قرار دارد را محاسبه کنیم، بخشی از هسته ی درهم پیچیدگی یا بخشی از هسته ی همبستگی، معمولا در خارج از لبه ی عکس قرار می گیرند. این موضوع در عکس زیر نشان داده شده است:

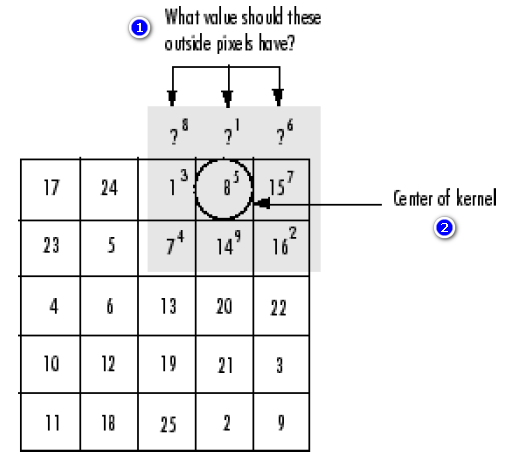
(شماره 1: به این پیکسل های بیرون افتاده، باید چه مقداری بدهیم؟ ؛ شماره 2: مرکز هسته)

تابع imfilter معمولا برای این پیکسل های بیرون افتاده، مقدار 0 را درنظر می گیرد. به این عمل، به اصطلاح zero padding گفته می شود و در تصویر زیر نشان داده شده است:

(شماره 1: پیکسل های بیرونی، 0 در نظر گرفته شده اند. شماره 2: مرکز هسته)

هنگامی که شما یک عکس را فیلتر می کنید، عمل zero padding باعث می شود که لبه های عکس فیلتر شده به رنگ سیاه در بیایند. این موضوع در عکس زیر نشان داده شده است:

مثال

I = imread('eight.tif');
h = ones(5,5) / 25;
I2 = imfilter(I,h);
imshow(I), title('Original Image');
figure, imshow(I2), title('Filtered Image with Black Border')

 (شماره 1: عکس اصلی. شماره 2: عکس فیلتر شده به همراه کادر سیاه رنگ)

 برای از بین بردن آثار  zero-padding که بر روی لبه های عکس، اعمال شده است، تابع imfilter یک روش جایگزین برای پر کردن لبه ها به ما ارائه می دهد که به آن، تکرار شدن لبه ها یا border replication گفته می شود.

در عملِ تکرار شدن لبه ها(border replication)، مقدار هر پیکسل که در خارج از عکس قرار گرفته است، برابر با مقدار پیکسلِ نزدیک ترین لبه در عکس، قرار می گیرد. این موضوع در تصویر زیر نشان داده شده است:

(شماره 1: مقادیر این پیکسل ها برابر با مقادیر لبه ها قرار گرفته است؛ شماره 2: مرکز هسته)

 اگر می خواهید از عمل تکرار شدن لبه ها در فیلتر خوداستفاده کنید، کافیست آرگومان اختیاری replicate را به تابع imfilter بدهید:

مثال(فیلترهای خطی حوزه مکان در پردازش تصویر)

I3 = imfilter(I,h,'replicate');
figure, imshow(I3);
title('Filtered Image with Border Replication')

همان طور که در تصویر بالا مشاهده می کنید، کادر سیاه رنگ دور عکس از بین رفته است.

تابع imfilter از چند خاصیت دیگر نیز در مورد پر کردن لبه ها، پشتیبانی می کند. مثلا از خاصیت circular و symmetric نیز پشتیبانی می کند.

 فیلتر کردن چندبعدی

تابع imfilter قادر است تا عکس های چند بُعدی را مورد استفاده قرار دهد. این تابع همچنین قادر است تا فیلترهای چند بُعدی را اعمال کند. یکی از ویژگی هایی که باعث راحتی کار به هنگام استفاده از فیلترها می شود، این است که اگر بخواهیم یک عکس سه بعدی را به وسیله ی یک فیلتر دو بعدی، مورد فیلتر قرار دهیم، می توانیم هر یک از لایه های عکس سه بعدی را به طور جداگانه با استفاده از همان فیلتر دو بعدی، مورد فیلتر قرار دهیم. مثال زیر، به سادگی روش فیلتر کردن لایه های یک عکس رنگی را با استفاده از یک فیلتر یکسان، نشان می دهد:

1. برای خواندن و نمایش دادن یک عکس رنگی(RGB) دستورات زیر را وارد کنید:

rgb = imread('peppers.png');
imshow(rgb);

2. حالا این عکس را فیلتر می کنیم و سپس نمایش می دهیم:

h = ones(5,5)/25;
rgb2 = imfilter(rgb,h);
figure, imshow(rgb2)

بررسی دیگر توابع فیلتر کردن در متلب

متلب حاوی چندین تابع فیلتر کننده ی دو بعدی و سه بعدی است. مثلا:

• تابع filter2 همبستگی دو بعدی را انجام می دهد.
• تابع conv2 درهم پیچیدگی دو بعدی را انجام می دهد.
• تابع convn درهم پیچیدگی چند بعدی را انجام می دهد.

هر یک از این توابع فیلتر کننده، همواره ورودی خود را به نوع double تبدیل می کند، و بنابراین خروجی آنها همواره از نوع double می باشد.

اما تابع imfilter ورودی خود را به نوع double تبدیل نمی کند.

فیلتر کردن یک عکس با انواع فیلترهای از پیش تعریف شده

تابع fspecial چندین نوع فیلتر از پیش تعریف شده را به شکل هسته های همبستگی، تولید می کند. پس از ایجاد یک فیلتر به وسیله ی تابع fspecial، شما می توانید آن را مستقیما با استفاده از تابع imfilter بر روی عکس خود اعمال کنید.

در مثال زیر، فیلتر unsharp بر روی یک عکس سیاه و سفید، اعمال شده است. فیلتر unsharp باعث می شود که لبه ها و جزئیات دقیق درون عکس بصورت چین و چروک دار(more crisp) نشان داده شوند.

 (عکس سمت چپ: عکس اصلی. عکس سمت راست: عکس فیلتر شده)

منبع