نوامبر 2019

حذف نویز تصاویر با شبکه های عصبی و فیلتر میانی قسمت 1

در عصر مدرن انتقال اطلاعات بصری در فرمت تصاویر دیجیتال به یکی از رایج ترین متدهای اشتراک اطلاعات تبدیل شده است. با این حال تصویر دریافت شده توسط گیرنده ی ارتباط، اغلب آغشته به نویز است. تصویر دریافت شده قبل از هرگونه استفاده ای در یک کاربرد، نیاز به پردازش جهت خذف یا کاهش اثر تخریب کنندگی نویز دارد. علاوه بر این به دلیل نادرست عمل کردن اجزاء سخت افزاری همچنین پیکسل های حسگر دوربین و یا حافظه و یا تبدیل تصویر از یک قالب به قالب دیگر، کپی کردن، اسکن کردن، چاپ و فشرده سازی نیز احتمال افزوده شدن انواع مختلفی از نویز به تصویر وجود دارد. حضور نویز هم از لحاظ ظاهری برای بیننده آزار دهنده است و هم انجام پردازش های بعدی همچون بخش بندی، لبه یابی، تفسیر و تشخیص را با مشکل مواجه می کند. لذا افزایش کیفیت تصویر و حذف نویز موجود در آن یک پیش پردازش اساسی و مهم قبل از هر گونه عملیات دیگر است. کاهش یا حذف نویز به عملیاتی گفته می شود که طی آن پردازش و دست کاری هایی بر روی تصویر ورودی انجام می شود تا تصویر با کیفیت بالاتر جهت استفاده های بعدی به دست آید.

تعیین یک آستامه برای سیستم عصبی برای اینکه سیستم حذف کننده نویز همه پیکسل ها را مورد بررسی قرار ندهد و فقط پیکسل هایی که از این آستانه عبور کنند مورد بررسی و بازیابی قرار گیرند. به همین منظور ابتدا به روش های حذف نویز موجود پرداخته می شود و در انتها این الگوریتم با آستانه مشخص اضافه می شود تا سرعت حذف نویز از تصاویر بیشتر شود.

پردازش تصویر

پردازش تصویر شاخه ای از علم رایانه است که هدف آن پردازش تصاویر برداشته شده توسط دوربین دیجیتال و یا تصاویر اسکن شده توسط اسکنر است. پردازش تصویر از دو جنبه به بهبود اطلاعات بصری برای تفسیر بصری توسط انسان و دیگری ارائه یک تصویر با جزئیات مناسب و کارآمد برای تعبیر توسط ماشین مورد توجه است. (McAndrew, 2004)

سیستمهای پردازش تصویر را می توان در سه سطح پردازشی دسته بندی کرد:

– سطح پایین: عملیات اولیه(مانند حذف نویز، افزایش میزان کنتراست) که در آن ها هم ورودی و هم خروجی سیستم تصویر هستند.

– سطح متوسط: استخراج ویژگی ها (مانند لبه ها، کانتورها، نواحی) از یک تصویر که معمولا این پردازش ها در حیطه بینایی ماشین موجود است.

– سطح بالا: تحلیل و تفسیر محتوایی یک صحنه که اغلب از الگوریتم های یادگیری ماشین در این سطح استفاده می شود.

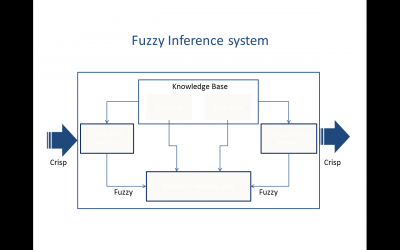
هر سیستم پردازش تصویر معمولا بر حسب نوع کاربرد و هدف نهایی پردازش شامل بخش های مختلفی است. در گام اول یک تصویر توسط یکی از ابزار های تصویر برداری همچون دوربین دیجیتال یا اسکنر بدست می آید. کیفیت تصویر خروجی بلوک تصویر برداری به شدت بر روی کل سیستم تاثیر گذار است. در گام بعد، پیش پردازشی بر روی تصویر ورودی انجام می شود. هدف این پیش پردازش بهبود ظاهری تصویر، بالا بردن کنتراست، حذف نویز، تصحیح درخشندگی، تمیز کردن تصویر یا از بین بردن تاری ناشی از قرار گرفتن سوژه خارج از فاصله کانونی است. در گام بعدی تصویر بر مبنای معیار های مختلفی از جمله ویژگی های بافتی، مولفه های هم بندی، اشکال هندسی و موارد دیگر بخش بندی می شود. و در نهایت در گام نهایی هر یک از بخش ها بر مبنای همین ویژگی ها مورد تجزیه و تحلیل قرار می گیرد و به هر ناحیه یک برچسب نسبت داده می شود. در تمام این مراحل از یک پایگاه دانش بسته به نوع سیستم استفاده می شود. پایگاه دانش علاوه بر محیا کردن دانش لازم برای هر واحد به تعامل بین بخش ها نیز نظارت دارد.(van bemmel and musen, 1997)

پردازش تصویر دارای طیف وسیعی از کاربرد ها است. از آن جمله می توان به موارد زیر اشاره کرد:

– کاربرد های پزشکی

– تفسیر خود کار تصاویر پزشکی سونوگرافی، رادیولوژی و مامو گرافی

– تحلیل تصاویر سلولی از گونه های کروموزوم

– کشاورزی

– پردازش تصاویر ماهواره های جهت تعیین محل مناسب برای کشت محصول

– کنترل کیفیت خود کار محصولات کشاورزی و دسته بندی آن ها در دسته های مختلف

– صنعت

– خودکار سازی خط تولید در کارخانه ها

– تحلیل وضعیت ترافیکی جاده ها

– دسته بندی محصولات کارخانه ای

– قضایی

– تحلیل و بررسی اثر انگشت

– تعیین هویت شخص از روی نشانه های بیومتریک

– تعیین هویت تصاویر(جعلی یا واقعی بودن آن ها)

انواع تصاویر دیجیتال

تصویر در واقع یک تابع دو بعدب مانند (F(x,y است که در آن آرگومان های ورودی x,y مختصات مکانی در هر نقطه به صورت شماره سطر و شماره ستون است. و مقدار تابع شدت روشنایی آن نقطه از تصویر است. از آن جا که مقادیر (F(x,y و x,y مقادیر گسسته اند، تصویر را یک تصویر دیجیتال می نامند. یک تصویر دیجیتال از تعدادی از عناصر با مقدار و موقعیت مشخص تشکیل شده است که به هر یک از این عناصر پیکسل گفته می شود. برای نمایش یک تصویر با ابعاد M*N از یک ماتریس دو بعدی با M سطر و N ستون استفاده می شود. مقدار هر یک از این عناصر این آرایه شدت روشنایی آن پیکسل را نشان می دهد. بسته به نوع داده ای این آرایه دو بعدی، انواع مختلف از تصاویر بوجود می آیند که در ادامه هر یک از انواع تصاویر به طور خلاصه بررسی می شوند.

تصاویر دودویی

در تصاویر دودویی هر کدام از پیکسل ها می توانند یکی از دو مقدار روشن 1 و خاموش 0 را داشته باشند. لذا برای نگهداری هر پیکسل تنها به یک بیت دودویی نیاز است. یکی از اصلی ترین مزایای این گونه تصاویر حجم کم آن ها است و معمولا برای نگهداری نوشته های چاپی و یا دست نویس، اثر انگشت و نقشه های مهندسی از آن استفاده می شود.(Gonzalez and woods, 2005)

تصاویر شدت روشنایی

تصاویر شدت با نام تصاویر خاکستری نیز شناخته می شوند. در این تصاویر مقدار هر یک ار عناصر آرایه دوبعدی تصویر یک عدد 8 بیتی است که می تواند نقداری بین 0 (معادل رنگ مشکی) و 255 (معادل رنگ سفید) را در خود ذخیره کند. دامنه تغییرات عناصر در این گونه تصاویر، اعداد صحیح بین 0 تا 255 است.

تصاویر رنگی

در تصاویر رنگی هر پیکسل دارای یک رنگ مشخص است که خود ترکیبی از سه مولفه رنگی اصلی قرمز، سبز و آبی است و لذا برای ذخیره کردن یک تصویر رنگی با ابعاد M*N نیاز به سه ماتریس با ابعاد M*N است که هر کدام شدت روشنایی هر کدام از مولفه ها را در خود ذخیره می کنند. به عنوان مثال اگر رنگ یک پیکسل قرمز خالص باشد لایه های رنگی آن به صورت [0و0و255] می باشند. برای نمایش سفید خالص هر سه مولفه رنگی برابر 255 و برای مشکی خالص هر سه مولفه برابر صفر است. تصاویر RGB دارای سه لایه رنگی 8 بیتی هستند و لذا بانام تصاویر 24 بیتی نیز شناخته می شوند. این تصاویر سه برابر تصاویر سطح خاکستری هم اندازه خود فضا اشغال می کنند. (Gonzalez and woods, 2005)

تصاویر شاخص

یکی از مهم ترین معایب تصاویر 24 بیتی عدم سازگاری با سخت افزار های قدیمی بود که قادر به نمایش هم زمان 16 میلیون رنگ نبودند. علاوه بر این به حجم بالای ذخیره سازی نیاز داشتند. راه اصلی که همزمان دو مشکل را حل می کند استفاده از یک بازنمایی شاخص دار است که در آن از یک آرایه دوبعدی هم اندازه با تصویر استفاده می شود. لذا برای نمایش هر تصویر شاخص دار از یک آرایه دو بعدی 8 بیتی تصویر و یک نقشه رنگی 256 مدخلی استفاده می شود.

الگوریتم مبتنی بر تصمیم گیری

در (srinirasan and Ebenezer 2007) روشی با نام الگوریتم مبتنی بر تصمصم گیری ارائه شده است. در صورتی که مقدار هر پیکسل بین مینیمم و ماکزیمم مقدار درون پنجره فیلتر قرار گیرد، پیکسل سالم معرفی شده و بدون تغییر باقی می ماند. اگر پیکسل نویزی باشد و مقدار میانه پنجره فیلتر در بازه مینیمم و ماکزیمم پنجره باشد مقدار میانه جایگزین پیکسل خواهد شد و در غیر این صورت مقدار پیکسل با پیکسل همسایه اش جایگزین می شود. الگوریتم DBA در چگالی نویز بالا نیز کارامد است.

متدهای مبتنی بر محاسبات نرم

در سال های اخیر، تکنیک های پیشرفته محاسبات نرم برای عملیات فیلتر گذاری تصاویر با در نظر گرفتن آن به عنوان یک مسئله غیر خطی بکار گرفته شده اند. هم شبکه های عصبی و هم شبکه های با منطق فازی ابزارهای قدرتمندی برای حل طیف وسیعی از مسائل پردازش تصویر هستند. در منبع یک شبمه عصبی نقشه خود سازماندهی برای آشکار سازی پیکسل های نویزی به همراه یک فیلتر تطبیقی برای فیلتر کردن پیکسل نویزی استفاده شده است. شبکه از انحرافات میانه یعنی تفاضل پیکسل های همسایه با میانه پبجره فیلتر به عنوان ورودی استفاده کرده و پیکسل مرکزی را به دو دسته نویزی و سالم طبقه بندی می کند. این فیلتر قابلیت خوبی در حفظ جزئیات تصویر دارد. مهمترین عیب این فیلتر ابعاد بالای ورودی شبکه و انتخاب تصاویر آموزشی است.

در (zvonarev and khryashchev 2005) از ترکیب فیلتر میانه و شبکه عصبی برای بهبود عملکرد حذف نویز استفاده شده است. سیستم پیشنهاد شده، برای جدا سازی پیکسل نویزی از پیکسل سالم از الگوریتم دو مرحله ای استفاده می کند. در تشخیص اولیه، اگر مقدار هر پیکسل درون بازه [min,max] باشد پیکسل سالم و در غیر این صورت نویز تشخیص داده می شود. پیکسل های کاندید برای نویزی بودن به شبکه عصبی فرستاده می شود تا طبقه بندی انجام شود. از ویژگی های محلی آماری برای ورودی شبکه استفاده شده است. مفهوم منطق فازی در سال 1965 توسط آقای زاده به عنوان یک ابزار ریاضی برای مدل سازی عضویت نسبی در مجموعه های معرفی شد. بر خلاف تکنیک های کلاسیک مجموعه ای که تنها عضویت قطعی در آن ها وجود دارد، در منطق فازی امکان تعریف عضویت نسبی وجود دارد.

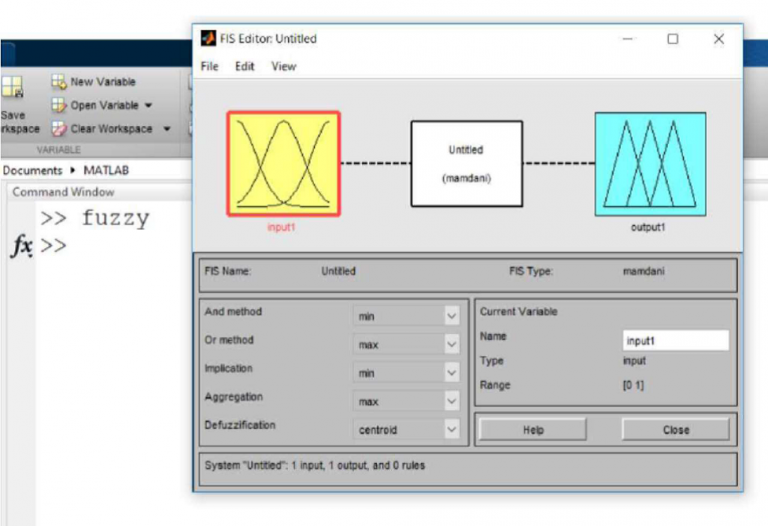
در منبع (yuksel and besdok 2004) از یک سیستم فازی عصبی تطبیقی برای آشکار سازی پیکسل نویزی استفاده شده است که شامل دو زیر آشکار گر مبتنی بر شبکه فازی عصبی با منطق فازی نوع سوگنو است که هر کدام از سه ورودی استفاده می کنند. این سه ورودی پیکسل های عمودی و افقی در یک پنجره 3*3 هستند. هر زیر آشکارگر برای هر ورودی سه تابع و سه تابع زنگوله ای برای هر ورودی، 27 قاعده برای تصمیم گیری است.که وزن ها بر اساس شدت آتش هر قاعده تعیین می شود. در نهایت میانگین خروجی دو زیر آشکارگر محاسبه می شود و از یک آستانه نهایی برای تشخیص پیکسل نویزی استفاده می شود.

در فیلتر های حذف نویز، طبقه بندی هر پیکسل با برچسب نویزی یا سالم معمولا از طریق مشاهدات همسایگی پیکسل انجام می شود. یک راه ساده برای طبقه بندی اندازه گیری میزان اختلاف پیکسل مرکزی و خروجی فیلتر میانه است. در صورتی که میزان اختلاف از یک حد آستانه بیشتر باشد، پیکسل به عنوان پیکسل نویزی و در غیر این صورت پیکسل به عنوان سالم بر چسب می خورد. این راه حل در نگاه اول ساده به نظر می رسد، اما تعیین مقدار مناسب آستانه بحث بر انگیز است و تعیین چنین آستانه هایی معمولا امری مشکل است. در یک رویکرد فازی، با استفاده از شروط فازی و توابع عضویت، میزان نویزی بودن هر پیکسل تعیین می شود و می توان از این طبقه بندی هم در بخش طبقه بندی اولیه در سیستم حذف نویز و هم در تخمین مقدار نهایی برای پیکسل نویزی استفاده کرد.

در قسمت های قبل مفاهیم پایه و انواع تصاویر و همچنین مدل های مختلف نویز بررسی شد و تاثیر هر کدام از انواع نویز بر روی تصاویر سطح خاکستری نشان داده شد. هر کدام از انواع نویز تاثیر متفاوتی بر روی کیفیت تصویر اصلی می گذارند و بر همین اساس از رویکرد های متفائتی برای کاهش اثر هر کدام از انواع نویز استفاده می شود. متد های فوق و پایه ای در حذف نویز ضربه در این قسمت مرور شد. در ادامه متدی برای کاهش اثر نویز ضربه بر روی تصاویر دیجیتال بررسی می شود.

نوامبر 30, 2019/0 دیدگاه /توسط daliri

نویز چیست؟ قسمت 2

آموزش عمومی پردازش تصویر و بینایی ماشین

نویز چیست ؟

نویز Noise در معنای لغوی به معنی سر و صدا می باشد اما در عمل به انرژی نامطلوب و ناخواسته ای گفته می شود که کم ترین سطح سیگنالی را که یک مدار می تواند آن را با کیفیت قابل قبول پردازش کند ، محدود می کند. چرا که اگر سطح سیگنال از یک آستانه ای کمتر شود و نسبت سیگنال به نویز یا SNR ( مخفف Signal to Noise Ratio ) به عدد 1 نزدیکتر شود باعث مخلوط شدن سیگنال نویز و سیگنال اصلی شده و حذف کلی سیگنال اصلی را منجر می گردد. امروزه طراحان آنالوگ پیوسته درگیر مساله نویز هستند زیرا با مساله اتلاف توان ، سرعت و میزان خطی بودن مدار در ارتباط است. اکثر منابع نویز در مدارها توان متوسط ثابتی دارند.

طیف نویز

مفهوم توان متوسط اگر با در نظر گرفتن محتوای فرکانسی نویز تعریف شود ، پیچیده تر می شود. نویز صوتی که توسط یک گروه از مردان تولید می شود شامل مولفه های فرکانس بالای ضعیف تری نسبت به نویز صدای گروهی از زنان است و این تفاوت در طیف هر نوعی از نویز قابل مشاهده است. طیف نویز که آن را چگالی طیفی توان نویز یا PSD نیز می نامند ، نشان می دهد که سیگنال ، چقدر توان در هر فرکانس حمل می کند. به طور خاص ٬ PSD یا (Sx(f1 به صورت توان متوسطی که نویز (X(t در یک هرتز پهنای باند اطراف f حمل می کند ، تعریف می شود. همانطور که در شکل (الف) رسم شده است ، ( X(t را به فیلتر میان گذر با فرکانس مرکزی f1 و یک هرتز پهنای باند حول آن ، اعمال می کنیم. سپس خروجی را به توان ۲ رسانده و متوسط آن را روی یک مدت طولانی برای یافتن (Sx(f1 حساب می کنیم. با تکرار این فرآیند به وسیله فیلتر های میان گذری که فرکانس مرکزی متفاوتی دارند شکل کلی (Sx(f شکل (ب) را بدست می آوریم.

قضیه : اگر یک سیگنال با طیف (Sx(f به یک سیستم خطی غیر متغیر با زمان که تابع تبدیل آن (H(s است وارد شود ٬ طیف خروجی آن برابر است با:

Sy(f)=Sx(f).|H(f)|^2

این قضیه با انتظار منطقی ما از اینکه طیف سیگنال باید توسط تابع تبدیل سیستم (شکل بالا) تغییر شکل یابد٬ سازگار است. برای مثال همانطور که در شکل زیر رسم شده ٬ چون تلفن های معمولی تقریبا پهنای باند ۴KHz دارند ٬ مولفه های فرکانس بالای صدای گوینده ٬ را حذف می کنند. توجه کنید که به دلیل محدودیت پهنای باند ٬ (Xout(t تغییرات آهسته تری نسبت به( Xin(t دارد.

انواع نویز

سیگنال های آنالوگ که با مدارهای مجتمع پردازش می شوند توسط دو نوع مختلف از نویز مغشوش می گردند:

۱-نویز ناشی از ادوات الکترونیکی

۲- نویز محیطی

نویز محیطی اغتشاشی ظاهرا تصادفی است که مدار از طریق خط تغذیه یا زمین و یا از طریق بنا بدان دچار می شود. در اینجا روی نویز ادوات الکترونیکی تمرکز می کنیم.

نویز حرارتی

نویز حرارتی مقاومت: حرکت تصادفی الکترون ها در یک رسانا باعث افت و خیز هایی در ولتاژ اندازه گیری شده روی آن می شود حتی اگر جریان متوسط صفر باشد. بنابراین طیف نویز حرارتی با دمای مطلق متناسب است. همانطور که در شکل زیر نشان داده شده است ٬ نویز حرارتی یک مقاومت R را می توان با یک منبع ولتاژ سری مدل کرد که چگالی طیفی یک طرفه آن برابر است با: Sv(f)=4kTR , 0≤f که k ثابت بولتزمن می باشد.

نویز حرارتی ماسفت ها: ترانزیستورهای MOS نیز نویز حرارتی تولید می کنند. مهم ترین منبع نویزی است که در کانال تولید می شود. می توان ثابت کرد که برای ادوات MOS با کانال بلند٬ که در اشباع کار می کنند٬ نویز را می توان با یک منبع جریان که بین ترمینال های درین و سورس وصل شده مدل کرد (شکل زیر) که چگالی طیفی آن عبارت است از:

ضریب γ (لاندا) با ضریب اثر بدنه اشتباه نشود γ برای ترانزیستورهای کانال بلند برابر با ۲/۳ است و برای ماسفت های زیرمیکرون لازم است که آن را با مقادیر بزرگتری جایگزین کرد.

نویز فلیکر

مرز بین اکسید گیت و زیربنای سیلیکن در ماسفت خواص جالبی دارد. چون کریستال سیلیکن در این مرز تمام می شود٬ تعداد بسیاری پیوند آویزان به وجود می آید٬ که حالت های انرژی اضافه تولید می کنند(شکل زیر). وقتی که حامل های بار در این مرز حرکت می کنند٬ بعضی از آنها به طور تصادفی بدام می افتند و دوباره آزاد می شوند و باعث ایجاد نویز فلیکر در جریان درین می شوند. اعتقاد بر این است که چند ساز و کار دیگر نیز علاوه بر بدام افتادن الکترون ها در تولید نویز فلیکر موثرند.بر خلاف نویز حرارتی ٬ توان متوسط نویز فلیکر را نمی توان به آسانی پیش گویی کرد.بسته به تمیزی مرز اکسید-سیلیکن ٬ نویز فلیکر مقادیر متفاوتی را خواهد داشت و از یک فناوری CMOS به نوع دیگر تغییر می کند. نویز فلیکر به آسانی با یک منبع ولتاژ که با گیت سری است مدل می کنند و تقریبا برابر است با :

منبع

نویز چیست ؟

نویز در لغت به معنی “صدا” می‌باشد، صدایی که دارای هیچ وزن موسیقی نیست و به طور نامنظم است. اما به طور کلی نویز سیگنالی است ناخواسته که بر روی دستگاه الکترونیکی یا الکتریکی ما تاثیر می‌گذارد و به سه دسته زیر تقسیم می‌شود:

Background Noise (نویز زمینه)
Modulated Noise (نویز نوسانی)
Interference Noise (نویز مزاحم)

بحث ما در مورد گزینه دوم یعنی نویز نوسانی می‌باشد به طوری که سیگنال سالم ما را پوشش می‌دهد و باعث بهم ریختگی سیگنال ما می‌شود.

نویز در دوربین‌های مداربسته

اگر در منزل یا محل کار خود از دوربین مداربسته استفاده می‌کنید و با مشکل در دریافت خروجی تصویر به صورت غیر واضح یا رنگ پریدگی تصویر مواجه شدید حتما نویز مزاحم دارید. به شکل زیر توجه کنید:

حال با توجه به اینکه دوربین مداربسته شما آنالوگ است یا دیجیتال تاثیرات نویز را روی سیگنال خروجی می‌بینید. با نویز تا حدودی آشنا شدیم حال چه کنیم که کمترین آسیب را از نویز در دوربین های مداربسته داشته باشیم:

از سالم بودن قطعات الکتریکی مطمئن شویم.
سالم بودن کابل‌ها و کیفیت خوب آن‌ها.
مسافت کابل‌ها بیش تر از ظرفیت انتقال سیگنال‌های آن کابل نباشد، به عنوان مثال در بعضی از کابل‌ها ابتدا و انتهای اتصال کابل نمی‌تواند بیشتر از ۱۰ یا ۲۰ متر باشد و کابل پهنای باند لازم برای انتقال سیگنال را ندارد.
مسیر کابل کشی کنار کابل و سیم‌های دیگر نباشد.
دستگاه‌های ورودی مانند دوربین و دستگاه خروجی مانند DVR در کنار قطعات و کابل‌های الکتریکی نباشند.
حتما در مسیر کابل کشی‌ها از داکت یا ترانک استفاده شود تا از حداقل تاثیرات نویز نیز کاسته شود.

منبع

نویز چیست؟ قسمت 1

نویز چیست؟ قسمت 2

نوامبر 29, 2019/0 دیدگاه /توسط hgadmin

نویز چیست؟ قسمت 1

آموزش عمومی پردازش تصویر و بینایی ماشین

نوفه یا «نویز» (به انگلیسی: Noise) بمعنای آلودگی صوتی یا نشانکی (سیگنال) ناخواسته است که شکل نشانک‌ها را تغییر می‌دهد و باعث بروز اختلال می‌شود.

پژوهشگران ناسا در «مرکز پژوهش گلِن» بر سر اجرای آزمون‌های نوفهٔ موتور هوانورد در ۱۹۶۷م

نوفه در اندازه‌گیری مقدارهای خروجی یک سامانه تأثیر می‌گذارد چنان‌که مقدار مثبوت آن با مقدار واقعی آن فرق دارد. اگر مقدارهای شمارش حاصل از یک منبع پرتوزا را پی در پی اندازه بگیریم، می‌توانیم مقدار شمارش متوسّط را محاسبه کنیم و سپس انحراف معیار را بدست آوریم. در این حالت، اندازه‌گیری‌های چندگانه برای بهبود دقّت اندازه‌گیری و تعیین دقیق‌تر مقدار متوسّط انجام می‌شوند و نوسان‌های زیاد در اندازه‌گیری نشانگر نوفهٔ سامانه است. این نوسان‌ها ذاتاً تصادفی می‌باشند و با تعیین انحراف معیار (σ) ارزیابی می‌شوند.

نوفهٔ روی یک تصویر، اغلب دارای اجزای بسامدی (فرکانسی) نیز می‌باشند و واکاوی بسامدی شبیه به نشانک (اطّلاعات واقعی تصویر) دارد. بیناب توان نوفه که «بیناب وینِر» هم نامیده می‌شود همان وردایی (واریانس) نوفه ۲(σ) تصویر است که بصورت تابعی از بسامد فضایی (f) بیان می‌گردد.

نویز در شبکه‌های رایانه‌ای

در شبکه‌های رایانه‌ای حرارت، القا و هم‌شنوایی سبب ایجاد نوفه می‌شوند.

حرارت

حرارت باعث می‌شود الکترون‌ها در جهت‌های نامشخّص آغاز به حرکت کنند، این حرکت گاهی با نشانک‌ها هم‌جهت می‌شوند و اندازه و شکل آنها که همان الگوهای نشانک‌هاست را تغییر می‌دهد و نوفه پدید می‌آید.

القای الکترومغناطیسی

موتورهای مکانیکی مانند موتور خودرو یا موتورهای الکتریکی وسیله‌های خانگی نوفهٔ القایی می‌آفرینند. این وسیله‌ها مانند یک آنتن فرستنده کار می‌کنند و می‌توانند نوفه را ارسال کنند و بافهٔ شبکه، مانند یک آنتن گیرنده نوفه‌های ارسالی را دریافت می‌کند. بافه‌های برق فشار قوی یا رعد و برق نیز نوفهٔ القایی ایجاد می‌کنند.

هم‌شنوایی

هم‌شنوایی اثر میدان‌های مغناطیسی یک بافه کنار خود است.

منبع

در زندگی روزانه نویز(noise) به صدایی ناخواسته و بلند گفته می‌شود که هیچ نظم موسیقی نداشته باشد در دورانی که ارتباط رادیودیی وجود داشت ، نویز “هر سیگنال الکتریکی که باعث مختل کردن ارتباط رادیودیی می‌شود ” تغریف شد . ( برگرفته از فرهنگ لغت وبستر). این نوع نویز قبل شنیدن بود ؛ مانند نویزی که در گوشی‌ها می‌شنویم .

در یک تعریف کلی تر ، به هر نوسان و تغییر غیر عمدی که بر روی سیگنال‌های مورد اندازه گیری ظاهر می‌شود ،نویز گفته می‌شود . هر کمیتی می‌تواند نویز بپذیزذ . در مدار‌های الکتریکی ما با نویر ولتاژ و نویز جریان یر و کار داریم ؛ این نویز ناشی از تغیرات گرمایی و تاثیر آنها بر روی حامل‌های الکترونیکی است . در ناحیه رادیو و میکرو ویو ما با نویز‌های الکترو مغناطیسی سر و کار داریم . نویز‌هایی که ناشی از گرما یا تابش وتون‌های کم انرژی است . ولی نویز می‌تواند به تغییرات غیر عمدی کمیت‌های دیگری نیز باشد . مانند ترافیک در اتوبان‌ها( مثال بارزش اتوبان‌های تهران که اصلا همش نویز هست!)یا ریتم قطره‌های ا بر روی سقف .
نویز در همه جا حضور دارد ؛ هرجا که کسی سیگنالی را بخواهد اندازه گیری کند ، حتما یک نوع نویز بر روی آن می‌افتد . هر آزمایش دقیق و با کیفیت بالا که در دنیای فیزیک انجام می‌ود ، به کار زیادی نیاز دارد تا بتوان نویز محیط را پیش بینی و همچنین به طرقی تاثیر آن را کم کرد. اهمیت تحلیل نویز وقتی کاملا نمایان می‌شود که یک فرد متوجه بشود که کیفیت سیگنا انازه گیری شده به وسیله ی مقدار مطلق انرژی سیگنال تعیین نمی‌شود بلکه از نسبت سیگنال به نویز تعینن میشود . نتیجه تحققات نشان می‌دهد که بهترین روش برای بهبودی نسبت سیگنال به نویز ، کاعش نویز است نه افزایش قدارت سیگنال .
نویز تصادفی طبق تعریف ، غر قابل کنترل است و مقدار دقیق آن در آزمایش‌های مختلف با هم فرق دارد. پس بهتر است که به صورت آماری نشان داده شود .
نویز تصادفی است و معمولا توزیع آن را توزیع گاوسی در نظر می‌گیرند( البته این توزیع معمولا در نظر گرفته می‌شود ولی در شرایط متفاوت ممکن است توزیع‌های متفاوتی در نظر گرفته شوند ) . تصادفی بودن نویز باعث می‌شود که میانگین آن صفر شود . پس برای توصیف آن از مقادیر توان دو آن استفاده می‌شود . مقدار موثر نویز از جذر میانگین مربعات آن بدست می‌آید .(rms) .البته این پارامتر هیچ اطلاعاتی در مورد نتغیر با زمان بودن نویز و یا اجزای فرکانسی آن نمی‌دهد .
لازم است تغییر پذیری با زمان را برای نویز تعریف کنیم . نویزی را ایستا می‌گوییم ( نا متغیر با زمان ) که ویژگی‌های آماری آن با زمان تغییرنکند. به طور مثال واریانس و یا مقدار موثر آن با زمان تغییر نکند .

در سیستم‌هایی که چند منبع نویز وجود داشته باشد نویز کلی می‌تواند به صورت مجموع نویز‌های مختلف نوشته شود . اگر این نویز‌ها مستقل از یکدیگر باشند می‌توان مقدار موثر را به صورت جمع مقدار‌های موثر تک تک منابع نویز نوشت . ( نویز‌هایی مستقل هستند که میانگین حاصلضزب دو به دوی نویز‌ها صفر شود )

انواع نویز :

نویز بر اساس تغییرات زمانی و فرکانسی خود بیشتر مشخص می‌شوند . در شکل زیر نویز را بر اساس چگالی طیفی نویز ( که بر اساس فرکانس است) رسم شده است.
نویز‌هایی که در زیر آمده است ، معمول ترین نویز‌های موجود هستند :
۱-   نویز سفید طیفی (یا در واقعیت ، نویز صورتی)
۲-   آشفتگی های هارمونیک
۳-   نویز ۱/f
4-   رانش

در اینجا ، منبع هر کدام از نویز‌ها مورد بررسی قرار می‌گیرد و مهمترین نویز ، نویز سفید ، بیشتر تاکید می‌شود .
1- نویز سفید: طیفی طبق تعریف به نویزی گفته می‌شود که طیف چگالی آن به فرکانسی بستگی نداشته باشد .( مقدار ثابتی باشد ). البته این یک تعریف ایده ال است چون اگر از یک عدد ثابت نسبت به فرکانس انتگرال بگیریم ، واریانس نویز ( یا همان انرژی نویز ) بی نهایت به دست می‌آید . در سیستم‌های‌هایی که بیشتر مورد بررسی قرار می‌گیرند ، نویز عملا سفید نیست بلکه “صورتی ” است .به این معنا که داری فرکنس قطع می‌باشد . این فرکانس قطع باعث می‌شود که واریانس نویز محدود شود . در سیستم‌های کاربردی ، به اندازه ی کافی بزرگ است و مقدار چگالی طیفی آن به اندازه ی کافی ثابت است تا مدل نویز سفید را راضی کند . نویز سفید طیفی یکی از بنیادی ترین و فیزیکی ترین نویز‌ها در لیست بالا است .
بیشتر نویز‌های فوق را می‌توان ( به طور کلی) با استفاده از طراحی‌های زیرکانه برداشت ولی محدودیت‌های بنیادی نویز سفید آن را محدود می‌کند. نویز سفید به دو صورت ظاهر می‌شود : نویز دمایی و اثر ساچمه ای .
2- آشفتگی‌های‌هارمونیکی: واقعا نویز‌های تصادفی نیستند بلکه آشفتگی هایی هستند که از منابع نزدیک گرفته میشود (یا اصطلاحا نویز از طریق منابع نزدیک روی سیستم افتاده است). این نویز‌ها می‌توانند به وسیله ی طراحی‌های مناسب حذف بشوند. ترفند‌های که برای حذف این نویز استفاده می‌شوند عبارتند از : پوشش، زمین کردن مناسب ، کاهش حساسیت سیستم به نویز گرفتن .از آنجایی که آشفتگی‌های هارمونیکی دارای فرکانس‌های مشخصی هستند، باعث ایجاد نوسانات غیر میرا در سیگنال و ایجاد ضربه در طیف فرکانسی می‌شوند. این رفتار تکین باعث میشود که نوع آنها با نویز‌های دیگر فرق کند.( توی آزمایشگاه‌های الکتریسیته، می توان نویز برق شهر را بر روی اسیلوسکوپ مشاهده کرد. فقط کافی است دو دست خود را به ورودی‌های اسکوپ وصل کنید ؛ چون بدن مثل آنتن عمل میکند و این نویز را که در فضا پر است را می‌گیرد.)
3- نویز ۱/f : از روی اسم نویز ۱/f می‌توان فهمید که رفتار آن چگونه می‌تواند باشد .چگالی طیفی این نویز با آهنگ ۱/f کاهش پیدا می‌کتد. این نویز در وسایل نیمه رسانا حضور دارد و عموماً به ” دام‌های ژرف (deep traps) ” نسبت داده می‌شود ؛ این دام‌های ژرف باعث می‌شوند که حامل‌ها برای مدتی به دام بیفتند. البته مکانیزم ایجاد این نویز همیشه مشخص نیست. در نتیجه ی این دام‌های ژرف و کند، ویژگی‌های وسیله با زمان به صورت کندی تغییر می کنند و این کندی تغییر یعنی در فرکانس‌های پایین این نویز دارای بیشترین انرژی می‌باشد. قدرت نویز ۱/f بستگی به نحوه ی تولید دارد از وسیله ی به وسیله ی دیگر متفاوت است. برای یک وسیله ی نیمه‌هادی، جایی که قدرت نویز ۱/f با نویز سفید برابر می‌شود در یک بازه ی بزرگ ۱ هرتز تا ۱۰۰ کیلو هرتز است .
4- رانش: کمی‌ قبلتر گفتیم که نویز بدون هیچ مقدار ثابتی است یعنی مقدار میانگین آن صفر است. _N(t)_ = 0. ولی باید گفت که این جمله همیشه درست نیست . در بعضی سیستم‌ها مقدار ثابت نمودار با زمان تغییر میکند(برای دوستانی که با تبدیل و سری فوریه آشنایی ندارند باید توضیح بدهم که در بسط دادن یک سیگنال به صورت سینوسی و یا نمایی ، مقداری ظاهر می‌شود که آن مقدار ثابت منحنی می‌گویند. این مقدار ثابت نشان دهنده ی میانگین نمودار است و می‌توان برای شکلهای متقارن گفت که نمودار روی آن سوار می‌شود. مثال: یک موج سینوسی که به جای حرکت رو ی محور x ‌ها روی مقدار y=1 حرکت می کند). وقتی که این مقادیر ثابت به صورت خطی و ثابت تغییر می کنند، به آن رانش گفته می شود .البته این جمله ممکن است کمی‌بی معنا باشد ولی می‌توان گفت که این نویز دارای فرکانس بسیار پایین است؛ چون تبدیل فوریه یک تابع با شیب ثابت یک چیزی شبیه مشتق تابع ضربه در اطراف صفر است. بهتر است واژه ی رانش برای نویز‌هایی گفته شود که در طول زمان دارای تغییرات خطی هستند چون در صورت بروز تغییرات تبدیل فوریه ی آن دارای فرکانس‌هایی خواهد بود که غیر از فرکانس صفر است .

در اینجا به عوامل ایجاد کننده ی نویز‌های مختلف اشاره می‌کنیم:

نویز دمایی :

همانطور که گفته شد نویز سفید ، بنیادیترین نویز است و لی این حرف باید کامل شود؛ نویز سفید با منشأ دمایی این ویژگی را دارد. نویز دمایی که بعضی اوقات نویز جانسون هم گفته می شود یک نتیجه ی طبیعی از نظریه ی نوسان-اتلاف است. این نظریه بیان می‌کند که هر المان اتلاف کننده انرژی نوساناتی خود به خود متناسب با قدرت اتلاف المان هنگامی‌که تحت یک میدان خارجی است، ایجاد می‌کند.(یک ذره نامفهوم هست، نه؟). منشأ فیزیکی نوسانات و اتلاف کوپلاژ و اتصال بین المان و محیط اطراف است. یک اتصال قوی باعث ایجاد اتلاف زیاد و در نتیجه نوسانات زیادی می‌شود. در فرکانس‌هایی کمتر از f << kT/h, که در آن k ثابت بولتزمن، h ثابت پلانک و T دمای محیط است. مقدار انرژی طیفی نوسانات دمایی ثابت و مقدار آن متناسب با دما است. به همین خاطر به آن نویز سفید دمایی گفته میشود(چون مقدار ثابتی دارد).
یک مثال از نویز دمایی نوسانات ولتاژ در مقاومت است. در حضور یک میدان خارجی مقدار اتلافی که وجود دارد برابر با V^2/R است. وقتی که میدان خارجی وجود نداشته باشد و همان اتم‌ها و الکترون‌هایی که در حضور میدان باعث ایجاد گرما می‌شدند، با هم برخورد می‌کنند ولی این بار یک ولتاژ بین دو سر اتصال مقاومت ایجاد می‌کنند(به دلیل تغییرات در چگال الکترون‌ها در دو طرف مقاومت). واریانس این تغییرات ولتاژ برابر است با : ۴kTRΔf که با تقسیم کردن آن بر فرکانس چگالی طیفی نویز به دست می‌آید. در دمای اتاق ، برای یک مقاومت ۱k در یک پهنای باند یک مگاهرتر تغییرات ولتاژ ۰٫۹ میکرو ولت بدست می‌آید . یعنی می‌توان گفت که تغییرات ولتاژ در حد ۱ میکرو ولت خواهد بود .

نویز یا اثر ساچمه ای (Shot noise)

اثر ساچمه ای زمانی اتفاق می‌افتد که یک سری المان‌های گسسته از یک مانع به صورت غیر مستقل عبور می‌کنند. مدل اثر ساچمه ای، جریان آبی است که در اثر برخورد باران با سقف بوجود می‌آید . باران شامل قطراتی است که کم و بیش به صورت مستقل برخورد می‌کنند . این قطرات در جریان آب به صورت بی قاعده اثر می‌گذارند و مقدار آن را در لحظاتی زیاد می‌کنند . قطرات، یا بهتر از ان تگرگ، در هنگام برخورد با سقف صدا ایجاد می‌کنند. این صدا همان اثر ساچمه ای یا Shot noise است. مثال‌های دیگری از اثر ساچمه ای عبارتند از : الف) تغییرات در جریان الکتریکی تولید شده توسط الکترون‌ها از کاتد و ب) تغییرات در شار نوری تولید شده توسط فوتون‌ها در هنگام بر خورد با یک ماده ی حساس به نور.

در زیر نشان می‌دهیم که نوسانات ایجاد شده توسط اثر ساچمه ای در تمام فرکانس‌ها پخش می‌شود(البته تا یک فرکانس قطع معین). این فرکانس قطع، با عکس زمان تداوم هر کدام از برخورد‌ها را بطه ی مستقیم دارد؛ به عبارت دیگر، اثر ساچمه ای از نظر طیفی سفید است، همانطور که نویز گرمایی هم سفید است. در یک جریان الکتریکی ، نویز ساچمه ای از رابطه ی زیر بدست می‌آید :

Si(f) = 2qi0 [A2/Hz]

که در آن i0 مقدار میانگین جریان است q هم بار یک الکترون است .
یک مطلب دیگر در مورد نویز ساچمه ای این است که هر المان (کوانتا) به صورت نا همبسته(uncorrelatd) وارد می‌شود. هنگامی که همبستگی رخ می‌دهد، مقدار نویز (طبق قاعده) از مقدار حدی نویز ساچمه ای پایین می‌آید. به عنوان مثال در یک مقاومت، نوسانات موجود در جریان به دلیل همبستگی بار‌های حامل بوجود می‌آید(همدیگر را لمس می‌کنند) . مقاومت از خود نویز ساچمه ای نشان نمی‌دهند. نمونه‌های دیگری از نویز ساچمه ای که دارای همبستگی می‌تواند باشد : الف) نوسان در جریان کاتدی به دلیل وجود بار‌های موجود در فضا است ب) تغییرات در شدت لیزر‌ها هنگامی که لیزر در منطقه ای بیشتر از آستانه ی خود کار می‌کند .

نویز ۱/f (نویز صورتی)

همه ی سیستم‌ها دارای نویز سفید می‌باشند. ولی بعضی سیستم‌های کاربردی علاوه بر آن نویز توسط نویز‌هایی با فرکانس پایین نیز آلوده شده اند. وقتی که این نویز طوری باشد که با شد که مقدار انرژی طیفی آن با نرخ ۱/f کاهش پیدا بکند، گوییم که نوع نویز ۱/f است (نویز صورتی). اهمیت نویز ۱/f در فرکانسی به نام فرکانس گذار مشخص می‌شود : در فرکانس‌های زیر این فرکانس نویز صورتی و در فرکانس های بالای این فرکانس نویز سفید غالب است.
نویز ۱/f می تواند در آزمایشات خیلی مزاحم باشد. در مواد نیمه‌هادی، منشاء این نویز‌ها، ناخالصی‌هایی است که در هنگام ساخت وارد ماده می‌شود( نه آن ناخالصی که باعث ایجاد n و P می‌شود). این ناخالصی‌ها بیشتر بر روی سطح نیمه‌هادی رخ می‌دهد تا درون آنها به همین دلیل موادی که دارای سطوح زیادی هستند، بیشتر از این نویز رنج می‌برند(مثل MOSFET‌ها). با پیشرفت تکنولوژی این نویز ممکن است آن قدر کم شود به طوری که بتوان از آن صرف نظر کرد.

معرفی EMG:

جریانهای الکتریکی کوچکی هستند که توسط فیبر‌های عضلانی به منظور فراهم کردن نیروی لازم عضلانی تولید می‌شوند. این جریانات به وسیله تبادلات یونی که در سطوح فیبر‌های ماهیچه ای صورت می‌گیرد تولید می‌شوند. این سیگنال‌ها که الکترومیوگرام (EMG) نامیده می‌شوند را می‌توان ازطریق قرار دادن المان‌های رسانا یا الکترود‌ها بر روی سطح پوست و یا به طور تهاجمی‌ از طریق قرار دادن در داخل فیبر ماهیچه ای اندازه گیری کرد.
اندازه گیری EMG به صورت سطحی از روی پوست به تعدادی از عوامل و دامنه سیگنال سطحی (sEMG)- که در رنج میکروولت تا چند میلی ولت تغییرات دارد – بستگی دارد .دامنه و فرکانس مشخصه سیگنال‌های EMG را می‌توان به عوامل زیر مرتبط دانست :
•   مدت زمان وقدرت انقباضی ماهیچه‌ها
•   فاصله الکترود‌های ماهیچه‌های فعال
•   مشخصه و خاصیت بافت‌های سطحی
•   جنس و مشخصه الکترود‌ها
•   اتصال مناسب بین الکترود و پوست
در اکثر موارد اطلاعاتی که در مورد مدت زمان و قدرت انقباض عضله می‌باشند بسیار مطلوب هستند. بقیه عوامل مانده فقط موجب نامطلوب تر شدن تغییرات در در ثبت EMG می‌شوند و موجب می‌شوند که تجزیه و تحلیل نتایج بسیار دشوار گردد. با وجود این روش‌هایی وجود دارد اثرات آن عوامل غیر عضله ای که بر روی سیگنال EMG تغییرات ایجاد می‌کنند کاهش داد:
•   استفاده از الکترود‌ها و تقویت کننده‌های همسان (به طور مثال اصلاح مشخصه‌های اطلاعات در پارامتر‌های سیگنال در خط انتقال از طریق تصحیح خصوصیات فاز و دامنه تقویت کننده‌ها )
•   اطمینان از همنواختی اتصال بین الکترودها و پوست
از این طریق می‌تواند با جابجایی پی در پی الکترود‌های در نواحی مختلف پوست میزان تغییرات ناخواسته در رنج EMG را کاهش داد. علاوه بر این از روش‌هایی برای نرمالیزه کردن سیگنال EMG در درون و بین الکترود‌ها و عضله استفاده کرد. تعداد بسیار زیادی از اطلاعات مهم مرتبط با ثبت و فراگیری و آنالیز سیگنال‌های sEMG را می‌توانید از طریق رفت به آدرس زیر کسب کنید :

(www.rrd.nl/projects/content/file_100.html) (Freriks and Hermens, 2000)

اندازه گیری و نتایج درست تا حد زیادی به مشخصه ی الکترود‌ها و تعامل متقابل آن با پوست – نوع طراحی تقویت کننده و تبدیل سیگنال‌ها از آنالوگ به دیجیتال (A/D ) وابسته است. کیفیت سیگنال EMG اندازه گیری شده به طور معمول به صورت نسبت سیگنال ثبت شده به نویز ناخواسته از محیط بیان می‌شود. هدف افزایش دامنه و متقابلاً کمتر کردن مقدار نویز وارده است.

منبع

نوامبر 28, 2019/0 دیدگاه /توسط daliri

سیستم استنتاج فازی چیست؟ قسمت 2

آموزش های عمومی هوش مصنوعی

سیستم استنتاج فازی (Fuzzy Inference Systems (FIS

قوانین اگر- سپس Fuzzy از فرم IF A THEN B هستند که A و B علامت مجموعه های فازی هستند.

ممداني، سوگنو، لارسن و تاكاگی

ممداني: متغييرهاي ورودي در اين روش فازي و خروجي هم فازي مي‌باشد.

سوگنو: مانند ممداني ولي ورودي ها فازي ولي خروجي مي‌تواند فازي نباشد.

تاكاگي: مانند ممداني ولي در خروجي از ميانگين وزني استفاده مي‌شود.

لارسن: تفاوت مهم آن با روش‌هاي قبلي در متغييرهاي ورودي هستند كه مي‌تواند هم فازي و هم غير فازي باشد.

انواع سیستم های استنتاج فازی (1) (ممدانی)

سیستم های فازی خالص

انواع سیستم های استنتاج فازی (2)

سیستم های فازی تاکاگی – سوگنو و کانگ (TSK)
یک میانگین وزنی از مقادیر بخش هاي آنگاه قواعد می باشد.
قسمت مقدم قواعد، فازی اما قسمت نتیجه، غیرفازی و ترکیبی خطی از متغیرهای ورودی است.

Sugeno model

Assume that the fuzzy inference system has two inputs x and y and one output z.

A first-order Sugeno fuzzy model has rules as the following:

Rule1:

If x1 is A11 and x2 is A21, then y = p1x1 + q1x2 + r1

Rule2:

If x1 is A12 and x2 is A22, then y = p2x1 + q2x2 + r2

مدل Sugeno

تکنیک های استنتاج فازی

گریزی بر شبکه های عصبی

شبکه های عصبی یک مدل محاسباتی از عملیاتی است که در مغز انسان صورت می گیرد . شبکه های عصبی از تعدادی گره تشکیل شده است که توسط ارتباطاتی به هم متصل می باشند.

هر ارتباط یک وزن عددی مختص به خود دارد.

وزن ها ابزار اصلی ذخیره سازی طولانی مدت هستند.
شبکه های عصبی می توانند وزن ها را به منظور بهبود عملکرد یک کار خاص، تنظیم نمایند.
یک گره از چندین ورودی از سایر گره ها و از چندین خروجی و از یک تابع غیر خطی (تابع فعال) تشکیل شده است.
شبکه های عصبی به دو گروه Feed forward و Feedback تقسیم بندی می شوند.

دو نوع الگوریتم یادگیری در شبکه های عصبی

Supervised
Unsupervised

شبکه پرسپترون چند لایه و الگوریتم یادگیری آن

شبکه پرسپترون چند لایه و الگوریتم یادگیری آن

الگوریتم یادگیری Error Back propagation
ارزیابی تغییرات وزن

سیستم های فازی و شبکه های عصبی

هر دو روش مکمل یکدیگرند
شبکه های عصبی قابلیت یادگیری از داده ها را دارند در حالی که سیستم های فازی نمی توانند.
فهم سیستم های فازی به دلیل استفاده از اصطلاحات زبان شناسی و قوانین اگر – آنگاه می باشند در حالی که شبکه های عصبی اینگونه نیستند.
شبکه های عصبی قابلیت یادگیری سطح پایین و توان محاسباتی بالایی
سیستم های فازی قابلیت تفکر انسان گونه ی سطح بالا

ANFIS

Adaptive Network-based Fuzzy Inference Systems

سیستم های تطبیقی استنتاجی فازی مبتنی بر شبکه

Adaptive Neural-fuzzy Inference System

سیستم های نورو- فازی تطبیقی

معرفی ANFISS

ANFIS مخفف adaptive network-based fuzzy inference system می باشد.
توسط دکتر راگر جانگ (Rogger Jang) درسال 1993 معرفی شد.
یک شبکه تطبيق پذير و قابل آموزشی است (خود را با داده های آموزشی تطبیق می دهد) که به لحاظ عملکرد کاملا مشابه سيستم استنتاج فازی است.
برای استفاده کارآمدتر می توان در آن از پارامترهای الگوریتم ژنتیک نیز استفاده نمود.
سیستم های ANFIS در اصل یک سیستم TSK (تاگاکی- سوگنو-کانگ) درجه 1 هستند.
ANFIS از الگوریتم یادگیری HYBRID استفاده می کند.
از آنجا که تعیین پارامترهاي توابع عضویت در قسمت مقدم قواعد و همچنین تعیین ضرائب قسمت تالی قواعد همانند تعیین وزنهاي شبکه عصبی است به کمک روش هایی مثل الگوریتم هاي پس انتشار خطا انجام می شود.

منبع

سیستم استنتاج فازی چیست؟ قسمت 1

سیستم استنتاج فازی چیست؟ قسمت 2

نوامبر 27, 2019/0 دیدگاه /توسط hgadmin

سیستم استنتاج فازی چیست؟ قسمت 1

آموزش های عمومی هوش مصنوعی

مقدمه

جهان واقعی پيچيده است و این پيچيدگی به طور كلی از عدم قطعيت آن ناشی می شود، انسان به خاطر داشتن قدرت تفکر قادر به درک ابهامات و پيچيدگی هاست. بسياری از مشکلات دنيای واقعی با نظریه مجموعه های كلاسيک قابل حل نيستند، در تئوری مجموعه كلاسيک یک عنصر یا عضو مجموعه است یا نيست یا صفر است یا یک. نقطه مقابل تئوری مجموعه كلاسيک تئوری فازی قرار دارد.

تئوری مجموعه فازی ابزاری قوی جهت مواجه با عدم قطعيت ناشی از ابهام است، اگرچه سيستم های فازی پدیده های غيرقطعی و نامشخص را توصيف می كنند با این حال خود تئوری فازی یک تئوری دقيق است.

آشنایی با سيستم استنتاج فازی، مزایا و معایب آن ها می تواند در طراحی سيستم های خبره فازی و خروجی تخمين زده شده توسط سيستم موثر باشد، در این نوشته پس از تعریف سيستم استنتاج فازی، الگوریتم های استنتاج ممدانی، سوگنو مقایسه و بررسی می شوند. با ما همراه باشید.

منطق فازی

منطق فازی اولين بار توسط آقای پروفسور لطفی زاده در رساله ای به نام «مجموعه های فازی – اطلاعات و كنترل» در سال 1965 معرفی گردید و در دهه 1970 رشد و كاربرد عملی پيدا كرد، بزرگترین رخدادهای این دهه توليد كنترل كننده های فازی برای سيستم های واقعی بود.

منطق فازی از كاربردهای موفق در درزمينه ی مجموعه های فازی است كه در آن متغيرها زبانی هستند نه عددی، منطق فازی در برابر منطق باینری یا ارسطویی قرار دارد كه همه چيز را فقط به دو صورت بله یا خير، سياه و سفيد، صفر و یک می بيند، این منطق در بازه بين صفر و یک تغيير می كند.

مزایا و معایب منطق فازی

از جمله مزایای منطق فازی می توان به موارد زیر اشاره نمود:

منطق فازی به تفکر و منطق انسان نزدیک است.
برنامه های طراحی شده با منطق فازی سریع و كم هزینه هستند.
به راحتی می تواند مدلسازی شوند.
به طور گسترده ای در سيستم های كنترل و پيش بينی تصميم قابل استفاده است.
برای توصيف پدیده های غيرقطعی و نامشخص به كار می روند.

از جمله معایب منطق فازی می توان به موارد زیر اشاره كرد:

قوانين منطق فازی توسط تجربه متخصص تعيين می شوند.
تجزیه و تحليل یک سيستم با منطق فازی دشوار است یعنی نمی توان قبل از واكنش آن را تخمين زد.
توابع توسط آزمون و خطا مشخص می شوند كه زمان بر هستند.

سيستم های استنتاج فازی

در شکل 1 معماری سيستم استنتاج فازی نشان داده شده است. همانطور كه مشخص است سيستم استنتاج فازی به طور كلی از اجزاء زیر ساخته شده است:

فازی ساز
موتور استنتاج فازی
دفازی ساز

روند تبدیل متغيرهای صریح به متغيرهای زبانی را فازی سازی می گویند. موتور استنتاج با استفاده از الگوریتم های استنتاج، قوانين را ارزیابی و استنتاج می كند و پس از تجميع قوانين خروجی توسط واحد دفازی ساز به مقدار صریح یا عددی تبدیل می شود.

انواع روش های دفازی سازی شامل مركز ثقل ناحيه (COA)، نيمساز ناحيه (BOA )، كوچکترین ماكزیمم (SOM)، بيشترین ماكزیمم (LOM )، ميانگين ماكزیمم (MOM)، ميانگين وزنی (WA)، مجموع وزنی (WS) می باشد كه به طور كلی COA و WA بيشترین كاربردها را دارد.

کاربردهای سيستم استنتاج فازی

استفاده از سيستم های فازی روز به روز گسترش یافت و كاربرد آن درزمينه های مختلفی مانند سيستمهای خبره فازی، سيستم های پشتيبانی تصميم، برآورد هزینه احتمالی پروژه با استفاده از تجزیه و تحليل ریسک، سيستمهای كنترل، پردازش تصویر، ارتباطات، بازرگانی، پزشکی، نظامی و آموزشی، رباتها، سيستم قدرت و رآكتور هسته ای و مهندسی خودرو به كار گرفته شد.

یکی از اولين محصولاتی كه از سيستم های فازی استفاده نمودند ماشين لباسشویی بود كه توسط شركت ماتسو شيتا در سال 1990 در ژاپن عرضه شد، در این ماشين لباسشویی از سيستم فازی برای تنظيم خودكار تعداد دورهای مناسب، بر اساس نوع، ميزان كثيفی و حجم لباس استفاده شد. سيستم كنترل فازی متروی سندایی نيز از دیگر كاربردهای سيستم فازی است كه چهار پارامتر، ایمنی، راحتی سرنشينان، رسيدن به سرعت مطلوب و دقت ترمز را به طور همزمان در نظر می گيرد. امروزه از سيستم فازی نيز در تثبيت كننده تصویر دیجيتال در دوربين ها و در بخش هایی نظير موتور، انتقال نيرو و ترمز در اتومبيل ها، تغييرات دنده خودكار و تصفيه آب استفاده شده است .

انواع الگوریتم های استنتاج فازی

1-الگوریتم استنتاج ممدانی

سيستم استنتاج ممدانی را ممدانی و اسيليان در سال 1975 پيشنهاد دادند. این سيستم ها به دليل داشتن طبيعت بصری و تفسيری از قوانين می توانند به طور گسترده ای در سيستم های پشتيبانی تصميم استفاده شوند، همچنين دارای قدرت بيانی بالایی هستند و می توانند به هر دو صورت چند ورودی و چند خروجی (MIMO) و چند ورودی و یک خروجی(MISO) پياده سازی می شود.

دیاگرام كلی سيستم استنتاج فازی ممدانی در شکل 2 نشان داده شده است، سيستم استنتاج ممدانی از مجموعه های فازی به عنوان نتيجه قانون استفاده می كند و خروجی هر قانون به صورت غيرخطی و فازی است. همچنين از لحاظ روش دفازی سازی با بقيه سيستم های استنتاج متفاوت است. روش های دفازی سازی در سيستم استنتاج ممدانی به صورت BOA، COA، SOM, ،LOM, ،MOM هستند.

فرم كلی قوانين در سيستم ممدانی در شکل 3 نشان داده شده است، نتایج هر قانون كه با مقدارهای c1 و c2 مشخص می باشند، همانطور كه مشخص است پس ازتجميع نتایج حاصل از قوانين، عمل دفازی سازی بر روی تابع عضویت خروجی z انجام می گيرد و نتایج به صورت عددی به دست می آید.

اجرای قوانین در سیستم استنتاج فازی ممدانی — شکل 3 :فرم كلی اجرای قوانين در سيستم استنتاج ممدانی

2- الگوریتم استنتاج تاکاگی سوگنو

سيستم استنتاج تاكاگی سوگنو، توسط تاكاگی و ميشيو سوگنو در سال 1985 به منظور توسعه یک رویکرد سيستماتيک برای توليد قوانين فازی ارائه شد، این سيستم استنتاج بيشتر در سيستم های كنترلی و در زمينه هایی كه نياز به محاسبات ریاضی باشد مورداستفاده قرار می گيرد. شکل 4 دیاگرام یک سيستم استنتاج سوگنو را نشان می دهد. خروجی الگوریتم استنتاج سوگنو از یک چند جمل های مرتبه اول از متغيرهای ورودی به عنوان نتيجه قانون استفاده می كند و روش دفازی سازی در آن از نوع روشهای دفازی سازی WS,WA می باشد، همچنين سيستم استنتاج سوگنو به صورت MISO پياده سازی می شود و نمی تواند به صورت MIMO پياده سازی شود.

شمای كلی ارزیابی قوانين با استفاده از روش سوگنو در شکل 1 نشان داده شده است. همانطور كه مشخص است نتایج قانون در سيستم استنتاج سوگنو به صورت صریح و خطی می باشد.

نمای کلی از اجرای قوانین در سیستم استنتاج سوگنو

مقایسه الگوریتم استنتاج فازی ممدانی و سوگنو

در جدول (1) مقایسه ای بين الگوریتم های استنتاج ممدانی و سوگنو نشان داده شده است. الگوریتم استنتاج سوگنو بيشتر در سيستم های كنترلی و سيستم هایی كه احتياج به محاسبات ریاضی دارند استفاده می شود اما در الگوریتم استنتاج ممدانی نتایج منطقی با یک ساختار نسبتاً ساده بيان می شود و بيشتر در سيستم های پشتيبانی تصميم و سيستم هایی كه قابليت تفسيری از قوانين را دارند استفاده می شوند، خروجی الگوریتم استنتاج ممدانی غيرخطی و فازی است اما خروجی سيستم استنتاج سوگنو خطی است، الگوریتم ممدانی در بسياری از عملکردها كه دقت خروجی و انعطاف پذیری مهم است به خوبی عمل نمی كند ولی موتور استنتاج تاكاگی سوگنو انعطاف پذیرتر و از دقت عملکرد بالاتری برخوردار می باشد و از لحاظ محاسباتی نسبت به ممدانی مؤثرتر است، زیرا فرایند دفازی سازی به زمان محاسباتی كمتری نياز دارد، اما فقط برای تجزیه وتحليل سيستم های كنترلی MISO خطی بهتر عمل می كند.

مقایسه بین الگوریتم های استنتاج فازی ممدانی و سوگنو

نتيجه گيری

امروزه كاربردهای فازی در طراحی های مختلف سيستم های غيرقطعی، نشان دهنده عملکرد بالا و رشد سریع این سيستم ها است، هرچند كه علمکرد الگوریتم های استنتاج فازی مشابه هم هستند اما رعایت تفاوت های آنها در طراحی سيستم های فازی می تواند در خروجی سيستم مؤثر باشد، الگوریتم استنتاج سوگنو به خاطر داشتن دقت و انعطاف پذیری بالا درطراحی سيستم های حساس و كنترلی استفاده می شود ولی سيستم های ممدانی به خاطر خاصيت تفسيری و خروجی فازی كه از قوانين دارند بيشتر در زمينه سيستم های انسانی استفاده می شوند.

منبع : مقاله مروری بر الگوریتم های استنتاج فازی نویسندگان: عالمه جعفری سوق، حامد شهبازی

مروری بر الگوریتم های استنتاج فازی دریافت

هم چنین برای دریافت اطلاعات بیشتر می توانید فایل آموزشی سیستم های استنتاج فازی تهیه شده توسط دکتر اکبری را از لینک زیر دریافت نمایید.

Fuzzy Inference Systems دریافت

سيستم استنتاج فازي

سيستمي كه يك نگاشت از ورودي به خروجي را با استفاده از منطق فاز فرموله ميكند به نام سيستم استنتاج فازي (FIS) شناخته مي شود. سيستم استنتاج فازي همچنين به نام سيستم مبتني بر قواعد نيز ناميده مي شود .زيرا اين سيستم ها از تعدادي عبارت « اگر – آنگاه » ساخته شده است. وقتي چنين سيستم هايي در نقش كنترلي ظاهر مي شوند به آنها كنترل كننده های فازی می گويند .معماري اصلي FIS از پنج بلوك تابع تشكيل شده كه در شكل زير نشان داده شده است:

پايگاه قواعد ( Rule base) : شامل قواعد و عبارات «‌اگر – آنگاه » فازي

پايگاه داده (Dara base) : تعريف توابع عضويت

واحد تصميم گيري ( Decision making unit)‌: انجام عمليات روي قواعد فازي

رابط فازي ساز ( Fazzification inter face)‌: تبديل ورودي هاي حقيقي به مجموعه هاي فازي

رابط غير فازي ساز ( Defazzification inter face)‌ : تبديل نتايج فازي به مقادير حقيقي

دو واحد پايگاه داده و پايگاه قواعد با هم تحت عنوان پايگاه دانش (Knowledge base) شناخته مي شوند. سيستم هاي استنتاج فازي را مي توان به سه كلاس « ممداني (mamdani) » ، «‌سوگنو (sugeno) » و «‌تاكاگي (Takagi)» تقسيم كرد.

بسياري از FIS ها از نوع ممداني هستند كه در اين نوع ، اعضاي مجموعة فازي خروجي را پيش بيني مي كنند .

برای کار کردن با بخش فازی در Matlab درخط فرمان متلب عبارت fuzzy<< را تایپ کنید و یا در بخش command کلمه fuzzy را تایپ کرده اینتر میزنیم .صفحه ای به صورت زیر باز می شود .

تعریف متغیر ها

در این صفحه از طریق منوی Edit تعداد ورودی ها و خروجی های مورد نظر را وارد می کنیم .با وارد کردن ورودی ها و خروجی ها به شکل زیر می رسیم.

تعریف توابع عضویت

بعد از تعیین ورودی ها و خروجی ها باید تابع عضویت را برای هر یک از آنها تعین کنیم برای این منظور از منوی Edit وارد قسمت membership function می شویم و با کلید روی هر متغیر تابع عضویت آن را تنظیم می کنیم . در زیر نمای بخش membership function آمده است . توابع عضویت را با استفاده از المان های موجود می توان تغییر داد.

از قسمت Type میتوان نوع تابع عضویت را تغییر داد و از قسم params میتوان پارامترهای مربوط به تابع عضویت را تغییر داد:

تعریف rule ها

بعد از تعی ن membership function باید Ruleها را تعریف کنیم. برای این کار از منوی edit وارد قسمت Rule شده و شروع به تعریف Rule ها می کنیم.

بررسی

بعد از تعریف Rule ها نوبت به بررسی نتایج می رسد . برای بررسی نتایج از منوی view گزینه Rules را انتخاب می کنیم و در صفحه باز شده متغیرها و حاصل آنها را بر روی خرو جی ها می توان مشاهده کرد.

برای دیدن نمودارهای حاصل از بخش view قسمت Surface را انتخاب می کنیم .

منبع

سیستم استنتاج فازی چیست؟ قسمت 1

سیستم استنتاج فازی چیست؟ قسمت 2

نوامبر 26, 2019/2 دیدگاه /توسط daliri

دوربین دیجیتال چیست؟ قسمت 3

دوربین (camera)

اصلاح دیجیتالی عکس در دوربین

عکس دیجیتال عبارت از ارقام صفر ویک است که می توان به طریق الکترونیکی اندازه آنها را کم و زیاد کرد . این بدین معنی است که بلافاصله بعد ازاینکه اطلاعات مربوط به عکس در سنسور نوری ثبت و مشخص شد ، می توان این اطلاعات را ادیت یا تصحیح کرد . اینکه چه کارکردهایی در این رابطه وجود دارند و دست شما چقدر باز است ، بستگی به مدل دوربین دارد و در هر دوربینی فرق می کند . بنابراین جهت اطلاع از امکانات دوربین خود در این زمینه به دفترچه راهنمای آن مراجعه کنید .

اندازه عکس

در اکثر دوربینهای دیجیتال امکان عوض کردن اندازه عکس وجود دارد . این اندازه معمولا” به واحد پیکسل بیان می شود ،1920×2560،1200×1600،960×1280 و یا 480×640 ، هرچه اندازه قطع عکس را کوچک تر انتخاب کنید ، می توانید تعداد عکسهای بیشتری را روی کارت حافظه ذخیره کنید . یک عکس کوچک باعث می شود که ارسال آن ازطریق e-mail ساده تر و سریع تر صورت گیرد . اما از طرف دیگر این نوع عکس ها ، مناسب چاپ در قطع بزرگ نیستند .

کیفیت عکس

عکس در فرمت غیر فشرده ، فضای زیادی را اشغال خواهد کرد . اگر شما کیفیت پایین تری برای عکس انتخاب کنید می توانید اندازه فایل خود را با کمک برنامه های فشرده سازی کوچک کنید . البته در حالت فشرده کردن فایل مقداری از اطلاعات عکس حذف می شوند . کیفیتهای عادی عکس عبارتند از استاندارد ، نرمال ، خوب و RAW به معنی خام . حالت RAW که بهترین کیفیت عکس را ارائه می کند ، فرمت غیر فشرده عکس است که مخصوص دوربینی که با آن کار می کنید ، است .

وضوح عکس

دوربین می تواند وضوح عکس را جهت نشان دادن جزئیات بیشتر افزایش دهد . این مسئله را با فوکوس کردن مخلوط نکنید ، اینها دو مقوله جدا از هم هستند . اگر خطوط مرزی ( لبه های) سوژه سخت وغیر ظریف باشند ، جزئیاتی کمتر در عکس دیده می شوند . در حالت عادی ، قبل از اینکه عکس در کارت حافظه ضبط شود ، مقداری لبه های آن واضح تر می شوند .

تعادل نور سفید

چشم انسان به طور اتوماتیک به انواع نورهای موجود خود را تطبیق می دهد . یک صفحه کاغذ سفید را چشم ما چه در زیر نور آفتاب و چه در زیر نور لامپ های خانه سفید می بیند .برای دوربینهای ویدئو و یا دوربینهای عکاسی دیجیتال ، باید معادل نور سفید را روی آنها تنظیم کرد . این بدین معنی است که روش دوربین برای ثبت رنگهای مختلف باید طوری تنظیم شود که رنگ سفید یا خاکستری سوژه هم به طور خنثی درروی عکس به رنگ سفید یا خاکستری ظاهر شوند .

حالت رنگ

بعضی از دوربینها دارای قابلیت عکاسی در حالت رنگ های مختلف مثل سیاه و سفید ، غلظت رنگ بالا و یا پایین و یا تون قهوه ای رنگ معروف به سپیا (Sepia )هستند .

حساسیت به نور

در دوربینهای معمولی که با فیلم کار می کنند و در این کتاب دوربینهای آنالوگ نامیده می شوند ، می توان حساسیت فیلم را مناسب نوع فیلمی که به کار می برید ، انتخاب وتنظیم کرد . هرچه حساسیت فیلم پایین تر باشد ، دانه هایی که روی فیلم هستند ریزتر و جزئیات زیادتری از سوژه در عکس ثبت می شوند . واحد حساسیت فیلم به ISO بیان می شود که ترکیبی از سیستم آمریکایی ASA وسیستم آلمانی DIN است . مثلا” 400/27˚ ISO واحدی برای نمایش فیلم با حساسیت 400 ایزو است .

در یک دوربین عکاسی دیجیتال باید دید که کارخانه سازنده آن چه حساسیتی را برا ی آن مدل در نظر گرفته است. هر اندازه ای که دوربین برای آن تنظیم و ساخته شده باشد، همه عکسها بر مبنای آن حساسیت گرفته خواهند شد. حساسیت برای یک سنسور نوری CCD به صورت ISO بیان می شود. حساسیت سنسور نوری در دوربین های دیجتال کمپکت معمولا” 100 ایزو است. بعضی از دوربینها دارای قابلیت تغییر ایزو یا حساسیت فیلم از طریق تقویت سیگنالهای الکترونیکی هستند. این کارکرد باعث می شود که حتی در زیر نور ضعیف هم بتوان عکاسی کرد ولی عکسی که شما دریافت خواهید کرد، دارای برفک و پارازیت خواهد بود.

کار روی عکسها درون دوربین

دوربین دیجیتال در حقیقت کامپیوتر کوچکی است که با آن نه تنها می توان عکس گرفت ، بلکه می توان در سازماندهی و نشان دادن عکسها هم از آن استفاده کرد. امکانات موجود در دوربینهای مختلف فرق می کنند در زیر چند نمونه مرسوم آنها آورده می شوند.

ذخیره عکسها در پوشه های مختلف

یک کارت حافظه دوربین می تواند دهها و بلکه صدها عکس را در خود جای دهد. در بسیاری مواقع ، بهتر است که عکسها را در پوشه ها ی مختلف کارت ذخیره کرد. مثلا” فرض کنیم که می خواهید به یک مسافرت دور اروپا بروید و از شهرهای چند کشور مختلف دیدن کنید. از طریق سازمان دادن و درست کردن پوشه های مختلف و جای دادن عکسها درون آنها، راحت تر می توانید به خاطر بیاورید که کدام عکس را در چه محلی انداخته اید. به این طریق، نمایش دادن عکسها هم کار راحت تری خواهد بود و هر زمان که تصمیم به نمایش عکس های شهر مشخصی بگیرید، می توانید بلافاصله و سریع به پوشه شهر مربوطه بروید.

تنظیم نامگذاری عکسها

بعضی از دوربینها از نامگذاری استاندارد استفاده می کنند، یعنی یک فایل عکس را با یک حرف و سه یا چهار شماره نامگذاری می کنند . زمانیکه ارقام تمام شدند، مجددا” دوربین از صفر شروع می کند. بعضی دیگر از مدلها به محض اینکه کارت حافظه جدید را در آن می گذارید، کنتور شماره عکس صفر می شود و شماره ها از نوع شروع می شوند. در اینگونه مدلها زمانیکه عکسهای خود را از دوربین به کامپیوتر منتقل می کنید، خطر این وجود دارد که عکسهای هم نام سابق حذف و عکسهای جدید جایگزین آنها شوند. به این دلیل حتما” کنترل کنید که آیا، دوربین شما می تواند شماره پشت سر هم به عکسها بدهد ، بدون اینکه کنتور آن صفر شود یا نه. یک راه مناسب جهت مقابله با این خطر، این هست که عکسها را در پوشه های خاص خود ذخیره کنید و همه عکسهای قدیمی و جدید در یک پوشه ذخیره نشوند.

حذف کردن عکسها

عکسهای ناجور و نامطلوب را می توانید بلافاصله پس از رویت پاک کنید. هم چنین می توانید در پایان یک روز همراه با عکاسی ، عکسها را یک به یک رویت کنید و آنهایی را که نمی خواهید، پاک کنید. به این طریق می توانید، جا برای عکسهای جدید خود ایجاد کنید.

منبع

دوربین های دیجیتال:

دوربین ۳۶۰ درجه ی ozo محصول نوکیا

دوربین دیجیتال دوربین هایی هستند که برای گرفتن عکس و ذخیره آن بجای فیلم عکاسی از حسگرهای حساس به نور معمولاً از نوع CCD یا CMOS استفاده می‌کند و تصویر گرفته شده توسط سنسور طی چند مرحله به حافظهٔ دوربین برای استفاده فرستاده می‌شود.

تاریخچه:

در سال ۱۹۷۵ اولین دوربین دیجیتال جهان توسط استیون ساسون (Steve Sasson) یکی از مهندسان شرکت ایستمن کداک (Eastman Kodak) ساخته شد. این ابزار ۳٫۶ کیلوگرمی می توانست عکس‌های ۰٫۰۱ مگاپیکسلی خود را بر روی یک نوار کاست ضبط کند و نوردهی هر عکس به ۲۳ ثانیه زمان نیاز داشت.

اولین دوربین دیجیتال دنیا

عملکرد:

گرچه اصول کلی این دوربین‌ها شبیه به دوربین‌های فیلمی هستند، نحوه کار داخل این دوربین‌ها کاملاً متفاوت است. در این دوربین‌ها تصویر توسط یک سنسور CCD یا یک CMOS گرفته می‌شود. CCD بصورت ردیفها و ستونهایی از سنسورهای نقطه‌ای نور هستند که هر چه تعداد این نقاط بیشتر و فشرده تر باشد، تصویر دارای دقت بالاتری است) هر سنسور نور را به ولتاژی متناسب با درخشندگی نور تبدیل کرده و آن را به بخش تبدیل سیگنال‌های آنالوگ به دیجیتال ADC می‌فرستد که در آنجا نوسانات دریافتی از CCD به کدهای مجزای باینری(عددهای مبنای دو بصورت صفر و یک) تبدیل می‌شود. خروجی دیجیتال از ADC به یک پردازنده سیگنال‌های دیجیتال DSP فرستاده می‌شود که کنتراست و جزئیات تصویر در آن تنظیم می‌شود و قبل از فرستادن تصویر به حافظه برای ذخیره تصویر، اطلاعات را به یک فایل فشرده تبدیل می‌کند. هر چه نور درخشنده‌تر باشد، ولتاژ بالاتری تولید شده و در نتیجه پیکسل‌های رایانه‌ای روشن‌تری ایجاد می‌شود. هر چه تعداد این سنسورها که به‌صورت نقطه هستند بیشتر باشد، وضوح تصویر به دست آمده بیشتر است و جزئیات بیشتری از تصویر گرفته می‌شود.

سنسورهای CCD و CMOS

دوربین‌های دیجیتال برای دریافت نور از یک تصویر دیجیتالی، از سنسورهای مشخصی استفاده می‌کنند که معمولاً CCD (افزاره ی بار جفت ‌شده) یا CMOS (نیم رسانای اکسید فلزی مکمل) نامیده می‌شوند. هر دو سنسورهای نام‌برده شده در اغلب دوربین‌های دیجیتال استفاده‌شده و ابزاری مناسب برای گرفتن تصاویر دیجیتالی به حساب می‌آیند. سنسورهای CCD و CMOS به طور معمول به اندازه‌ی یک ناخن انگشت بوده و تماماً از سیلیکون ساخته‌شده‌اند. سطح این سنسورها شامل میلیون‌ها دیود فوق‌العاده کوچک است که هر کدام یک پیکسل از تصاویر گرفته‌شده توسط لنز دوربین را ثبت می‌کنند. به طور کلی دیودهای بیشتر بر روی سطح یک دوربین دیجیتال برابر است باکیفیت بهتر تصاویر گرفته‌شده توسط آن دوربین! جالب است بدانید واژه‌ی مگا پیکسل در مشخصات یک دوربین حاکی از تعداد سنسورهای موجود بر روی سطح CCD یا CMOS است.

تفاوت دیجیتال و آنالوگ چیست؟

در فناوری آنالوگ، امواج و یا سیگنال به شکل اولیه ضبط و یا استفاده میشوند. برای مثال در یک دستگاه ضبط صوت آنالوگ سیگنال دریافت شده مستقیما از میکروفون دریافت و به نوار کاست منتقل میشود. صوت شما که از میکروفن دریافت میشود به صورت طبیعی یا همان آنالوگ است و امواج ضبط شده بر روی نوار کاست نیزبه همین صورت (آنالوگ) خواهد بود. این امواج میتواند از روی نوار خوانده و یا تقویت شوند و برای تولید صدا به بلندگو ها فرستاده شوند. واژه انالوگ از واژه یونانی ΑΝΆΛΟΓΟΣ که معنای “نسبی” می دهد گرفته شده است.

در فناوری دیجیتال امواج نمونه ای از امواج آنالوگ در یک سری از فواصل میشوند. سپس تبدیل به یک سری اعداد(صفر و یک) میشوند که توانایی ذخیره شدن روی دستگاه های دیجیتالی را خواهند داشت.

در یک سی دی میزان این نمونه سازی ۴۴۰۰۰ نمونه (سیگنال) در هر ثانیه است. به عبارت دیگر ۴۴۰۰۰ شماره در هر ثانیه از یک موسیقی توسط دستگاه خوانده میشود. برای شنیدن موسیقی اعداد به صورت امواج ولتاژ(مستقیم یا متناوب) در می آیند که به صوت اصلی بسیار نزدیک است.

واژه دیجیتال از لغت DIGIT (رقم) ویا DIGITUS (واژه پونانی به معنی انگشت) گرفته شده، بخاطر اینکه از انگشتان برای شمارش استفاده میشود.

تصاویر رنگی در دوربین های دیجیتال:

برای ثبت عکس‌های رنگی، بر روی هر سنسور یک فیلتر نصب می‌شود که اجازه عبور رنگ‌های نوری معینی را می‌دهد. در واقع همه دوربین‌های دیجیتال موجود در زمان حاضرتنها می‌توانند یکی از سه رنگ اصلی را در هر سنسور دریافت کنند و در نتیجه این که تقریبا از سه تا رنگ اصلی دوتای آن دور ریخته می‌شود. برای جبران این موضوع دوربین باید دو رنگ اصلی دیگر را تخمین بزند تا بتواند رنگ کاملی در هر پیکسل به دست آورد. معمول ترین روش برای کار استفاده از آرایه فیلتر رنگ است که یکی از آنها به نام «فیلتر بایر» را در تصویر زیر مشاهده می‌کنید.

فیلتر بایر از ردیف‌های فیلتر سبز-قرمز و سبز-آبی تشکیل شده است. دقت کنید که تعداد سنسورهای سبز در فیلتر بایر دو برابر سنسورهای قرمز و آبی است. دلیل این انتخاب با ساختار چشم و حساسیت بیشتر آن به نور سبز باز می‌گردد. بیشتر بودن تعداد فیلترهای سبز منجر به تولید عکسی با نویز کمتر و جزئیات بیشتر می‌شود.

لازم است بدانید تمام دوربین‌های دیجیتال از فیلتر بایر استفاده نمی‌کنند، اما تا کنون این الگوریتم متداول‌ترین روش بوده است.

منبع

منابع

دوربین دیجیتال چیست؟ قسمت 1
دوربین دیجیتال چیست؟ قسمت 2
دوربین دیجیتال چیست؟ قسمت 3

نوامبر 22, 2019/0 دیدگاه /توسط hgadmin

مدل مخفی مارکوف (Hidden Markov Model) قسمت 4

دسته‌بندی نشده

مسئله کد گشایی و الگوریتم ویتربی (Viterbi Algorithm)

در این حالت می‌خواهیم با داشتن دنباله مشاهدات $O=\{O_{1},...,O_{t}\}$ و مدل $lambda=\{A,B,\pi \}$ دنباله حالات بهینه $Q=\{q_{1},...,q_{t}\}$ برای تولید $O=\{O_{1},...,O_{t}\}$ را به‌دست آوریم.

یک راه حل این است که محتمل‌ترین حالت در لحظه t را به‌دست آوریم و تمام حالات را به این شکل برای دنبالهٔ ورودی به‌دست آوریم. اما برخی مواقع این روش به ما یک دنبالهٔ معتبر و بامعنا از حالات را نمی‌دهد. به همین دلیل، باید راهی پیدا کرد که یک چنین مشکلی نداشته باشد.

در یکی از این روش‌ها که با نام الگوریتم Viterbi شناخته می‌شود، دنباله حالات کامل با بیشترین مقدار نسبت شباهت پیدا می‌شود. در این روش برای ساده کردن محاسبات متغیر کمکی زیر را تعریف می‌نماییم.

$\delta _{t}(i)=maxp\{q_{1},q_{2},...,q_{t-1},q_{t}=t,o_{1},o_{2},...,o_{t-1}|\lambda \}$

که در شرایطی که حالت فعلی برابر با i باشد، بیشترین مقدار احتمال برای دنباله حالات و دنباله مشاهدات در زمان t را می‌دهد. به همین ترتیب می‌توان روابط بازگشتی زیر را نیز به‌دست‌آورد.

$\delta _{t+1}(j)=b_{j}(o_{t+1})[max\delta _{t}(i)a_{ij}],\qquad 1\leq i\leq N,\qquad 1\leq t\leq T-1$

که در آن

$\delta _{1}(j)=\pi _{j}b_{j}(o_{1}),\qquad 1\leq i\leq N$

به همین دلیل روال پیدا کردن دنباله حالات با بیشترین احتمال از محاسبهٔ مقدار $\delta _{j}(i),i\leq j\leq N$ و با کمک رابطهٔ فوق شروع می‌شود. در این روش در هر زمان یک اشاره گر به حالت برنده قبلی خواهیم داشت. در نهایت حالت $\ j^{*}$ را با داشتن شرط زیر به‌دست می‌آوریم.

$\ j^{*}=argmax\delta _{T}(i),$

و با شروع از حالت $\ j^{*}$ ، دنباله حالات به شکل بازگشت به عقب و با دنبال کردن اشاره گر به حالات قبلی به‌دست می‌آید. با استفاده از این روش می‌توان مجموعه حالات مورد نظر را به‌دست‌آورد. این الگوریتم را می‌توان به صورت یک جستجو در گراف که نودهای آن برابر با حالتها مدل HMM در هر لحظه از زمان می‌باشند نیز تفسیر نمود

مسئله یادگیری

به‌طور کلی مسئله یادگیری به این موضوع می‌پردازد که چگونه می‌توان پارامترهای مدل HMM را تخمین زد تا مجموعه داده‌های آموزشی به بهترین نحو به کمک مدل HMM برای یک کاربرد مشخص بازنمایی شوند. به همین دلیل می‌توان نتیجه گرفت که میزان بهینه بودن مدل HMM برای کاربردهای مختلف، متفاوت است. به بیان دیگر می‌توان از چندین معیار بهینه‌سازی متفاوت استفاده نمود، که از این بین یکی برای کاربرد مورد نظر مناسب تر است. دو معیار بهینه‌سازی مختلف برای آموزش مدل HMM وجود دارد که شامل معیار بیشترین شباهت (ML) و معیار ماکزیمم اطلاعات متقابل ((Maximum Mutual Information (MMI) می‌باشند. آموزش به کمک هر یک از این معیارها در ادامه توضیح داده شده‌است.

معیار بیشترین شباهت((Maximum Likelihood (ML)

در معیار ML ما سعی داریم که احتمال یک دنباله ورودی $\ O^{w}$ که به کلاس w تعلق دارد را با داشتن مدل HMM همان کلاس به‌دست آوریم. این میزان احتمال برابر با نسبت شباهت کلی دنبالهٔ مشاهدات است و به صورت زیر محاسبه می‌شود.

$\ L_{tot}=p\{O^{w}|\lambda _{w}\}$

با توجه به رابطه فوق در حالت کلی معیار ML به صورت زیر تعریف می‌شود.

$\ L_{tot}=p\{O|\lambda \}$

اگر چه هیچ راه حل تحلیلی مناسبی برای مدل $\lambda =\{A,B,\pi \}$ وجود ندارد که مقدار $\ L_{tot}$ را ماکزیمم نماید، لیکن می‌توانیم با استفاده از یک روال بازگشتی پارامترهای مدل را به شکلی انتخاب کنیم که مقدار ماکزیمم به‌دست آید. روش Baum-Welch یا روش مبتنی بر گرادیان از جملهٔ این روش‌ها هستند.

الگوریتم بام- ولش

این روش را می‌توان به سادگی و با محاسبه احتمال رخداد پارامترها یا با محاسبه حداکثر رابطه زیر بر روی ${\bar {\lambda }}$ تعریف نمود.

$\ Q(\lambda ,{\bar {\lambda }})=\sum _{q}p\{q|O,\lambda \}log[p\{O,q,{\bar {\lambda }}\}]$

یکی از ویژگی‌های مخصوص این الگوریتم این است که همگرایی در آن تضمین شده‌است. برای توصیف این الگوریتم که به الگوریتم پیشرو- پسرو نیز معروف است، باید علاوه بر متغیرهای کمکی پیشرو و پسرو که قبلاً تعریف شده‌اند، متغیرهای کمکی بیشتری تعریف شود. البته می‌توان این متغیرها را در قالب متغیرهای پیشرو و پسرو نیز تعریف نمود.

اولین متغیر از این دست احتمال بودن در حالت i در زمان t و در حالت j در زمان t+1 است، که به صورت زیر تعریف می‌شود.

$\xi _{t}(i,j)=p\{{qt}=i,q_{t+1}=j|O,\lambda \}$

این تعریف با تعریف زیر معادل است.

$\xi _{t}(i,j)={\frac {p\{q_{t}=i,q_{t+1}=j,O|\lambda \}}{p\{O|\lambda \}}}$

می‌توان این متغیر را با استفاده از متغیرهای پیشرو و پسرو به صورت زیر تعریف نمود.

$\xi _{t}(i,j)={\frac {\alpha _{t}(i)a_{ij}\beta _{t+1}(j)b_{j}(o_{t+1})}{\sum _{i=1}^{N}\sum _{j=1}^{N}\alpha _{t}(i)a_{ij}\beta _{t+1}(j)b_{j}(o_{t+1})}}$

متغیر دوم بیانگر احتمال پسین حالت i با داشتن دنباله مشاهدات و مدل مخفی مارکوف می‌باشد و به صورت زیر بیان می‌شود.

$\gamma _{t}(i)=p\{q_{t}=i|O,\lambda \}$

این متغیر را نیز می‌توان در قالب متغیرهای پیشرو و پسرو تعریف نمود.

$\gamma _{t}(i)=\left[{\frac {\alpha _{t}(i)\beta _{t}(i)}{\sum _{i=1}^{N}\alpha _{t}(i)\beta _{t}(i)}}\right]$

رابطه بین دو متغیر فوق به صورت زیر بیان می‌شود.

$\gamma _{t}(i)=\sum _{i=1}^{N}\xi _{t}(i,j),\qquad 1\leq i\leq N,\qquad 1\leq t\leq M$

اکنون می‌توان الگوریتم آموزش بام – ولش را با ماکزیمم کردن مقدار به‌دست‌آورد. اگر مدل اولیهٔ ما باشد، می‌توانیم متغیرهای پسرو و پیشرو و متغیرهای $\xi$ و $\gamma$ را تعریف نمود. مرحلهٔ بعدی این است که پارامترهای مدل را با توجه به روابط بازتخمین زیر به‌روزرسانی کنیم.

${\bar {\pi }}_{i}=\gamma _{1}(i),\qquad 1\leq i\leq N$

${\bar {a}}_{ij}={\frac {\sum _{t=1}^{T-1}\xi _{t}(i,j)}{\sum _{t=1}^{T-1}\gamma _{t}(i)}},\qquad 1\leq i\leq N,\qquad 1\leq j\leq N$

${\bar {b}}_{j}(k)={\frac {\sum _{t=1}^{T}\gamma _{t}(j)}{\sum _{t=1}^{T}\gamma _{t}(j)}},\qquad 1\leq j\leq N,\qquad 1\leq k\leq M$

فرمول‌های بازتخمین را می‌توان به‌راحتی به شکلی تغییر داد که با توابع چگالی پیوسته نیز قابل استفاده باشند.

الگوریتم حداکثرسازی امید ریاضی (Expectation Maximization)

الگوریتم حداکثرسازی امید ریاضی یا EM به عنوان یک نمونه از الگوریتم بام – ولش در آموزش مدل‌های HMM مورد استفاده قرار می‌گیرد. الگوریتم EM دارای دو فاز تحت عنوان Expectation و Maximization است. مراحل آموزش مدل در الگوریتم EM به صورت زیر است.

مرحله مقدار دهی اولیه: پارامترهای اولیه مدل $\lambda$ را تعیین می‌نماییم.
مرحله امید ریاضی(Expectation): برای مدل $\lambda$ موارد زیر را محاسبه می‌کنیم.

$\alpha$ مقادیر با استفاده از الگوریتم پیشرو
مقادیر $\beta$ و $\gamma$ با استفاده از الگوریتم پسرو

مرحله ماکزیمم‌سازی (Maximization): مدل $\lambda$ را با استفاده از الگوریتم باز تخمین محاسبه می‌نماییم.
مرحله بروزرسانی $\lambda \leftarrow {\acute {\lambda }}$
بازگشت به مرحله امید ریاضی

روال فوق تا زمانی که میزان نسبت شباهت نسبت به مرحله قبل بهبود مناسبی داشته باشد ادامه می‌یابد.

روش مبتنی بر گرادیان

در روش مبتنی بر گرادیان هر پارامتر $\ \Theta$ از مدل $\ \lambda$ با توجه به رابطه زیر تغییر داده می‌شود.

$\ \Theta ^{new}=\Theta ^{old}-\eta \left[{\frac {\partial j}{\partial \Theta }}\right]$

که در آن مقدار J با ید مینیمم شود. در این حالت خواهیم داشت.

$\ J=E_{ML}=-\log(P{O|\lambda })=-\log L_{tot}$

از آنجا که مینیمم کردن J معادل است با مینیمم کردن $\ L_{tot}$ نیاز است است تا معیار ML بهینه به‌دست آید. آنگاه مسئله، یافتن مقدار مشتق $\ \left({\frac {\partial J}{\partial \Theta }}\right)$ برای تمام پارامترهای $\ \Theta$ از مدل است. این کار را می‌توان به سادگی با استفاده از مقدار $\ L_{tot}$

$\ L_{tot}=\sum _{i=1}^{N}p(O,q_{t}=i|\lambda )=\sum _{i=1}^{N}\alpha _{t}(i)\mathrm {B} _{t}(i)$

با مشتق گرفتن از رابطهٔ قبل به این نتیجه دست می‌یابیم:

$\ \left({\frac {\partial J}{\partial \Theta }}\right)=-\left({\frac {1}{L_{tot}}}\right)\left({\frac {\partial L_{tot}}{\partial \Theta }}\right)$

از آنجا که در رابطهٔ فوق مقدار $\ \left({\frac {\partial J}{\partial \Theta }}\right)$ بر حسب $\ \left({\frac {\partial L_{tot}}{\partial \Theta }}\right)$ به‌دست می‌آید، می‌توان رابطه $\ \left({\frac {\partial J}{\partial \Theta }}\right)$ به‌دست‌آورد.

در روش مبتنی بر گرادیان، مقدار $\ \left({\frac {\partial L_{tot}}{\partial \Theta }}\right)$ را باید برای پارامترهای $\ a_{g}$ (احتمال انتقال) و $\ b_{g}$ (احتمال مشاهدات) به‌دست‌آورد.

استفاده از مدل HMM در شناسایی گفتار

بحث شناسایی اتوماتیک گفتار را می‌توان از دو جنبه مورد بررسی قرار داد.

از جنبه تولید گفتار
از جنبه فهم و دریافت گفتار

مدل مخفی مارکوف (HMM) تلاشی است برای مدل‌سازی آماری دستگاه تولید گفتار و به همین دلیل به اولین دسته از روش‌های شناسایی گفتار تعلق دارد. در طول چندین سال گذشته این روش به عنوان موفقترین روش در شناسایی گفتار مورد استفاده قرار گرفته‌است. دلیل اصلی این مسئله این است که مدل HMM قادر است به شکل بسیار خوبی خصوصیات سیگنال گفتار را در یک قالب ریاضی قابل فهم تعریف نماید.

در یک سیستم ASR مبتنی بر HMM قبل از آموزش HMM یک مرحله استخراج ویژگی‌ها انجام می‌گردد. به این ترتیب ورودی HMM یک دنباله گسسته از پارامترهای برداری است. بردارهای ویژگی می‌تواند به یکی از دو طریق بردارهای چندی‌سازی شده یا مقادیر پیوسته به مدل HMM آموزش داده شوند. می‌توان مدل HMM را به گونه‌ای طراحی نمود که هر یک از این انواع ورودیها را دریافت نماید. مسئله مهم این است که مدل HMM چگونه با طبیعت تصادفی مقادیر بردار ویژگی سازگاری پیدا خواهد کرد.

استفاده از HMM در شناسایی کلمات جداگانه

در حالت کلی شناسایی واحدهای گفتاری جدا از هم به کاربردی اطلاق می‌شود که در آن یک کلمه، یک زیر کلمه یا دنباله‌ای از کلمات به صورت جداگانه و به تنهایی شناسایی شود. باید توجه داشت که این تعریف با مسئله شناسایی گفتار گسسته که در آن گفتار به صورت گسسته بیان می‌شود متفاوت است. در این بین شناسایی کلمات جداگانه کاربرد بیشتری به نسبت دو مورد دیگر دارد و دو مورد دیگر بیشتر در عرصه مطالعات تئوری مورد بررسی قرار می‌گیرند. برای این کاربرد راه حلهای مختلفی وجود دارد زیرا معیارهای بهینه‌سازی متفاوتی را برای این منظور معرفی شده‌است و الگوریتمهای پیاده‌سازی شده مختلفی نیز برای هر معیار موجود است. این مسئله را از دو جنبه آموزش و شناسایی مورد بررسی قرار می‌دهیم.

آموزش

فرض می‌کنیم که فاز پیش پردازش سیستم دنباله مشاهدات زیر را تولید نماید:

$\ O=(o_{1},o_{2},....,o_{N})$

پارامترهای اولیه تمام مدل‌های HMM را با یک مجموعه از مقادیر مشخص مقدار دهی می‌نماییم.

$\ \lambda _{i},1\leq i\leq N$

در آغاز این مسئله را برای حالت clamped در نظر بگیرید. از آنجایی که ما برای هر کلاس از واحدها یک HMM داریم، می‌توانیم مدل $\ \lambda _{i}$ از کلاس l را که دنباله مشاهدات فعلی به آن مربوط می‌شود، را انتخاب نماییم.

$\ L_{tot}^{clamped}=\sum _{i\in \lambda _{i}}\alpha _{t}(i)\mathrm {B} _{t}(i)=\sum _{i\in \lambda _{i}}\alpha _{T}(i)$

برای حالت free نیز به مانند حالت قبل می‌توان مقدار نسبت شباهت را به‌دست‌آورد. $\ L_{tot}^{free}=\sum _{m=1}^{N}L_{m}^{I}=\sum _{m=1}^{N}[\sum _{i\in \lambda _{m}}\alpha _{t}(i)\mathrm {B} _{t}(i)]\sum _{m=1}^{N}\sum _{i\in \lambda _{i}}\alpha _{T}(i)$

که در آن $\ L_{m}^{I}$ بیانگر میزان شباهت دنبالهٔ مشاهدات فعلی به کلاس l در مدل $\ \lambda _{m}$ است.

شناسایی

در مقایسه با آموزش، روال شناسایی بسیار ساده‌تر است. الگوریتم دنبالهٔ مشاهدات موردنظر را دریافت می‌کند.

$\ I^{*}\ \arg maxL_{m}^{I}$

$\ 1\leq m\leq N$

در این حالت نرخ شناسایی به صورت نسبت بین واحدهای شناسایی صحیح به کل واحدهای آموزشی حساب می‌شود.

منبع

برای دریافت اطلاعات بیشتر فایل زیر را دانلود و مشاهده فرمایید.

رمز فایل: behsanandish.com

ML_93_1_Chap15_Hidden Markov Model

Hidden Markov Model

مدل مخفی مارکوف (Hidden Markov Model) قسمت 1
مدل مخفی مارکوف (Hidden Markov Model) قسمت 2
مدل مخفی مارکوف (Hidden Markov Model) قسمت 3
مدل مخفی مارکوف (Hidden Markov Model) قسمت 4

نوامبر 4, 2019/0 دیدگاه /توسط hgadmin

مدل مخفی مارکوف (Hidden Markov Model) قسمت 3

دسته‌بندی نشده

انواع مدل‌های مخفی مارکوف و HMM پیوسته

همان‌طور که گفته شد نوع خاصی از HMM وجود دارد که در آن تمام حالات موجود با یکدیگر متصل هستند. لیکن مدل مخفی مارکوف از لحاظ ساختار و اصطلاحاً توپولوژی انواع مختلف دارد. همان‌طور که گفته شد برای مدل ارگودیک برای تمام i و jها $\ a_{ij}>0$ است و ساختار مدل مثل یک گفتار کامل است که راسها در آن دارای اتصالات بازگشتی نیز می‌باشند. لیکن برای کاربردهای متفاوت و با توجه به پیچیدگی فرایند نیاز به ساختار متفاوتی وجود دارد. از جمله این ساختارها که به شکل گسترده‌ای در کاربردهای شناسایی گفتار مبتنی بر واج و شناسایی گوینده مورد استفاده قرار می‌گیرد، مدل چپ به راست یا مدل بکیس است. این مدل که ساختار آن را در شکل ۲ نیز می‌بینید، دارای اتصالات چپ به راست است و برای مدل کردن سیگنالهایی که خواص آن‌ها با زمان تغییر می‌کند مورد استفاده قرار می‌گیرد. در مدل چپ به راست تنها یک حالت ورودی وجود دارد که همان حالت اول است و به این ترتیب:

$\pi _{t}={\begin{cases}0,&\,i\neq 1\\1,&\,i\neq 1\end{cases}}$ مدلهای ارگودیک و چپ به راست مدل‌های HMM پایه هستند و در پردازش گفتار نیز بیشترین کاربرد را دارا می‌باشند. هرچند می‌توان با اتصال چندین مدل یا تغییر در ساختار اتصالات آن مدلهایی با انعطاف‌پذیری بیشتری ایجاد نمود. شکل ۲-ج یک نمونه از مدل موازی چپ به راست، که شامل دو مدل چپ به راست است، را نشان می‌دهد.

در قسمت‌های قبل مدل‌های HMM برای مجموعه مشاهدات گسسته را مورد بررسی قرار دادیم. اگر چه می‌توان با چندی‌سازی تمام فرایندهای پیوسته را به فرایندهای با دنباله مشاهدات گسسته تبدیل نمود، اما این کار ممکن است باعث افت مدل شود. در مدل HMM پیوسته احتمال قرار گرفتن مشاهدات در یک حالت را با توابع چگالی احتمال نشان می‌دهند. در این شرایط برای هر حالت i و ورودی O، احتمال مشاهده $\ b_{t}(O)$ به صورت یک توزیع شامل M مخلوط نشان داده می‌شود:

$\ b_{t}(O)=\sum _{m=1}^{M}c_{im}R(O,\mu _{im},U_{im})$

$\ c_{im}\geq 0,1\leq i\leq N,1\leq m\leq M$

مدل مخلوط گاوسی

مدل مخلوط گوسی یکی از مهمترین روش‌های مدل کردن سیگنال است که در واقع شبیه یک HMM یک حالته است که تابع چگالی احتمال آن حالت دارای چندین مخلوط نرمال می‌باشد. احتمال تعلق بردار آزمایشیd به یک مدل مخلوط گاوسی دارای M مخلوط به شکل زیر بیان می‌شود:

$P(x|GMM)=\sum _{t=1}^{M}c_{t}.N(\mu _{t},\Sigma _{t}),$

که در آن $\ c_{t}$ وزن مخلوط $\mu _{t}$ و $\Sigma _{t}$ به ترتیب بردار میانگین و ماتریس کوواریانس توزیع نرمال هستند. ماتریس کوواریانس مدل GMM معمولاً به صورت قطری در نظر گرفته می‌شود، گرچه امکان استفاده از ماتریس کامل نیز وجود دارد.

برای به‌دست آوردن پارامترهای مدل GMM، شامل وزن مخلوط‌های گاوسی و میانگین و کواریانس توزیع‌ها، از الگوریتم ماکزیمم نمودن امید ریاضی(EM)استفاده می‌شود. باید توجه داشت که تعداد مخلوطهای گاوسی با تعداد نمونه‌های موجود آموزشی رابطه مستقیم دارند و نمی‌توان با مجموعه داده‌ای ناچیز یک مدل GMM دارای تعداد بیش از حد از مخلوطها را آموزش داد. در تشکیل و آموزش مدل GMM مانند تمام روش‌های تشکیل مدل رعایت نسبت میزان پیچیدگی مدل و نمونه‌های آموزشی الزامی می‌باشد.

فرضیات تئوری مدل مخفی مارکوف

برای اینکه مدل مخفی مارکوف از لحاظ ریاضی و محاسباتی قابل بیان باشد فرضهای زیر در مورد آن در نظر گرفته می‌شود.

۱- فرض مارکوف

با داشتن یک مدل مخفی مارکوف، احتمال انتقال از حالت i به حالت j به صورت زیر تعریف می‌شود:

$\ a_{ij}=p(q_{t+1}|q_{t}=i)$

به بیان دیگر فرض می‌شود که حالت بعدی تنها به حالت فعلی بستگی دارد. مدل حاصل از فرض مارکوف یک مدل HMM مرتبه صفر می‌باشد. در حالت کلی، حالت بعدی می‌تواند با k حالت قبلی وابسته باشد. این مدل که مدل HMM مرتبه k ام گفته می‌شود، با استفاده از احتمالات انتقال به صورت زیر تعریف می‌گردد.

$\ a_{i1}a_{i2}a_{i3}a{i4}...=p(q_{t+1}=j|q_{t}=i_{1},q_{t-1}=i_{2}....,q_{t-k+1}=i_{k},1\leq i_{1},i_{2},...i_{k},j\leq N))$

به نظر می‌رسد که یک مدل HMM از مرتبه بالاتر باعث افزایش پیچیدگی مدل می‌شود. علی‌رغم اینکه مدل HMM مرتبه اول متداول‌ترین مدل است، برخی تلاشها برای استفاده از مدل‌های دارای مرتبه بالاتر نیز در حال انجام می‌باشد.

۲- فرض ایستایی (stationarity)

در اینجا فرض می‌شود که احتمال انتقال در بین حالات از زمان واقعی رخداد انتقال مستقل است. در این صورت می‌توان برا ی هر $\ t_{1},t_{2}$ نوشت

$\ p(q_{t_{1}+1}=j|q_{t_{1}}=i)=p(q_{t_{2}+1}=j|q_{t_{2}}=i$

۳- فرض استقلال خروجی

در این حالت فرض می‌شود که خروجی (مشاهدات) فعلی به صورت آماری از خروجی قبلی مستقل است. می‌توان این فرض را با داشتن دنباله‌ای از خروجی‌ها مانند بیان نمود:

$\ O=o_{1},o_{2},....o_{T}$

آنگاه مطابق با این فرض برای مدل HMM با نام $\ \lambda$ خواهیم داشت:

$\ p(O|q_{1},q_{2},..q_{T},\lambda )={\begin{matrix}\prod _{t=1}^{T}p(O_{t}|q_{t},\lambda )\end{matrix}}$

اگر چه بر خلاف دو فرض دیگر این فرض اعتبار کمتری دارد. در برخی حالات این فرضیه چندان معتبر نیست و موجب می‌شود که مدل HMM با ضعفهای عمده‌ای مواجه گردد.

مسئله ارزیابی و الگوریتم پیشرو (forward)

در این حالت مسئله این است که با داشتن مدل $\lambda =(A,B,\pi )$ و دنباله مشاهدات $O=\{O_{1},O_{2},...,O_{T}\}$ باید مقدار $\ P(O|\lambda )$ را پیدا نماییم. می‌توانیم این مقدار را با روش‌های آماری مبتنی بر پارامترها محاسبه نماییم. البته این کار به محاسباتی با پیچیدگی $\ O(N^{T})$ احتیاج دارد. این تعداد محاسبات حتی برای مقادیر متوسط t نیز بسیار بزرگ است. به همین دلیل لازم است که راه دیگری برای این محاسبات پیدا نماییم. خوشبختانه روشی ارائه شده‌است که پیچیدگی محاسباتی کمی دارد و از متغیر کمکی $\ a_{t}(i)$ با نام متغیر پیشرو استفاده می‌کند.

متغیر پیشرو به صورت یک احتمال از دنباله مشاهدات $O=\{O_{1},O_{2},...,O_{t}\}$ تعریف می‌شود که در حالت i خاتمه می‌یابد. به بیان ریاضی:

$\alpha _{t}(i)=p\{O_{1},O_{2},...,O_{t},q_{t}=i|\lambda \}$ آنگاه به سادگی مشاهده می‌شود که رابطه بازگشتی زیر برقرار است.

$\ a_{t+1}(j)=b_{j}(O_{t+1}\sum _{i=1}^{N})a_{t}(i)a_{ij},1\leq j\leq N,1\leq t\leq T-1$

که در آن

$\ a_{1}(j)=\pi _{j}b_{j}(O_{1}),1\leq j\leq N$

با داشتن این رابطه بازگشتی می‌توانیم مقدار زیر را محاسبه نماییم.

$\ a_{T}(i),1\leq i\leq N$

و آنگاه احتمال $\ P(O|\lambda )$ به صورت زیر محاسبه خواهد شد:

$p\{O|\lambda \}=\sum _{i=1}^{N}a_{T}(i)$

پیچیدگی محاسباتی روش فوق که به الگوریتم پیشرو معروف است برابر با $\ O(N^{2}T)$ است، که در مقایسه با حالت محاسبه مستقیم که قبلاً گفته شد، و دارای پیچیدگی نمایی بود، بسیار سریعتر است.

روشی مشابه روش فوق را می‌توان با تعیین متغیر پسرو، $\beta _{t}(i)$ ، به عنوان احتمال جزئی دنباله مشاهدات $O=\{O_{t+1},O_{t+2},...,O_{T}\}$ در حالت i تعریف نمود. متغیر پیشرو را می‌توان به شکل زیر نمایش داد.

$\beta _{t}(i)=p\{O_{t+1},O_{t+2},...,O_{T}|q_{t}=i,\lambda \}$

مانند روش پیشرو یک رابطه بازگشتی به شکل زیر برای محاسبه $\beta _{t}(i)$ وجود دارد.

$\beta _{t}(i)=\sum _{i=1}^{N}\beta _{t+1}(j)a_{ij}b_{j}(O_{t+1}),1\leq i\leq N,1\leq t\leq T-1$

که در آن

$\beta _{t}(i)=1,1\leq i\leq N$

می‌توان ثابت کرد که

$\ a_{t}(i)\beta _{t}(i)=p\{O,q_{t}=i|\lambda \},1\leq i\leq N,1\leq t\leq T$

آنگاه می‌توان با کمک هر دو روش پیشرو و پسرو مقدار احتمال $\ P(O|\lambda )$ را محاسبه نمود.

$p\{O|\lambda \}=\sum _{i=1}^{N}p\{O,q_{t}=i|\lambda \}=\sum _{i=1}^{N}a_{t}(i)\beta _{t}(i)$ رابطه فوق بسیار مهم و مفید است و بخصوص برای استخراج روابط آموزش مبتنی بر گرادیان لازم می‌باشد.

نوامبر 3, 2019/0 دیدگاه /توسط hgadmin

مدل مخفی مارکوف (Hidden Markov Model) قسمت 2

دسته‌بندی نشده

کاربردهای مدل مخفی مارکوف

بازشناسی گفتار
ترجمه ماشینی
پیش‌بینی ژن
هم‌ترازسازی توالی
تشخیص فعالیت
تاشدگی پروتئین
تشخیص چهره

تاریخچه

مدل مخفی مارکوف برای اولین بار در مجموعه‌مقالات آماری leonard E.Baum و سایر نویسندگان در نیمه دوم دهه ۱۹۶۰ توضیح داده شد. یکی از اولین کاربردهای HMM تشخیص گفتار بوده که در اواسط دههٔ ۱۹۷۰ شروع شد. HMM در نیمهٔ دوم ۱۹۸۰ وارد حوزهٔ آنالیز دنباله‌های بیولوژیکی، به‌طور خاص DNA شد. از آن پس، کاربرد آن در بیوانفورماتیک گسترش یافت.

انواع مدل مخفی مارکوف

مدل پنهان مارکوف می‌تواند فرایندهای پیچیده مارکوف را که حالتها بر اساس توزیع احتمالی مشاهدات را نتیجه می‌دهند، مدل کند. به‌طور مثال اگر توزیع احتمال گوسین باشد در چنین مدل مارکوف پنهان خروجی حالتها نیز از توزیع گوسین تبعیت می‌کنند. علاوه بر این مدل مخفی مارکوف می‌تواند رفتارهای پیچیده‌تر را نیز مدل کند. جایی که خروجی حالت‌ها از ترکیب دو یا چند توزیع گوسین پیروی کند که در این حالت احتمال تولید یک مشاهده از حاصلضرب گوسین انتخاب شدهٔ اولی در احتمال تولید مشاهده از گوسین دیگر به دست می‌آید.

فرایند مارکوف گسسته

یک سیستم مانند شکل زیر را که در هر لحظه در یکی از حالت متمایز S1,… ,SN است در نظر بگیرید. در زمان‌های گسسته و با فواصل منظم، حالت سیستم با توجه به مجموعه‌ای از احتمالات تغییر می‌کند. برای زمان‌های… ,t=۱٬۲ حالت در لحظه t را با qt نشان می‌دهیم. برای یک توصیف مناسب از سیستم فعلی نیاز به دانستن حالت فعلی در کنار تمام حالات قبلی می‌باشد. برای یک حالت خاص از زنجیره مارکوف مرتبه اول، توصیف احتمالاتی تنها با حالت فعلی و حالت قبلی مشخص می‌شود.

\ P(q_{t}=S_{j}|q_{t-1}=S_{i},q_{t-2}=S_{k},...)=

\ P(q_{t}=S_{j}|q_{t-1}=S_{i})

حال تنها فرایندهایی را در نظر می‌گیریم که در آن‌ها سمت راست رابطه فوق مستقل از زمان است و به همین دلیل ما مجموعه‌ای از احتمالات انتقال بین حالت‌ها را خواهیم داشت.

$\ a_{ij}=P(q_{t}=S_{j}|q_{t-1}=S_{i})\qquad i\geq 1,N\geq j$

که در آن احتمال انتقال بین حالات دارای خواص زیر است.

$a_{ij}\geq 0$

$\sum _{j=1}^{N}a_{ij}=1$

فرایند تصادفی فوق را مدل مارکوف قابل مشاهده می‌گویند زیرا خروجی مدل مجموعه‌ای از حالات است که قرار گرفتن در آن‌ها متناظر با یک مشاهده می‌باشد. ما می‌توانیم دنباله مشاهدات مورد انتظار خود را تولید کنیم و احتمال وقوع آن در زنجیره مارکوف را محاسبه نماییم. برای مثال با داشتن دنباله مشاهدات $\ O={q_{1},...,q_{t}}$ احتمال وقوع آن به صورت زیر بیان می‌شود.

$\ P(O|Model)=P({q_{1},q_{2},...,q_{2}}|Model)$

$\ P(q_{1}).P(q_{2}|q_{1}).P(q_{3}|q_{2})...P(q_{t}|q_{t-1})$

یکی دیگر از مواردی که مطرح می‌شود این است که اگر سیستم در حالت $\ q_{i}$ باشد با چه احتمالی به حالت $\ q_{j}$ می‌رود و با چه احتمالی در همان حالت $\ q_{i}$ باقی می‌ماند.

مرتبه مدل مارکوف

۱- مدل مارکوف مرتبه صفر

یک مدل مارکوف از مرتبه صفر هیچ حافظه‌ای ندارد و برای هر t و t’ در دنباله سمبل‌ها، $\ pr(X_{t}=S_{i})=pr(X_{t'}=S_{i})$ خواهد بود. مدل مارکوف از مرتبه صفر مانند یک توزیع احتمال چند جمله‌ای می‌باشد.

۲- مدل مارکوف مرتبه اول

یک مدل مارکوف مرتبه اول دارای حافظه‌ای با طول ۱ می‌باشد. توزیع احتمال در این مدل به صورت زیر مشخص می‌شود.

$\ pr(X_{t}=S_{i}|X_{t-1}=S_{j}),fori=1..k,j=1..k$

تعریف فوق مانند این است که k مدل مارکوف در مرتبه صفر برای هر $\ S_{j}$ داشته باشیم.

۳- مدل مارکوف مرتبه m ام

مرتبه یک مدل مارکوف برابر است با طول حافظه‌ای که مقادیر احتمال ممکن برای حالت بعدی به کمک آن محاسبه می‌شود. برای مثال، حالت بعدی در یک مدل مارکوف از درجه ۲ (مدل مارکوف مرتبه دوم) به دو حالت قبلی آن بستگی دارد.

مثال ۱: برای مثال اگر یک سکه معیوب A داشته باشیم که احتمالات شیر یا خط آمدن برای آن یکسان نباشد، می‌توان آن را با یک مدل مارکوف درجه صفر با استفاده از احتمالات (pr(H و (pr(H توصیف نمود.

pr(H)=0.6, pr(T)=۰٫۴

مثال ۲: حال فرض کنید که سه سکه با شرایط فوق در اختیار داریم. سکه‌ها را با اسامی B, A و C نام‌گذاری می‌نماییم. آنگاه برای توصیف روال زیر به یک مدل مارکوف مرتبه اول نیاز داریم:

فرض کنید سکه X یکی از سکه‌های A یا B باشد.
مراحل زیر را تکرار می‌کنیم.

a) سکه X را پرتاب می‌کنیم و نتیجه را می‌نویسیم.

b) سکه C را نیز پرتاب می‌کنیم.

c) اگر سکه C خط آمد، آنگاه سکه X را تغییر می‌دهیم (A را با B یا B را با A جایگزین می‌کنیم) و در غیر این صورت تغییری در سکه‌ها نمی‌دهیم.

انجام روال فوق مدل مارکوف مرتبه اول زیر را نتیجه خواهد داد.

یک پردازش مارکوفی مانند نمونه فوق در طول پیمایش احتمالات، یک خروجی نیز خواهد داشت. یک خروجی نمونه برای پردازش فوق می‌تواند به شکل HTHHTHHttthtttHHTHHHHtthtthttht باشد.

مدل مارکوف فوق را می‌توان به صورت نموداری از حالات و انتقال‌ها نیز نشان داد. کاملاً مشخص است که این‌گونه بازنمایی از مدل مارکوف مانند بازنمایی یک ماشین انتقال حالت محدود است که هر انتقال با یک احتمال همراه می‌باشد

مدل مخفی مارکوف (HMM)

تا اینجا ما مدل مارکوف، که در آن هر حالت متناظر با یک رویداد قابل مشاهده بود را معرفی نمودیم. در این بخش تعریف فوق را گسترش می‌دهیم، به این صورت که در آن، مشاهدات توابع احتمالاتی از حالتها هستند. در این صورت مدل حاصل یک مدل تصادفی با یک فرایند تصادفی زیرین است که پنهان است و تنها توسط مجموعه‌ای از فرایندهای تصادفی که دنباله مشاهدات را تولید می‌کنند قابل مشاهده است.

برای مثال فرض کنید که شما در یک اتاق هستید و در اتاق مجاور آن فرد دیگری سکه‌هایی را به هوا پرتاب می‌کند و بدون اینکه به شما بگوید این کار را چگونه انجام می‌دهد و تنها نتایج را به اطلاع شما می‌رساند. در این حالت شما با فرایند پنهان انداختن سکه‌ها و با دنباله‌ای از مشاهدات شیر یا خط مواجه هستید. مسئله‌ای که اینجا مطرح می‌شود چگونگی ساختن مدل مارکوف به منظور بیان این فرایند تصادفی است. برای مثال اگر تنها مشاهدات حاصل از انداختن یک سکه باشد، می‌توان با یک مدل دو حالته مسئله را بررسی نمود. یک مدل مخفی مارکوف را می‌توان با تعیین پارامترهای زیر ایجاد نمود:

تعداد حالات ممکن: تعداد حالتها در موفقیت مدل نقش به سزایی دارد و در یک مدل مخفی مارکوف هر حالت با یک رویداد متناظر است. برای اتصال حالتها روش‌های متفاوتی وجود دارد که در عمومی‌ترین شکل تمام حالتها به یکدیگر متصل می‌شوند و از یکدیگر قابل دسترسی می‌باشند. تعداد مشاهدات در هر حالت: تعداد مشاهدات برابر است با تعداد خروجیهایی که سیستم مدل شده خواهد داشت.

N تعداد حالتهای مدل M تعداد سمبلهای مشاهده در الفبا، اگر مشاهدات گسسته باشند آنگاه M یک مقدار نا محدود خواهد داشت.

$\ A={a_{ij}}$

$\ A=[a_{ij}]$ ماتریس انتقال حالت:یک مجموعه از احتمالات در بین حالت‌ها

$\ a_{ij}=p(q_{t+1}=j|q_{t}=i),\qquad i\geq 1,N\geq j$

که در آن $\ q_{t}$ بیانگر حالت فعلی می‌باشد. احتمالات انتقال باید محدودیتها طبیعی یک توزیع احتمال تصادفی را برآورده نمایند. این محدودیتها شامل موارد زیر می‌گردند

$\ a_{ij}\geq 0,\qquad i\geq 1,N\geq j$

$\sum _{j=1}^{N}a_{ij}=1,\qquad 1\leq i\leq N$

برای حالات مدل ارگودیک برای تمامi وjها مقدار $\ a_{ij}$ بزرگتر از صفر است و در موردی که اتصالی بین حالات وجود ندارد $\ a_{ij}=0$ است.

توزیع احتمال مشاهدات: یک توزیع احتمال برای هر یک از حالتها

$\ B={b_{j}(k)}$

$\ b_{j}(k)=p{o_{t}=v_{k}|q_{t}=j},\qquad 1\leq j\leq N,\qquad 1\leq k\leq M$

که در آن $\ v_{k}$ بیانگرkامین سمبل مشاهده شده در الفبا است و $\ o_{t}$ بیانگر بردار پارامترهای ورودی فعلی می‌باشد. در مورد مقادیر احتمال حالتها نیز شرایط موجود در نظریه احتمال باید رعایت گردند.

$\ b_{j}(k)\qquad 1\leq j\leq N,\qquad 1\leq K\leq M$

$\sum _{K=1}^{M}b_{j}(k)=1,\qquad 1\leq j\leq N$

اگر مشاهدات به صورت پیوسته باشند، باید به جای احتمالهای گسسته از یک تابع چگالی احتمال پیوسته استفاده شود. معمولاً چگالی احتمال به کمک یک مجموع وزندار از M توزیع نرمال μ تخمین زده می‌شود.

$\ b_{j}(o_{t})=\Sigma _{m=1}^{M}c_{jm}\mu (\mu _{jm},\Sigma _{jm},o_{t})$

که در آن $\ \mu _{jm}$ ، $\ C_{jm}$ , $\ \Sigma _{jm}$ , به ترتیب ضریب بردار میانگین، ضریب وزندهی و ماتریس کواریانس می‌باشند. در رابطه فوق مقادیر $\ c_{jm}$ باید شرایط زیر را ارضا نماید:

$\ c_{jm},\qquad 1\leq j\leq N,\qquad 1\leq m\leq M$

$\sum _{m=1}^{M}c_{jm}(k)=1,\qquad j\geq 1,N\geq j$

توزیع احتمال حالت آغازین

$\ \pi =(\pi _{i})$ که در آن

$\ \pi _{i}=p(q_{1}=i),\qquad 1\leq i\leq N$

به این ترتیب ما می‌توانیم یک مدل مخفی مارکوف با توزیع احتمال گسسته را با استفاده از سه‌گانه زیر مشخص نماییم.

$\ \lambda =(\mathrm {A} ,\mathrm {B} ,\pi )$

همچنین یک مدل مخفی مارکوف با توزیع احتمال پیوسته به صورت زیر نشان داده می‌شود.

$\ \lambda =(\mathrm {A} ,C_{jm},\mu _{jm},\Sigma _{jm},\pi )$

نوامبر 3, 2019/0 دیدگاه /توسط hgadmin

مدل مخفی مارکوف (Hidden Markov Model) قسمت 1

آموزش عمومی پردازش تصویر و بینایی ماشین

مدل مخفی مارکوف (به انگلیسی: Hidden Markov Model) یک مدل مارکوف آماری است که در آن سیستم مدل شده به صورت یک فرایند مارکوف با حالت‌های مشاهده نشده (پنهان) فرض می‌شود. یک مدل پنهان مارکوف می‌تواند به عنوان ساده‌ترین شبکه بیزی پویا در نظر گرفته شود.

در مدل عادی مارکوف، حالت به‌طور مستقیم توسط ناظر قابل مشاهده است و بنابراین احتمال‌های انتقال بین حالت‌ها تنها پارامترهای موجود است. در یک مدل مخفی مارکوف، حالت به‌طور مستقیم قابل مشاهده نیست، اما خروجی، بسته به حالت، قابل مشاهده است. هر حالت یک توزیع احتمال روی سمبل‌های خروجی ممکن دارد؛ بنابراین دنبالهٔ سمبل‌های تولید شده توسط یک مدل مخفی مارکوف اطلاعاتی دربارهٔ دنبالهٔ حالت‌ها می‌دهد. توجه داشته باشید که صفت ‘پنهان’ به دنبالهٔ حالت‌هایی که مدل از آن‌ها عبور می‌کند اشاره دارد، نه به پارامترهای مدل؛ حتی اگر پارامترهای مدل به‌طور دقیق مشخص باشند، مدل همچنان ‘پنهان’ است.

مدل‌های مخفی مارکوف بیشتر به‌دلیل کاربردشان در بازشناخت الگو، مانند تشخیص صدا و دست‌خط، تشخیص اشاره و حرکت، برچسب‌گذاری اجزای سخن، بیوانفورماتیک و … شناخته‌شده هستند.

مثالی از پارامترهای احتمالاتی یک مدل مخفی مارکوف
x — حالت‌ها
y — مشاهده‌های ممکن
a — احتمال‌های انتقال بین حالت‌ها
b — احتمال‌های خروجی‌ها

شرح ازنظر مسائل ظرف‌ها

مدل مخفی مارکوف در حالت گسسته جز خانوادهٔ مسائل ظرف‌ها قرار می‌گیرد. به‌طور مثال از ربینر ۱۹۸۹: ظروف x1،x2،x3… و توپهای رنگی y1,y2,y3… را در نظر می‌گیریم، که نفر مقابل دنباله‌ای از توپ‌ها را مشاهده کرده ولی اطلاعی از دنبالهٔ ظرف‌هایی که توپ‌ها از آن‌ها انتخاب‌شده ندارد. ظرف n ام با احتمالی وابسته به ظرف n-1 ام انتخاب می‌شود و چون به انتخاب ظرف‌های خیلی قبل‌تر وابسته نیست یک فرایند مارکوف است.

معماری مدل مخفی مارکوف

شکل زیر معماری کلی یک نمونه HMM را نشان می‌دهد. هر شکل بیضی یک متغیر تصادفی است که می‌تواند هر عددی از مقادیر را انتخاب کند. متغیر تصادفی $x(t)$ یک حالت پنهان در زمان t و متغیر تصادفی $y(t)$ مشاهده در زمان $t$ است. فلش‌ها به معنای وابستگی‌های شرطی می‌باشند. از شکل مشخص است که توزیع احتمال شرطی متغیر پنهان $x(t)$ ، در همهٔ زمان هایt مقداری را برای x ارائه می‌دهد که فقط به مقدار متغیر پنهان $x(t-1)$ وابسته است: مقادیر در زمان‌های t-2 و قبل‌تر از آن هیچ اثری ندارند. این مشخصهٔ مارکف نامیده می‌شود. به‌طور مشابه، مقدار متغیر مشاهده‌ای $y(t)$ تنها به مقدار متغیر پنهان $x(t)$ (هر دو در زمان خاص t) بستگی دارد. 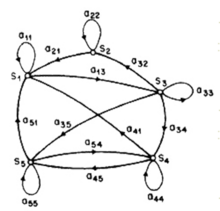در حالت استاندارد مدل مخفی مارکوف که در اینجا در نظر گرفته شده‌است، فضای حالت متغیرهای پنهان گسسته است؛ درحالی‌که متغیرهای مشاهده‌ای می‌توانند گسسته یا پیوسته (از توزیع گوسین) باشند.

در مدل مخفی مارکوف دو نوع پارامتر وجود دارد:احتمال جابه‌جایی‌ها (بین حالات) و احتمال خروجی‌ها (یا مشاهدات). احتمال جابه‌جایی نحوهٔ انتقال از حالت t-1 به t را کنترل می‌کند.

فضای حالت پنهان شامل N مقدار ممکن برای حالات است. متغیر پنهان در زمان t می‌تواند هر یک از این مقادیر را اختیار کند. احتمال جابجایی احتمال این است که در زمان t در حالت k (یکی از حالات ممکن) و در زمان t+1 در حالت k1 باشیم. بنابرین در کل $N^{2}$ احتمال جابجایی وجود دارد. (مجموع احتمالات جابجایی از یک حالت به تمام حالتهای دیگر ۱ است)

احتمال خروجی، احتمال رخ دادن هر یک از اعضای مجموعهٔ مشاهده‌ای را برای هر حالت پنهان ممکنه مشخص می‌سازد که می‌تواند از یک توزیع احتمال پیروی کند. تعداد اعضای مجموعهٔ مشاهده‌ای بستگی به طبیعت متغیر مشاهده‌ای دارد.

اگر تعداد اعضای مجموعهٔ متغیرهای مشاهده‌ای برابر M باشد، بنابراین مجموع تعداد احتمالات خروجی NM می‌باشد/

مسایلی که به کمک مدل مخفی مارکوف حل می‌شود

با توجه به پارامترهای مدل مخفی مارکوف، می‌توانیم مسایلی به صورت زیر را حل کنیم.

Annotation: مدل را داریم به این معنی که احتمالات مربوط به انتقال از حالتی به حالت دیگر و همین‌طور احتمال تولید الفبا در هر حالت معلوم است. توالی از مشاهدات داده شده، می‌خواهیم محتمل‌ترین مسیری (توالی حالات) که توالی را تولید می‌کند را پیدا کنیم. الگوریتم viterbi می‌تواند این‌گونه مسایل را به صورت پویا (Dynamic) حل کند.
classification: مدل را داریم، توالی از مشاهدات داده شده‌است، می‌خواهیم احتمال (کل) تولید شدن این توالی توسط این مدل را (جمع احتمالات تمامی مسیرهایی که این توالی را تولید می‌کنند) حساب کنیم. الگوریتم forward
Consensus: مدل را داریم، می‌خواهیم بدانیم محتمل‌ترین توالی که توسط این مدل تولید می‌شود (توالی که بیشترین احتمال را داراست) چیست. الگوریتم Backward
Training: ساختار مدل را داریم به این معنی که تعداد حالات و الفبای تولیدی در هر حالت معلوم است، تعدادی توالی داریم (داده‌های آموزش) می‌خواهیم احتمال انتقال بین حالات و همین‌طور احتمال تولید الفبا در هر حالت را محاسبه کنیم. الگوریتم Baum-Welch

یادگیری

وظیفه یادگیری در HMM، یافتن بهترین احتمالات جابجایی‌ها و خروجی‌ها بر اساس یک دنباله یا دنباله‌هایی از خروجی هاست. معمولاً این پارامترها به وسیله متد maximum likelihood بر اساس خروجی داده شده تخمین زده می‌شوند. هیچ الگوریتم قطعی برای حل این مسئله وجود ندارد ولی برای پیدا کردن maximum likelihood محلی می‌توان از الگوریتم‌های کارایی مانند Baum-welch algorithmو یا Baldi-chauvin algorithmاستفاده کرد. الگوریتم Baum-Welch نمونه‌ای از الگوریتم forward-backwardو به صورت خاص موردی از الگوریتم exception-maximization می‌باشد.

یک مثال ملموس

دو دوست به نام‌های آلیس و باب را در نظر بگیرید. آن‌ها دور از هم زندگی کرده و هر روز دربارهٔ کارهای روزمره‌شان با هم تلفنی صحبت می‌کنند. فعالیت‌های باب شامل “قدم زدن در پارک”،”خرید کردن” و “تمیز کردن آپارتمان” می‌شود. انتخاب اینکه هر روز کدام کار را انجام دهد منحصراً بستگی به هوای همان روز دارد. آلیس اطلاع دقیقی از هوای محل زندگی باب نداشته ولی از تمایلات کلی وی آگاه است (بنا به نوع هوا چه کاری را دوست دارد انجام دهد). بر اساس گفته‌های باب در پایان هر روز، آلیس سعی می‌کند هوای آن روز را حدس بزند. آلیس هوا را یک زنجیرهٔ گسستهٔ مارکوف می‌پندارد که دو حالت “بارانی” و “آفتابی” دارد. اما به‌طور مستقیم هوا را مشاهده نمی‌کند؛ بنابراین، حالات هوا بر او پنهان است. در هر روز احتمال اینکه باب به “قدم زدن”،”خرید کردن” و “تمیز کردن”بپردازد بستگی به هوا داشته و دارای یک احتمال مشخص است. مشاهدات مسئله شرح فعالیت‌هایی است که باب در انتهای هر روز به آلیس می‌گوید.

آلیس اطلاعات کلی دربارهٔ هوای محل زندگی باب و اینکه در هر نوع آب و هوا با چه احتمالی چه کار انجام می‌دهد را دارد. به عبارت دیگر پارامترهای مسئله HMM معلوم هستند که در کد زیر مشاهده می‌شوند:

states = ('Rainy', 'Sunny')

observations = ('walk', 'shop', 'clean')

start_probability = {'Rainy': 0.6, 'Sunny': 0.4}

transition_probability = {
   'Rainy': {'Rainy': 0.7, 'Sunny': 0.3},
   'Sunny': {'Rainy': 0.4, 'Sunny': 0.6},
  }

emission_probability = {
   'Rainy': {'walk': 0.1, 'shop': 0.4, 'clean': 0.5},
   'Sunny': {'walk': 0.6, 'shop': 0.3, 'clean': 0.1},
  }

در این کد start_probability نمایانگر احتمال رخ دادن هر یک از حالات HMM (بارانی یا آفتابی) در روز اولی که باب با آلیس صحبت می‌کند می‌باشد.transition_probability نمایانگر تغییر هوا بر اساس قواعد زنجیرهٔ مارکو است. به‌طور مثال اگر امروز بارانی باشد به احتمال ۳۰٪فردا آفتابی است.emition_probability نمایانگر این است که باب علاقه دارد که در هر هوایی چه کار کند به‌طور مثال در هوای بارانی با احتمال ۵۰٪ آپارتمانش را تمیز کرده یا در هوای آفتابی با احتمال ۶۰٪در پارک قدم می‌زند.

مدل مخفی مارکوف (Hidden Markov Model) قسمت 1

مدل مخفی مارکوف (Hidden Markov Model) قسمت 2

مدل مخفی مارکوف (Hidden Markov Model) قسمت 3

مدل مخفی مارکوف (Hidden Markov Model) قسمت 4

نوامبر 2, 2019/0 دیدگاه /توسط daliri

ارائه الگوریتمی جدید برای حذف نویز از تصاویر دیجیتالی با استفاده از شبکه های عصبی و فیلتر میانی:

پردازش تصویر

انواع تصاویر دیجیتال

تصاویر دودویی

تصاویر شدت روشنایی

تصاویر رنگی

تصاویر شاخص

الگوریتم مبتنی بر تصمیم گیری

متدهای مبتنی بر محاسبات نرم

نویز چیست ؟

طیف نویز

انواع نویز

نویز حرارتی

نویز فلیکر

نویز چیست ؟

نویز در دوربین‌های مداربسته

نویز در شبکه‌های رایانه‌ای

حرارت

القای الکترومغناطیسی

هم‌شنوایی

انواع نویز :

نویز دمایی :

نویز یا اثر ساچمه ای (Shot noise)

نویز ۱/f (نویز صورتی)

معرفی EMG:

سیستم استنتاج فازی (Fuzzy Inference Systems (FIS

ممداني، سوگنو، لارسن و تاكاگی

انواع سیستم های استنتاج فازی (1) (ممدانی)

انواع سیستم های استنتاج فازی (2)

مدل Sugeno

تکنیک های استنتاج فازی

گریزی بر شبکه های عصبی

دو نوع الگوریتم یادگیری در شبکه های عصبی

سیستم های فازی و شبکه های عصبی

ANFIS

معرفی ANFISS

مقدمه

مزایا و معایب منطق فازی

سيستم های استنتاج فازی

کاربردهای سيستم استنتاج فازی

انواع الگوریتم های استنتاج فازی

1-الگوریتم استنتاج ممدانی

2- الگوریتم استنتاج تاکاگی سوگنو

مقایسه الگوریتم استنتاج فازی ممدانی و سوگنو

نتيجه گيری

سيستم استنتاج فازي

تعریف متغیر ها

تعریف توابع عضویت

تعریف rule ها

بررسی

اصلاح دیجیتالی عکس در دوربین

اندازه عکس

کیفیت عکس

وضوح عکس

تعادل نور سفید

حالت رنگ

حساسیت به نور

کار روی عکسها درون دوربین

ذخیره عکسها در پوشه های مختلف

تنظیم نامگذاری عکسها

حذف کردن عکسها

دوربین های دیجیتال:

تاریخچه:

عملکرد:

سنسورهای CCD و CMOS

تفاوت دیجیتال و آنالوگ چیست؟

تصاویر رنگی در دوربین های دیجیتال:

منابع

مسئله کد گشایی و الگوریتم ویتربی (Viterbi Algorithm)

مسئله یادگیری

معیار بیشترین شباهت((Maximum Likelihood (ML)

الگوریتم بام- ولش

الگوریتم حداکثرسازی امید ریاضی (Expectation Maximization)

روش مبتنی بر گرادیان

استفاده از مدل HMM در شناسایی گفتار

استفاده از HMM در شناسایی کلمات جداگانه

آموزش

شناسایی

انواع مدل‌های مخفی مارکوف و HMM پیوسته

مدل مخلوط گاوسی