زنجیره مارکوف (Markov Approach modeling) قسمت 4

زنجیره ارگودیک و زنجیره باقاعده

یک زنجیره مارکوف ارگودیک است ا اگر بتوان با تعدادی حرکت از هر حالتی به حالت دیگر رسید. زنجیره ارگودیک زنجیره تقلیل‌ناپذیر نیز نامیده می‌شود. زنجیره‌ای که هم تقلیل‌ناپذیر باشد و هم غیر متناوب، زنجیره باقاعده (regular) نامیده می‌شود. به عبارت دیگر زنجیره‌ای با قاعده است که تقلیل‌ناپذیر باشد و هر حالت آن نامتناوب و بازگشتی مثبت باشد. در زنجیره باقاعده n ای وجود دارد که اگر ماتریس انتقال حالت به توان n برسد تمام درایه‌های آن مثبت خواهند بود. بدین معنا که با n حرکت می‌توان از هر حالتی به حالت دیگر رسید.

متوسط زمان اصابت

در یک زنجیره ارگودیک زمان اولین بار رسیدن یا اصابت به حالت j در حالی که زنجیر مارکوف در حالت i بوده‌است، زمان اصابت از i به j نامیده می‌شود. زمان اصابت با متغیر تصادفی $T_{ij}$ به صورت زیر توصیف می‌شود:

$T_{ij}=\inf\{n\geq 1:X_{n}=j|X_{0}=i\}.$

متوسط زمان اصابت از i به j، یعنی $H_{ij}=E[T_{ij}]$ ، از رابطهٔ بازگشتی زیر بدست می‌آید:

H_{ij}=\sum _{r\in S}p_{ir}H_{rj}

تجزیه و تحلیل توزیع ثابت و محدود کردن توزیع‌ها

برای یک زنجیر یکنواخت در زمان، بردار ${\boldsymbol {\pi }}$ یک «توزیع ثابت» (یا ایستا) نامیده می‌شود اگر $\pi _{j}$ ‌ها نامنفی و جمع آن‌ها برابر ۱ شود و نیز در رابطه زیر صدق کنند:

$\pi _{j}=\sum _{i\in S}\pi _{i}p_{ij}.$

یک زنجیره ارگودیک یک توزیع ثابت دارد اگر و فقط اگر همه حالت‌های آن مثبت باشند در این صورت π یکتاست و مربوط به زمان بازگشت مورد انتظار است:

$\pi _{j}={\frac {1}{M_{j}}}.\,$

اگر زنجیره باقاعده (غیر تقلیل پذیر و غیر متناوب) باشد آن گاه برای هر i و j داریم:

$\lim _{n\rightarrow \infty }p_{ij}^{(n)}={\frac {1}{M_{j}}}.$

لازم است ذکر شود که هیچ شرطی روی نقطه شروع توزیع وجود ندارد یعنی زنجیره صرف نظر از نقطه شروع به توزیع ثابت میل می‌کند. این π «توزیع تعادل» زنجیره نامیده می‌شود. اگر زنجیره بیش از یک کلاس مرتبط بسته داشته باشد توزیع ثابت آن یکتا نخواهد بود. زنجیره غیر یکنواخت در زمان نیز می‌تواند توزیع تعادل داشته باشد.

در هر صورت اگر حالت j ام غیر متناوب باشد آن گاه:

$\lim _{n\rightarrow \infty }p_{jj}^{(n)}={\frac {1}{M_{j}}}$

و برای هر حالت i دیگر اگر f_ij احتمال این باشد که زنجیره در حالت j قرار گیرد در صورتی که شروع زنجیره از حالت i باشد خواهیم داشت:

$\lim _{n\rightarrow \infty }p_{ij}^{(n)}={\frac {f_{ij}}{M_{j}}}.$

اگر حالت i متناوب باشد با دوره تناوب k > 1 آنگاه حد

$\lim _{n\rightarrow \infty }p_{ii}^{(n)}$

وجود ندارد و نیز حد

$\lim _{n\rightarrow \infty }p_{ii}^{(kn+r)}$

برای هر r صحیح وجود ندارد.

زنجیره وارون پذیر

یک زنجیره مارکوف وارون پذیر نامیده می‌شود اگر یک توزیع احتمال $\pi$ بر روی حالتها وجود داشته باشد به‌طوری‌که برای تمام زمان‌های n و حالتهای i و j رابطهٔ زیر برقرار باشد:

$\pi _{i}\Pr(X_{n+1}=j\mid X_{n}=i)=\pi _{j}\Pr(X_{n+1}=i\mid X_{n}=j)$

برای زنجیره‌های یکنواخت در زمان رابطهٔ بالا به صورت سادهٔ زیر نوشته می‌شود:

\pi _{i}p_{ij}=\pi _{j}p_{ji}\,.

توزیع احتمال $\pi$ در رابطهٔ بالا همان توزیع ثابت در زنجیره‌های ارگودیک می‌باشد.

کاربردها

فیزیک

سیستم‌های مارکوفی در ترمودینامیک و مکانیک آماری بسیار ظاهر می‌شوند، جایی که احتمال برای نشان دادن ویژگی‌های ناشناخته سیستم به کار می‌رود، اگر بتوان فرض کرد که دینامیک مستقل از زمان است و احتیاجی به بررسی پیشینه تاریخی آن نیست. مسیرها، در فرمول انتگرال مسیر مکانیک کوانتومی، زنجیره مارکوف هستند. همچنین زنجیر مارکوف در شبیه‌سازی شبکهای QCD استفاده می‌شود.

علم اطلاعات

زنجیره مارکوف در نظریه اطلاعات کاربرد دارد. مقاله معروف کلود شانون در سال ۱۹۴۸ با «نظریه ریاضی ارتباطات» که پایه‌گذار نظریه اطلاعات شد با معرفی آنتروپی از طریق مدل‌سازی مارکوف از زبان انگلیسی آغاز می‌شود. چنین مدل‌های ایده‌آلی بسیاری از قواعد آماری سیستم را به دست می‌دهند. حتی بدون داشتن ساختار کامل سیستم این گونه مدل‌سازی‌ها فشرده سازی مؤثر داده‌ها را ممکن می‌سازند.

زنجیره‌های مارکوف پایه و اساس مدل پنهان مارکوف است که این مدل یکی از ابزارهای مهم در زمینه‌های گوناگون مثل شبکه‌های تلفن (برای تصحیح خطا)، تشخیص گفتار و هم چنین بیوانفورماتیکاست.

نظریه صف

زنجیره‌های مارکوف اساس رفتار تحلیلی صف ها(نظریه صف) می‌باشد و این امر وجود آن‌ها را برای بهینه‌سازی عملکرد شبکه‌های مخابراتی حیاتی می‌سازد. جایی که پیام‌ها برای منابع محدود (مانند پهنای باند) رقابت می‌کنند. مدل‌های صف بندی بسیاری از زنجیره مارکوف زمان پیوسته استفاده می‌کنند. برای مثال، یک صف M / M / 1 یک CTMC بر روی عدد صحیح غیر منفی است که در آن انتقال از i به i + 1 بر اساس یک فرایند پوآسون با نرخ λ رخ می‌دهد و ورود کار را توصیف می‌کند، در حالی که انتقال از i به i – 1 (برای i> 1) در نرخ μ اتفاق می‌افتد (بار خدمات شغلی از توزیع نمایی پیروی می‌کنند) و خدمات کامل یا همان خروج از صف را نشان می‌دهد.

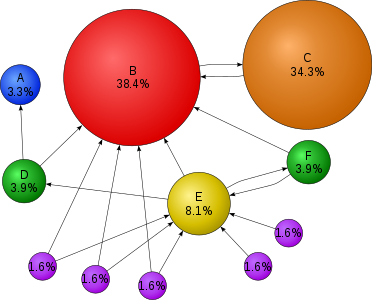
نمایش سادهٔ شبکه‌ای از چند صفحه که با رتبه صفحه ارزیابی شده‌اند.

کاربرد اینترنتی

یکی از نتایج جالب از زنجیرهٔ مارکوف این است که با افزایش طول زنجیر (افزایش تعداد تغییر حالات)، احتمال رسیدن به یک حالت خاص به عددی ثابت همگرا خواهد شد. اکنون تمام شبکه جهانی وب را یک زنجیره مارکوف در نظر بگیرید که در آن هر صفحه یک حالت و پیوند میان آنان احتمال هر تغییر حالت را مشخص می‌کند. این نظریه می‌گوید مستقل از صفحه‌ای که از آن شروع کرده‌ایم، پس از مدتی طولانی گشتن در وب احتمال رسیدن به صفحه‌ای خاص مقدار ثابتی دارد. با این مدل‌سازی می‌توان گفت هر چه احتمال رسیدن به یک صفحه بیشتر باشد، آن صفحه از اهمیت بالاتری برخوردار است.

رتبه صفحه (Page Rank)، برای یک صفحهٔ وب که گوگل نیز از آن استفاده کرده‌است، توسط یک زنجیره مارکوف تعریف شده‌است. همچنین مدل مارکوف برای تحلیل رفتارهای وب کاربران و سیر حرکت آن‌ها میان صفحات استفاده شده‌است. انتقال کاربر به یک صفحه وب خاص از طریق یک لینک می‌تواند با استفاده از مدل‌های مارکوف مرتبه اول یا دوم مدل شود و برای پیش‌بینی‌های مربوط به حرکات آینده و شخصی‌سازی وب برای کاربر مورد استفاده قرار گیرد.

منبع

زنجیره مارکوف یک مفهوم ساده است که توانایی بیان اغلب فرآیندهای پیچیده بلادرنگ را دارد. حوزه هایی مانند بازشناسی صدا، شناسایی متن و بسیاری از حوزه های هوش مصنوعی، به نحوی از این اصل ساده استفاده می کنند. در این مقاله به شرح این مفهوم پرداخته ایم .

زنجیره مارکوف بر اصل بدون یادآوری یا بی حافظه بنا شده است به این معنی که حالت بعدی سیستم، به حالت های قبلی آن بستگی ندارد. با این اصل، محاسبه احتمال عملیات مجاز بعدی بسیار ساده تر خواهد بود. البته حالت پیشرفته تری از زنجیره مارکوف با نام Latent MC در کاربردهای دنیای واقعی که وابستگی به عملیات قبلی هم جزء الزامات پیش بینی ها خواهد بود، استفاده میشود که در اینجا به آن نمی پردازیم.

یک مثال عملی

فرض کنید دو شرکت Coke و Pepsi تنها شرکتهای تولید کننده یک ماده غذایی در کشور X هستند، شرکت Y قصد انتخاب یک شریک تجاری از بین این دو رقیب را دارد. آنها از یک شرکت تحلیلگر بازار خواسته اند که شرایط بازار را برای هر دو برند بررسی کند .شرکتی که بعد از یکماه بیشترین سهم بازار را داشته باشد، برنده این شراکت خواهد بود .

شرکت تحلیل گر نتایج زیر را بعد از بررسی بازار ارائه داده است :

P(P->P) = 0.7 – احتمال ماندن مشتریان برند Pepsi بعد از یکماه با برند Pepsi

P(P->C) = 0.3 – احتمال تغییر شرکت مشتریان Pepsi بعد از یکماه به برند Coke

P(C->C) = 0.9 – حتمال ماندن مشتریان برند Coke بعد از یکماه با برند Coke

P(C->P) = 0.1 – حتمال تغییر شرکت مشتریان Coke بعد از یکماه به برند Pepsi

همانطور که می بینید مشتریان شرکت Coke وفادارترند اما سهم بازار این شرکت در حال حاضر کمتر است . برای تصمیم گیری نهایی بهتر است محاسبات اندکی انجام دهیم و آینده را پیش بینی کنیم که کدام شرکت برنده بازار خواهد بود ؟

زنجیره مارکوف (Markov Approach modeling) قسمت 1
زنجیره مارکوف (Markov Approach modeling) قسمت 2
زنجیره مارکوف (Markov Approach modeling) قسمت 3
زنجیره مارکوف (Markov Approach modeling) قسمت 4
زنجیره مارکوف (Markov Approach modeling) قسمت 5

زنجیره مارکوف (Markov Approach modeling) قسمت 4

زنجیره ارگودیک و زنجیره باقاعده

متوسط زمان اصابت

تجزیه و تحلیل توزیع ثابت و محدود کردن توزیع‌ها

زنجیره وارون پذیر

کاربردها

فیزیک

علم اطلاعات

نظریه صف

کاربرد اینترنتی

یک مثال عملی

دیدگاه خود را ثبت کنید

دیدگاهتان را بنویسید لغو پاسخ

تلفن های تماس:

ساعات کاری

پیوند ها :

محصولات :