تعریف رگرسیون خطی (Linear Regression) قسمت 4

مفهوم رگرسیون

در آمار، رگرسیون خطی یک روریکرد مدل خطی بین متغیر «پاسخ» (Response) با یک یا چند متغیر «توصیفی» (Explanatory) است. اغلب برای کشف مدل رابطه‌ی خطی بین متغیرها از رگرسیون (Regression) استفاده می‌شود. در این حالت فرض بر این است که یک یا چند متغیر توصیفی که مقدار آن‌ها مستقل از بقیه متغیرها یا تحت کنترل محقق است، می‌تواند در پیش‌بینی متغیر پاسخ که مقدارش وابسته به متغیرهای توصیفی و تحت کنترل محقق نیست، موثر باشد. هدف از انجام تحلیل رگرسیون شناسایی مدل خطی این رابطه‌ است.

در ادامه از  متغیر وابسته به جای متغیر پاسخ و متغیر مستقل به جای متغیر توصیفی استفاده می‌کنیم.

از آنجایی که ممکن است علاوه بر متغیرهای مستقل، عوامل زیاد و ناشناخته‌ دیگری نیز در تعیین مقدار متغیر وابسته نقش داشته باشند، مدل رگرسیونی را با مناسب‌ترین تعداد متغیر مستقل در نظر گرفته و میزان خطا را به عنوان نماینده عوامل تصادفی دیگری که قابل شناسایی نبودند در نظر می‌گیریم که انتظار است کمتر در تغییرات متغیر وابسته نقش داشته باشند.

تاریخچه رگرسیون

واژه رگرسیون برای اولین بار در مقاله‌ معروف فرانسیس گالتون دیده شد که در مورد قد فرزندان و والدینشان بود. این واژه به معنی بازگشت است. او در مقاله خود در سال 1۸۷۷ اشاره می‌کند که قد فرزندان قد بلند به میانگین قد جامعه میل می‌کند. او این رابطه را «بازگشت» (Regress) نامید.

هر چند واژه رگرسیون در شاخه علوم زیستی معرفی شد ولی آنچه امروزه به نام رگرسیون می‌شناسیم،‌ روشی است که توسط «گاوس» (Gauss) در سال 1۸۰۹ معرفی شد تا به کمک آن پارامترهای مجهول رابطه بین مدار سیاره‌های منظومه شمسی را برآورد کند.

بعدها روش گاوس توسط پیرسون (Pearson) توسعه یافت و با مفاهیم آماری آمیخته شد. همچنین پیرسون توزیع توام متغیر وابسته و مستقل را توزیع گاوسی در نظر گرفت. بعدها «فیشر» (R. A. Fisher) توزیع متغیر وابسته به شرط متغیر مستقل را توزیع گاوسی محسوب کرد.

مدل رگرسیون خطی ساده

اگر برای شناسایی و پیش‌بینی متغیر وابسته فقط از یک متغیر مستقل استفاده شود، مدل را «رگرسیون خطی ساده» (Simple Linear Regression) می‌گویند. فرم مدل رگرسیون خطی ساده به صورت زیر است:

$$Y={\beta }_0+{\beta }_{1}X+ϵ$$

همانطور که دیده می‌شود این رابطه، معادله یک خط است که جمله خطا یا همان $$ϵ$$‌ به آن اضافه شده. پارامترهای این مدل خطی عرض از مبدا ($${\beta }_0$$) و شیب خط ($${\beta }_1$$) است. شیب خط در حالت رگرسیون خطی ساده، نشان می‌دهد که میزان حساسیت متغیر وابسته به متغیر مستقل چقدر است. به این معنی که با افزایش یک واحد به مقدار متغیر مستقل چه میزان متغیر وابسته تغییر خواهد کرد. عرض از مبدا نیز بیانگر مقداری از متغیر وابسته است که به ازاء مقدار متغیر مستقل برابر با صفر محاسبه می‌شود. به شکل دیگر می‌توان مقدار ثابت یا عرض از مبدا را مقدار متوسط متغیر وابسته به ازاء حذف متغیر مستقل در نظر گرفت.

برای مثال فرض کنید کارخانه‌ای می‌خواهد میزان هزینه‌هایش را براساس ساعت کار برآورد کند. شیب خط حاصل از برآورد نشان می‌دهد به ازای یک ساعت افزایش ساعت کاری چه میزان بر هزینه‌هایش افزوده خواهد شد. از طرفی عرض از مبدا خط رگرسیون نیز هزینه ثابت کارخانه حتی زمانی که ساعت کاری نیست نشان می‌دهد. این هزینه را می‌توان هزینه‌های ثابت مانند دستمزد نگهبانان و هزینه روشنایی فضای کارخانه فرض کرد.

گاهی مدل رگرسیونی را بدون عرض از مبدا در نظر می‌گیرند و  $${\beta }_0=0$$ محسوب می‌کنند. این کار به این معنی است که با صفر شدن مقدار متغیر مستقل، مقدار متغیر وابسته نیز باید صفر در نظر گرفته شود. زمانی که محقق مطمئن باشد که که خط رگرسیون باید از مبدا مختصات عبور کند، این گونه مدل در نظر گرفته می‌شود. فرم مدل رگرسیونی در این حالت به صورت زیر است:

$$Y={\beta }_{1}X+ϵ$$

از آنجایی که پیش‌بینی رابطه بین متغیر وابسته و مستقل به شکل دقیق نیست، جمله خطا را یک «متغیر تصادفی» (Random Variable) با میانگین صفر در نظر می‌گیرند تا این رابطه دارای اریبی نباشد.

باید توجه داشت که منظور از رابطه خطی در مدل رگرسیون، وجود رابطه خطی بین ضرایب است نه بین متغیرهای مستقل. برای مثال این مدل $$y={\beta }_0+{\beta }_1{x}^2+ϵ$$ را نیز می‌توان مدل خطی در نظر گرفت در حالیکه مدل $$y={\beta }_0{x}^{{\beta }_1}+ϵ$$ دیگر خطی نیست و به مدل نمایی شهرت دارد.

همچنین در فرضیات این مدل، خطا یک جمله تصادفی است و تغییرات آن مستقل از متغیر X‌ است. به این ترتیب مقدار خطا وابسته به مقدار متغیر مستقل نیست.

در رگرسیون خطی سعی می‌شود، به کمک معادله خطی که توسط روش رگرسیون معرفی می‌شود، برآورد مقدار متغیر وابسته به ازای مقدارهای مختلف متغیر مستقل توسط خط رگرسیون بدست آید. به منظور برآورد پارامترهای مناسب برای مدل، کوشش می‌شود براساس داده‌های موجود، مدلی انتخاب می‌شود که کمترین خطا را داشته باشد.

روش‌های مختلفی برای تعریف خطا و حداقل کردن آن وجود دارد. معیاری که در مدل رگرسیون خطی ساده به کار می‌رود، کمینه کردن مجموع مربعات خطا است. از آنجایی که میانگین مقدارهای خطا صفر در نظر گرفته شده است، می‌دانیم زمانی مجموع مربعات خطا، حداقل ممکن را خواهد داشت که توزیع داده‌ها نرمال باشند. در نتیجه، نرمال بودن داده‌های متغییر وابسته یا باقی‌مانده‌ها یکی از فرضیات مهم برای مدل رگرسیونی خطی ساده است.

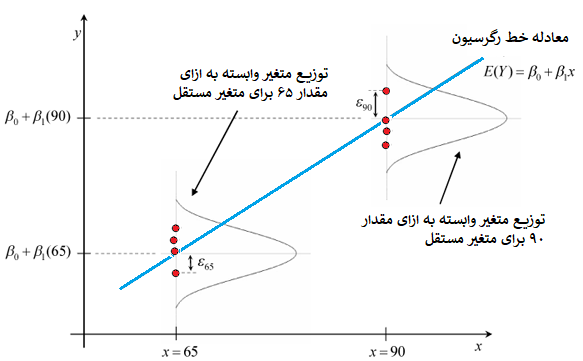
شکل زیر به منظور توضیح نرمال بودن مقدار خطا ترسیم شده است. در هر مقدار از متغیر مستقل ممکن است بیش از یک مقدار برای متغیر وابسته مشاهده شود. مقدار پیش‌بینی شده برای هر یک از این مقدارها ثابت است که توسط معادله خط رگرسیون برآورد می‌شود.

برای مثال تعدادی مقدار برای متغیر وابسته براساس مقدار x=65 وجود دارد که شکل توزیع فراوانی آن‌ها به صورت نرمال با میانگین $${\beta }_0+{\beta }_1\times 65$$ است. همچنین برای نقطه ۹۰ نیز مقدار پیش‌بینی یا برآورد برای متغیر وابسته به صورت $${\beta }_0+{\beta }_1\times 90$$ خواهد بود. در هر دو حالت واریانس خطا یا واریانس مقدارهای پیش‌بینی‌شده (پهنای منحنی زنگی شکل)  ثابت است.

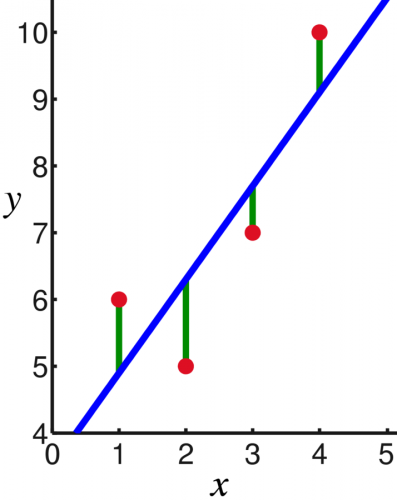
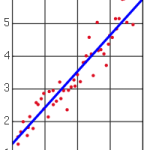
در تصویر زیر چهار نقطه از مشاهدات (x,y) به همراه خط رگرسیون دیده می‌شوند که در آن خط رگرسیون با رنگ آبی، نقطه‌های مربوط به مشاهدات با رنگ قرمز و فاصله هر نقطه از خط رگرسیون (خطای برآورد) با رنگ سبز نشان داده شده است.

برای برآورد کردن پارامترهای مدل رگرسیونی باید معادله خطی یافت شود که از بین همه خطوط دیگر دارای کمترین مجموع توان دوم خطا باشد. یعنی $$\sum {ϵ}^2$$ برای آن از بقیه خطوط کمتر باشد.

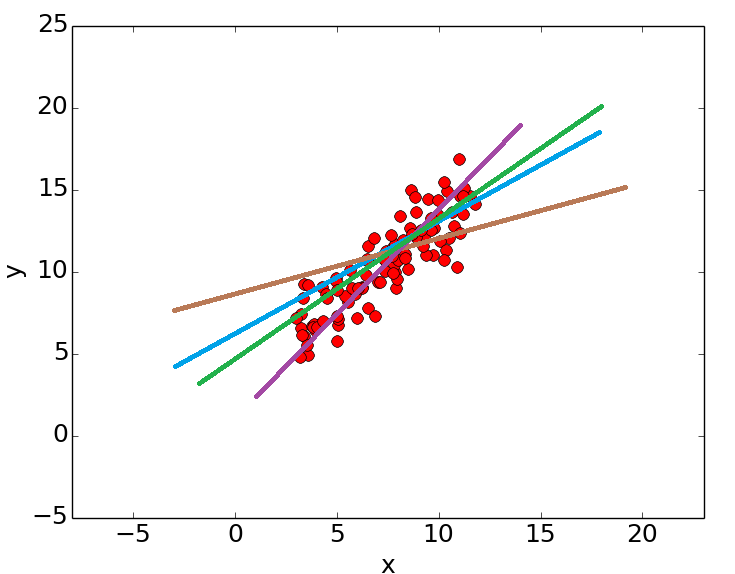
به نظر شما در تصویر بالا،‌ کدام خط دارای مجموع مربعات خطای کمتری است؟ امکان تشخیص بهترین خط بدون استفاده از ابزارهای محاسباتی امکان‌پذیر نیست.

تعریف رگرسیون خطی (Linear Regression) قسمت 1
تعریف رگرسیون خطی (Linear Regression) قسمت 2
تعریف رگرسیون خطی (Linear Regression) قسمت 3
تعریف رگرسیون خطی (Linear Regression) قسمت 4
تعریف رگرسیون خطی (Linear Regression) قسمت 5
تعریف رگرسیون خطی (Linear Regression) قسمت 6
تعریف رگرسیون خطی (Linear Regression) قسمت 7