بایگانی‌های Linear Regression

بایگانی برچسب برای: Linear Regression

تعریف رگرسیون خطی (Linear Regression) قسمت 6

آزمون مربوط به مدل و پارامترهای آن

بعد از انجام مراحل رگرسیون، با استفاده از جدول «تحلیل واریانس» (Analysis of Variance) می‌توان صحت مدل ایجاد شده و کارایی آن را سنجید. اساس کار در تحلیل واریانس، تجزیه واریانس متغیر وابسته به دو بخش است، بخشی از تغییرات یا پراکندگی که توسط مدل رگرسیونی قابل نمایش است و بخشی که توسط جمله خطا تعیین می‌شود. پس می‌توان رابطه زیر را بر این اساس نوشت.

SST= SSR+SSE

که هر کدام به صورت زیر تعریف شده‌اند:

$S S T = \sum (y_{i} - ¯ ¯ ¯ y)^{2}$

مقدار SST را می‌توان مجموع مربعات تفاضل مشاهدات متغیر وابسته با میانگینشان در نظر گرفت که در حقیقت صورت کسر واریانس متغیر وابسته است. این کمیت می‌تواند به دو بخش زیر تفکیک شود.

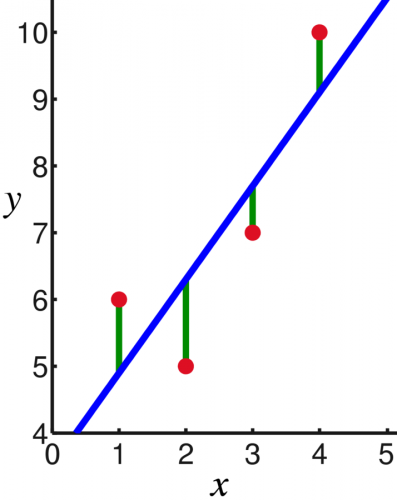
$S S E = \sum (y_{i} - {ˆ y}_{i})^{2}$

شایان ذکر است به مقدار SSE مجموع مربعات خطا نیز گفته می‌شود که در مدل رگرسیون با توجه به کمینه کردن آن پارامترهای مدل بدست آمد. همچنین بخش بعدی با SSR‌ نشان داده می‌شود:

$S S R = \sum ({ˆ y}_{i} - ¯ ¯ ¯ y)^{2}$

که می‌تواند به عنوان مجموع مربعات تفاضل مقدارهای پیش‌بینی‌شده از میانگینشان نام‌گذاری شود.

در صورتی که مدل رگرسیون مناسب باشد،‌ انتظار داریم سهم SSR از SST زیاد باشد، بطوری که بیشتر تغییرات متغیر وابسته توسط مدل رگرسیون توصیف شود. برای محاسبه واریانس از روی هر یک از مجموع مربعات کافی است حاصل را بر تعداد اعضایشان تقسیم کنیم. به این ترتیب مقدارهای جدیدی به نام «میانگین مربعات خطا» (MSE)،‌ «میانگین مربعات رگرسیون» (MSR) بوجود می‌آیند. به جدول زیر که به جدول تحلیل واریانس معروف است، توجه کنید.

منشاء تغییرات	درجه آزادی	مجموع مربعات	میانگین مربعات	آماره F
رگرسیون	k-1	SSR	$M S R = \frac{S S R}{k - 1}$	$F = \frac{M S R}{M S E}$
خطا	n-k	SSE	$M S E = \frac{S S E}{n - k}$
کل	n-1	SST

درجه آزادی برای رگرسیون که با k-1 نشان داده شده است، یکی کمتر از تعداد پارامترهای مدل (k) است که در رگرسیون خطی ساده برابر با 1-2=1 خواهد بود زیرا پارامترهای مدل در این حالت $β_{0}$ و $β_{1}$ هستند. تعداد مشاهدات نیز با n نشان داده شده است.

اگر محاسبات مربوط به جدول تحلیل واریانس را برای مثال ذکر شده، انجام دهیم نتیجه مطابق جدول زیر خواهد بود.

منشاء تغییرات	درجه آزادی	مجموع مربعات	میانگین مربعات	آماره F
رگرسیون	1	520338.1755	520338.1755	$F = \frac{M S R}{M S E} = \frac{520338.1755}{239.91} = 2168.89$
خطا	48	11515.7187	239.91
کل	49	531853.8942

از آنجایی که نسبت میانگین مربعات دارای توزیع آماری F است با مراجعه به جدول این توزیع متوجه می‌شویم که مقدار محاسبه شده برای F بزرگتر از مقدار جدول توزیع F با $k - 1$ ‌ و $n - k$ درجه آزادی است، پس مدل رگرسیون توانسته است بیشتر تغییرات متغیر وابسته را در خود جای دهد در نتیجه مدل مناسبی توسط روش رگرسیونی ارائه شده.

گاهی از «ضریب تعیین» (Coefficient of Determination) برای نمایش درصدی از تغییرات که توسط مدل رگرسیونی بیان شده، استفاده می‌شود. ضریب تعیین را با علامت $R^{2}$ نشان می‌دهند. هر چه ضریب تعیین بزرگتر باشد، نشان‌دهنده موفقیت مدل در پیش‌بینی متغیر وابسته است. در رگرسیون خطی ساده مربع ضریب همبستگی خطی همان ضریب تعیین خواهد بود.

در مثال قبل ضریب تعیین برای مدل رگرسیونی برابر با 0.9783‌ است. بنابراین به نظر می‌رسد که مدل رگرسیونی در پیش‌بینی ارزش خانه برحسب متراژ موفق عمل کرده.

نکاتی در مورد رگرسیون خطی ساده

قبل از اتمام کار با مدل رگرسیون نکاتی باید در نظر گرفته شوند. با توجه به تعریف فیشر برای رگرسیون، جمله‌ خطا باید یک متغیر تصادفی با توزیع نرمال باشد. از آنجایی که در انجام محاسبات این فرضیه چک نشده است، باید بعد از محاسبات مربوط به مدل رگرسیون خطی، مقدارهای خطا محاسبه شده و تصادفی بودن و وجود توزیع نرمال برای آن‌ها چک شود.

تصادفی بودن باقی‌مانده‌ها

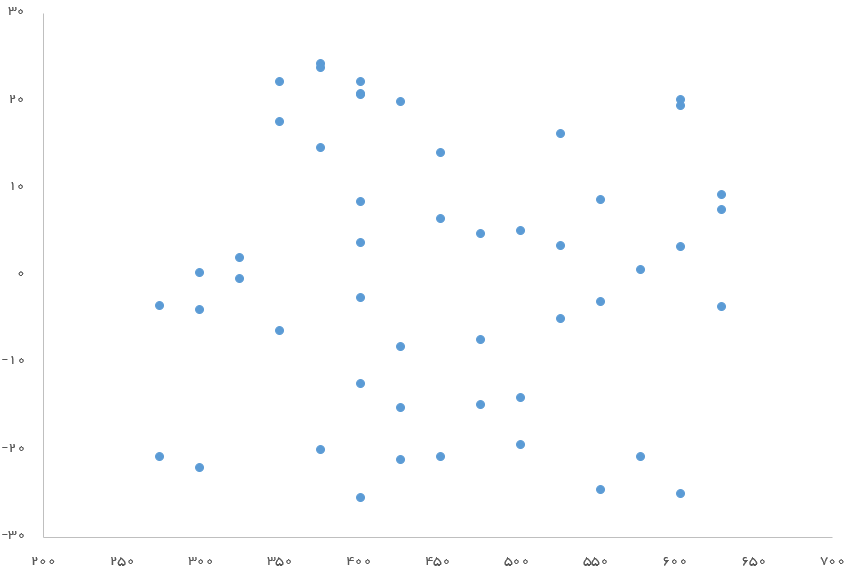
یک راه ساده، برای چک کردن تصادفی بودن مقدارهای خطا می‌تواند رسم آن‌ها و مقدار پیش‌بینی شده $ˆ y$ روی یک نمودار باشد، بطوری که مقدارهای پیش‌بینی در محور افقی و مقدارهای خطا در محور عمودی ظاهر شوند. اگر در این نمودار، الگوی خاصی مشاهده نشود می‌توان رای به تصادفی بودن باقی‌مانده داد. منظور از الگوی غیرتصادفی، افزایش یا کاهش مقدار خطا با افزایش یا کاهش مقدارهای پیش‌بینی‌ شده است.

در تصویر زیر این نمودار برای مثال قبلی ترسیم شده است. محور افقی در این نمودار مقدار قیمت خانه و محور عمودی نیز باقی‌مانده‌ها است. همانطور که دیده می‌شود، الگوی خاصی وجود ندارد.

randomness — نمودار نقطه‌ای برای نمایش رابطه بین مقدارهای پیش‌بینی شده و باقی‌مانده‌ها

تعریف رگرسیون خطی (Linear Regression) قسمت 1
تعریف رگرسیون خطی (Linear Regression) قسمت 2
تعریف رگرسیون خطی (Linear Regression) قسمت 3
تعریف رگرسیون خطی (Linear Regression) قسمت 4
تعریف رگرسیون خطی (Linear Regression) قسمت 5
تعریف رگرسیون خطی (Linear Regression) قسمت 6
تعریف رگرسیون خطی (Linear Regression) قسمت 7

آگوست 25, 2019/0 دیدگاه /توسط hgadmin

تعریف رگرسیون خطی (Linear Regression) قسمت 5

آموزش عمومی پردازش تصویر و بینایی ماشین

برآورد پارامترهای رگرسیون خطی ساده

به منظور برآورد پارامترهای رگرسیون خطی ساده، کافی است تابع مجموع مربعات خطا را کمینه کرد. برای این کار مراحل زیر باید طی شوند:

محاسبه مجموع توان دوم خطا

$\sum (y_{i} - ({ˆ β}_{0} + {ˆ β}_{1} x_{i}))^{2}$

مشتق مجموع مربعات خطا برحسب پارامتر ${ˆ β}_{0}$

$\sum (- y_{i} + {ˆ β}_{0} + {ˆ β}_{1} x_{i})$

برابر قرار دادن مشتق با صفر به منظور پیدا کردن نقاط کمینه

$\sum (- y_{i} + {ˆ β}_{0} + {ˆ β}_{1} x_{i}) = 0$

پیدا کردن ریشه برای معادله حاصل برحسب ${ˆ β}_{0}$

${ˆ β}_{0} = ¯ y - {ˆ β}_{1} ¯ x$

مشتق مجموع مربعات خطا بر حسب پارامتر ${ˆ β}_{1}$

$\sum (- 2 x_{i} y_{i} + 2 {ˆ β}_{0} x_{i} + 2 {ˆ β}_{1} x_{i}^{2})$

جایگذاری ${ˆ β}_{0}$ و پیدا کردن ریشه برای معادله حاصل برحسب ${ˆ β}_{1}$

$- \sum (x_{i} y_{i} + (¯ y - {ˆ β}_{1} ¯ x) \sum x_{i} + {ˆ β}_{1} \sum x_{i}^{2}) = 0$

$_{1} = \frac{\sum (x_{i} - ¯ x) (y_{i} - ¯ y)}{\sum (x_{i} - ¯ x)^{2}}$

به این ترتیب برآورد پارامترهای مدل خطی به صورت زیر خواهند بود.

$_{1} = \frac{\sum (x_{i} - ¯ x) (y_{i} - ¯ y)}{\sum (x_{i} - ¯ x)^{2}}$

$_{0} = ¯ y -_{1} ¯ x$

که در آن $¯ x$ و $¯ y$ میانگین $x$ و $y$ هستند.

برای راحتی محاسبات، می‌توان برآورد $β_{1}$ را به فرم دیگری نیز نوشت:

$_{1} = \frac{n (¯ ¯¯¯¯ ¯ x y - ¯ x ¯ y))}{(n - 1) σ_{x}^{2}}$

که منظور از $¯ ¯¯¯¯ ¯ x y$ میانگین حاصلضرب x و y بوده و $σ_{x}^{2}$ نیز بیانگر واریانس مقدارهای x است.

اگر $ˆ y$ مقدار برآورد برای متغیر وابسته باشد، می‌توانیم آن را میانگین مشاهدات برای متغیر وابسته به ازای مقدار ثابت متغیر مستقل در نظر گرفت. پس با فرض اینکه میانگین جمله خطا نیز صفر است، خواهیم داشت:

$ˆ y = E (Y | X = x) =_{0} +_{1} x$

که در آن $E (Y | X = x)$ نشان‌دهنده امید ریاضی (متوسط) شرطی است و همچنین $_{0}$ و ${ˆ β}_{1}$ برآوردهای مربوط به هر یک از پارامترها هستند.

نکته: به راحتی دیده می‌شود که میانگین مربوط به متغیر مستقل و وابسته روی خط رگرسیون قرار دارند. یعنی این نقطه در معادله خط رگرسیون صدق می‌کند. زیرا با توجه به محاسبه $β_{0}$ داریم:

$_{0} = ¯ y -_{1} ¯ x \to ¯ ¯¯ ¯ Y = {ˆ β}_{0} + {ˆ β}_{1} ¯ ¯¯¯ ¯ X$

مثال

اطلاعات مربوط به ۵۰ خانه شامل قیمت (به میلیون ریال) و متراژ (متر مربع) در شهر تهران جمع‌آوری شده است. این اطلاعات را می‌توانید با قالب اکسل از اینجا دریافت کنید.

با توجه به ضریب همبستگی بین این دو متغیر که برابر با 0.9891 است،‌ مشخص است که رابطه خطی شدیدی بینشان برقرار است. اگر فرض کنیم قیمت خانه متغیری وابسته به متراژ است، محاسبات اولیه برای برآورد پارامترهای مدل رگرسیونی در جدول زیر قرار گرفته.

$¯ ¯¯¯ ¯ X$	$¯ ¯¯ ¯ Y$	$¯ ¯¯¯¯¯¯¯ ¯ X Y$	$σ_{X}^{2}$
84.9	451.136	40350.6	411.724

بر این اساس برآورد پارامترهای مدل خطی به صورت ${ˆ β}_{0} = 19.965$ و ${ˆ β}_{1} = 5.078$ خواهد بود. در نتیجه می‌توان معادله مربوط برآورد مقدار متغیر وابسته را به صورت زیر نوشت:

$_{i} = 19.965 + 5.078 x_{i}$

پس اگر لازم باشد که ارزش خانه‌ای با متراژ 61 متر محاسبه شود، کافی است در معادله بالا برای $x_{i}$ ‌ مقدار 61 را جایگزین کرده،‌ مقدار ${ˆ y}_{i}$ را بدست آوریم که برابر با 329.758 میلیون ریال است. در تصویر زیر نمودار مربوط به داده‌ها و خط رگرسیون دیده می‌شود.

$_{i} = 19.965 + 5.078 (61) = 329.758$

آگوست 25, 2019/0 دیدگاه /توسط hgadmin

تعریف رگرسیون خطی (Linear Regression) قسمت 4

آموزش عمومی پردازش تصویر و بینایی ماشین

مفهوم رگرسیون

در آمار، رگرسیون خطی یک روریکرد مدل خطی بین متغیر «پاسخ» (Response) با یک یا چند متغیر «توصیفی» (Explanatory) است. اغلب برای کشف مدل رابطه‌ی خطی بین متغیرها از رگرسیون (Regression) استفاده می‌شود. در این حالت فرض بر این است که یک یا چند متغیر توصیفی که مقدار آن‌ها مستقل از بقیه متغیرها یا تحت کنترل محقق است، می‌تواند در پیش‌بینی متغیر پاسخ که مقدارش وابسته به متغیرهای توصیفی و تحت کنترل محقق نیست، موثر باشد. هدف از انجام تحلیل رگرسیون شناسایی مدل خطی این رابطه‌ است.

در ادامه از متغیر وابسته به جای متغیر پاسخ و متغیر مستقل به جای متغیر توصیفی استفاده می‌کنیم.

از آنجایی که ممکن است علاوه بر متغیرهای مستقل، عوامل زیاد و ناشناخته‌ دیگری نیز در تعیین مقدار متغیر وابسته نقش داشته باشند، مدل رگرسیونی را با مناسب‌ترین تعداد متغیر مستقل در نظر گرفته و میزان خطا را به عنوان نماینده عوامل تصادفی دیگری که قابل شناسایی نبودند در نظر می‌گیریم که انتظار است کمتر در تغییرات متغیر وابسته نقش داشته باشند.

تاریخچه رگرسیون

واژه رگرسیون برای اولین بار در مقاله‌ معروف فرانسیس گالتون دیده شد که در مورد قد فرزندان و والدینشان بود. این واژه به معنی بازگشت است. او در مقاله خود در سال 1۸۷۷ اشاره می‌کند که قد فرزندان قد بلند به میانگین قد جامعه میل می‌کند. او این رابطه را «بازگشت» (Regress) نامید.

هر چند واژه رگرسیون در شاخه علوم زیستی معرفی شد ولی آنچه امروزه به نام رگرسیون می‌شناسیم،‌ روشی است که توسط «گاوس» (Gauss) در سال 1۸۰۹ معرفی شد تا به کمک آن پارامترهای مجهول رابطه بین مدار سیاره‌های منظومه شمسی را برآورد کند.

بعدها روش گاوس توسط پیرسون (Pearson) توسعه یافت و با مفاهیم آماری آمیخته شد. همچنین پیرسون توزیع توام متغیر وابسته و مستقل را توزیع گاوسی در نظر گرفت. بعدها «فیشر» (R. A. Fisher) توزیع متغیر وابسته به شرط متغیر مستقل را توزیع گاوسی محسوب کرد.

مدل رگرسیون خطی ساده

اگر برای شناسایی و پیش‌بینی متغیر وابسته فقط از یک متغیر مستقل استفاده شود، مدل را «رگرسیون خطی ساده» (Simple Linear Regression) می‌گویند. فرم مدل رگرسیون خطی ساده به صورت زیر است:

$Y = β_{0} + β_{1} X + ϵ$

همانطور که دیده می‌شود این رابطه، معادله یک خط است که جمله خطا یا همان $ϵ$ ‌ به آن اضافه شده. پارامترهای این مدل خطی عرض از مبدا ( $β_{0}$ ) و شیب خط ( $β_{1}$ ) است. شیب خط در حالت رگرسیون خطی ساده، نشان می‌دهد که میزان حساسیت متغیر وابسته به متغیر مستقل چقدر است. به این معنی که با افزایش یک واحد به مقدار متغیر مستقل چه میزان متغیر وابسته تغییر خواهد کرد. عرض از مبدا نیز بیانگر مقداری از متغیر وابسته است که به ازاء مقدار متغیر مستقل برابر با صفر محاسبه می‌شود. به شکل دیگر می‌توان مقدار ثابت یا عرض از مبدا را مقدار متوسط متغیر وابسته به ازاء حذف متغیر مستقل در نظر گرفت.

برای مثال فرض کنید کارخانه‌ای می‌خواهد میزان هزینه‌هایش را براساس ساعت کار برآورد کند. شیب خط حاصل از برآورد نشان می‌دهد به ازای یک ساعت افزایش ساعت کاری چه میزان بر هزینه‌هایش افزوده خواهد شد. از طرفی عرض از مبدا خط رگرسیون نیز هزینه ثابت کارخانه حتی زمانی که ساعت کاری نیست نشان می‌دهد. این هزینه را می‌توان هزینه‌های ثابت مانند دستمزد نگهبانان و هزینه روشنایی فضای کارخانه فرض کرد.

گاهی مدل رگرسیونی را بدون عرض از مبدا در نظر می‌گیرند و $β_{0} = 0$ محسوب می‌کنند. این کار به این معنی است که با صفر شدن مقدار متغیر مستقل، مقدار متغیر وابسته نیز باید صفر در نظر گرفته شود. زمانی که محقق مطمئن باشد که که خط رگرسیون باید از مبدا مختصات عبور کند، این گونه مدل در نظر گرفته می‌شود. فرم مدل رگرسیونی در این حالت به صورت زیر است:

$Y = β_{1} X + ϵ$

از آنجایی که پیش‌بینی رابطه بین متغیر وابسته و مستقل به شکل دقیق نیست، جمله خطا را یک «متغیر تصادفی» (Random Variable) با میانگین صفر در نظر می‌گیرند تا این رابطه دارای اریبی نباشد.

باید توجه داشت که منظور از رابطه خطی در مدل رگرسیون، وجود رابطه خطی بین ضرایب است نه بین متغیرهای مستقل. برای مثال این مدل $y = β_{0} + β_{1} x^{2} + ϵ$ را نیز می‌توان مدل خطی در نظر گرفت در حالیکه مدل $y = β_{0} x^{β_{1}} + ϵ$ دیگر خطی نیست و به مدل نمایی شهرت دارد.

همچنین در فرضیات این مدل، خطا یک جمله تصادفی است و تغییرات آن مستقل از متغیر X‌ است. به این ترتیب مقدار خطا وابسته به مقدار متغیر مستقل نیست.

در رگرسیون خطی سعی می‌شود، به کمک معادله خطی که توسط روش رگرسیون معرفی می‌شود، برآورد مقدار متغیر وابسته به ازای مقدارهای مختلف متغیر مستقل توسط خط رگرسیون بدست آید. به منظور برآورد پارامترهای مناسب برای مدل، کوشش می‌شود براساس داده‌های موجود، مدلی انتخاب می‌شود که کمترین خطا را داشته باشد.

روش‌های مختلفی برای تعریف خطا و حداقل کردن آن وجود دارد. معیاری که در مدل رگرسیون خطی ساده به کار می‌رود، کمینه کردن مجموع مربعات خطا است. از آنجایی که میانگین مقدارهای خطا صفر در نظر گرفته شده است، می‌دانیم زمانی مجموع مربعات خطا، حداقل ممکن را خواهد داشت که توزیع داده‌ها نرمال باشند. در نتیجه، نرمال بودن داده‌های متغییر وابسته یا باقی‌مانده‌ها یکی از فرضیات مهم برای مدل رگرسیونی خطی ساده است.

شکل زیر به منظور توضیح نرمال بودن مقدار خطا ترسیم شده است. در هر مقدار از متغیر مستقل ممکن است بیش از یک مقدار برای متغیر وابسته مشاهده شود. مقدار پیش‌بینی شده برای هر یک از این مقدارها ثابت است که توسط معادله خط رگرسیون برآورد می‌شود.

برای مثال تعدادی مقدار برای متغیر وابسته براساس مقدار x=65 وجود دارد که شکل توزیع فراوانی آن‌ها به صورت نرمال با میانگین $β_{0} + β_{1} \times 65$ است. همچنین برای نقطه ۹۰ نیز مقدار پیش‌بینی یا برآورد برای متغیر وابسته به صورت $β_{0} + β_{1} \times 90$ خواهد بود. در هر دو حالت واریانس خطا یا واریانس مقدارهای پیش‌بینی‌شده (پهنای منحنی زنگی شکل) ثابت است.

در تصویر زیر چهار نقطه از مشاهدات (x,y) به همراه خط رگرسیون دیده می‌شوند که در آن خط رگرسیون با رنگ آبی، نقطه‌های مربوط به مشاهدات با رنگ قرمز و فاصله هر نقطه از خط رگرسیون (خطای برآورد) با رنگ سبز نشان داده شده است.

Linear_least_squares — نمودار نقطه‌ای متغیر مستقل و وابسته،‌ میزان خطا و خط رگرسیون

برای برآورد کردن پارامترهای مدل رگرسیونی باید معادله خطی یافت شود که از بین همه خطوط دیگر دارای کمترین مجموع توان دوم خطا باشد. یعنی $\sum ϵ^{2}$ برای آن از بقیه خطوط کمتر باشد.

points_for_linear_regression — خطوط مناسب برای بیان رابطه بین متغیر مستقل و وابسته

به نظر شما در تصویر بالا،‌ کدام خط دارای مجموع مربعات خطای کمتری است؟ امکان تشخیص بهترین خط بدون استفاده از ابزارهای محاسباتی امکان‌پذیر نیست.

آگوست 25, 2019/0 دیدگاه /توسط hgadmin

تعریف رگرسیون خطی (Linear Regression) قسمت 3

آموزش عمومی پردازش تصویر و بینایی ماشین

تنظیم مدل (Regularization)

پیچیدگی مدلهای پارامتری با تعداد پارامترهای مدل و مقادیر آن‌ها سنجیده می‌شود. هرچه این پیچیدگی بیشتر باشد خطر بیش‌برازش (Overfitting) برای مدل بیشتر است پدیده بیش‌برازش زمانی رخ می‌دهد که مدل بجای یادگیری الگوهای داده، داده را را حفظ می‌کند و در عمل یادگیری به خوبی انجام نمی‌شود. برای جلوگیری از بیش‌برازش در مدلهای خطی مانند رگرسیون خطی یارگرسیون لجستیک جریمه‌ای به تابع هزینه اضافه می‌شود تا از افزایش زیاد پارامترها جلوگیری شود. به این کار تنظیم مدل یا Regularization گفته می‌شود. دو راه متداول تنظیم مدلهای خطی روشهای $L_{1}$ و $L_{2}$ هستند. در روش $L_{1}$ ضریبی از نُرمِ $L_{1}$ به تابع هزینه اضافه می‌شود و در روش $L_{2}$ ضریبی از نُرمِ $L_{2}$ که همان نُرمِ اقلیدسی است به تابع هزینه اضافه می‌شود.

در تنظیم مدل به روش $L_{1}$ تابع هزینه را به این شکل تغییر می‌دهیم:

$L_{r}(D,{\vec {\beta }})=L(D,{\vec {\beta }})+\lambda ||{\vec {\beta }}||_{1}=\sum _{i=1}^{n}({\vec {\beta }}\,.\,{\vec {x_{i}}}-y_{i})^{2}+\lambda \sum _{k=0}^{m}|\beta _{k}|$

این روش تنظیم مدل که به روش لاسو (Lasso) نیز شهرت دارد باعث می‌شود که بسیاری از پارامترهای مدل نهائی صفر شوند و مدل به اصلاح خلوت (Sparse) شود.

در تنظیم مدل به روش $L_{2}$ تابع هزینه را به این شکل تغییر می‌دهیم:

$L_{r}(D,{\vec {\beta }})=L(D,{\vec {\beta }})+\lambda ||{\vec {\beta }}||_{2}^{2}=\sum _{i=1}^{n}({\vec {\beta }}\,.\,{\vec {x_{i}}}-y_{i})^{2}+\lambda \sum _{k=0}^{m}\beta _{k}^{2}$

در روش تنظیم از طریق $L_{2}$ سعی می‌شود طول اقلیدسی بردار ${\vec {\beta }}$ کوتاه نگه داشته شود. $\lambda$ در روش $L_{1}$ و $L_{2}$ یک عدد مثبت است که میزان تنظیم مدل را معین می‌کند. هرچقدر $\lambda$ کوچکتر باشد جریمه کمتری برا بزرگی نرم بردار پارامترها یعنی ${\vec {\beta }}$ پرداخت می‌کنیم. مقدار ایدئال $\lambda$ از طریق آزمایش بر روی داده اعتبار (Validation Data) پیدا می‌شود.

تفسیر احتمالی تنظیم مدل

اگر بجای روش درست نمایی بیشینه از روش بیشینه سازی احتمال پسین استفاده کنیم به ساختار «تنظیم مدل» یا همان regularization خواهیم رسید. اگر مجموعه داده را با $D$ نمایش بدهیم و پارامتری که به دنبال تخمین آن هستیم را با ${\vec {\beta }}$ ، احتمال پسین $Pr\left({\vec {\beta }}\,|\,D\right)$ ، طبق قانون بیز متناسب خواهد بود با حاصلضرب درست نمایی یعنی $Pr\left(D\,|\,{\vec {\beta }}\right)$ و احتمال پیشین یعنی $Pr\left({\vec {\beta }}\right)$ :

$Pr\left({\vec {\beta }}\,|\,D\right)={\frac {Pr\left(D\,|\,{\vec {\beta }}\right)\times Pr\left({\vec {\beta }}\right)}{Pr\left(D\right)}}$

ازین رو

$argmax_{\vec {\beta }}Pr\left({\vec {\beta }}\,|\,D\right)=argmax_{\vec {\beta }}{\frac {Pr\left(D\,|\,{\vec {\beta }}\right)\times Pr\left({\vec {\beta }}\right)}{Pr\left(D\right)}}=argmax_{\vec {\beta }}Pr\left(D\,|\,{\vec {\beta }}\right)\times Pr\left({\vec {\beta }}\right)$

معادله خط پیشین نشان می‌دهد که برای یافتن پارامتر بهینه فقط کافیست که احتمال پیشین را نیز در معادله دخیل کنیم. اگر احتمال پیشین را یک توزیع احتمال با میانگین صفر و کوواریانس $\tau ^{2}I$ در نظر بگیریم به معادله پایین می‌رسیم:

$argmax_{\vec {\beta }}\,\,\log Pr\left(D\,|\,{\vec {\beta }}\right)=argmax_{\vec {\beta }}\,\,\log \prod _{i=1}^{n}Pr(y_{i}|{\vec {x_{i}}}\,\,;{\vec {\beta }},\sigma )Pr\left({\vec {\beta }}\right)=argmax_{\vec {\beta }}\,\,\log \prod _{i=1}^{n}{\frac {1}{{\sqrt {2\pi }}\sigma }}exp\left(-{\frac {\left(y_{i}-{\vec {\beta }}\,.\,{\vec {x_{i}}}\right)^{2}}{2\sigma ^{2}}}\right){\frac {1}{{\sqrt {2\pi }}\tau }}exp\left(-{\frac {||{\vec {\beta }}||^{2}}{2\tau ^{2}}}\right)$

با ساده کردن این معادله به این جواب می‌رسیم، در اینجا $\lambda$ برابر است با ${\frac {\sigma ^{2}}{\tau ^{2}}}$ : $argmax_{\vec {\beta }}\,\,Pr\left(D\,|\,{\vec {\beta }}\right)=argmax_{\vec {\beta }}\left(n\log {\frac {1}{{\sqrt {2\pi }}\sigma }}-{\frac {1}{2\sigma ^{2}}}\sum _{i=1}^{n}\left(y_{i}-{\vec {\beta }}\,.\,{\vec {x_{i}}}\right)^{2}+\log {\frac {1}{{\sqrt {2\pi }}\tau }}-{\frac {1}{2\tau ^{2}}}||{\vec {\beta }}||^{2}\right)=argmin_{\vec {\beta }}\left(\sum _{i=1}^{n}\left(y_{i}-{\vec {\beta }}\,.\,{\vec {x_{i}}}\right)^{2}+\lambda ||{\vec {\beta }}||^{2}\right)$

همان‌طور که دیدیم جواب همان تنظیم مدل با نرم $L_{2}$ است.

حال اگر احتمال پیشین را از نوع توزیع لاپلاس با میانگین صفر درنظر بگیریم به تنظیم مدل با نرم $L_{1}$ خواهیم رسید.

منبع

استفاده از داده‌ها به منظور کشف رابطه بین آن‌ها اساس داده‌کاوی است. یکی از ابزار سنجش رابطه و مدل‌سازی استفاده از ابزار آماری رگرسیون است. امروزه به منظور تحلیل و کشف مدل روی «مه داده» (کلان‌داده | Big Data)، روش‌های مختلف رگرسیون توسعه یافته است. استفاده از تحلیل گرسیونی در علوم مختلف داده‌کاوی، بخصوص مبحث «آموزش ماشین» (Machine Learning)، فیزیک، شیمی و علوم زیستی کاربرد بسیاری دارد.

آگوست 24, 2019/0 دیدگاه /توسط hgadmin

تعریف رگرسیون خطی (Linear Regression) قسمت 1

آموزش عمومی پردازش تصویر و بینایی ماشین

رگرسیون خطی یا تنازل خطی یا وایازی خطی (Linear regression) یکی از روشهای تحلیل رگرسیون است. در رگرسیون خطی، متغیّر وابسته $y$ ترکیب خطی‌ای از ورودی یا متغیرهای مستقل است. البته ضرورتاً متغیر وابسته لازم نیست که نسبت به متغیرهای مستقل، خطی باشد.

رگرسیون خطی با یک متغیر مستقل

تخمین پارامترها برای مسائل تک متغیره

رگرسیون میزان اثر دو یا چند متغیر بر متغیر وابسته را می‌سنجد و همبستگی رابطه بین دو یا چند متغیر را مورد سنجش قرار می‌دهد.

مثلاً تحلیل رگرسیونی سادهٔ زیر با $N$ نقطه، متغیر مستقل $x_i$ و ضرایب $\beta _{0}$ و $\beta _{1}$ خطی است:

خط راست:

y_{i}=\beta _{0}+\beta _{1}x_{i}+\epsilon _{i},\quad i=1,\dots ,N\!

در هر دو حالت، $\epsilon _{i}$ مقدار خطاست و پانویس $i$ شمارهٔ هر مشاهده (هر جفت $x_i$ و $y_i$ ) را نشان می‌دهد. با داشتن مجموعه‌ای از این نقطه‌ها می‌توان مدل را به دست آورد:

y_{i}={\widehat {\beta }}_{0}+{\widehat {\beta }}_{1}X_{i}+e_{i}

عبارت $e_{i}$ مانده نام دارد: $e_{i}=y_{i}-{\widehat {y}}_{i}$ . روش رایج برای به‌دست‌آوردن پارامترها، روش کمترین مربعات است. در این روش پارامترها را با کمینه‌کردن تابع زیر به دست می‌آورند:

\mathrm {SSE} =\sum _{i=1}^{N}e_{i}^{2}

در مورد رگرسیون ساده، پارامترها با این روش برابر خواهند بود با:

{\widehat {\beta _{1}}}={\frac {\sum (x_{i}-{\bar {x}})(y_{i}-{\bar {y}})}{\sum (x_{i}-{\bar {x}})^{2}}}

{\hat {\beta _{0}}}={\bar {y}}-{\widehat {\beta _{1}}}{\bar {x}}

که در آن ${\bar {x}}$ و ${\bar {y}}$ میانگین $x$ و $y$ هستند.

تفاوت رگرسیون و همبستگی بر اساس هدف:

هدف مدل‌های همبستگی بررسی میزان رابطه دو یا چند متغیر است در حالیکه رگرسیون به دنبال پیش‌بینی یک یا چند متغیر براساس یک یا چند متغیر دیگر است. از آنجا که رگرسیون برپایه داده‌های گذشته انجام می‌شود به آن عنوان Regression یعنی بازگشت به گذشته داده‌اند؛ بنابراین از نظر هدف همبستگی میزان و شدت رابطه متغیرها را نشان می‌دهد اما رگرسیون معادله ای را برای پیش‌بینی متغیرها ارائه می‌کند.

تفاوت رگرسیون و همبستگی براساس روش:

آنچه در خروجی نتایج رگرسیون و همبستگی باعث ایجاد تفاوت می‌شود آن است که در همبستگی همیشه اثرات متغیرها به صورت دو به دو مورد سنجش قرار می‌گیرد اما در یک مدل رگرسیون اثرات متغیرها به صورت همزمان بررسی می‌شود. یعنی در همبستگی رابطه متغیر X با متغیر Y به وجود یا عدم وجود متغیر Z ارتباطی ندارد اما اما در رگرسیون تأثیر متغیر X بر متغیر Y به وجود یا عدم وجود متغیر Z بستگی دارد.

آگوست 24, 2019/0 دیدگاه /توسط daliri

بایگانی برچسب برای: Linear Regression

تعریف رگرسیون خطی (Linear Regression) قسمت 6

آزمون مربوط به مدل و پارامترهای آن

نکاتی در مورد رگرسیون خطی ساده

تصادفی بودن باقی‌مانده‌ها

تعریف رگرسیون خطی (Linear Regression) قسمت 5

برآورد پارامترهای رگرسیون خطی ساده

مثال

تعریف رگرسیون خطی (Linear Regression) قسمت 4

مفهوم رگرسیون

تاریخچه رگرسیون

مدل رگرسیون خطی ساده

تعریف رگرسیون خطی (Linear Regression) قسمت 3

تنظیم مدل (Regularization)

تفسیر احتمالی تنظیم مدل

تعریف رگرسیون خطی (Linear Regression) قسمت 1

تخمین پارامترها برای مسائل تک متغیره

تفاوت رگرسیون و همبستگی بر اساس هدف:

تفاوت رگرسیون و همبستگی براساس روش:

تلفن های تماس:

ساعات کاری

پیوند ها :

محصولات :