تعریف رگرسیون خطی (Linear Regression) قسمت 7
نرمال بودن باقیماندهها
به منظور سنجش نرمال بودن باقیماندهها، ترسیم بافتنگار میتواند سادهترین راه باشد. در تصویر زیر بافتنگار مربوط به باقیماندههای مثال قبل ترسیم شده است. شکل بدست آمده شبیه توزیع نرمال است و به صورت زنگی شکل درآمده.
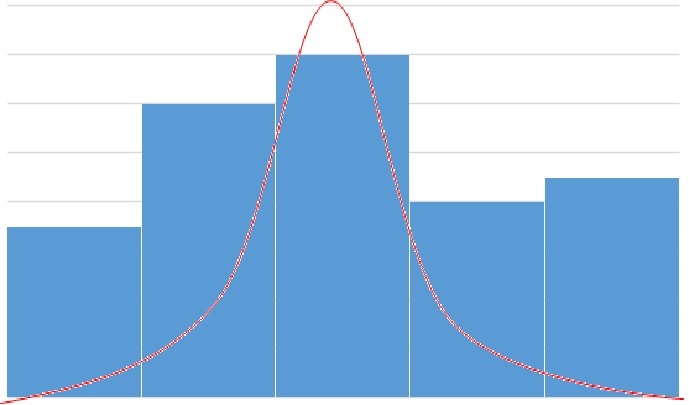
البته روش دقیقتر، ترسیم نمودار «چندک-چندک» (Q-Q Plot) برای باقیماندهها یا مشاهدات y و دادههای توزیع نرمال است. در زیر نمودار چندک-چندک برای دادههای مربوط به مثال قبل ترسیم شده است.
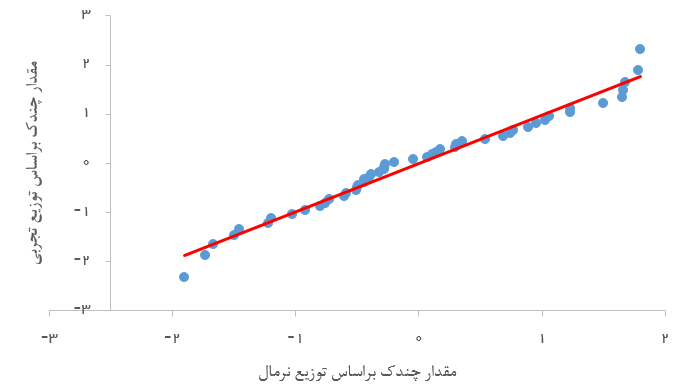
انتظار داریم در این نمودار، اگر دادههای مربوط به متغیر وابسته دارای توزیع نرمال باشند، صدکهای مربوط به آن با صدکهای تولید شده از توزیع نرمال تقریبا یکسان باشند. اگر این اتفاق بیافتد باید نقاط روی نمودار که نشاندهنده زوج صدکهای تولید شده هستند، روی یک خط راست قرار گیرند. این کار را با مقدارهای خطا نیز میتوان انجام داد زیرا متغیر وابسته با مقدارهای خطا رابطه خطی دارد. به این منظور چندکهای توزیع نرمال را با چندکهای توزیع تجربی باقیماندهها مقایسه میکنیم. انتظار داریم که نمودار، نشان دهنده یک رابطه مستقیم خطی باشد. در نتیجه میتوان فرض کرد که باقیماندهها دارای توزیع نرمال هستند.
ثابت بودن واریانس
از طرفی واریانس جمله خطا نیز طبق فرضیههای اولیه برای مدل رگرسیونی، باید ثابت و برابر با σ2 باشد. برآورد واریانس برای جملههای خطا نیز به صورت زیر است:
σ2=∑(yi−y^i)2n−2
مشخص است که مقدار yi بیانگر مقدار مشاهده شده و y^i مقدار پیشبینی برای مشاهده iام است. از آنجایی که در برآورد واریانس احتیاج به دو پارامتر مدل رگرسیونی است، دو درجه آزادی از تعداد مشاهدات کم شده است و در مخرج کسر n-2 قرار گرفته است.
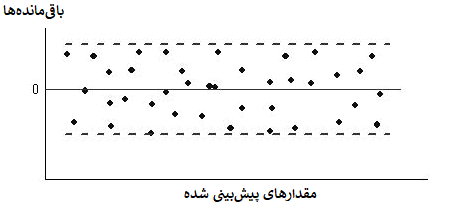
برای آنکه نشان دهیم واریانس نیز ثابت است از نمودار نقطهای استفاده میکنیم که در محور افقی مقدارهای پیشبینیشده و در محور عمودی نیز مقدار باقیماندهها قرار دارد. این نمودار نباید به صورت الگوی افزایشی یا کاهشی باشد. قبلا از این نمودار به منظور چک کردن تصادفی بودن باقیماندهها بهره بردیم.
تصویر زیر حالتی را نشان میدهد که واریانس باقیماندهها نسبت به مقدار پیشبینی حالت افزایشی دارد و ثابت نیست.
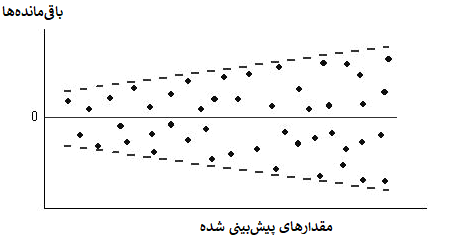
همچنین کاهشی بودن واریانس باقیماندهها نسبت به مقدار پیشبینی در تصویر زیر دیده میشود.
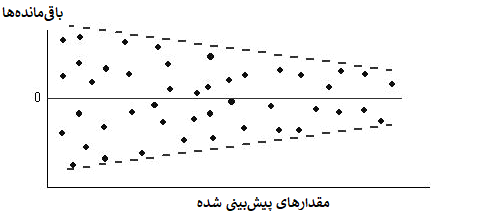
اگر در مدل رگرسیونی باقیماندهها نسبت به مقدار پیشبینی به طور تصادفی حول نقطه صفر تغییر کند، ثابت بودن واریانس قابل شناسایی است. این حالت در تصویر زیر دیده میشود.
تعریف رگرسیون خطی (Linear Regression) قسمت 1
تعریف رگرسیون خطی (Linear Regression) قسمت 2
تعریف رگرسیون خطی (Linear Regression) قسمت 3
تعریف رگرسیون خطی (Linear Regression) قسمت 4
تعریف رگرسیون خطی (Linear Regression) قسمت 5
تعریف رگرسیون خطی (Linear Regression) قسمت 6
تعریف رگرسیون خطی (Linear Regression) قسمت 7


دیدگاه خود را ثبت کنید
تمایل دارید در گفتگوها شرکت کنید؟در گفتگو ها شرکت کنید.