مدل مخفی مارکوف (Hidden Markov Model) قسمت 4
مسئله کد گشایی و الگوریتم ویتربی (Viterbi Algorithm)
در این حالت میخواهیم با داشتن دنباله مشاهدات و مدل دنباله حالات بهینه برای تولید را بهدست آوریم.
یک راه حل این است که محتملترین حالت در لحظه t را بهدست آوریم و تمام حالات را به این شکل برای دنبالهٔ ورودی بهدست آوریم. اما برخی مواقع این روش به ما یک دنبالهٔ معتبر و بامعنا از حالات را نمیدهد. به همین دلیل، باید راهی پیدا کرد که یک چنین مشکلی نداشته باشد.
در یکی از این روشها که با نام الگوریتم Viterbi شناخته میشود، دنباله حالات کامل با بیشترین مقدار نسبت شباهت پیدا میشود. در این روش برای ساده کردن محاسبات متغیر کمکی زیر را تعریف مینماییم.
که در شرایطی که حالت فعلی برابر با i باشد، بیشترین مقدار احتمال برای دنباله حالات و دنباله مشاهدات در زمان t را میدهد. به همین ترتیب میتوان روابط بازگشتی زیر را نیز بهدستآورد.
که در آن
به همین دلیل روال پیدا کردن دنباله حالات با بیشترین احتمال از محاسبهٔ مقدار و با کمک رابطهٔ فوق شروع میشود. در این روش در هر زمان یک اشاره گر به حالت برنده قبلی خواهیم داشت. در نهایت حالت را با داشتن شرط زیر بهدست میآوریم.
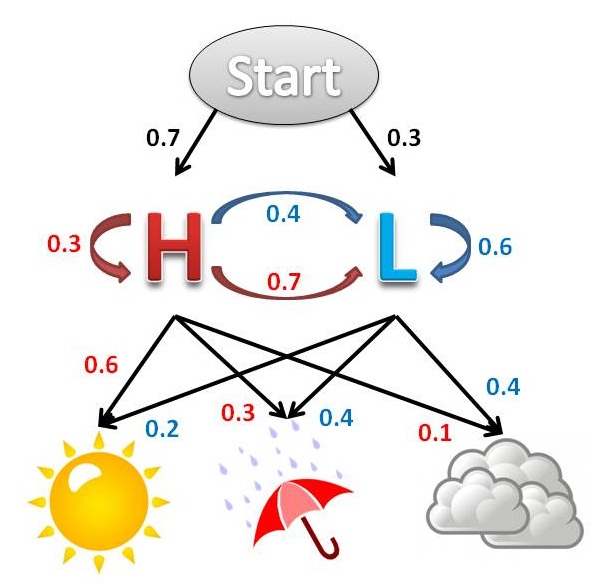
و با شروع از حالت ، دنباله حالات به شکل بازگشت به عقب و با دنبال کردن اشاره گر به حالات قبلی بهدست میآید. با استفاده از این روش میتوان مجموعه حالات مورد نظر را بهدستآورد. این الگوریتم را میتوان به صورت یک جستجو در گراف که نودهای آن برابر با حالتها مدل HMM در هر لحظه از زمان میباشند نیز تفسیر نمود
مسئله یادگیری
بهطور کلی مسئله یادگیری به این موضوع میپردازد که چگونه میتوان پارامترهای مدل HMM را تخمین زد تا مجموعه دادههای آموزشی به بهترین نحو به کمک مدل HMM برای یک کاربرد مشخص بازنمایی شوند. به همین دلیل میتوان نتیجه گرفت که میزان بهینه بودن مدل HMM برای کاربردهای مختلف، متفاوت است. به بیان دیگر میتوان از چندین معیار بهینهسازی متفاوت استفاده نمود، که از این بین یکی برای کاربرد مورد نظر مناسب تر است. دو معیار بهینهسازی مختلف برای آموزش مدل HMM وجود دارد که شامل معیار بیشترین شباهت (ML) و معیار ماکزیمم اطلاعات متقابل ((Maximum Mutual Information (MMI) میباشند. آموزش به کمک هر یک از این معیارها در ادامه توضیح داده شدهاست.
معیار بیشترین شباهت((Maximum Likelihood (ML)
در معیار ML ما سعی داریم که احتمال یک دنباله ورودی که به کلاس w تعلق دارد را با داشتن مدل HMM همان کلاس بهدست آوریم. این میزان احتمال برابر با نسبت شباهت کلی دنبالهٔ مشاهدات است و به صورت زیر محاسبه میشود.
با توجه به رابطه فوق در حالت کلی معیار ML به صورت زیر تعریف میشود.
اگر چه هیچ راه حل تحلیلی مناسبی برای مدل وجود ندارد که مقدار را ماکزیمم نماید، لیکن میتوانیم با استفاده از یک روال بازگشتی پارامترهای مدل را به شکلی انتخاب کنیم که مقدار ماکزیمم بهدست آید. روش Baum-Welch یا روش مبتنی بر گرادیان از جملهٔ این روشها هستند.
الگوریتم بام- ولش
این روش را میتوان به سادگی و با محاسبه احتمال رخداد پارامترها یا با محاسبه حداکثر رابطه زیر بر روی تعریف نمود.
یکی از ویژگیهای مخصوص این الگوریتم این است که همگرایی در آن تضمین شدهاست. برای توصیف این الگوریتم که به الگوریتم پیشرو- پسرو نیز معروف است، باید علاوه بر متغیرهای کمکی پیشرو و پسرو که قبلاً تعریف شدهاند، متغیرهای کمکی بیشتری تعریف شود. البته میتوان این متغیرها را در قالب متغیرهای پیشرو و پسرو نیز تعریف نمود.
اولین متغیر از این دست احتمال بودن در حالت i در زمان t و در حالت j در زمان t+1 است، که به صورت زیر تعریف میشود.
این تعریف با تعریف زیر معادل است.
میتوان این متغیر را با استفاده از متغیرهای پیشرو و پسرو به صورت زیر تعریف نمود.

متغیر دوم بیانگر احتمال پسین حالت i با داشتن دنباله مشاهدات و مدل مخفی مارکوف میباشد و به صورت زیر بیان میشود.
این متغیر را نیز میتوان در قالب متغیرهای پیشرو و پسرو تعریف نمود.
رابطه بین دو متغیر فوق به صورت زیر بیان میشود.
اکنون میتوان الگوریتم آموزش بام – ولش را با ماکزیمم کردن مقدار بهدستآورد. اگر مدل اولیهٔ ما باشد، میتوانیم متغیرهای پسرو و پیشرو و متغیرهای و را تعریف نمود. مرحلهٔ بعدی این است که پارامترهای مدل را با توجه به روابط بازتخمین زیر بهروزرسانی کنیم.
فرمولهای بازتخمین را میتوان بهراحتی به شکلی تغییر داد که با توابع چگالی پیوسته نیز قابل استفاده باشند.
الگوریتم حداکثرسازی امید ریاضی (Expectation Maximization)
الگوریتم حداکثرسازی امید ریاضی یا EM به عنوان یک نمونه از الگوریتم بام – ولش در آموزش مدلهای HMM مورد استفاده قرار میگیرد. الگوریتم EM دارای دو فاز تحت عنوان Expectation و Maximization است. مراحل آموزش مدل در الگوریتم EM به صورت زیر است.
- مرحله مقدار دهی اولیه: پارامترهای اولیه مدل را تعیین مینماییم.
- مرحله امید ریاضی(Expectation): برای مدل موارد زیر را محاسبه میکنیم.
- مقادیر با استفاده از الگوریتم پیشرو
- مقادیر و با استفاده از الگوریتم پسرو
- مرحله ماکزیممسازی (Maximization): مدل را با استفاده از الگوریتم باز تخمین محاسبه مینماییم.
- مرحله بروزرسانی
- بازگشت به مرحله امید ریاضی
روال فوق تا زمانی که میزان نسبت شباهت نسبت به مرحله قبل بهبود مناسبی داشته باشد ادامه مییابد.
روش مبتنی بر گرادیان
در روش مبتنی بر گرادیان هر پارامتر از مدلبا توجه به رابطه زیر تغییر داده میشود.
که در آن مقدار J با ید مینیمم شود. در این حالت خواهیم داشت.
از آنجا که مینیمم کردن J معادل است با مینیمم کردننیاز است است تا معیار ML بهینه بهدست آید. آنگاه مسئله، یافتن مقدار مشتق برای تمام پارامترهایاز مدل است. این کار را میتوان به سادگی با استفاده از مقدار
با مشتق گرفتن از رابطهٔ قبل به این نتیجه دست مییابیم:
از آنجا که در رابطهٔ فوق مقدار بر حسب بهدست میآید، میتوان رابطه بهدستآورد.
در روش مبتنی بر گرادیان، مقدار را باید برای پارامترهای (احتمال انتقال) و (احتمال مشاهدات) بهدستآورد.
استفاده از مدل HMM در شناسایی گفتار
بحث شناسایی اتوماتیک گفتار را میتوان از دو جنبه مورد بررسی قرار داد.
- از جنبه تولید گفتار
- از جنبه فهم و دریافت گفتار
مدل مخفی مارکوف (HMM) تلاشی است برای مدلسازی آماری دستگاه تولید گفتار و به همین دلیل به اولین دسته از روشهای شناسایی گفتار تعلق دارد. در طول چندین سال گذشته این روش به عنوان موفقترین روش در شناسایی گفتار مورد استفاده قرار گرفتهاست. دلیل اصلی این مسئله این است که مدل HMM قادر است به شکل بسیار خوبی خصوصیات سیگنال گفتار را در یک قالب ریاضی قابل فهم تعریف نماید.
در یک سیستم ASR مبتنی بر HMM قبل از آموزش HMM یک مرحله استخراج ویژگیها انجام میگردد. به این ترتیب ورودی HMM یک دنباله گسسته از پارامترهای برداری است. بردارهای ویژگی میتواند به یکی از دو طریق بردارهای چندیسازی شده یا مقادیر پیوسته به مدل HMM آموزش داده شوند. میتوان مدل HMM را به گونهای طراحی نمود که هر یک از این انواع ورودیها را دریافت نماید. مسئله مهم این است که مدل HMM چگونه با طبیعت تصادفی مقادیر بردار ویژگی سازگاری پیدا خواهد کرد.
استفاده از HMM در شناسایی کلمات جداگانه
در حالت کلی شناسایی واحدهای گفتاری جدا از هم به کاربردی اطلاق میشود که در آن یک کلمه، یک زیر کلمه یا دنبالهای از کلمات به صورت جداگانه و به تنهایی شناسایی شود. باید توجه داشت که این تعریف با مسئله شناسایی گفتار گسسته که در آن گفتار به صورت گسسته بیان میشود متفاوت است. در این بین شناسایی کلمات جداگانه کاربرد بیشتری به نسبت دو مورد دیگر دارد و دو مورد دیگر بیشتر در عرصه مطالعات تئوری مورد بررسی قرار میگیرند. برای این کاربرد راه حلهای مختلفی وجود دارد زیرا معیارهای بهینهسازی متفاوتی را برای این منظور معرفی شدهاست و الگوریتمهای پیادهسازی شده مختلفی نیز برای هر معیار موجود است. این مسئله را از دو جنبه آموزش و شناسایی مورد بررسی قرار میدهیم.
آموزش
فرض میکنیم که فاز پیش پردازش سیستم دنباله مشاهدات زیر را تولید نماید:
پارامترهای اولیه تمام مدلهای HMM را با یک مجموعه از مقادیر مشخص مقدار دهی مینماییم.
در آغاز این مسئله را برای حالت clamped در نظر بگیرید. از آنجایی که ما برای هر کلاس از واحدها یک HMM داریم، میتوانیم مدلاز کلاس l را که دنباله مشاهدات فعلی به آن مربوط میشود، را انتخاب نماییم.
برای حالت free نیز به مانند حالت قبل میتوان مقدار نسبت شباهت را بهدستآورد.
که در آن بیانگر میزان شباهت دنبالهٔ مشاهدات فعلی به کلاس l در مدل است.
شناسایی
در مقایسه با آموزش، روال شناسایی بسیار سادهتر است. الگوریتم دنبالهٔ مشاهدات موردنظر را دریافت میکند.
در این حالت نرخ شناسایی به صورت نسبت بین واحدهای شناسایی صحیح به کل واحدهای آموزشی حساب میشود.
برای دریافت اطلاعات بیشتر فایل زیر را دانلود و مشاهده فرمایید.
رمز فایل: behsanandish.com
ML_93_1_Chap15_Hidden Markov Model
مدل مخفی مارکوف (Hidden Markov Model) قسمت 1
مدل مخفی مارکوف (Hidden Markov Model) قسمت 2
مدل مخفی مارکوف (Hidden Markov Model) قسمت 3
مدل مخفی مارکوف (Hidden Markov Model) قسمت 4





![{\displaystyle \delta _{t+1}(j)=b_{j}(o_{t+1})[max\delta _{t}(i)a_{ij}],\qquad 1\leq i\leq N,\qquad 1\leq t\leq T-1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/341a45475d2d12accb08d82f405386c59e4075f8)










![{\displaystyle \ Q(\lambda ,{\bar {\lambda }})=\sum _{q}p\{q|O,\lambda \}log[p\{O,q,{\bar {\lambda }}\}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a669bd0b99c6cb8b0638b6cea62136faf6886442)




![{\displaystyle \gamma _{t}(i)=\left[{\frac {\alpha _{t}(i)\beta _{t}(i)}{\sum _{i=1}^{N}\alpha _{t}(i)\beta _{t}(i)}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/208320604d962f63ab6c3b1f4c30f35fafd0371c)












![{\displaystyle \ \Theta ^{new}=\Theta ^{old}-\eta \left[{\frac {\partial j}{\partial \Theta }}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b0046e064301e13c53db6ae1b74307db96cadd2)











![{\displaystyle \ L_{tot}^{free}=\sum _{m=1}^{N}L_{m}^{I}=\sum _{m=1}^{N}[\sum _{i\in \lambda _{m}}\alpha _{t}(i)\mathrm {B} _{t}(i)]\sum _{m=1}^{N}\sum _{i\in \lambda _{i}}\alpha _{T}(i)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/48e2d5288de6f92113a9fd886bb4cb6d940ecb4e)





دیدگاه خود را ثبت کنید
تمایل دارید در گفتگوها شرکت کنید؟در گفتگو ها شرکت کنید.