زنجیره مارکوف (Markov Approach modeling) قسمت 1
زنجیره مارکوف مدلی تصادفی برای توصیف یک توالی از رویدادهای احتمالی است که در آن احتمال هر رویداد فقط به حالت رویداد قبلی بستگی دارد. زنجیره مارکوف که به افتخار آندری مارکوفریاضیدان اهل روسیه این گونه نامگذاری شده یک سیستم ریاضی است که در آن انتقال میان حالات شمارا، از حالتی به حالت دیگر صورت میگیرد. زنجیره مارکوف یک فرایند تصادفی بدون حافظهاست بدین معنی که توزیع احتمال شرطی حالت بعد تنها به حالت فعلی بستگی دارد و مستقل از گذشتهٔ آن است. این نوع بدون حافظه بودن خاصیت مارکوف نام دارد. زنجیره مارکوف درمدلسازی دنیای واقعی کاربردهای زیادی دارد.
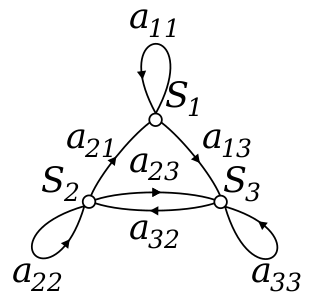
نمونهای از زنجیره مارکوف با سه حالت
معرفی
زنجیره مارکوف (Markov Approach modeling) یک فرایند تصادفی گسسته در زمان با خاصیت مارکوف است. اگرچه برخی از نویسندگان در مورد فرایندهای پیوسته در زمان هم از اصطلاح زنجیره مارکوف استفاده میکنند. یک فرایند تصادفی گسسته در زمان شامل سیستمی است که در هر مرحله در حالت خاص و مشخصی قرار دارد و به صورت تصادفی در هر مرحله تغییر حالت میدهد. مراحل اغلب به عنوان لحظههای زمانی در نظر گرفته میشوند ولی میتوان آنها را فاصله فیزیکی یا هر متغیر گسسته دیگری در نظر گرفت. خاصیت مارکوف بیان میکند که توزیع احتمال شرطی برای سیستم در مرحله بعد فقط به حالت فعلی سیستم بستگی دارد و به حالتهای قبل بستگی ندارد. چون سیستم به صورت تصادفی تغییر میکند بهطور کلی پیشبینی حالت زنجیره مارکوف در نقطهای خاص در آینده غیرممکن است. با این حال ویژگیهای آماری سیستم در آینده قابل پیشبینی است که در بسیاری از کاربردها همین ویژگیهای آماری بسیار حائز اهمیت است.
تغییرات حالات سیستم انتقال نام دارند و احتمالهایی که به این تغییر حالتها نسبت داده میشوند احتمال انتقال نام دارند. یک فرایند مارکوف با یک فضای حالت شمارا، یک ماتریس گذار برای توصیف احتمالهای هر انتقال و یک حالت اولیه (یا توزیع اولیه) در فضای حالت مشخص میشود. اگر فضای حالت متناهی باشد زنجیر مارکوف را زنجیر مارکوف متناهی یا زنجیر مارکوف با فضای حالت متناهی میگوییم و اگر نامتناهی باشد زنجیر مارکوف را زنجیر مارکوف نامتناهی یا زنجیر مارکوف با فضای حالت نامتناهی میگوییم. طبق قرار داد، فرض میکنیم همیشه حالت بعدی وجود دارد و در نتیجه فرایند تا ابد ادامه پیدا میکند.
یکی از معروفترین زنجیرههای مارکوف که موسوم به «پیادهروی می خواره» است یک پیادهروی تصادفی است که در آن در هر قدم موقعیت با احتمال برابر به اندازه ۱+ یا ۱- تغییر میکند. در هر مکان دو انتقال ممکن وجود دارد یکی به عدد صحیح بعدی(۱+) و یکی به عدد صحیح قبلی(۱-). احتمال هر انتقال فقط به حالت کنونی بستگی دارد. برای مثال احتمال انتقال از ۵ به ۶ برابر با احتمال انتقال از ۵ به ۴ است و هر دوی این احتمالات برابر با ۰٫۵ هستند. این احتمالات مستقل از حالت قبلی (که یا ۴ بوده یا ۶) هستند.
مثالی دیگر عادات غذایی موجودی است که فقط انگور، پنیر و کاهو میخورد و عادات غذایی او از قوانین زیر پیروی میکند:
- او فقط یک بار در روز غذا میخورد.
- اگر امروز پنیر بخورد فردا انگور یا کاهو را با احتمال برابر خواهد خورد.
- اگر امروز انگور بخورد فردا با احتمال ۰٫۱ انگور، با احتمال ۰٫۴ پنیر و با احتمال ۰٫۵ کاهو خواهد خورد.
- اگر امروز کاهو بخورد فردا با احتمال ۰٫۴ انگور و با احتمال ۰٫۶ پنیر خواهد خورد.
عادات غذایی این موجود را میتوان با یک زنجیره مارکوف مدلسازی کرد به دلیل این که چیزی که فردا میخورد (حالت بعدی) تنها به چیزی که امروز خوردهاست (حالت فعلی) بستگی دارد. یکی از ویژگیهای آماری که میتوان در مورد این زنجیره محاسبه کرد امید ریاضی درصد روزهایی است که انگور خوردهاست (در یک دوره طولانی).
مثالهایی از زنجیره مارکوف
ورشکستگی قمارباز
ورشکستگی قمارباز مسئلهای معروف از زنجیره مارکوف است. در این مسئله دو فرد تاس میاندازند و هر بار که سکه شیر آمد شخص A یک دلار از B میبرد و هر بار سکه خط بیاید، شخص B یک دلار از A میبرد. در ابتدای بازی A مقدار a دلار و B مقدار b دلار دارد. فرض کنید Xi دارایی A پس از i مرحله بازی باشد. یکی از خواص دنباله {Xi} این است که اگر در مرحلهٔ nام مقدار Xi را بدانیم در این صورت سرمایه A از آن مرحله به بعد تنها به Xn و نه به X0, X1, …, Xn-1 وابسته است. یعنی اگر سرمایهٔ A در زمان حال معلوم باشد، سرمایهٔ آیندهٔ او مستقل از پولی است که در هر مرحله از بازی در گذشته برنده شده یا باختهاست.
فرایند زاد مرگ
اگر صد دانه ذرت در فری قرار دهیم، هر دانه در زمانی مستقل که از توزیع نمایی پیروی میکند، منفجر میشود. این مثالی از زنجیره زمان پیوسته مارکوف است. اگر Xt نشاندهنده تعداد دانههای ذرتی باشد که تا زمان t منفجر شدهاند، مسئله را میتوان به صورت تعداد دانههایی که بعد از t منفجر میشوند مطرح نمود. دانستن زمان انفجار دیگر دانهها اهمیتی ندارد و تنها دانستن تعداد دانههایی که تا کنون منفجر شدهاند کافیست. فرایند شرح داده شده در اینجا، تقریبی از یک فرایند پواسونی است. در حالت کلی فرایندهای پواسون نیز فرایند مارکوف هستند.
بازیهای تختهای با تاس
بازی مار و پله یا هر بازی دیگری که حرکات با تاس تعیین میشود یک زنجیرهٔ مارکوف هستند. این نوع بازیها در نقطه مقابل بازیهای کارتی مانند blackjack هستند که کارتها مانند حافظهٔ حرکت قبلی عمل میکنند. برای درک این تفاوتها احتمال یک حرکت مشخص را در بازی در نظر بگیرید. در بالا به بازیهایی که با تاس بازی میشوند اشاره کردیم، تنها چیزی که اهمیت دارد حالت کنونی روی تخته است. حالت بعدی روی تخته به حالت کنونی و چرخش بعدی تاس بستگی دارد و وابسته به اینکه که مهرهها چگونه در حالت کنونی قرار گرفتهاند، نیست. در بازی مانند blackjack، بازیکن میتواند با به خاطر سپردن این که کدام کارتها تاکنون نشان داده شدهاند، برتری کسب کنند؛ بنابراین حالت بعدی بازی مستقل از حالت کنونی نیست.
گامهای تصادفی متمایل به مرکز
یک حرکت تصادفی روی تعدادی خط را در نظر بگیرید، موقعیت کنونی (که x نامیده مینامیم) با احتمالات زیر میتواند به +۱ (به راست) یا -۱(به چپ) تغییر کند:
(c یک عدد ثابت بزرگتر از ۰ است)
به عنوان مثال اگر عدد ثابت c برابر ۱ باشد، احتمال حرکت به چپ از موقعیت x=-۲,-۱٬۰٬۱٬۲ به ترتیب برابرست با:.
یک گام تصادفی یک اثر مرکزی دارد بهطوریکه با افزایش تضعیف c میشود. از آنجایی که احتمالات تنها به وضعیت کنونی بستگی دارد (مقدار x) و وابسته به هیچیک از موقعیتهای قبلی نیست، این گام تصادفی متمایل به مرکز در تعریف زنجیرهٔ مارکوف صدق میکند.
یک مدل آب و هوایی بسیار ساده

احتمال وضعیت آب و هوایی که آب و هوا در طول روز را نشان میدهد و هم به صورت بارانی و هم آفتابی مدل میشود، توسط یک ماتریس انتقال ارائه داده میشود. ماتریس P یک مدل آب و هوایی را نشان میدهد بهطوریکه روز بعد یک روز آفتابی، با احتمال %۹۰ آفتابی است و روز بعد یک روز بارانی، با احتمال %۵۰ آفتابی است. ستونها و سطرها با آفتابی و بارانی برچسبگذاری میشوند.
(P)i j احتمال این است که هوای امروز از نوع i باشد و فردا از نوع j باشد.
در نظر داشته باشید که حاصل جمع احتمالات سطر P برابر ۱ است.
حالت ثابت آب و هوا
در این مثال، پیشبینی هوا در روزهای دور از هم غلط از آب در میآید و متمایل به بردار حالت پایدار است. این بردار احتمال هوای آفتابی و بارانی را در همهٔ روزها نشان میدهد و مستقل از آب وهوای اولیه است.
بردار حالت ثابت به این صورت تعریف میشود:
ولی تنها زمانی به یک مقدار منظم همگراست که p یک ماتریس انتقال منظم باشد (بعبارت دیگر حداکثر یک Pn با ورودیهای غیر صفر وجود دارد)
از آنجایی که q مستقل از شرایط اولیه است، زمانی که بوسیلهٔ P ترجمه میشود، بایستی بدون تغییر بماند؛ که این باعث میشود که q تبدیل به بردار ویژه شود، به این معنی که از P مشتق شود. برای مثال آب و هوا:
پس و از آنجایی که این دو بردار احتمال هستند، داریم
حل این دو معادله یک توزیع حالت یکنواخت را میدهد:
در نتیجه %۸۳ روزها آفتابی است.
زنجیره مارکوف (Markov Approach modeling) قسمت 1
زنجیره مارکوف (Markov Approach modeling) قسمت 2
زنجیره مارکوف (Markov Approach modeling) قسمت 3
زنجیره مارکوف (Markov Approach modeling) قسمت 4
زنجیره مارکوف (Markov Approach modeling) قسمت 5








دیدگاه خود را ثبت کنید
تمایل دارید در گفتگوها شرکت کنید؟در گفتگو ها شرکت کنید.