ماشین تورینگ چیست ؟ قسمت 3
به همین دلیل، از لحاظ منطق و معماری، بیشتر کامپیوترهای امروزی از نوادگان مستقیم ماشین تورینگی هستند که از تجهیزات بهجا مانده از جنگ در ساختمانی واقع در مزرعهای در نیوجرسی ساخته شده بود. تورینگ و فون نویمان نخستینبار یکدیگر را در سال 1935 در کمبریج ملاقات کردند و پس از آن به مدت دو سال در دانشگاه پرینستون در کنار یکدیگر بودند. جایی که نیومن برای مدت شش ماه به آنها ملحق شد و در کنار یکدیگر به تحصیل و تبادل نظر پرداختند.
اینکه فن نویمان و تورینگ تا چه حد در زمان جنگ با یکدیگر همکاری داشتهاند، چندان معلوم نيست، اما چیزی که مشخص است آن است که تورینگ از نوامبر 1942 تا مارس 1943 در امریکا حضور داشته است در حالی که فون نویمان از فوریه تا جولای 1943 در انگلیس بوده است. در طی جنگ، فیزیکدانان انگلیسی با همکاری فون نویمان، همکاریهای بسیار مهمی را در پروژه بمب اتمی در Los Alamos در نیومکزیکو به انجام رساندند. در عین حال، تحلیلگران رمز امریکایی، در انجام تلاشهای رمزگشایی انگلیس به همکاری با تورینگ پرداختند. با اینکه تورینگ، فوننویمان و نیومن نمیتوانستند آزادانه با هم مکاتبه کنند اما شاید ایدههایشان را در خلال و پس از اتمام جنگ بهصورت شفاهی با یکدیگر در میان گذاشتهاند. مدل تورینگ یک مدل یک بعدی بود که رشتهای از علامتها را روی یک نوار کاغذی در نظر میگرفت در حالی که پیادهسازی فون نویمان یک مدل دو بعدی به شمار میآمد؛ یک ماتریس با آدرس دسترسی تصادفی که در بیشتر کامپیوترهای امروزی نیز وجود دارد. اینترنت- مجموعهای از ماشینهای به هم پیوسته تورینگ که به یک نوار مشترک دسترسی دارند- چشمانداز مدل مربوطه را سه بعدی کرد و هنوز، روش کار کامپیوترها از سال 1946 تاکنون بیتغییر باقی مانده است.
تورینگ و نویمان از وجود خطا در ماشینهایشان مطلع بودند. با اینکه کدهای آن زمان به سادگی قابل اشكالزدايي بودند، اما سختافزار به شدت غیرقابل اطمینان بود و نتایجی بیثبات ارائه میکرد. مشکلی که اکنون کاملاً برعکس شده است. هردوی آنها میدانستند که سیستمهای بیولوژیک روی متدهای آماری و مقاوم در برابر خطا برای پردازش متمرکز شدهاند (سیستمهایی نظیر کدگذاری فرکانسی پالسها در مغز) و فرض کردند که فناوری نیز باید از همین روند پیروی کند. به اعتقاد فون نویمان، اگر هر خطا گرفته شده، تبیین میشد و سپس تصحیح میشد، سیستمی به پیچیدگی ارگانیسمهای زنده نمیتوانستند پاسخهایی در حد میلیثانیه داشته باشند. به اعتقاد تورینگ نیز اگر باید ماشینی بیخطا باشد، پس نمیتواند هوشمند نیز باشد. وقتی تورینگ در سال 1948به گروه نیومن در دانشگاه منچستر که مشغول طراحی Manchester Mark 1 بودند پیوست، یک تولیدکننده عدد تصادفی در آن گنجاند که اجازه میداد کامپیوتر حدس زده و از اشتباهات خود درس بگیرد. لازم به ذکر است که Manchester Mark 1، نمونه اولیه Ferranti Mark 1 بود که نخستین کامپیوتر دیجیتالی با برنامه ذخیره شده به شمار میآمد.
با اینکه ماشین جامع با قطعیت تورینگ بیشترین توجهها را به سوی خود جلب کرد، ایده ماشینهای بدون قطعیتِ پیشگوی وی به اساس کار هوش نزدیکتر بود؛ شهود و بینش، پرکننده فاصله میان عبارات منطقی است. ماشینهای پیشگوی تورینگ امروزه دیگر مفاهیم مجرد نظري نیستند چراکه موتورهای جستوجوی اینترنت مثال خوبی از وجود آنها بهشمار ميآيند. یک موتور جستوجو در حالت عادی بهصورت قطعیتی (deterministic) کار میکند تا زمانی که کاربری روی یک لینک کلیک میکند. از این طریق، کاربر بهطور غیرقطعی (non-deterministic)، مکان اطلاعات سودمند و پر ارزش را به نقشه دادهای موتور جستوجو اضافه میکند.
تورینگ میخواست بداند که چگونه مولکولها میتوانستند بهطور مجموعهای خود را سازماندهی کرده یا اینکه آیا ماشین میتواند فکر کند یا خیر؟ فون نویمان میخواست بداند که مغز چگونه کار میکند و آیا ماشینها میتوانند خود را بازتولیدکنند؟ تورینگ که در سن 41 سالگی درگذشت، یک نظريه ناتمام در زمینه Morphogenesis (تکوینِ ترکیب) از خود بهجای گذاشت و فون نویمان نیز که در سن 53 سالگی درگذشت، یک تئوری ناتمام در زمینه خود بازتولیدی (مدلی که براساس برداشتی از توانایی ماشین تورینگ از تولید کپیهایی از خود شکل گرفته بود) از خود بهجای گذارد. اگر هردوی آنها مدت طولانیتری زنده میماندند و ایدههای آن دو با یکدیگر ترکیب میشد، نتایج جالب و شگفتانگیزی میتوانست رقم بخورد. زندگی آنها به فاصله بسیار کوتاهی از کشف مکانیزم درونی ترجمه بین توالی و ساختار در بیولوژی به اتمام رسید و اگر آنها از این کشف مطلع میشدند، چه نوآوریهای خارقالعادهای را میتوانستند به ارمغان بیاورند!
بخش دوم
ماشین تورینگ
ماشین تورینگ دستگاهی است که براساس قواعدی که در یک جدول آورده شده، علامتهای نوشته شده روی یک نوار کاغذی را خوانده و براساس توالی آنها، محاسباتی را انجام میدهد. با وجود سادگی، این ماشین میتواند منطق هر الگوریتم کامپیوتری را شبیهسازی کرده و به طور خاص، یک مثال خوب در توضیح عملکرد پردازندههای مرکزی درون کامپیوترها به شمار میآید.
این ماشین نخستینبار توسط آلن تورینگ در سال 1936 و در قالب یک مقاله، در پاسخ به مسئلهای که ریاضیدان آلمانی، دیوید هیلبرت منتشر کرده بود، مطرح شد. مسئله هیلبرت تصمیمگیری درباره این بود که آیا یک روال مشخص وجود دارد که بتواند صحت یک عبارت منطقی را در مراحلی متناهی محاسبه کند یا خیر؟ وی برای پاسخگویی به این سؤال، چنین ماشینی را تصور کرد و در نهایت به پاسخ منفی برای مسئله هیلبرت دست یافت. در اکتبر همان سال، فردی به نام امیل پست (Emil Post) مقالهای با عنوان «Finite combinatory processes – formulation 1» منتشر کرد که در آن به توضیح و تبیین نوعی ماشین پرداخته شده بود که میتوان آن را نوع خاصی از ماشین تورینگ به شمار آورد. کار وی مستقل از تورینگ انجام شده بود با این تفاوت که ماشین پست از الفبای باینری استفاده میکرد و مفاهیم حافظه ماشین وی حالت مجردتری نسبت به تصورات تورینگ داشت. به همین جهت، گاهی به این چنین ماشینهایی پست-تورینگ (Post-Turing Machines) نیز گفته میشود. بر این اساس، باید توجه داشت که ماشین تورینگ یک فناوری محاسباتی عملی به شمار نمیآید بلکه یک دستگاه مجازی و نظری برای نمایش یک ماشین محاسباتی است. ماشین تورینگ، مثال خوبی برای دانشمندان کامپیوتر در زمینه درک کامل محدودیتهای محاسبات مکانیکی است.
در اصل، ماشین تورینگ برای مدلسازی کامپیوتر کاربرد ندارد، بلکه هدف اصلی آن مدلسازی خود مفهوم محاسبات است.
تورینگ بعدها و در سال 1948 در مقالهای با عنوان ساز و كار رايانش (Computing Machinery and Intelligent)، تعریف دقیقتری از ماشین خودکار محاسباتی خود ارائه کرد و نام آن را ماشین محاسبات منطقی گذارد. وی در این مقاله چنین میگوید:
«… یک ظرفیت بینهایت حافظه که بهصورت نواری کاغذی با طول بینهایت و تقسیم شده به مربعهای مساوی که روی هرکدام امکان نوشتن علامتهایی وجود دارد. در هر لحظه، یک علامت در ماشین قرار میگیرد که علامت اسکن شده نامیده میشود. ماشین میتواند علامت مذکور را تغییر داده و در اصل، رفتار آن برگرفته از همان علامت است و دیگر علامتهای موجود روی نوار نمیتوانند تأثیری روی عملکرد ماشین بگذارند. نوار کاغذی میتواند به عقب و جلو حرکت کرده و این یکی از اصول اولیه کاری ماشین خواهد بود…»
ماشین تورینگ در اصل تشکیل یافته از چند عنصر اصلی است که عبارتند از:
نوار: که به بخشهای کوچک مربع شکلی به نام سلول تقسیم شده و هرکدام میتواند حاوی یک علامت از یک الفبای محدود باشد. این نوار به طور دلخواه از سمت چپ یا راست نامتناهی بوده و توسط ماشین به راحتی جابهجا میشود. در بعضی از مدلها، سمت چپ نوار با علامتی مشخص نشانهگذاری شده و نوار تنها به سمت راست نامتناهی در نظر گرفته میشود.
هد (Head): که برای خواندن و نوشتن علامتهای روی نوار و انجام عملیات انتقال نوار به چپ یا راست مورد استفاده قرار میگیرد. در برخی مدلها هد متحرک بوده و نوار ثابت است.
جدول متناهی دستورالعملها: که در برخی مواقع جدول عملکرد یا تابع گذار نامیده میشود، جدولی حاوی دستورالعملهایی پنجگانه یا چهارگانه با فرمت qiaj→qi1aj1dk است که وظیفه تعیین عملکرد ماشین در برابر علامتهای روی نوار را بر عهده دارد. متغیرهای آورده شده در عبارت بالا، نشاندهنده حالت جاری ماشین، علامت خواندهشده، میزان جابهجایی هد و… هستند.
ثبات حالت: حالت ماشین تورینگ را که از میان تعداد متناهی حالت مختلف انتخاب میشود، ذخیره میکند. همیشه یک حالت اولیه برای ماشین در زمان راهاندازی در این رجیستر ذخیره میشود. تورینگ معتقد بود که این رجیستر، جایگزین حالت ذهنی شخصی است که عملیات محاسبات را به انجام میرساند. توجه کنید که هر جزء ماشین، یعنی حالتها و علامتها و همچنین هر عملکرد ماشین یعنی چاپ، پاککردن و حرکت دادن نوار متناهی، گسسته و قابل جداسازی بوده و میزان حافظه در دسترس آن یعنی نوار کاملاً نامتناهی است. یکی از مواردی که امکان دارد پیچیدگی خاصی در بر داشته باشد، state یا حالت ماشین است که میتوان دو برداشت مختلف از آن داشت. بسیاری از افرادی که پس از تورینگ به مباحثه درباره ماشین وی پرداختهاند از عبارت حالت برای اشاره به نام یا مشخصکردن دستورالعملی که باید اجرا شود (مانند محتویات رجیستر حالت) استفاده کردهاند اما تورینگ در سال 1936 یک تفاوت کاملاً آشکار میان رکوردهای پیکربندی یا حالات درونی ماشین با حالت پیشرفت آن در روال محاسبات قائل بود و به همین دلیل، فرمول حالت وی حاوی دستورالعمل جاری به همراه کلیه علامتهای روی نوار در نظر گرفته شده بود.
بعدها و در سال 1979، مفهوم ماشین تورینگ توسط هاپ کرافت (Hopcroft) و اولمن براساس پیشرفتهای حاصل شده، به طور کاملاً مناسب و بهصورت هفت گانه و بر اساس <M=<Q,Γ,b,Σ,δ,q0,F فرمولبندی و منظم شد که در آن متغیرهای مورد استفاده به ترتیب نشان از مجموعه حالات سیستم (Q)، الفبای استفاده شده روی نوار(Γ)، علامت نشانگر فضای خالی(b)، مجموعه علامات ورودی (Σ)، جدول گذار حالتها(δ)، حالت اولیه (q0 ) و حالتهای نهایی قابل قبول (F ) دارند. هر چیزی که با این مفهوم قابل توصیف باشد، یک ماشین تورینگ به شمار میآید. مثالی در این زمینه، ماشین Busy Beaver معروف است که برای رسیدن به بیشینه درگیری عملیاتی در میان ماشینهای تورینگ موجود در یک کلاس مشخص مطرح شده و مورد استفاده قرار میگیرد. توصیف این ماشین بر اساس مدلسازی مطرح شده در بالا چنین خواهد بود:
{Q = { A, B, C, HALT
{Γ = { 0, 1
«تهی»=b=o
{Σ = {1
جدول 1= δ
حالت اولیه = q0 = A
مجموعه حالت تک عضوی {F = {HALT
در کنار انواع نمونههای سختافزاری ساخته شده، پیادهسازیهای رایانهای مختلفی از ماشین تورینگ وجود دارد که با سر زدن و مشاهده روند کاری آنها، میتوانید به خوبی با نحوه کار ماشین تورینگ آشنا شوید. یکی از این ماشینهای شبیهسازی شده که اتفاقاً سادهترین و معمولیترین آنها نیز به شمار میآید در آدرسwww.turing.org.uk/turing/scrapbook/tmjava.html وجود دارد و از طریق یک مرورگر معمولی قابل دسترسی است. در این ماشین، میتوانید عملیات مربوطه را انتخاب کرده و با زدن Load دادههای مربوطه را روی نوار نوشته و سپس با زدن Run نتیجه اجرای عملیات روی نوار مذکور را ببینید. (شکل1)
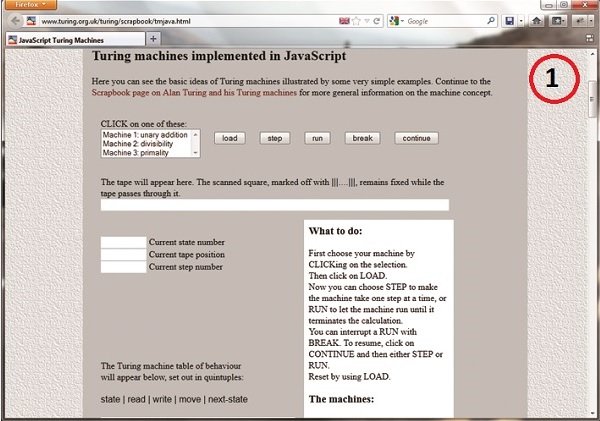
مثال قبل، نمونه چندان خوبی برای درک شهودی عملکرد ماشین تورینگ نیست چرا که عملیات خود را به یکباره و سریع انجام میدهد.
در نقطه مقابل، نمونه پیادهسازی شده در آدرس http://ironphoenix.org/tril/tm/ عملکرد بصری مناسبی داشته و با رعایت انجام با فاصله عملیات، درک بهتری از کارکرد ماشین تورینگ با برنامه های مختلف را ارائه میکند. (شکل2)

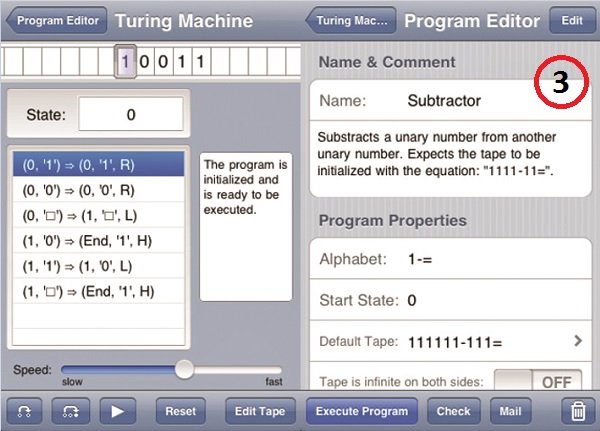
یک نمونه جالب دیگر از شبیهسازیهای نرمافزاری از ماشینهای تورینگ، شبیهسازی مخصوص iOS آن است که از طریق فروشگاه App Store قابل دانلود است. این برنامه، علاوه بر اجرای عملیات ماشین تورینگ بهصورت بصری، برنامههای پیشفرض و همچنین قابل ویرایشی را نیز به همراه توضیحات کاملی از عملکرد هرکدام در اختیارکاربر میگذارد. (شکل3)
جدول گذار حالتهای این ماشین که برای 2 علامت و 3 حالت طراحی شده، در جدول 1 آورده شده است. در این جدول علامت P به معنای چاپ یک روی نوار بوده و L و R به ترتیب به معنای انتقال نوار به چپ و راست است. این جدول را میتوان بهصورت دیاگرام انتقال حالت نیز نشان داد. اگرچه جدولهای بزرگ انتقال حالت بهتر است بهصورت جدولی باقی بمانند و این گونه قابلیت فهم بالاتری دارند، با این حال نمایش وضعیت ماشینهای ساده بهصورت دیاگرامی میتواند درک بهتر و سادهتری از آنها را ارائه کند. توجه داشته باشید که دیاگرامهای انتقال حالت، یک تصویر فریزشده از جدول عملکرد ماشین در زمان است و نباید آن را منحنی عملکرد محاسبات ماشین در طول زمان و مکان دانست. شکل 1 نمایی از دیاگرام انتقال حالت ماشین سه حالته Busy Beaver را نشان میدهد. با این حال، هر بار که ماشین Busy Beaver شروع به کار میکند، یک منحنی عملکردی را از آغاز تا پایان میپیماید اما یک ماشین کپیکننده که میتواند پارامترهای ورودی متغیر داشته باشد، ممکن است منحنی متفاوتی را طی کند. برای تعیین نحوه عملکرد صحیح یک ماشین در طول زمان به سادگی میتوان از دیاگرام پیشرفت محاسبات استفاده کرد که نمونهای از آن برای ماشین 3 حالته Busy Beaver در شکل 2 آورده شده است.

ماشین تورینگ چیست ؟ قسمت 1
ماشین تورینگ چیست ؟ قسمت 2
ماشین تورینگ چیست ؟ قسمت 3



دیدگاه خود را ثبت کنید
تمایل دارید در گفتگوها شرکت کنید؟در گفتگو ها شرکت کنید.