الگوریتم کلونی مورچه ها یا ACO همانطور که میدانیم مسئله یافتن کوتاهترین مسیر، یک مسئله بهینه سازیست که گاه حل آن بسیار دشوار است و گاه نیز بسیار زمانبر. برای مثال مسئله فروشنده دوره گرد را نیز میتوان مطرح کرد. در این روش(ACo)، مورچههای مصنوعی بهوسیلهٔ حرکت بر روی نمودار مسئله و با باقی گذاشتن نشانههایی بر روی نمودار، همچون مورچههای واقعی که در مسیر حرکت خود نشانههای باقی میگذارند، باعث میشوند که مورچههای مصنوعی بعدی بتوانند راهحلهای بهتری را برای مسئله فراهم نمایند. همچنین در این روش میتوان توسط مسائل محاسباتی-عددی بر مبنای علم احتمالات بهترین مسیر را در یک نمودار یافت.
روش که از رفتار مورچهها در یافتن مسیر بین محل لانه و غذا الهام گرفته شده؛ اولین بار در ۱۹۹۲ توسط مارکو دوریگو (Marco Dorigo) در پایان نامهٔ دکترایش مطرح شد.
مقدمه
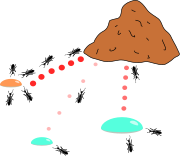
الگوریتم کلونی مورچه الهام گرفته شده از مطالعات و مشاهدات روی کلونی مورچه هاست. این مطالعات نشان داده که مورچهها حشراتی اجتماعی هستند که در کلونیها زندگی میکنند و رفتار آنها بیشتر در جهت بقاء کلونی است تا درجهت بقاء یک جزء از آن. یکی از مهمترین و جالبترین رفتار مورچهها، رفتار آنها برای یافتن غذا است و بویژه چگونگی پیدا کردن کوتاهترین مسیر میان منابع غذایی و آشیانه. این نوع رفتار مورچهها دارای نوعی هوشمندی تودهای است که اخیراً مورد توجه دانشمندان قرار گرفته است در دنیای واقعی مورچهها ابتدا به طور تصادفی به این سو و آن سو میروند تا غذا بیابند. سپس به لانه بر میگردند و ردّی از فرومون (Pheromone) به جا میگذارند. چنین ردهایی پس از باران به رنگ سفید در میآیند و قابل رویت اند. مورچههای دیگر وقتی این مسیر را مییابند، گاه پرسه زدن را رها کرده و آن را دنبال میکنند. سپس اگر به غذا برسند به خانه بر میگردند و رد دیگری از خود در کنار رد قبل میگذارند؛ و به عبارتی مسیر قبل را تقویت میکنند. فرومون به مرور تبخیر میشود که از سه جهت مفید است:
- باعث میشود مسیر جذابیت کمتری برای مورچههای بعدی داشته باشد. از آنجا که یک مورچه در زمان دراز راههای کوتاهتر را بیش تر میپیماید و تقویت میکند هر راهی بین خانه و غذا که کوتاهتر (بهتر) باشد بیشتر تقویت میشود و آنکه دورتر است کمتر.
- اگر فرومون اصلاً تبخیر نمیشد، مسیرهایی که چند بار طی میشدند، چنان بیش از حد جذّاب میشدند که جستجوی تصادفی برای غذا را بسیار محدود میکردند.
- وقتی غذای انتهای یک مسیر جذاب تمام میشد رد باقی میماند.
لذا وقتی یک مورچه مسیر کوتاهی (خوبی) را از خانه تا غذا بیابد بقیهٔ مورچهها به احتمال زیادی همان مسیر را دنبال میکنند و با تقویت مداوم آن مسیر و تبخیر ردهای دیگر، به مرور همهٔ مورچهها هم مسیر میشوند. هدف الگوریتم مورچهها تقلید این رفتار توسط مورچههایی مصنوعی ست که روی نمودار در حال حرکت اند. مسئله یافتن کوتاهترین مسیر است و حلالش این مورچههای مصنوعی اند.
از کابردهای این الگوریتم، رسیدن به راه حل تقریباً بهینه در مسئله فروشنده دورهگرد است. به طوری که انواع الگوریتم کلونی مورچهها برای حل این مسئله تهیه شده. زیرا این روش عددی نسبت به روشهای تحلیلی و genetic در مواردی که نمودار مدام با زمان تغییر کند یک مزیت دارد؛ و آن این که الگوریتمی ست با قابلیت تکرار؛ و لذا با گذر زمان میتواند جواب را به طور زنده تغییر دهد؛ که این خاصیت در روتینگ شبکههای کامپیوتری و سامانه حمل و نقل شهری مهم است.
در مسئله فروشنده دوره گرد باید از یک شهر شروع کرده، به شهرهای دیگر برود و سپس به شهر مبدأ بازگردد بطوریکه از هر شهر فقط یکبار عبور کند و کوتاهترین مسیر را نیز طی کرده باشد. اگر تعداد این شهرها n باشد در حالت کلی این مسئله از مرتبه (n-1)! است که برای فقط ۲۱ شهر زمان واقعاً زیادی میبرد:
روز۱۰۱۳*۷/۱ = S۱۰۱۶*۴۳۳/۲ = ms۱۰*۱۰۱۸*۴۳۳/۲ =!۲۰
با انجام یک الگوریتم برنامه سازی پویا برای این مسئله، زمان از مرتبه نمایی بدست میآید که آن هم مناسب نیست. البته الگوریتمهای دیگری نیز ارائه شده ولی هیچکدام کارایی مناسبی ندارند. ACO الگوریتم کامل و مناسبی برای حل مسئله TSP است.
مزیتهای الگوریتم کلونی مورچه ها
<تبخیر شدن فرومون> و <احتمال-تصادف>به مورچهها امکان پیدا کردن کوتاهترین مسیر را میدهد. این دو ویژگی باعث ایجاد انعطاف در حل هرگونه مسئله بهینهسازی میشوند. مثلاً در گراف شهرهای مسئله فروشنده دوره گرد، اگر یکی از یالها (یا گرهها) حذف شود الگوریتم این توانایی را دارد تا به سرعت مسیر بهینه را با توجه به شرایط جدید پیدا کند. به این ترتیب که اگر یال (یا گرهای) حذف شود دیگر لازم نیست که الگوریتم از ابتدا مسئله را حل کند بلکه از جایی که مسئله حل شده تا محل حذف یال (یا گره) هنوز بهترین مسیر را داریم، از این به بعد مورچهها میتوانند پس از مدت کوتاهی مسیر بهینه (کوتاهترین) را بیابند.
کاربردهای الگوریتم کلونی مورچه ها
از کاربردهای الگوریتم کلونی مورچه ها میتوان به بهینه کردن هر مسئلهای که نیاز به یافتن کوتاهترین مسیر دارد، اشاره نمود:
۱. مسیر یابی داخل شهری و بین شهری.
۲. مسیر یابی بین پستهای شبکههای توزیع برق ولتاژ بالا.
۳. مسیر یابی شبکههای کامپیوتری. ۴-استفاده ازوب. ۵-استفاده ازACOدربهینه سازی شبکههای توزیع آب و…
الگوریتم
پروسهٔ پیدا کردن کوتاهترین مسیر توسط مورچهها، ویژگیهای بسیار جالبی دارد، اول از همه قابلیت تعمیم زیاد و خود- سازمانده بودن آن است. در ضمن هیچ مکانیزم کنترل مرکزی ای وجود ندارد. ویژگی دوم قدرت زیاد آن است. سیستم شامل تعداد زیادی از عواملی است که به تنهایی بیاهمیت هستند بنابراین حتی تلفات یک عامل مهم، تأثیر زیادی روی کارایی سیستم ندارد. سومین ویژگی این است که، پروسه یک فرایند تطبیقی است. از آنجا که رفتار هیچکدام از مورچهها معین نیست و تعدادی از مورچهها همچنان مسیر طولانیتر را انتخاب میکنند، سیستم میتواند خود را با تغییرات محیط منطبق کند و ویژگی آخر اینکه این پروسه قابل توسعه است و میتواند به اندازهٔ دلخواه بزرگ شود. همین ویژگیها الهام بخش طراحی الگوریتمهایی شدهاند که در مسائلی که نیازمند این ویژگیها هستند کاربرد دارند. اولین الگوریتمی که بر این اساس معرفی شد، الگوریتم ABC بود. چند نمونه دیگر از این الگوریتمها عبارتند از: AntNet,ARA,PERA,AntHocNet.
انواع مختلف الگوریتم بهینهسازی مورچگان
در پایین تعدادی از انواع شناخته شده از الگوریتم بهینهسازی مورچگان را معرفی میکنیم:
۱- سیستم مورچه نخبگان: در این روش بهترین راه حل کلی در هر تکرار فرمون آزاد میکند. همچنین این روش برای تمام مورچههای مصنوعی باید انجام شود.
۲- سیستم مورچه ماکسیموم – مینیمم: یک مقدار کمینه و بیشینه برای فرمون تعیین کرده و فقط در هر مرحله بهترین جواب این مقدار را آزاد میکند و تمام گرههای مجاور ان به مقدار فرمون بیشینهمقدار دهی اولیه میشوند.
۳- سیستم کلونی مورچه: که در بالا توضیحات کافی داده شده است.
۴- سیستم مورچه بر اساس رتبه: تمام راه حلهای بدست آماده بر اساس طول جواب رتبهبندی میشوند و بر اساس همین رتبهبندی مقدار فرمون آزاد سازی شده توسط آنها مشخص خواهد شد و راه حل با طول کمتر از راه حل دیگر با طول بیشتر مقدار فرمون بیشتری آزاد میکند.
۵ – سیستم مورچه متعامد مداوم: در این روش مکانیزم تولید فرمون به مورچه اجازه میدهد تا برای رسیدن به جواب بهتر و مشترک با بقیه مورچهها جستجو انجام دهد با استفاده از روش طراحی متعامد مورچه میتواند در دامنه تعریف شده خود به صورت مداوم برای بدست آوردن بهترین جواب جستجو کند که این عمل به هدف رسیدن به جواب بهینه و صحیح ما را نزدیک میکند. روش طراحی متعامد میتواند به دیگر روشهای جستجو دیگر گسترش پیدا کنند تا به مزیتهای این روشهای جستجو اضافه کند.
منبع
انسان هميشه براي الهام گرفتن به جهان زنده پيرامون خود نگريسته است. يکي از بهترين طرح هاي شناخته شده، طرح پرواز انسان است که ابتدا لئورناردو داوينچي(1519-1452) طرحي از يک ماشين پرنده را بر اساس ساختمان بدن خفاش رسم نمود. چهار صد سال بعد کلمان آدر ماشين پرنده اي ساخت که داراي موتور بود و بجاي بال از ملخ استفاده مي کرد.
هم اکنون کار روي توسعه سيستم هاي هوشمند با الهام از طبيعت از زمينه هاي خيلي پرطرفدار هوش مصنوعي است. الگوريتمهاي ژنتيک که با استفاده از ايده تکاملي دارويني و انتخاب طبيعي مطرح شده، روش بسيار خوبي براي يافتن مسائل بهينه سازيست. ايده تکاملي دارويني بيانگر اين مطلب است که هر نسل نسبت به نسل قبل داراي تکامل است و آنچه در طبيعت رخ مي دهد حاصل ميليون ها سال تکامل نسل به نسل موجوداتي مثل مورچه است.
الگوريتم کلونی مورچه براي اولين بار توسط دوريگو (Dorigo) و همکارانش به عنوان يک راه حل چند عامله (Multi Agent) براي مسائل مشکل بهينه سازي مثل فروشنده دوره گرد (TSP :Traveling Sales Person) ارائه شد.
عامل هوشند(Intelligent Agent) موجودي است که از طريق حسگر ها قادر به درک پيرامون خود بوده و از طريق تاثير گذارنده ها مي تواند روي محيط تاثير بگذارد.
الگوريتم کلونی مورچه الهام گرفته شده از مطالعات و مشاهدات روي کلونی مورچه هاست. اين مطالعات نشان داده که مورچه ها حشراتي اجتماعي هستند که در کلونی ها زندگي مي کنند و رفتار آنها بيشتر در جهت بقاء کلونی است تا درجهت بقاء يک جزء از آن. يکي از مهمترين و جالبترين رفتار مورچه ها، رفتار آنها براي يافتن غذا است و بويژه چگونگي پيدا کردن کوتاهترين مسير ميان منابع غذايي و آشيانه. اين نوع رفتار مورچه ها داراي نوعي هوشمندي توده اي است که اخيرا مورد توجه دانشمندان قرار گرفته است.بايد تفاوت هوشمندي توده اي(کلونی) و هوشمندي اجتماعي را روشن کنيم.
در هوشمندي اجتماعي عناصر ميزاني از هوشمندي را دارا هستند. بعنوان مثال در فرآيند ساخت ساختمان توسط انسان، زماني که به يک کارگر گفته ميشود تا يک توده آجر را جابجا کند، آنقدر هوشمند هست تا بداند براي اينکار بايد از فرغون استفاده کند نه مثلا بيل!!! نکته ديگر تفاوت سطح هوشمندي افراد اين جامعه است. مثلا هوشمندي لازم براي فرد معمار با يک کارگر ساده متفاوت است.
در هوشمندي توده اي عناصر رفتاري تصادفي دارند و بين آن ها هيچ نوع ارتباط مستقيمي وجود ندارد و آنها تنها بصورت غير مستقيم و با استفاده از نشانه ها با يکديگر در تماس هستند. مثالي در اين مورد رفتار موريانه ها در لانه سازيست.
جهت علاقه مند شدن شما به اين رفتار موريانه ها وتفاوت هوشمندي توده اي و اجتماعي توضيحاتي را ارائه مي دهم :
فرآيند ساخت لانه توسط موريانه ها مورد توجه دانشمندي فرانسوي به نام گرس قرار گرفت. موريانه ها براي ساخت لانه سه فعاليت مشخص از خود بروز مي دهند. در ابتدا صدها موريانه به صورت تصادفي به اين طرف و آن طرف حرکت مي کنند. هر موريانه به محض رسيدن به فضايي که کمي بالاتر از سطح زمين قرار دارد شروع به ترشح بزاق مي کنند و خاک را به بزاق خود آغشته مي کنند. به اين ترتيب گلوله هاي کوچک خاکي با بزاق خود درست مي کنند. عليرغم خصلت کاملا تصادفي اين رفتار، نتيجه تا حدي منظم است.
در پايان اين مرحله در منطقه اي محدود تپه هاي بسيار کوچک مينياتوري از اين گلوله هاي خاکي آغشته به بزاق شکل مي گيرد. پس از اين، همه تپه هاي مينياتوري باعث مي شوند تا موريانه ها رفتار ديگري از خود بروز دهند. در واقع اين تپه ها به صورت نوعي نشانه براي موريانه ها عمل مي کنند. هر موريانه به محض رسيدن به اين تپه ها با انرژي بسيار بالايي شروع به توليد گلوله هاي خاکي با بزاق خود مي کند. اين کار باعث تبديل شدن تپه هاي مينياتوري به نوعي ستون مي شود. اين رفتار ادامه مي يابد تا زماني که ارتفاع هر ستون به حد معيني برسد. در اين صورت موريانه ها رفتار سومي از خود نشان مي دهند. اگر در نزديکي ستون فعلي ستون ديگيري نباشد بلافاصله آن ستون را رها مي کنند در غير اين صورت يعني در حالتي که در نزديکي اين ستون تعداد قابل ملاحظه اي ستون ديگر باشد، موريانه ها شروع به وصل کردن ستونها و ساختن لانه مي کنند.
تفاوتهاي هوشمندي اجتماعي انسان با هوشمندي توده اي موريانه را در همين رفتار ساخت لانه مي توان مشاهده کرد. کارگران ساختماني کاملا بر اساس يک طرح از پيش تعيين شده عمل مي کنند، در حالي که رفتار اوليه موريانه ها کاملا تصادفي است. علاوه بر اين ارتياط مابين کارگران سختماني مستقيم و از طريق کلمات و … است ولي بين موريانه ها هيچ نوع ارتباط مستقيمي وجود ندارد و آنها تنها بصورت غير مستقيم و از طريق نشانه ها با يکديگر در تماس اند. گرس نام اين رفتار را Stigmergie گذاشت، به معني رفتاري که هماهنگي مابين موجودات را تنها از طريق تغييرات ايجاد شده در محيط ممکن مي سازد.
بهينه سازي مسائل به روش کلونی مورچه ها (ACO) :
همانطور که مي دانيم مسئله يافتن کوتاهترين مسير، يک مسئله بهينه سازيست که گاه حل آن بسيار دشوار است و گاه نيز بسيار زمانبر. بعنوان مثال مسئله فروشنده دوره گرد(TSP). در اين مسئله فروشنده دوره گرد بايد از يک شهر شروع کرده، به شهرهاي ديگر برود و سپس به شهر مبدا بازگردد بطوريکه از هر شهر فقط يکبار عبور کند و کوتاهترين مسير را نيز طي کرده باشد. اگر تعداد اين شهرها n باشد در حالت کلي اين مسئله از مرتبه (n-1)! است که براي فقط 21 شهر زمان واقعا زيادي مي برد:
روز1013*7/1 = S1016*433/2 = ms10*1018*433/2 = !20
با انجام يک الگوريتم برنامه سازي پويا براي اين مسئله ، زمان از مرتبه نمايي بدست مي آيد که آن هم مناسب نيست. البته الگوريتم هاي ديگري نيز ارائه شده ولي هيچ کدام کارايي مناسبي ندارند. ACO الگوريتم کامل و مناسبي براي حل مسئله TSP است.
مورچه ها چگونه مي توانند کوتاهترين مسير را پيدا کنند؟
مورچه ها هنگام راه رفتن از خود ردي از ماده شيميايي فرومون(Pheromone) بجاي مي گذارند البته اين ماده بزودي تبخير مي شد ولي در کوتاه مدت بعنوان رد مورچه بر سطح زمين باقي مي ماند. يک رفتار پايه اي ساده در مورچه هاي وجود دارد :
آنها هنگام انتخاب بين دو مسير بصورت احتمالاتي( Statistical) مسيري را انتخاب مي کنند که فرومون بيشتري داشته باشد يا بعبارت ديگر مورچه هاي بيشتري قبلا از آن عبور کرده باشند. حال دقت کنيد که همين يک تمهيد ساده چگونه منجر به پيدا کردن کوتاهترين مسير خواهد شد :
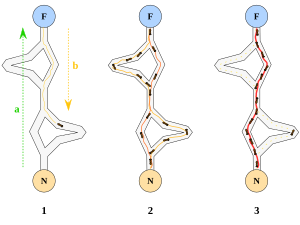
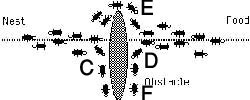
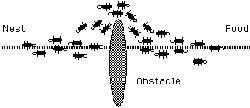
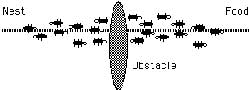
همانطور که در شکل 1-1 مي بينيم مورچه هاي روي مسير AB در حرکت اند (در دو جهت مخالف) اگر در مسير مورچه ها مانعي قرار ديهم(شکل 2-1) مورچه ها دو راه براي انتخاب کردن دارند. اولين مورچه ازA مي آيد و بهC مي رسد، در مسير هيچ فروموني نمي بيند بنابر اين براي مسير چپ و راست احتمال يکسان مي دهد و بطور تصادفي و احتمالاتي مسير CED را انتخاب مي کند. اولين مورچه اي که مورچه اول را دنبال مي کند زودتر از مورچه اولي که از مسير CFD رفته به مقصد مي رسد. مورچه ها در حال برگشت و به مرور زمان يک اثر بيشتر فرومون را روي CED حس مي کنند و آنرا بطور احتمالي و تصادفي ( نه حتما و قطعا) انتخاب مي کنند. در نهايت مسير CED بعنوان مسير کوتاهتر برگزيده مي شود. در حقيقت چون طول مسير CED کوتاهتر است زمان رفت و برگشت از آن هم کمتر مي شود و در نتيجه مورچه هاي بيشتري نسبت به مسير ديگر آنرا طي خواهند کرد چون فرومون بيشتري در آن وجود دارد.
نکه بسيار با اهميت اين است که هر چند احتمال انتخاب مسير پر فرومون ت توسط مورچه ها بيشتر است ولي اين کماکان احتمال است و قطعيت نيست. يعني اگر مسير CED پرفرومون تر از CFD باشد به هيچ عنوان نمي شود نتيجه گرفت که همه مورچه ها از مسيرCED عبور خواهند کرد بلکه تنها مي توان گفت که مثلا 90% مورچه ها از مسير کوتاهتر عبور خواهند کرد. اگر فرض کنيم که بجاي اين احتمال قطعيت وجود مي داشت، يعني هر مورچه فقط و فقط مسير پرفرومون تر را انتخاب ميکرد آنگاه اساسا اين روش ممکن نبود به جواب برسد. اگر تصادفا اولين مورچه مسيرCFD(مسير دورتر) را انتخاب مي کرد و ردي از فرومون بر جاي مي گذاشت آنگاه همه مورچه ها بدنبال او حرکت مي کردند و هيچ وقت کوتاهترين مسير يافته نمي شد. بنابراين تصادف و احتمال نقش عمده اي در ACO بر عهده دارند.
نکته ديگر مسئله تبخير شدن فرومون بر جاي گذاشته شده است. برفرض اگر مانع در مسير AB برداشته شود و فرومون تبخير نشود مورچه ها همان مسير قبلي را طي خواهند کرد. ولي در حقيقت اين طور نيست. تبخير شدن فرومون و احتمال به مورچه ها امکان پيدا کردن مسير کوتاهتر جديد را مي دهند.
1-1
2-1
3-1
4-1

مزيت هاي ACO :
همانطور که گقته شد «تبخير شدن فرومون» و «احتمال-تصادف» به مورچه ها امکان پيدا کردن کوتاهترين مسير را مي دهند. اين دو ويژگي باعث ايجاد انعطاف در حل هرگونه مسئله بهينه سازي مي شوند. مثلا در گراف شهرهاي مسئله فروشنده دوره گرد، اگر يکي از يالها (يا گره ها) حذف شود الگوريتم اين توانايي را دارد تا به سرعت مسير بهينه را با توجه به شرايط جديد پيدا کند. به اين ترتيب که اگر يال (يا گره اي) حذف شود ديگر لازم نيست که الگوريتم از ابتدا مسئله را حل کند بلکه از جايي که مسئله حل شده تا محل حذف يال (يا گره) هنوز بهترين مسير را داريم، از اين به بعد مورچه ها مي توانند پس از مدت کوتاهي مسير بهينه(کوتاهترين) را بيابند.
کاربردهاي ACO :
از کاربردهاي ACO مي توان به بهينه کردن هر مسئله اي که نياز به يافتن کوتاهترين مسير دارد ، اشاره نمود :
1. مسير يابي داخل شهري و بين شهري
2. مسير يابي بين پست هاي شبکه هاي توزيع برق ولتاژ بالا
3. مسير يابي شبکه هاي کامپيوتري
مسير يابي شبکه هاي کامپيوتري با استفاده از ACO :
اطلاعات بر روي شبکه بصورت بسته هاي اطلاعاتي کوچکي (Packet) منتقل مي شوند. هر يک از اين بسته ها بر روي شبکه در طي مسير از مبدا تا مقصد بايد از گره هاي زيادي که مسيرياب (Router) نام دارند عبور مي کنند. در داخل هر مسيرياب جدولي قرار دارد تا بهترين و کوتاهترين مسير بعدي تا مقصد از طريق آن مشخص مي شود، بنابر اين بسته هاي اطلاعاتي حين گذر از مسيرياب ها با توجه به محتويات اين جداول عبور داده مي شوند.
روشي بنام ACR : Ant Colony Routering پيشنهاد شده که بر اساس ايده کلونی مورچه به بهينه سازي جداول مي پردازيد و در واقع به هر مسيري با توجه به بهينگي آن امتياز مي دهد. استفاده از ACR به اين منظور داراي برتري نسبت به ساير روش هاست که با طبيعت ديناميک شبکه سازگاري دارد، زيرا به عنوان مثال ممکن است مسيري پر ترافيک شود يا حتي مسير يابي (Router) از کار افتاده باشد و بدليل انعطاف پذيري که ACO در برابر اين تغييرات دارد همواره بهترين راه حل بعدي را در دسترس قرار مي دهد.
الگوریتم کلونی مورچه ها قسمت 1
الگوریتم کلونی مورچه ها قسمت 2
الگوریتم کلونی مورچه ها قسمت 3

















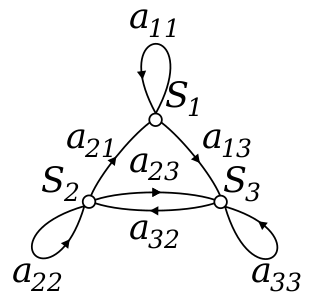
![{\displaystyle \ A=[a_{ij}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c2e5be58535cfa69a95badb38fd3533bfb6235e)






































![{\displaystyle H_{ij}=E[T_{ij}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7534400c9445d555950b49a2d86f7bcf4389ee29)

















![{\displaystyle p_{ij}^{(n)}=[P^{n}]_{ij}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd3b38dcfe4aa747f5765dbfa1368ae661c7fb65)












![{\displaystyle M_{i}=E[T_{i}]=\sum _{n=1}^{\infty }n\cdot f_{ii}^{(n)}.\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e7182ea52ad054b13097e3b47c7f38fa22bdca87)

























.jpg)