بایگانی برچسب برای: v’vsdk

ماشین بردار پشتیبان (svm) قسمت 3

تاريخچه

الگوريتم SVM اوليه در ۱۹۶۳ توسط Vladimir Vapnik ابداع شد و در سال ۱۹۹۵ توسطVapnik و Corinna Cortes براي حالت غيرخطي تعميم داده شد.

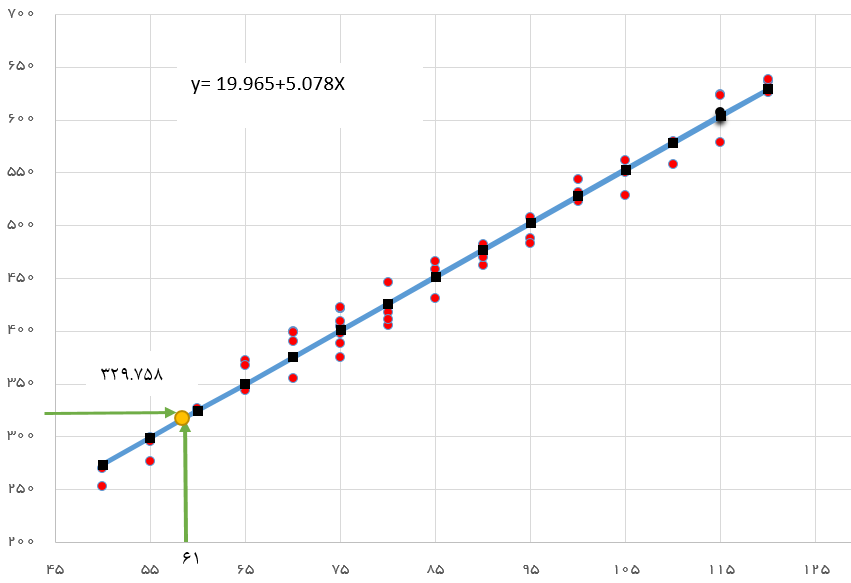
ماشين بردار پشتيباني (Support vector machines) يکي از روش‌هاي يادگيري بانظارت(Supervised learning) است که از آن براي طبقه‌بندي و رگرسيون استفاده مي‌کنند.

اين روش از جمله روش‌هاي نسبتاً جديدي است که در سال‌هاي اخير کارايي خوبي نسبت به روش‌هاي قديمي‌تر براي طبقه‌بندي از جمله شبکه‌هاي عصبي پرسپترون نشان داده است. مبناي کاري دسته‌بنديکنندة SVM دسته‌بندي خطي داده‌ها است و در تقسيم خطي داده‌ها سعي مي‌کنيم خطي را انتخاب کنيم که حاشيه اطمينان بيشتري داشته باشد. حل معادلة پيدا کردن خط بهينه براي داده‌ها به وسيله روش‌هايQP (Quadratic Programming) که روش‌هاي شناخته شده‌اي در حل مسائل محدوديت‌دار هستند صورت مي‌گيرد.

SVM از يک تکنيک که kernel trick ناميده مي شود، براي تبديل داده هاي شما استفاده مي کند و سپس بر اساس اين تبديل، مرز بهينه بين خروجي هاي ممکن را پيدا مي کند. به عبارت ساده تبديلات بسيار پيچيده را انجام مي دهد، سپس مشخص مي کند چگونه داده هايتان را بر اساس برچسب ها يا خروجي هايي که تعريف کرده ايد، جدا کنيد.

يکي از روش هايي که در حال حاضر به صورت گسترده براي مسئله دسته بندي (Classification) مورد استفاده قرار مي گيرد، روش ماشين بردار پشتيبان (SVM) است. شايد به گونه اي بتوان محبوبيت کنوني روش ماشين بردار پشتيبان را با محبوبيت شبکه هاي عصبي در دهه گذشته مقايسه کرد. علت اين قضيه نيز قابليت استفاده اين روش در حل مسائل گوناگون مي باشد، در حاليکه روش هايي مانند درخت تصميم گيري را نمي توان به راحتي در مسائل مختلف به کار برد.

کاربردهاي SVM

الگوريتم  SVM، جز الگوريتم هاي تشخيص الگو دسته بندي مي شود. از الگوريتم SVM، در هر جايي که نياز به تشخيص الگو يا دسته بندي اشيا در کلاس هاي خاص باشد مي توان استفاده کرد. در ادامه به کاربرد هاي اين الگوريتم به صورت موردي اشاره مي شود:

سيستم آناليز ريسک، کنترل هواپيما بدون خلبان، رديابي انحراف هواپيما، شبيه سازي مسير، سيستم راهنمايي اتوماتيک اتومبيل، سيستمهاي بازرسي کيفيت، آناليز کيفيت جوشکاري، پيش بيني کيفيت، آناليز کيفيت کامپيوتر، آناليز عملياتهاي آسياب، آناليز طراحي محصول شيميايي، آناليز نگهداري ماشين، پيشنهاد پروژه، مديريت و برنامه ريزي، کنترل سيستم فرايند شيميايي و ديناميکي، طراحي اعضاي مصنوعي، بهينه سازي زمان پيوند اعضا، کاهش هزينه بيمارستان، بهبود کيفيت بيمارستان، آزمايش اتاق اورژانس، اکتشاف روغن و گاز، کنترل مسير در دستگاههاي خودکار، ربات، جراثقال، سيستمهاي بصري، تشخيص صدا، اختصار سخن، کلاسه بندي صوتي، آناليز بازار، سيستمهاي مشاوره اي محاسبه هزينه موجودي، اختصار اطلاعات و تصاوير، خدمات اطلاعاتي اتوماتيک، مترجم لحظه اي زبان، سيستمهاي پردازش وجه مشتري، سيستمهاي تشخيص ترمز کاميون، زمانبندي وسيله نقليه، سيستمهاي مسيريابي، کلاسه بندي نمودارهاي مشتري/بازار، تشخيص دارو، بازبيني امضا، تخمين ريسک وام، شناسايي طيفي، ارزيابي سرمايه، کلاسه بندي انواع سلولها، ميکروبها و نمونه ها، پيش بيني فروشهاي آينده، پيش بيني نيازهاي محصول، پيش بيني وضعيت بازار، پيش بيني شاخصهاي اقتصادي، پيش بيني ملزومات انرژي، پيش بيني واکنشهاي دارويي، پيش بيني بازتاب محصولات شيميايي، پيش بيني هوا، پيش بيني محصول، پيش بيني ريسک محيطي، پيش بيني جداول داوري، مدل کردن کنترل فرآيند، آناليز فعاليت گارانتي، بازرسي اسناد، تشخيص هدف، تشخيص چهره، انواع جديد سنسورها، دستگاه کاشف زير دريايي بوسيله امواج صوتي، رادار، پردازش سيگنالهاي تصويري شامل مقايسه اطلاعات، پيگيري هدف، هدايت جنگ افزارها، تعيين قيمت وضعيت فعلي، جلوگيري از پارازيت، شناسايي تصوير /سيگنال، چيدمان يک مدار کامل، بينايي ماشين، مدل کردن غير خطي، ترکيب صدا، کنترل فرآيند ساخت، آناليز مالي، پيش بيني فرآيندهاي توليد، ارزيابي بکارگيري يک سياست، بهينه سازي محصول، تشخيص ماشين و فرآيند، مدل کردن کنترل سيستمها، مدل کردن ساختارهاي شيميايي، مدل کردن سيستمهاي ديناميکي، مدل کردن سيگنال تراکم، مدل کردن قالبسازي پلاستيکي، مديريت قراردادهاي سهام، مديريت وجوه بيمه، ديريت سهام، تصويب چک بانکي، اکتشاف تقلب در کارت اعتباري، ثبت نسيه، بازبيني امضا از چکها، پيش بيني ارزش نسيه، مديريت ريسک رهن، تشخيص حروف و اعدا، تشخيص بيماري و…..

ايده اصلي SVM

l      با فرض اينکه دسته ها بصورت خطي جداپذير باشند، ابرصفحه هائي با حداکثر حاشيه(maximum margin)  را بدست مي آورد که دسته ها را جدا کنند.

l      در مسايلي که داده ها بصورت خطي جداپذير نباشند، داده ها به فضاي با ابعاد بيشتر نگاشت پيدا مي کنند تا بتوان آنها را در اين فضاي جديد بصورت خطي جدا نمود.

l      در يک فرايند يادگيري که شامل دو کلاس مي­باشد، هدف SVM پيدا کردن بهترين تابع براي طبقه­بندي مي­باشد به نحوي که بتوان اعضاي دو کلاس را در مجموعه داده­ها از هم تشخيص داد. معيار بهترين طبقه­بندي به­صورت هندسي مشخص مي­شود، براي مجموعه داده­هايي که به­صورت خطي قابل تجزيه هستند. به­طور حسي آن مرزي که به­صورت بخشي از فضا تعريف مي­شود يا همان تفکيک بين دو کلاس بوسيله hyperplane تعريف مي­شود. همين تعريف هندسي به ما اجازه مي­دهد تا کشف کنيم که چگونه مرزها را بيشينه کنيم ولو اينکه تعداد بيشماري hyperplane داشته باشيم و فقط تعداد کمي، شايستگي راه حل براي SVM دارند.

مسئله جداسازي خطي: Linear Discrimination

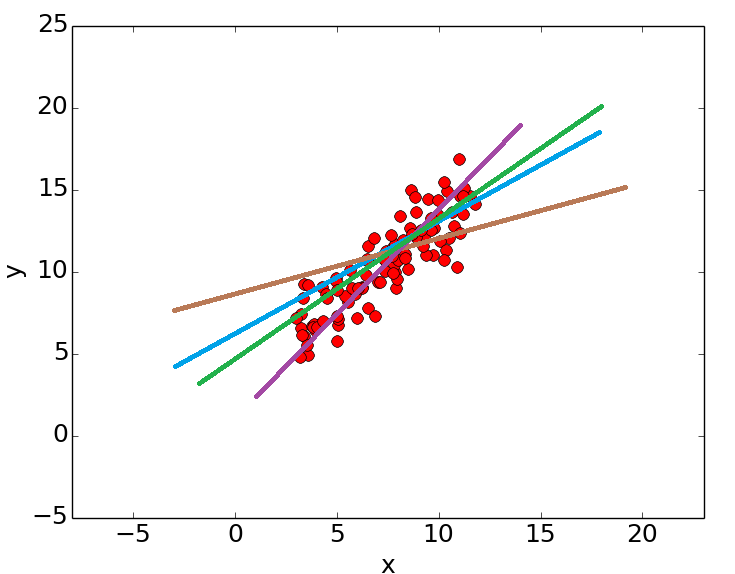
اگر دو دسته وجود داشته باشند که بصورت خطي از هم جداپذير باشند، بهترين جدا کننده اين دو دسته چيست؟

الگوريتم هاي مختلفي از جمله  پرسپترون ميتوانند اين جداسازي را انجام دهند.

آيا همه اين الگوريتمها بخوبي از عهده اين کار بر مي آيند؟

 

آشنايي با مفاهيم ابتدايي

خط يا ابر صفحه جدا کننده:

هدف: پيدا کردن بهترين خط ( ابر صفحه) که دو دسته را از هم جدا کند. در حالت دو بعدي معادله اين خط بصورت زير است:

در حالت n  بعدي خواهيم داشت:

حداکثر حاشيه (maximum margin)

بر طبق قضيه اي در تئوري يادگيري اگر مثالهاي آموزشي بدرستي دسته بندي شده باشند، از بين جداسازهاي خطي، آن جداسازي که حاشيه داده هاي آموزشي را حداکثر مي کند، خطاي تعميم را حداقل خواهد کرد.

چرا حداکثر حاشيه؟

¢     به نظر مي رسد که مطمئن ترين راه باشد.

¢     تئوري هائي برمبناي VC dimension وجود دارد که مفيد بودن آنرا اثبات مي کند.

¢     بطور تجربي اين روش خيلي خوب جواب داده است.

¢     دليل اينکه SVM روي بزرگ­ترين مرز براي hyperplane پافشاري مي­کند اين­ست که قضيه قابليت عموميت بخشيدن به الگوريتم را بهتر تامين مي­کند. اين نه تنها به کارايي طبقه­بندي و دقت  آن روي داده­هاي آزمايشي کمک مي­کند، فضا را نيز براي طبقه­بندي بهتر داده­هاي آتي مهيا مي­کند.

بردار پشتيبان

نزديکترين داده هاي آموزشي به ابر صفحه هاي جدا کننده بردار پشتيبان ناميده مي شوند.

ماشين بردار پشتيبان خطي

ماشين بردار پشتيبان يک روش يادگيري نسبتا جديد است که اغلب براي کلاسبندي باينري مورد استفاده واقع مي شود. فرض کنيد L مشاهده داريم که هر مشاهده مشتمل بر زوج هاي است که در آن . بردار ورودي و  يک مقدار دو وضعيتي (1- يا 1+) است. ايده ي ماشين بردار پشتيبان مي کوشد، ابرصفحاتي در فضا رسم کند که عمل تمايز نمونه هاي کلاس هاي مختلف داده ها را بطور بهينه انجام دهد. مي توان يک ابرصفحه را از طريق رابطه زير نشان داد:

براي يک بردار خطي b با وزن w ، حاشيه جداسازي عبارتست از فاصله ي بين ابرصفحه تعريف شده توسط رابطه ي فوق و نزديکترين ويژگي به آن. هدف ماشين بردار پشتيبان يافتن ابرصفحه اي ست که بيشترين حاشيه ي جداسازي را داشته باشد. مهمترين وظيفه SVM ، يافتن پارامترهاي w0 و b0 بر اساس بردارهاي آموزشي داده شده، براي اين ابرصفحه بهينه است. براي يک بردار ويژگي X، فاصله تا ابرصفحه بهينه به صورت زير است:

از رابطه بالا نتيجه مي شود که ماکزيموم کردن حاشيه جداسازي بين الگوها و ابرصفحه، معادلست با مينيموم کردن فرم اقليدسي بردار وزن w. بنابراين مساله بهينه سازي مقيد را مي توان به صورت زير تعريف کرد:

براي حل اين مساله، تابع لاگرانژ زير را تشکيل داده و حل مي کنيم:

لاگرانژين L بايد نسبت به متغيرهاي اوليه  bو w مينيموم و نسبت به متغيرهاي دوگان ماکزيموم شود. با مساوي صفر قراردادن مشتق L نسبت به b،w:

به معادلات زير خواهيم رسيد:

مجموعه جواب، بسطي از نمونه هاي آموزشي است که مقدار  متناظر با آن ها، يک مقدار غير صفر است. اين نمونه هاي آموزشي خاص به بردارهاي پشتيبان مشهورند. بردارهاي پشتيبان روي مرز حاشيه قرار دارند. مابقي نمونه هاي آموزشي در اين قسمت نقشي ندارند.

تمايز نمونه هاي دو کلاس با ابرصفحه ي بهينه

با قرار دادن 7 و 8 در  به مساله دوگان ولف زير خواهيم رسيد:

حل اين مساله دوگان ضرايب لاگرانژ را به ما مي دهد. تابع ابرصفحه متمايز کننده را مي توان به صورت زير نوشت:

ماشين بردار پشتيبان براي بردارهاي ورودي جدايي ناپذير:

اغلب در عمل، يافتن يک ابرصفحه متمايز کننده به راحتي امکان پذير نيست. زيرا مثلا يک نويز قوي مي تواند باعث ايجاد رويهم افتادگي کلاس ها شود. در اين حالت از متغير هايي به نام متغيرهاي کمبود(Slack Variables) استفاده مي کنيم. به گونه اي که شرايط زير برقرار باشند:

حال يک تعميم خوب براي ابرصفحه ي متمايز کننده، با کنترل ظرفيت کلاسبند (از طريق ) و همچنين تعداد خطاهاي مرحله آموزش بدست مي آيد. مساله بهينه سازي به صورت زير تعريف خواهد شد:

مساله دوگان به فرم زير خواهد بود:

ماشين بردار پشتيبان غيرخطي:

ابرصفحه جداکننده بهينه اولين بار توسط Vapnik در سال ۱۹۶۳ ارائه شد که يک دسته کننده خطي بود. در سال ۱۹۹۲ ،Bernhard Boser ،  Isabelle GuyonوVapnik راهي را براي ايجاد دسته بند غيرخطي، با استفاده قرار دادن هسته براي پيدا کردن ابرصفحه با بيشتر حاشيه، پيشنهاد دادند. الگوريتم نتيجه شده ظاهرا مشابه است، به جز آنکه تمام ضرب هاي نقطه اي با يک تابع هسته غيرخطي جايگزين شده اند. اين اجازه مي دهد، الگوريتم، براي ابرصفحه با بيشترين حاشيه در يک فضاي ويژگيِ تغييرشکل داده، مناسب باشد. ممکن است، تغييرشکل غيرخطي باشد و فضاي تغيير يافته، داراي ابعاد بالاتري باشد. به هر حال دسته کننده، يک ابرصفحه در فضاي ويژگي با ابعاد بالا است، که ممکن است در فضاي ورودي نيز غيرخطي باشد.

در حالت غيرخطي، مي توان با اعمال پيش پردازش داده ها، مساله را به فضايي برد که در آن جا با يک ابرصفحه ساده قابل حل باشد. براي اين منظور يک نگاشت  تعريف مي کنيم که بردار ورودي d بعدي x را به بردار d’ بعدي z تبديل مي کند.

بايد به گونه اي انتخاب شود که بردارهاي فضاي ويژگي جديد جدايي پذير باشند. در حالت کلي مي توان گفت که اگر  بردارهاي ورودي را به فضايي ببرد که تعداد ابعاد آن به اندازه کافي بزرگ باشد (

منبع

منابع

1.https://fa.wikipedia.org

2.http://www.bigdata.ir

3.www.barjoueian.com

4.http://fumblog.um.ac.ir

ماشین بردار پشتیبان (svm) قسمت 1
ماشین بردار پشتیبان (svm) قسمت 2
ماشین بردار پشتیبان (svm) قسمت 3

/0 دیدگاه /توسط

ماشین بردار پشتیبان (svm) قسمت 1

ماشین بردار پشتیبانی

ماشین بردار پشتیبان (Support vector machines – SVMs) یکی از روش‌های یادگیری بانظارت است که از آن برای طبقه‌بندی و رگرسیون استفاده می‌کنند.

این روش از جملهٔ روش‌های نسبتاً جدیدی است که در سال‌های اخیر کارایی خوبی نسبت به روش‌های قدیمی‌تر برای طبقه‌بندی از جمله شبکه‌های عصبی پرسپترون نشان داده است. مبنای کاریدسته‌بندی کنندۀ SVM دسته‌بندی خطی داده‌ها است و در تقسیم خطی داده‌ها سعی می‌کنیم خطی را انتخاب کنیم که حاشیه اطمینان بیشتری داشته باشد. حل معادله پیدا کردن خط بهینه برای داده‌ها به وسیله روش‌های QP که روش‌های شناخته شده‌ای در حل مسائل محدودیت‌دار هستند صورت می‌گیرد. قبل از تقسیمِ خطی برای اینکه ماشین بتواند داده‌های با پیچیدگی بالا را دسته‌بندی کند داده‌ها را به وسیلهٔ تابعِ phi به فضای با ابعاد خیلی بالاتر می‌بریم. برای اینکه بتوانیم مسئله ابعاد خیلی بالا را با استفاده از این روش‌ها حل کنیم از قضیه دوگانی لاگرانژ برای تبدیلِ مسئلهٔ مینیمم‌سازی مورد نظر به فرم دوگانی آن که در آن به جای تابع پیچیدهٔ phi که ما را به فضایی با ابعاد بالا می‌برد، تابعِ ساده‌تری به نامِ تابع هسته که ضرب برداری تابع phi است ظاهر می‌شود استفاده می‌کنیم. از توابع هسته مختلفی از جمله هسته‌های نمایی، چندجمله‌ای و سیگموید می‌توان استفاده نمود.

یکی از معروفترین خودآموزها مربوط به است.

کاربردهای SVM

الگوریتم SVM، جز الگوریتم‌های تشخیص الگو دسته بندی می‌شود.از الگوریتم SVM، در هر جایی که نیاز به تشخیص الگو یا دسته بندی اشیا در کلاس‌های خاص باشد می‌توان استفاده کرد.در ادامه به کاربردهای این الگوریتم به صورت موردی اشاره می‌شود:

سیستم آنالیز ریسک، کنترل هواپیما بدون خلبان، ردیابی انحراف هواپیما، شبیه‌سازی مسیر، سیستم راهنمایی اتوماتیک اتومبیل، سیستم‌های بازرسی کیفیت، آنالیز کیفیت جوشکاری، پیش‌بینی کیفیت، آنالیز کیفیت کامپیوتر، آنالیز عملیاتهای آسیاب، آنالیز طراحی محصول شیمیایی، آنالیز نگهداری ماشین، پیشنهاد پروژه، مدیریت و برنامه‌ریزی، کنترل سیستم فرایند شیمیایی و دینامیکی، طراحی اعضای مصنوعی، بهینه‌سازی زمان پیوند اعضا، کاهش هزینه بیمارستان، بهبود کیفیت بیمارستان، آزمایش اتاق اورژانس، اکتشاف روغن و گاز، کنترل مسیر در دستگاه‌های خودکار، ربات، جراثقال، سیستم‌های بصری، تشخیص صدا، اختصار سخن، کلاسه بندی صوتی، آنالیز بازار، سیستم‌های مشاوره‌ای محاسبه هزینه موجودی، اختصار اطلاعات و تصاویر، خدمات اطلاعاتی اتوماتیک، مترجم لحظه‌ای زبان، سیستم‌های پردازش وجه مشتری، سیستم‌های تشخیص ترمز کامیون، زمانبندی وسیله نقلیه، سیستم‌های مسیریابی، کلاسه بندی نمودارهای مشتری/بازار، تشخیص دارو، بازبینی امضا، تخمین ریسک وام، شناسایی طیفی، ارزیابی سرمایه، کلاسه بندی انواع سلول‌ها، میکروبها و نمونه ها، پیش‌بینی فروشهای آینده، پیش‌بینی نیازهای محصول، پیش‌بینی وضعیت بازار، پیش‌بینی شاخصهای اقتصادی، پیش‌بینی ملزومات انرژی، پیش‌بینی واکنش‌های دارویی، پیش‌بینی بازتاب محصولات شیمیایی، پیش‌بینی هوا، پیش‌بینی محصول، پیش‌بینی ریسک محیطی، پیش‌بینی جداول داوری، مدل کردن کنترل فرایند، آنالیز فعالیت گارانتی، بازرسی اسناد، تشخیص هدف، تشخیص چهره، انواع جدید سنسورها، دستگاه کاشف زیر دریایی بوسیله امواج صوتی، رادار، پردازش سیگنالهای تصویری شامل مقایسه اطلاعات، پیگیری هدف، هدایت جنگ افزارها، تعیین قیمت وضعیت فعلی، جلوگیری از پارازیت، شناسایی تصویر /سیگنال، چیدمان یک مدار کامل، بینایی ماشین، مدل کردن غیر خطی، ترکیب صدا، کنترل فرایند ساخت، آنالیز مالی، پیش‌بینی فرایندهای تولید، ارزیابی بکارگیری یک سیاست، بهینه‌سازی محصول، تشخیص ماشین و فرایند، مدل کردن کنترل سیستم‌ها، مدل کردن ساختارهای شیمیایی، مدل کردن سیستم‌های دینامیکی، مدل کردن سیگنال تراکم، مدل کردن قالب‌سازی پلاستیکی، مدیریت قراردادهای سهام، مدیریت وجوه بیمه، دیریت سهام، تصویب چک بانکی، اکتشاف تقلب در کارت اعتباری، ثبت نسیه، بازبینی امضا از چکها، پیش‌بینی ارزش نسیه، مدیریت ریسک رهن، تشخیص حروف و اعدا، تشخیص بیماری و…..

تاریخچه

الگوریتم SVM اولیه در ۱۹۶۳ توسط Vladimir Vapnik ابداع شدو در سال ۱۹۹۵ توسط Vapnik و Corinna Cortes برای حالت غیرخطی تعمیم داده شد.

خلاصه استفاده عملی از SVM

ماتریس الگو را آماده می کنیم. تابع کرنلی را برای استفاده انتخاب می کنیم. پارامتر تابع کرنل و مقدار C را انتخاب می کنیم. برای محاسبه ی مقادیرα_i الگوریتم آموزشی را با استفاده از حل‌کننده‌های QP اجرا می کنیم. داده‌های جدید با استفاده از مقادیرα_i و بردارهای پشتیبان می‌توانند دسته بندی شوند.

مزایا و معایب SVM

آموزش نسبتاً ساده است برخلاف شبکه‌های عصبی در ماکزیمم‌های محلی گیر نمی‌افتد. برای داده‌های با ابعاد بالا تقریباً خوب جواب می‌دهد. مصالحه بین پیچیدگی دسته بندی‌کننده و میزان خطا به‌طور واضح کنترل می‌شود. به یک تابع کرنل خوب و انتخاب پارامتر C نیاز دارد.

ماشین بردار پشتیبان خطی

شکل 1

ما مجموعه داده‌های آزمایش {\displaystyle {\mathcal {D}}} شامل n عضو(نقطه)را در اختیار داریم که به صورت زیر تعریف می‌شود:

{\displaystyle {\mathcal {D}}=\left\{(\mathbf {x} _{i},y_{i})\mid \mathbf {x} _{i}\in \mathbb {R} ^{p},\,y_{i}\in \{-1,1\}\right\}_{i=1}^{n}}

جایی که مقدار y برابر ۱ یا -۱ و هر {\displaystyle \mathbf {x} _{i}} یک بردار حقیقی p-بعدی است. هدف پیدا کردن ابرصفحه جداکننده با بیشترین فاصله از نقاط حاشیه‌ای است که نقاط با {\displaystyle y_{i}=1} را از نقاط با {\displaystyle y_{i}=-1} جدا کند. هر ابر صفحه می‌تواند به صورت مجموعه‌ای از نقاط {\mathbf {x}} که شرط زیر را ارضا می‌کند نوشت:

{\displaystyle \mathbf {w} \cdot \mathbf {x} -b=0,\,} جایی که . علامت ضرب است. {\displaystyle {\mathbf {w} }} بردار نرمال است، که به ابرصفحه عمود است. ما می خواهیم {\displaystyle {\mathbf {w} }} و {\displaystyle {\mathbf {b} }} را طوری انتخاب کنیم که بیشترین فاصله بین ابر صفحه‌های موازی که داده‌ها را از هم جدا می‌کنند، ایجاد شود. این ابرصفحه‌ها با استفاده از رابطه زیر توصیف می‌شوند.
{\displaystyle \mathbf {w} \cdot \mathbf {x} -b=1\,}

و

شکل 2
{\displaystyle \mathbf {w} \cdot \mathbf {x} -b=-1.\,}
اگر داده‌های آموزشی جدایی پذیر خطی باشند، ما می‌توانیم دو ابر صفحه در حاشیه نقاط به‌طوری‌که هیچ نقطه مشترکی نداشته باشند، در نظر بگیریم و سپس سعی کنیم، فاصله آن‌ها را، ماکسیمم کنیم. با استفاده از هندسه، فاصله این دو صفحه {\displaystyle {\tfrac {2}{\|\mathbf {w} \|}}} است. بنابراین ما باید {\displaystyle \|\mathbf {w} \|} را مینیمم کنیم. برای اینکه از ورود نقاط به حاشیه جلوگیری کنیم، شرایط زیر را اضافه می کنیم: برای هر i
of the first class {\displaystyle \mathbf {w} \cdot \mathbf {x} _{i}-b\geq 1\qquad {\text{ for }}\mathbf {x} _{i}}

یا

of the second class {\displaystyle \mathbf {w} \cdot \mathbf {x} _{i}-b\leq -1\qquad {\text{ for }}\mathbf {x} _{i}}

این می‌تواند به صورت زیر نوشته شود:

{\displaystyle y_{i}(\mathbf {w} \cdot \mathbf {x} _{i}-b)\geq 1,\quad {\text{ for all }}1\leq i\leq n.\qquad \qquad (1)}

با کنار هم قرار دادن این دو یک مسئله بهینه‌سازی به دست می‌آید:

Minimize (in {\displaystyle {\mathbf {w} ,b}})

{\displaystyle \|\mathbf {w} \|}

subject to (for any {\displaystyle i=1,\dots ,n})

{\displaystyle y_{i}(\mathbf {w} \cdot \mathbf {x_{i}} -b)\geq 1.\,}

فرم اولیه

مسئله بهینه‌سازی مشاهده شده در قسمت قبل، مسئله سختی، برای حل کردن است، زیرا به||w|| وابسته است (نرم w ) . خوشبختانه می‌توانیم، بدون تغییر در مسئله||w|| را با{\displaystyle {\tfrac {1}{2}}\|\mathbf {w} \|^{2}}جانشین کنیم( عبارت ½ برای آسودگی در محاسبات ریاضی آورده شده). این یک مسئله بهینه سازی (OP)برنامه‌ریزی غیرخطی(QP) است. به‌طور واضح تر :

Minimize (in {\displaystyle {\mathbf {w} ,b}}) c

{\displaystyle {\frac {1}{2}}\|\mathbf {w} \|^{2}}

subject to (for any {\displaystyle i=1,\dots ,n})

{\displaystyle y_{i}(\mathbf {w} \cdot \mathbf {x_{i}} -b)\geq 1.}

می توان عبارت قبل را با استفاده از ضرایب نا منفی لاگرانژ به صورت زیر نوشت که در آن ضرایب لاگرانژ هستند {\displaystyle \alpha _{i}}:

{\displaystyle \min _{\mathbf {w} ,b,{\boldsymbol {\alpha }}}\{{\frac {1}{2}}\|\mathbf {w} \|^{2}-\sum _{i=1}^{n}{\alpha _{i}[y_{i}(\mathbf {w} \cdot \mathbf {x_{i}} -b)-1]}\}}

اما فرمول فوق اشتباه است . فرض کنید ما بتوانیم خانواده‌ای از ابرصفحات که نقاط را تقسیم می‌کنند پیدا کنیم . پس همه {\displaystyle y_{i}(\mathbf {w} \cdot \mathbf {x_{i}} -b)-1\geq 0} . بنا بر این ما می‌توانیم مینیمم را با فرستادن همه {\displaystyle \alpha _{i}} به{\displaystyle +\infty } پیدا کنیم. با این حال شرط پیش گفته می‌تواند به صورت پایین بیان شود:

{\displaystyle \min _{\mathbf {w} ,b}\max _{\boldsymbol {\alpha }}\{{\frac {1}{2}}\|\mathbf {w} \|^{2}-\sum _{i=1}^{n}{\alpha _{i}[y_{i}(\mathbf {w} \cdot \mathbf {x_{i}} -b)-1]}\}}

ما به دنبال نقاط saddle میگردیم.حالا می‌توان این مسئله را به کمک برنامه‌ریزی غیرخطی استاندارد حل کرد. جواب می‌تواند به صورت ترکیب خطی از بردارهای آموزشی بیان شود :

{\displaystyle \mathbf {w} =\sum _{i=1}^{n}{\alpha _{i}y_{i}\mathbf {x_{i}} }}

تنها چند{\displaystyle \alpha _{i}} بزرگتر از صفر خواهد بود.{\displaystyle \mathbf {x_{i}} } متناظر، دقیقاً همان بردار پشتیبان خواهد بود و به شرط را ارضا خواهد کرد. از این می‌توان نتیجه گرفت که بردارهای پشتیبان شرط زیر را نیز ارضا می‌کنند: {\displaystyle y_{i}(\mathbf {w} \cdot \mathbf {x_{i}} -b)=1} که اجازه می دهد مفدار b تعریف شود. در عمل الگوریتم مقاوم تر خواهد بود اگر از تمام {\displaystyle N_{SV}} بردار پشتیبان میانگین گرفته شود:

{\displaystyle b={\frac {1}{N_{SV}}}\sum _{i=1}^{N_{SV}}{(\mathbf {w} \cdot \mathbf {x_{i}} -y_{i})}}

فرم دوگان

استفاده از این واقعیت که {\displaystyle \|\mathbf {w} \|^{2}=w\cdot w} و جانشینی {\displaystyle \mathbf {w} =\sum _{i=1}^{n}{\alpha _{i}y_{i}\mathbf {x_{i}} }} می‌توان نشان داد که دوگان SVM به مسئله بهینه‌سازی زیر ساده می‌شود:

Maximize (in {\displaystyle \alpha _{i}} )

{\displaystyle {\tilde {L}}(\mathbf {\alpha } )=\sum _{i=1}^{n}\alpha _{i}-{\frac {1}{2}}\sum _{i,j}\alpha _{i}\alpha _{j}y_{i}y_{j}\mathbf {x} _{i}^{T}\mathbf {x} _{j}=\sum _{i=1}^{n}\alpha _{i}-{\frac {1}{2}}\sum _{i,j}\alpha _{i}\alpha _{j}y_{i}y_{j}k(\mathbf {x} _{i},\mathbf {x} _{j})}

subject to (for any}{\displaystyle i=1,\dots ,n})

{\displaystyle \alpha _{i}\geq 0,\,}

and to the constraint from the minimization in {\displaystyle b}

{\displaystyle \sum _{i=1}^{n}\alpha _{i}y_{i}=0.}

در اینجا هسته به صورت {\displaystyle k(\mathbf {x} _{i},\mathbf {x} _{j})=\mathbf {x} _{i}\cdot \mathbf {x} _{j}} تعریف می‌شود. عبارت \alpha  تشکیل یک دوگان برای بردار وزن‌ها مجموعه آموزشی می دهد:

{\displaystyle \mathbf {w} =\sum _{i}\alpha _{i}y_{i}\mathbf {x} _{i}.}

ماشین بردار پشتیبان چند کلاسی

SVM اساساً یک جداکننده دودویی است. در بخش قبلی پایه‌های تئوری ماشین‌های بردار پشتیبان برای دسته بندی دو کلاس تشریح شد. یک تشخیص الگوی چند کلاسی می‌تواند به وسیله ی ترکیب ماشین‌های بردار پشیبان دو کلاسی حاصل شود. به‌طور معمول دو دید برای این هدف وجود دارد. یکی از آن‌ها استراتژی “یک در مقابل همه ” برای دسته بندی هر جفت کلاس و کلاس‌های باقی‌مانده‌است. دیگر استراتژی “یک در مقابل یک” برای دسته بندی هر جفت است. در شرایطی که دسته بندی اول به دسته بندی مبهم منجر می‌شود.برای مسائل چند کلاسی٬رهیافت کلی کاهش مسئله ی چند کلاسی به چندین مسئله دودویی است. هریک از مسائل با یک جداکننده دودویی حل می‌شود. سپس خروجی جداکننده‌های دودویی SVM با هم ترکیب شده و به این ترتیب مسئله چند کلاس حل می‌شود.

ماشین‌های بردار پشتیبان غیرخطی

شکل 3

ابرصفحه جداکننده بهینه اولین بار توسط Vapnik در سال ۱۹۶۳ ارائه شد که یک دسته‌کننده خطی بود. در سال ۱۹۹۲ ،Bernhard Boser ، Isabelle GuyonوVapnik راهی را برای ایجاد دسته بند غیرخطی، با استفاده قرار دادن هسته برای پیدا کردن ابرصفحه با بیشتر حاشیه، پیشنهاد دادند. الگوریتم نتیجه شده ظاهراً مشابه است، به جز آنکه تمام ضرب‌های نقطه‌ای با یک تابع هسته غیرخطی جایگزین شداند. این اجازه می‌دهد، الگوریتم، برای ابرصفحه با بیشترین حاشیه در یک فضای ویژگی تغییرشکل داده، مناسب باشد. ممکن است، تغییرشکل غیرخطی باشد و فضای تغییر یافته، دارای ابعاد بالاتری باشد. به هر حال دسته‌کننده، یک ابرصفحه در فضای ویژگی با ابعاد بالا است، که ممکن است در فضای ورودی نیز غیرخطی باشد.

اگر از هسته با تابع گوسیین استفاده شود، فضای ویژگی متناظر، یک فضای هیلبرت نامتناهی است. دسته‌کننده ی بیشترین حاشیه، خوش ترتیب است، بنابراین ابعاد نامتناهی، نتیجه را خراب نمی‌کند. هسته‌های متداول به صورت زیر هستند:

  • چندجمله‌ای (همگن): {\displaystyle k(\mathbf {x_{i}} ,\mathbf {x_{j}} )=(\mathbf {x_{i}} \cdot \mathbf {x_{j}} )^{d}}
  • چندجمله‌ای (ناهمگن): {\displaystyle k(\mathbf {x_{i}} ,\mathbf {x_{j}} )=(\mathbf {x_{i}} \cdot \mathbf {x_{j}} +1)^{d}}
  • گوسیین Radial Basis Function:  {\displaystyle k(\mathbf {x_{i}} ,\mathbf {x_{j}} )=\exp(-\gamma \|\mathbf {x_{i}} -\mathbf {x_{j}} \|^{2})}، for {\displaystyle \gamma >0.} Sometimes parametrized using {\displaystyle \gamma =1/{2\sigma ^{2}}}
  • تانژانت هذلولی: {\displaystyle k(\mathbf {x_{i}} ,\mathbf {x_{j}} )=\tanh(\kappa \mathbf {x_{i}} \cdot \mathbf {x_{j}} +c)}، for some (not every) {\displaystyle \kappa >0} and {\displaystyle c<0}

هسته با انتقال {\displaystyle \varphi (\mathbf {x_{i}} )} با تساوی {\displaystyle k(\mathbf {x_{i}} ,\mathbf {x_{j}} )=\varphi (\mathbf {x_{i}} )\cdot \varphi (\mathbf {x_{j}} )} در ارتباط است. همچنین مقدار wدر فضای انتقال یافته برابر{\displaystyle \textstyle \mathbf {w} =\sum _{i}\alpha _{i}y_{i}\varphi (\mathbf {x} _{i}).} است. ضرب نقطه‌ای با w می‌تواند توسط هسته محاسبه شود یعنی {\displaystyle \textstyle \mathbf {w} \cdot \varphi (\mathbf {x} )=\sum _{i}\alpha _{i}y_{i}k(\mathbf {x} _{i},\mathbf {x} )}. به هر حال در حالت عادی w’ وجود ندارد، به‌طوری‌که {\displaystyle \mathbf {w} \cdot \varphi (\mathbf {x} )=k(\mathbf {w'} ,\mathbf {x} ).}

 

منبع

 

 

ماشین بردار پشتیبان (svm) قسمت 1
ماشین بردار پشتیبان (svm) قسمت 2
ماشین بردار پشتیبان (svm) قسمت 3

/0 دیدگاه /توسط

یادگیری ماشین قسمت 3

یادگیری ماشین(Machine learning) موضوع داغی است که اخیرا با نام های بزرگی چون گوگل و فیس بوک ساخته شده و با الگوریتم های بسیار پیچیده ای که بعضی اوقات مانند داستان های علمی تخیلی به نظر می رسند پیوند خورده است. حقیقت این است که یادگیری ماشین یک مجموعه بسیار کاربردی و کاربردی از تکنیکهایی است که قطعا کاربرد خاصی در کسب و کار شما نیز دارد.یکی از آخزین دستاوردهای یادگیزی ماشین را در این خبر علمی بخوانید.

یادگیری ماشین چیست؟

تعریف عمومی از یادگیری ماشین  آن است که توسط دانشمند کامپیوتر آرتور ساموئل در سال ۱۹۵۹ داده شده است:

یک رشته علمی است که به کامپیوترها قابلیت یادگیری می دهد بدون آنکه مشخصا برای آن کار برنامه ریزی شده باشند.

این یک پاسخ مفهومی ساده است، اما بطور مشخص، فرآیند “یادگیری ماشین” چیست؟ خروجی آن چیست؟ و چگونه می توان آن را به داده های شما اعمال کرد؟ در این مقاله  تلاش خواهیم کرد تا به تمام این سوالات به طور ساده پاسخ دهیم، اما اولا، تعریف دقیق تر زیر را ارائه خواهیم کرد:

یادگیری ماشین فرآیند استفاده از داده ها  است  که به طور خودکار یک مدل می سازد ، که به عنوان ورودی از مجموعه ای از ویژگی های شناخته شده استفاده می کند  و به عنوان خروجی چیزی به عنوان  پیش بینی ارائه می دهد.

برخی اصطلاحات

مدل

خروجی تکنیک یادگیری ماشین، یک مدل است. مدل ها اشکال مختلف می گیرند و انواع مختلف مدل ها در انواع مختلفی از مشکلات کاربرد دارند، اما به طور کلی یک مدل یک تابع ریاضی است که تعدادی از ورودی ها را می گیرد و پیش بینی برخی از مقادیر را  ارانه می دهد که برای اندازه گیری به آسانی قابل دسترس نیستند. حال  چند نمونه از مدل ها   را معرفی می کنیم:

یک معادله که به عنوان ورودی ویژگی های مختلف یک متقاضی وام (مثلا درآمد، بدهی های برجسته، مبلغ درخواست شده و غیره) را در نظر می گیرد و به عنوان یک خروجی اطمینان می دهد که وام دهنده به صورت پیش فرض وام را خواهد داد.

معادله ای که به عنوان ورودی مقدار رنگ پیکسل های یک عکس را می گیرد و به عنوان خروجی شناسایی شیء موجود در عکس را می دهد.

معادله ای که به عنوان ورودی وضعیت کنونی هیئت مدیره Go را می دهد و به عنوان خروجی نشانگر حرکتی است که بهترین شانس برنده شدن در بازی را به ارمغان می آورد.

بدیهی است که این معادلات به نظر بسیار متفاوت هستند و  در مقالات بعدی در  مورد برخی از انواع مختلف مدل های یادگیری ماشین صحبت خواهیم کرد. یادگیری ماشین فرآیند استفاده از داده ها برای ساختن مدل به طور خودکار است.

ویژگی ها

ویژگی های ورودی  مدل ماشین آموخته شده :

آنها هر قطعه ای از اطلاعات هستند که ممکن است برای پیش بینی مفید باشند. در مثال بالا، پیش بینی پیش فرض وام، درآمد، بدهی های بزرگ، مبلغ درخواست شده، همه ویژگی ها هستند. ممکن است بسیاری از ویژگی های دیگر وجود داشته باشد که می تواند مفید باشد و بعضی از آنها ممکن است ترکیبی از ویژگی های دیگر باشد؛ برای مثال، نسبت درآمد به بدهی، یا امتیاز اعتباری (که البته خروجی یک مدل متفاوت از جمله بسیاری از این ویژگی های مشابه است)

بیش برازش overfitting

برازش مدل شما به نوفه های تصادفی در  مجموعه داده های شماست. معمولا نتیجه یک مدل پیچیده؛ پیچیده خواهد شد؛ برای مثال، داشتن پارامترهای ورودی بیش از حد نسبت به تعداد مشاهدات نسبتا کم. چندین تکنیک برای جلوگیری از بیش برازش overfitting وجود دارد؛ یکی از روش های معمول برای این کار cross validation اعتبار سنجی متقابل است که در آن یک دوره جریمه های اضافی برای دادن اولویت به مدل هایی که از پارامترهای کمتری استفاده می کنند، گنجانده شده است.

طبقه بندی مشکلات یادگیری ماشین

سه طبقه بندی اصلی از وظایف یادگیری ماشین وجود دارد:

  • یادگیری تحت نظارت: مدل با استفاده از یک مجموعه شناخته شده “داده های آموزشی” ساخته شده است که شامل تمام ویژگی ها و همچنین مقادیر شناخته شده (“برچسب ها”) خروجی است که ما در حال تلاش برای مدل سازی آن هستیم. هدف از تکنیک های یادگیری تحت نظارت، رسیدن به یک مدل است که ویژگی های ورودی را برحسب برچسب ها نشان می دهد.
  • یادگیری بدون نظارت: خروجی این الگوریتم یادگیری،  برچسب ها  نیستند؛ هدف این روش کشف ساختار ناشناخته مانند خوشه ها clutsters و یا الگوهای دیگر است.
  • یادگیری تقویتی: الگوریتم پاداش و مجازات را بر اساس موفقیت آن در دستیابی به یک هدف خاص به ارمغان می آورد – به عنوان مثال، یک الگوریتم Go برای تغییرات در یک مدل که باعث افزایش نسبت زمان برنده شدن مدل و مجازات برای تغییراتی که قصد کاهش آن را دارد.این  الگوریتم قصد دارد پاداش را به حداکثر و مجازات را به حداقل برساند.

وظایف همچنین می تواند بر اساس خروجی مورد نظر از مدل یادگیری طبقه بندی شود. سه تا از رایج ترین ها عبارتند از:

طبقه بندی: داده ها به دو یا چند کلاس یا “برچسب ها” تقسیم می شوند (مثلا “hotdog” در مقابل “not hotdog “) و هدف عمل یادگیری این است که یک مدل تولید کند که ورودی ها را به یکی یا بیشتر از این برچسبها اختصاص دهد.

رگرسیون: خروجی یک  عدد پیوسته (به عنوان مثال قیمت کالای خاص، تولید یک چاه نفت ثابت شده) به جای طبقه بندی گسسته است، و  همچنین فراهم سازی مدل و برآورد خروجی هدف.

خوشه بندي: آنالوگ بدون نظارت برای طبقه بندي؛ ورودی ها باید به گروه ها تقسیم شوند، اما قبل از ساخت مدل، گروه ها شناخته نمی شوند.مثال کاربرد: پیش بینی قیمت خانه

منبع

آشنایی با الگوریتم های ضروری یادگیری ماشین

داده ها در اعماق زندگی روزانه ما ریشه دوانده اند، از خرید روزانه تا انتخاب مدرسه و پزشک و مسافرت های ما امروزه داده محور شده اند. این امر نیاز به الگوریتم ها و روشهای هوشمند پردازش داده و یادگیری ماشین را صد چندان کرده است .

انواع الگوریتم های یادگیری ماشین

سه نوع اصلی الگوریتم های یادگیری ماشین از قرار زیرند :

  • یادگیری نظارت شده (هدایت شده – Supervised Learning) : در این نوع از الگوریتم ها که بار اصلی یادگیری ماشین را بر دوش می کشند (از لحاظ تعداد الگوریتم های این نوع)، با دو نوع از متغیرها سروکار داریم . نوع اول که متغیرهای مستقل نامیده میشوند، یک یا چند متغیر هستند که قرار است بر اساس مقادیر آنها، یک متغیر دیگر را پیش بینی کنیم. مثلا سن مشتری و تحصیلات و میزان درآمد و وضعیت تاهل برای پیش بینی خرید یک کالا توسط یک مشتری ، متغیرهای مستقل هستند. نوع دوم هم متغیرهای وابسته یا هدف یا خروجی هستند و قرار است مقادیر آنها را به کمک این الگوریتم ها پیش بینی کنیم . برای این منظور باید تابعی ایجاد کنیم که ورودیها (متغیرهای مستقل) را گرفته و خروجی موردنظر (متغیر وابسته یا هدف) را تولید کند.
  • فرآیند یافتن این تابع که در حقیقت کشف رابطه ای بین متغیرهای مستقل و متغیرهای وابسته است را فرآیند آموزش (Training Process) می گوئیم که روی داده های موجود (داده هایی که هم متغیرهای مستقل و هم متغیرهای وابسته آنها معلوم هستند مثلا خریدهای گذشته مشتریان یک فروشگاه) اعمال میشود و تا رسیدن به دقت لازم ادامه می یابد.  نمونه هایی از این الگوریتم ها عبارتند از رگرسیون، درختهای تصمیم ، جنگل های تصادفی، N نزدیک ترین همسایه، و رگرسیون لجستیک.
  • یادگیری بدون ناظر (unsupervised learning) : در این نوع از الگوریتم ها ، متغیر هدف نداریم و خروجی الگوریتم، نامشخص است. بهترین مثالی که برای این نوع از الگوریتم ها می توان زد، گروه بندی خودکار (خوشه بندی) یک جمعیت است مثلاً با داشتن اطلاعات شخصی و خریدهای مشتریان، به صورت خودکار آنها را به گروه های همسان و هم ارز تقسیم کنیم . الگوریتم Apriori و K-Means از این دسته هستند.
  • یادگیری تقویت شونده (Reinforcement Learning) : نوع سوم از الگوریتم ها که شاید بتوان آنها را در زمره الگوریتم های بدون ناظر هم دسته بندی کرد ، دسته ای هستند که از آنها با نام یادگیری تقویت شونده یاد میشود. در این نوع از الگوریتم ها، یک ماشین (در حقیقت برنامه کنترل کننده آن)، برای گرفتن یک تصمیم خاص ، آموزش داده می شود و ماشین بر اساس موقعیت فعلی (مجموعه متغیرهای موجود) و اکشن های مجاز (مثلا حرکت به جلو ، حرکت به عقب و …) ، یک تصمیم را می گیرد که در دفعات اول، این تصمیم می تواند کاملاً تصادفی باشد و به ازای هر اکشن یا رفتاری که بروز می دهد، سیستم یک فیدبک یا بازخورد یا امتیاز به او میدهد و از روی این فیدبک، ماشین متوجه میشود که تصمیم درست را اتخاذ کرده است یا نه که در دفعات بعد در آن موقعیت ، همان اکشن را تکرار کند یا اکشن و رفتار دیگری را امتحان کند.
  • با توجه به وابسته بودن حالت و رفتار فعلی به حالات و رفتارهای قبلی، فرآیند تصمیم گیری مارکوف ، یکی از مثالهای این گروه از الگوریتم ها می تواند باشد . الگوریتم های شبکه های عصبی هم می توانند ازین دسته به حساب آیند. منظور از کلمه تقویت شونده در نام گذاری این الگوریتم ها هم اشاره به مرحله فیدبک و بازخورد است که باعث تقویت و بهبود عملکرد برنامه و الگوریتم می شود

الگوریتم های اصلی و رایج یادگیری ماشین

  1. رگرسیون خطی
  2. رگرسیون لجستیک
  3. درخت تصمیم
  4. SVM
  5. Naive Bayes
  6. KNN
  7. K-Means
  8. جنگل تصادفی
  9. الگوریتم های کاهش ابعاد
  10. Gradient Boost & Ada Boost

منبع

یادگیری ماشین قسمت 1
یادگیری ماشین قسمت 2
یادگیری ماشین قسمت 3

/0 دیدگاه /توسط

یادگیری ماشین قسمت 1

تعریف

به عنوان یکی از شاخه‌های وسیع و پرکاربرد هوش مصنوعی، یادگیری ماشین (Machine learning) به تنظیم و اکتشاف شیوه‌ها و الگوریتم‌هایی می‌پردازد که بر اساس آنها رایانه‌ها و سامانه‌ها توانایی تعلٌم و یادگیری پیدا می‌کنند.

Machine Learning

اهداف و انگیزه‌ها

هدف یادگیری ماشین این است که کامپیوتر (در کلی‌ترین مفهوم آن) بتواند به تدریج و با افزایش داده‌ها کارایی بهتری در انجام وظیفهٔ مورد نظر پیدا کند. گسترهٔ این وظیفه می‌تواند از تشخیص خودکار چهره با دیدن چند نمونه از چهرهٔ مورد نظر تا فراگیری شیوهٔ گام‌برداری روبات‌های دوپا با دریافت سیگنال پاداش و تنبیه باشد.

طیف پژوهش‌هایی که در یادگیری ماشینی می‌شود گسترده‌است. در سوی نظری‌ی آن پژوهش‌گران بر آن‌اند که روش‌های یادگیری تازه‌ای به وجود بیاورند و امکان‌پذیری و کیفیت یادگیری را برای روش‌های‌شان مطالعه کنند و در سوی دیگر عده‌ای از پژوهش‌گران سعی می‌کنند روش‌های یادگیری ماشینی را بر مسایل تازه‌ای اعمال کنند. البته این طیف گسسته نیست و پژوهش‌های انجام‌شده دارای مولفه‌هایی از هر دو روی‌کرد هستند.

یادگیری ماشین کمک فراوانی به صرفه جویی در هزینه‌های عملیاتی و بهبود سرعت عمل تجزیه و تحلیل داده‌ها می‌کند. به عنوان مثال در صنعت نفت و پتروشیمی با استفاده از یادگیری ماشین، داده‌های عملیاتی تمام حفاری‌ها اندازه‌گیری شده و با تجزیه و تحلیل داده‌ها، الگوریتم‌هایی تنظیم می‌شود که در حفاری‌های بعدی بیشترین نتیجه و استخراج بهینه ای را داشته باشیم.

تقسیم‌بندی مسایل

یکی از تقسیم‌بندی‌های متداول در یادگیری ماشینی، تقسیم‌بندی بر اساس نوع داده‌های در اختیار عامل هوش‌مند است. به سناریوی زیر توجه کنید:

فرض کنید به تازگی رباتی سگ‌نما خریده‌اید که می‌تواند توسط دوربینی دنیای خارج را مشاهده کند، به کمک میکروفن‌هایش صداها را بشنود، با بلندگوهایی با شما سخن بگوید (گیریم محدود) و چهارپایش را حرکت دهد. هم‌چنین در جعبهٔ این ربات دستگاه کنترل از راه دوری وجود دارد که می‌توانید انواع مختلف دستورها را به ربات بدهید. در پاراگراف‌های آینده با بعضی از نمونه‌های این دستورات آشنا خواهید شد.

اولین کاری که می‌خواهید بکنید این است که اگر ربات شما را دید خرناسه بکشد اما اگر غریبه‌ای را مشاهده کرد با صدای بلند عوعو کند. فعلاً فرض می‌کنیم که ربات توانایی تولید آن صداها را دارد اما هنوز چهرهٔ شما را یادنگرفته‌است. پس کاری که می‌کنید این است که جلوی چشم‌های‌اش قرار می‌گیرید و به کمک کنترل از راه دورتان به او دستور می‌دهید که چهره‌ای که جلوی‌اش می‌بیند را با خرناسه‌کشیدن مربوط کند.

این‌کار را برای چند زاویهٔ مختلف از صورت‌تان انجام می‌دهید تا مطمئن باشید که ربات در صورتی که شما را از مثلاً نیم‌رخ ببیند بهتان عوعو نکند. هم‌چنین شما چند چهرهٔ غریبه نیز به او نشان می‌دهید و چهرهٔ غریبه را با دستور عوعوکردن مشخص می‌کنید. در این حالت شما به کامپیوتر ربات گفته‌اید که چه ورودی را به چه خروجی مربوط کند. دقت کنید که هم ورودی و هم خروجی مشخص است و در اصطلاح خروجی برچسب‌دار است. به این شیوهٔ یادگیری، یادگیری بانظارت می‌گویند.

اینک حالت دیگری را فرض کنید. برخلاف دفعهٔ پیشین که به ربات‌تان می‌گفتید چه محرکه ای را به چه خروجی ربط دهد، این‌بار می‌خواهید ربات خودش چنین چیزی را یاد بگیرد. به این صورت که اگر شما را دید و خرناسه کشید به نحوی به او پاداش دهید (مثلاً به کمک همان کنترل از راه دورتان) و اگر به اشتباه به شما عوعو کرد، او را تنبیه کنید (باز هم با همان کنترل از راه دورتان). در این حالت به ربات نمی‌گویید به ازای هر شرایطی چه کاری مناسب است، بلکه اجازه می‌دهید ربات خود کاوش کند و تنها شما نتیجهٔ نهایی را تشویق یا تنبیه می‌کنید. به این شیوهٔ یادگیری، یادگیری تقویتی می‌گویند.

در دو حالت پیش قرار بود ربات ورودی را به خروجی مرتبط کند. اما گاهی وقت‌ها تنها می‌خواهیم ربات بتواند تشخیص دهد که آنچه می‌بیند (یا می‌شنود و…) را به نوعی به آنچه پیش‌تر دیده‌است ربط دهد بدون این‌که به طور مشخص بداند آن‌چیزی که دیده شده‌است چه چیزی است یا این‌که چه کاری در موقع دیدنش باید انجام دهد. ربات هوش‌مند شما باید بتواند بین صندلی و انسان تفاوت قایل شود بی‌آنکه به او بگوییم این نمونه‌ها صندلی‌اند و آن نمونه‌های دیگر انسان. در این‌جا برخلاف یادگیری بانظارت هدف ارتباط ورودی و خروجی نیست، بلکه تنها دسته‌بندی‌ی آن‌ها است. این نوع یادگیری که به آن یادگیری بی نظارت می‌گویند بسیار مهم است چون دنیای ربات پر از ورودی‌هایی است که کسی برچسبی به آن‌ها اختصاص نداده اما به وضوح جزئی از یک دسته هستند.

یادگیری بی‌نظارت را می‌توان به صورت عمل کاهش بعد در نظر گرفت.

از آن‌جا که شما سرتان شلوغ است، در نتیجه در روز فقط می‌توانید مدت محدودی با رباتتان بازی کنید و به او چیزها را نشان دهید و نام‌شان را بگویید (برچسب‌گذاری کنید). اما ربات در طول روز روشن است و داده‌های بسیاری را دریافت می‌کند. در این‌جا ربات می‌تواند هم به خودی خود و بدون نظارت یاد بگیرد و هم این‌که هنگامی که شما او را راه‌نمایی می‌کنید، سعی کند از آن تجارب شخصی‌اش استفاده کند و از آموزش شما بهرهٔ بیش‌تری ببرد. ترکیبی که عامل هوش‌مند هم از داده‌های بدون برچسب و هم از داده‌های با برچسب استفاده می‌کند به یادگیری نیمه نظارتی می‌گویند.

یادگیری با نظارت

یادگیری تحت نظارت، یک روش عمومی در یادگیری ماشین است که در آن به یک سیستم، مجموعه‌ای از جفت‌های ورودی – خروجی ارائه شده و سیستم تلاش می‌کند تا تابعی از ورودی به خروجی را فرا گیرد. یادگیری تحت نظارت نیازمند تعدادی داده ورودی به منظور آموزش سیستم است. با این حال رده‌ای از مسائل وجود دارند که خروجی مناسب که یک سیستم یادگیری تحت نظارت نیازمند آن است، برای آن‌ها موجود نیست. این نوع از مسائل چندان قابل جوابگویی با استفاده از یادگیری تحت نظارت نیستند.

یادگیری تقویتی مدلی برای مسائلی از این قبیل فراهم می‌آورد. در یادگیری تقویتی، سیستم تلاش می‌کند تا تقابلات خود با یک محیط پویا را از طریق آزمون و خطا بهینه نماید. یادگیری تقویتی مسئله‌ای است که یک عامل که می‌بایست رفتار خود را از طریق تعاملات آزمون و خطا با یک محیط پویا فرا گیرد، با آن مواجه است. در یادگیری تقویتی هیچ نوع زوج ورودی- خروجی ارائه نمی‌شود. به جای آن، پس از اتخاذ یک عمل، حالت بعدی و پاداش بلافصل به عامل ارائه می‌شود. هدف اولیه برنامه‌ریزی عامل‌ها با استفاده از تنبیه و تشویق است بدون آنکه ذکری از چگونگی انجام وظیفه آن‌ها شود.

تعریف ریاضی مسایل یادگیری ماشین

یادگیری با نظارت

در این مدل یادگیری مثال‌های آموزشی به صورت جفت‌های (x^{i},y^{i}) که در آن هر نمونه به همراه بر چسب آن داده شده‌اند و i اندیس هر مثال در مجموعه مثال‌های آموزشی D است. هدف در این یادگیری بدست آوردن تابع f است که بتواند برای نمونه‌های ورودی دیده نشده x بر چسب مناسب را برگرداند(f(x) = y). نمونه و بر چسب هر دو می‌توانند یک بردار باشند. اگر بر چسب یک عدد حقیقی باشد مسئله پیش روی ما رگرسیون نامیده می‌شود. اگر بر چسب یک عدد صحیح باشد به مسئله دستبه بندی گفته می‌شود.

 

یکی از انواع یادگیری از داده‌ها

منبع

یادگیری ماشین قسمت 1
یادگیری ماشین قسمت 2
یادگیری ماشین قسمت 3

/0 دیدگاه /توسط

تعریف رگرسیون خطی (Linear Regression) قسمت 5

برآورد پارامترهای رگرسیون خطی ساده

به منظور برآورد پارامترهای رگرسیون خطی ساده، کافی است تابع مجموع مربعات خطا را کمینه کرد. برای این کار مراحل زیر باید طی شوند:

  • محاسبه مجموع توان دوم خطا

∑(yi−(β^0+β^1xi))2

  • مشتق مجموع مربعات خطا برحسب پارامتر β^0

∑(−yi+β^0+β^1xi)

  • برابر قرار دادن مشتق با صفر به منظور پیدا کردن نقاط کمینه

∑(−yi+β^0+β^1xi)=0

  • پیدا کردن ریشه برای معادله حاصل برحسب β^0

β^0=y¯−β^1x¯

  • مشتق مجموع مربعات خطا بر حسب پارامتر  β^1

∑(−2xiyi+2β^0xi+2β^1xi2)

  • جایگذاری β^0 و پیدا کردن ریشه برای معادله حاصل برحسب β^1

−∑(xiyi+(y¯−β^1x¯)∑xi+β^1∑xi2)=0

β1^=∑(xi−x¯)(yi−y¯)∑(xi−x¯)2

به این ترتیب برآورد پارامترهای مدل خطی به صورت زیر خواهند بود.

β1^=∑(xi−x¯)(yi−y¯)∑(xi−x¯)2

β0^=y¯−β1^x¯

که در آن x¯  و y¯ میانگین x و y هستند.

برای راحتی محاسبات، می‌توان برآورد β1 را به فرم دیگری نیز نوشت:

β1^=n(xy¯−x¯y¯))(n−1)σx2

که منظور از xy¯ میانگین حاصلضرب x و y بوده و σx2 نیز بیانگر واریانس مقدارهای x است.

اگر y^ مقدار برآورد برای متغیر وابسته باشد، می‌توانیم آن را میانگین مشاهدات برای متغیر وابسته به ازای مقدار ثابت متغیر مستقل در نظر گرفت. پس با فرض اینکه میانگین جمله خطا نیز صفر است، خواهیم داشت:

y^=E(Y|X=x)=β0^+β1^x

که در آن E(Y|X=x) نشان‌دهنده امید ریاضی (متوسط) شرطی است و همچنین  β0^ و β^1 برآوردهای مربوط به هر یک از پارامترها هستند.

نکته: به راحتی دیده می‌شود که میانگین مربوط به متغیر مستقل و وابسته روی خط رگرسیون قرار دارند. یعنی این نقطه در معادله خط رگرسیون صدق می‌کند. زیرا با توجه به محاسبه β0 داریم:

β0^=y¯−β1^x¯→Y¯=β^0+β^1X¯

مثال

اطلاعات مربوط به ۵۰ خانه شامل قیمت (به میلیون ریال) و متراژ (متر مربع) در شهر تهران جمع‌آوری شده است. این اطلاعات را می‌توانید با قالب اکسل از اینجا دریافت کنید.

با توجه به ضریب همبستگی بین این دو متغیر که برابر با 0.9891 است،‌ مشخص است که رابطه خطی شدیدی بینشان برقرار است. اگر فرض کنیم قیمت خانه متغیری وابسته به متراژ است، محاسبات اولیه برای برآورد پارامترهای مدل رگرسیونی در جدول زیر قرار گرفته.

X¯ Y¯ XY¯ σX2
84.9 451.136 40350.6 411.724

بر این اساس برآورد پارامترهای مدل خطی به صورت β^0=19.965 و β^1=5.078  خواهد بود. در نتیجه می‌توان معادله مربوط برآورد مقدار متغیر وابسته را به صورت زیر نوشت:

yi^=19.965+5.078xi

پس اگر لازم باشد که ارزش خانه‌ای با متراژ 61 متر محاسبه شود، کافی است در معادله بالا برای xi‌ مقدار 61 را جایگزین کرده،‌ مقدار y^i را بدست آوریم که برابر با 329.758 میلیون ریال است. در تصویر زیر نمودار مربوط به داده‌ها و خط رگرسیون دیده می‌شود.

yi^=19.965+5.078(61)=329.758

 

 

تعریف رگرسیون خطی (Linear Regression) قسمت 1
تعریف رگرسیون خطی (Linear Regression) قسمت 2
تعریف رگرسیون خطی (Linear Regression) قسمت 3
تعریف رگرسیون خطی (Linear Regression) قسمت 4
تعریف رگرسیون خطی (Linear Regression) قسمت 5
تعریف رگرسیون خطی (Linear Regression) قسمت 6
تعریف رگرسیون خطی (Linear Regression) قسمت 7

/0 دیدگاه /توسط

تعریف رگرسیون خطی (Linear Regression) قسمت 4

مفهوم رگرسیون

در آمار، رگرسیون خطی یک روریکرد مدل خطی بین متغیر «پاسخ» (Response) با یک یا چند متغیر «توصیفی» (Explanatory) است. اغلب برای کشف مدل رابطه‌ی خطی بین متغیرها از رگرسیون (Regression) استفاده می‌شود. در این حالت فرض بر این است که یک یا چند متغیر توصیفی که مقدار آن‌ها مستقل از بقیه متغیرها یا تحت کنترل محقق است، می‌تواند در پیش‌بینی متغیر پاسخ که مقدارش وابسته به متغیرهای توصیفی و تحت کنترل محقق نیست، موثر باشد. هدف از انجام تحلیل رگرسیون شناسایی مدل خطی این رابطه‌ است.

در ادامه از  متغیر وابسته به جای متغیر پاسخ و متغیر مستقل به جای متغیر توصیفی استفاده می‌کنیم.

از آنجایی که ممکن است علاوه بر متغیرهای مستقل، عوامل زیاد و ناشناخته‌ دیگری نیز در تعیین مقدار متغیر وابسته نقش داشته باشند، مدل رگرسیونی را با مناسب‌ترین تعداد متغیر مستقل در نظر گرفته و میزان خطا را به عنوان نماینده عوامل تصادفی دیگری که قابل شناسایی نبودند در نظر می‌گیریم که انتظار است کمتر در تغییرات متغیر وابسته نقش داشته باشند.

تاریخچه رگرسیون

واژه رگرسیون برای اولین بار در مقاله‌ معروف فرانسیس گالتون دیده شد که در مورد قد فرزندان و والدینشان بود. این واژه به معنی بازگشت است. او در مقاله خود در سال 1۸۷۷ اشاره می‌کند که قد فرزندان قد بلند به میانگین قد جامعه میل می‌کند. او این رابطه را «بازگشت» (Regress) نامید.

هر چند واژه رگرسیون در شاخه علوم زیستی معرفی شد ولی آنچه امروزه به نام رگرسیون می‌شناسیم،‌ روشی است که توسط «گاوس» (Gauss) در سال 1۸۰۹ معرفی شد تا به کمک آن پارامترهای مجهول رابطه بین مدار سیاره‌های منظومه شمسی را برآورد کند.

بعدها روش گاوس توسط پیرسون (Pearson) توسعه یافت و با مفاهیم آماری آمیخته شد. همچنین پیرسون توزیع توام متغیر وابسته و مستقل را توزیع گاوسی در نظر گرفت. بعدها «فیشر» (R. A. Fisher) توزیع متغیر وابسته به شرط متغیر مستقل را توزیع گاوسی محسوب کرد.

مدل رگرسیون خطی ساده

اگر برای شناسایی و پیش‌بینی متغیر وابسته فقط از یک متغیر مستقل استفاده شود، مدل را «رگرسیون خطی ساده» (Simple Linear Regression) می‌گویند. فرم مدل رگرسیون خطی ساده به صورت زیر است:

Y=β0+β1X+ϵ

همانطور که دیده می‌شود این رابطه، معادله یک خط است که جمله خطا یا همان ϵ‌ به آن اضافه شده. پارامترهای این مدل خطی عرض از مبدا (β0) و شیب خط (β1) است. شیب خط در حالت رگرسیون خطی ساده، نشان می‌دهد که میزان حساسیت متغیر وابسته به متغیر مستقل چقدر است. به این معنی که با افزایش یک واحد به مقدار متغیر مستقل چه میزان متغیر وابسته تغییر خواهد کرد. عرض از مبدا نیز بیانگر مقداری از متغیر وابسته است که به ازاء مقدار متغیر مستقل برابر با صفر محاسبه می‌شود. به شکل دیگر می‌توان مقدار ثابت یا عرض از مبدا را مقدار متوسط متغیر وابسته به ازاء حذف متغیر مستقل در نظر گرفت.

برای مثال فرض کنید کارخانه‌ای می‌خواهد میزان هزینه‌هایش را براساس ساعت کار برآورد کند. شیب خط حاصل از برآورد نشان می‌دهد به ازای یک ساعت افزایش ساعت کاری چه میزان بر هزینه‌هایش افزوده خواهد شد. از طرفی عرض از مبدا خط رگرسیون نیز هزینه ثابت کارخانه حتی زمانی که ساعت کاری نیست نشان می‌دهد. این هزینه را می‌توان هزینه‌های ثابت مانند دستمزد نگهبانان و هزینه روشنایی فضای کارخانه فرض کرد.

گاهی مدل رگرسیونی را بدون عرض از مبدا در نظر می‌گیرند و  β0=0 محسوب می‌کنند. این کار به این معنی است که با صفر شدن مقدار متغیر مستقل، مقدار متغیر وابسته نیز باید صفر در نظر گرفته شود. زمانی که محقق مطمئن باشد که که خط رگرسیون باید از مبدا مختصات عبور کند، این گونه مدل در نظر گرفته می‌شود. فرم مدل رگرسیونی در این حالت به صورت زیر است:

Y=β1X+ϵ

از آنجایی که پیش‌بینی رابطه بین متغیر وابسته و مستقل به شکل دقیق نیست، جمله خطا را یک «متغیر تصادفی» (Random Variable) با میانگین صفر در نظر می‌گیرند تا این رابطه دارای اریبی نباشد.

باید توجه داشت که منظور از رابطه خطی در مدل رگرسیون، وجود رابطه خطی بین ضرایب است نه بین متغیرهای مستقل. برای مثال این مدل y=β0+β1×2+ϵ را نیز می‌توان مدل خطی در نظر گرفت در حالیکه مدل y=β0xβ1+ϵ دیگر خطی نیست و به مدل نمایی شهرت دارد.

همچنین در فرضیات این مدل، خطا یک جمله تصادفی است و تغییرات آن مستقل از متغیر X‌ است. به این ترتیب مقدار خطا وابسته به مقدار متغیر مستقل نیست.

در رگرسیون خطی سعی می‌شود، به کمک معادله خطی که توسط روش رگرسیون معرفی می‌شود، برآورد مقدار متغیر وابسته به ازای مقدارهای مختلف متغیر مستقل توسط خط رگرسیون بدست آید. به منظور برآورد پارامترهای مناسب برای مدل، کوشش می‌شود براساس داده‌های موجود، مدلی انتخاب می‌شود که کمترین خطا را داشته باشد.

روش‌های مختلفی برای تعریف خطا و حداقل کردن آن وجود دارد. معیاری که در مدل رگرسیون خطی ساده به کار می‌رود، کمینه کردن مجموع مربعات خطا است. از آنجایی که میانگین مقدارهای خطا صفر در نظر گرفته شده است، می‌دانیم زمانی مجموع مربعات خطا، حداقل ممکن را خواهد داشت که توزیع داده‌ها نرمال باشند. در نتیجه، نرمال بودن داده‌های متغییر وابسته یا باقی‌مانده‌ها یکی از فرضیات مهم برای مدل رگرسیونی خطی ساده است.

شکل زیر به منظور توضیح نرمال بودن مقدار خطا ترسیم شده است. در هر مقدار از متغیر مستقل ممکن است بیش از یک مقدار برای متغیر وابسته مشاهده شود. مقدار پیش‌بینی شده برای هر یک از این مقدارها ثابت است که توسط معادله خط رگرسیون برآورد می‌شود.

برای مثال تعدادی مقدار برای متغیر وابسته براساس مقدار x=65 وجود دارد که شکل توزیع فراوانی آن‌ها به صورت نرمال با میانگین β0+β1×65 است. همچنین برای نقطه ۹۰ نیز مقدار پیش‌بینی یا برآورد برای متغیر وابسته به صورت β0+β1×90 خواهد بود. در هر دو حالت واریانس خطا یا واریانس مقدارهای پیش‌بینی‌شده (پهنای منحنی زنگی شکل)  ثابت است.

در تصویر زیر چهار نقطه از مشاهدات (x,y) به همراه خط رگرسیون دیده می‌شوند که در آن خط رگرسیون با رنگ آبی، نقطه‌های مربوط به مشاهدات با رنگ قرمز و فاصله هر نقطه از خط رگرسیون (خطای برآورد) با رنگ سبز نشان داده شده است.

 

Linear_least_squares
نمودار نقطه‌ای متغیر مستقل و وابسته،‌ میزان خطا و خط رگرسیون

برای برآورد کردن پارامترهای مدل رگرسیونی باید معادله خطی یافت شود که از بین همه خطوط دیگر دارای کمترین مجموع توان دوم خطا باشد. یعنی ∑ϵ2 برای آن از بقیه خطوط کمتر باشد.

points_for_linear_regression
خطوط مناسب برای بیان رابطه بین متغیر مستقل و وابسته

به نظر شما در تصویر بالا،‌ کدام خط دارای مجموع مربعات خطای کمتری است؟ امکان تشخیص بهترین خط بدون استفاده از ابزارهای محاسباتی امکان‌پذیر نیست.

 

تعریف رگرسیون خطی (Linear Regression) قسمت 1
تعریف رگرسیون خطی (Linear Regression) قسمت 2
تعریف رگرسیون خطی (Linear Regression) قسمت 3
تعریف رگرسیون خطی (Linear Regression) قسمت 4
تعریف رگرسیون خطی (Linear Regression) قسمت 5
تعریف رگرسیون خطی (Linear Regression) قسمت 6
تعریف رگرسیون خطی (Linear Regression) قسمت 7

/0 دیدگاه /توسط