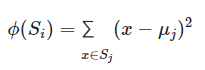رباتهای سلامتی
رباتهایی که در زمینه سلامتی فعالیت می کنند دو کاربرد عمده دارند. یک دسته از این رباتها به افراد با بیماری های مختلف، مثلا مبتلایان به ام اس کمک می کنند و دسته ای دیگر، به زیرمجموعه های سیستمهای بهداشتی و سلامتی مثلا بیمارستآنها و داروخانه ها کمک می کنند.
اتوماسیون خانگی برای افراد مسن و یا معلول
رباتهایی که در اتوماسیون خانگی مورداستفاده قرار میگیرند در طول زمان، از دستیار های ساده ای مانند Handy 1 به رباتهای نیمه خودگردان پیشرفته ای مانند FRIEND تبدیل شدهاند که میتواند افراد مسن یا معلول را در انجام کارهای روزمره شان کمک کند.
امروزه، سن متوسط جمعیت در بسیاری از کشور ها، بهخصوص در ژاپن در حال افزایش است. معنای این نکته این است تعداد افراد مسنی که به مراقبت احتیاج دارند در حال زیاد شدن است اما تعداد افراد جوان که برای مراقبت از آنها لازم است به نسبت کمتر است. انسانها همواره نقش بهترین مراقبت کننده را بازی خواهند کرد اما در صورتی که انسانها در دسترس نباشند، این رباتها هستند که به طور تدریجی این مسئولیت را به عهده خواهند گرفت.
FRIEND یک ربات نیمه خودگردان است که برای کمک به افراد مسن و معلول در انجام کار های روزانه شان، مثلا درست کردن غذا و سرو آن، طراحی شده است. FRIEND برای بیمارانی که از پاراپلژی(ناتوانی کامل پا و تنه در حرکت) رنج می رند، دچار بیماری های عضلانی هستند و یا به دلیل سکته و موارد دیگر دچار فلج کامل عضلات شدهاند کمک می کند تا بدون نیاز به پرستار، بتوانند کارهای مختلفی را انجام دهند.

یک نمونه از ربات های پیشرفته مشهور به Friend
داروخانه ها
شرکت Script Pro رباتی را تولید کرده که به داروخانه ها کمک می کند تا نسخه هایی را که شامل جامدات خوراکی یا قرص های دارویی مختلف هستند، بپیچند.
داروساز یا تکنیسین داروخانه، اطلاعات نسخه را در سیستم اطلاعات داروخانه وارد می کند. سیستم با مشخص کردن اینکه آیا دارو های ذکر شده در داخل ربات موجود هستند یا خیر، اطلاعات را به ربات می فرستد تا نسخه را بپیچد. این ربات سه ظرف مخصوص دارو با اندازه های مخصوص برای پر کردن دارد که اندازه آنها از اندازه قرص ها تبعیت می کند. زمانی که موجودی دارو های داخل ربات در حال پر شدن هستند، تکنیسین ربات یا مسئول داروخانه اندازه ظرف مورد نیاز را بر اساس اندازه قرص ها تعیین می کند. بعد از اینکه ظرف مخصوص دارو پر شد، یک نوار نقاله آن را به یک نگه دارنده تحویل می دهد. در این قسمت نگه دارنده، ظرف دارو را در جای خود نگه می دارد و در عین حال، با چرخاندن آن حول محور مرکزی، امکان چسباندن برچسب نام بیمار را بر روی ظرف را فراهم می کند. پس از اینکه ربات برچسب لازم را بر روی طرف دارو چسباند، ظرف مجددا به نوار نقاله دیگری سپرده می شود و این بار ظرف حاوی دارو به شیاری که در بالای آن نام بیمار با استفاده از چراغ های LED نمایش داده شده است فرستاده می شود. در این حالت، داروساز یا تکنیسین داروخانه، محتویات ظرف را چک می کند تا مطمئن شود، داروی صحیح برای فرد صحیح پر شده است و سپس ظرف را بسته بندی می کند و آن را به قسمت جلو داروخانه می فرستد تا به بیمار تحویل داده شود. این ربات از نظر زمانی بسیار پربازده است.
ربات Robot RX محصول شرکت McKesson یکی دیگر از محصولات رباتیک مربوط به سلامتی است که به داروخانه ها کمک می کند در طول روز هزاران دارو را بدون هیچ خطا یا با خطایی بسیار کم، توزیع کنند. این ربات میتواند عرضی معادل 10 فوت و طولی معادل 30 فوت داشته باشد و صدها نوع داروی مختلف را با دوز های متفاوت در خود جای می دهد. با کمک این ربات، داروخانه در منابع مختلف مثلا نیروی انسانی صرفه جویی می کند.
این دستگاه از یک هِد الکترومکانیکی در کنار یک سیستم پنوماتیکی( با فشار هوا) استفاده می کند تا دارو های مختلف با دوز های متفاوت را بردارد و آن را به محل تحویل یا به محل انبار دارو های خود منتقل کند. هِد دستگاه در راستای یک محور حرکت می کند و در عین حال میتواند 180 درجه بچرخد تا دارو های مختلف را از قسمت های مختلف بردارد. در طول این فرآیند، ربات از فنّاوری بارکد استفاده می کند تا مطمئن شود در حال برداشتن داروی صحیح است. سپس ربات این دارو را به سبد مخصوص بیمار که بر روی یک نوار نقاله قرار گرفته است منتقل می کند. وقتی سبد با همه داروهایی که بیمار به آن نیاز دارد پر شد، سبد آزاد می شود و از طریق نوار نقاله به دست تکنیسین داروخانه می رسد که منتظر است تا آن را به سبدی دیگر منتقل کرده و به طبقه اصلی داروخانه ببرد.
رباتهای تحقیقاتی
اگرچه امروزه بیشتر رباتها در منازل یا کارخانه ها مورداستفاده قرار میگیرند و کار های بسیار مفیدی را انجام میدهند، انواع جدید رباتها در آزمایشگاه های مختلفی در سرتاسر جهان در حال توسعه یافتن هستند. بیشتری تحقیقاتی که در حاضر در زمینه رباتیک انجام می شود بر روی کار های مخصوص به یک صنعت خاص متمرکز نیست بلکه عمده تحقیقات در زمینه ساخت انواع جدیدی از رباتها و روشهای مختلف برای طراحی و تولید آنها می باشد. انتظار میرود زمانی که ساخت انواع جدید رباتها در مقیاس بزرگ عملی شود، آنها بتوانند مسائل دنیای واقعی را حل کنند.
رباتهای بیونیک و بیومیمتیک(زیست تقلید)
یکی از نگرش های موجود برای طراحی رباتها، این است که آنها را بر اساس حیوانات طراحی کنند. رباتی به نام بیونیک کانگورو با مطالعه و اِعمال فیزیولوژی و روشهای حرکتی کانگورو طراحی و ساخته شد.
نانو رباتها
نانو رباتیک، یک زمینه فنّاوری در حال ظهور است که هدف آن ساخت ماشینها یا رباتهایی است که اجزای آنها ابعادی نزدیک یا برابر با ابعاد میکروسکوپی نانومتر(10−9 متر) دارند. این رباتها که با نام نانوبات نیز شناخته میشوند از ماشینهای مولکولی ساخته میشوند. تاکنون محققان بیشتر توانسته اند قطعات مختلف این سیستمهای پیچیده مانند یاتاقان، سنسورها و یا موتور های مولکولی مصنوعی را تولید کنند، البته نانو رباتهای کامل نیز ساختهشدهاند که برای نمونه میتوان به شرکتکنندگان مسابقات روبوکاپ نانورباتها اشاره کرد.
محققان همچنین امیدوارند تا بتوان رباتهای کاملی را بسازند که به اندازه ویروس ها یا باکتری ها باشند و بتوانند کار های مختلفی را در مقیاس بسیار کوچک انجام دهند. از کاربرد ها احتمالی این گونه رباتها میتوان به عمل جراحی در مقیاس میکروسکوپی (در مقیاس سلول های بدن)، استفاده از چندین نانو ربات در کنار هم (Utility Fog) و کاربردهای بسیار زیاد در تولید، تسلیحات جنگی و نظافت اشاره کرد. برخی افراد معتقدند اگر نانو رباتهایی وجود داشته باشد که بتوانند تکثیر شوند، سناریوی Grey goo اتفاق میافتد. در این سناریو، نانورباتها به قدری تکثیر میشوند که به این شیوه همه چیز را در جهان می بلعند و اکوسیستم را با تغییر هر آنچه برای آنها نامطبوع است تخریب خواهند کرد. البته عده دیگری معتقدند چنین سناریو فرضی کاملا مهمل است.

نانو ربات Utility Fog
رباتهای شکل پذیر
تاکنون چندین محقق امکان ساخت رباتهایی را که میتوانند شکل فیزیکی خود را تغییر دهند تا برای انجام کاری خاص مناسب باشند را بررسی کردهاند که برای نمونه میتوان به ربات تخیلی T-1000 در فیلم ترمیناتور اشاره کرد. با این وجود، رباتهای واقعی اصلا به پیچیدگی T-1000 نیستند و عمدتاً از تعداد کمی اجزای مکعبی شکل تشکیل شدهاند که میتوانند نسبت به اجزای مجاورشان حرکت کنند. در صورتی که چنین رباتهایی به واقعیت تبدیل شوند، الگوریتم هایی نیز برای آنها طراحی شده است.
رباتهای نرم تن
این دسته از رباتها از بدنه های سیلیکونی و محرک های انعطاف پذیر( ماهیچه های مصنوعی پنوماتیکی، پلیمر های الکترواکتیو و فروسیال ها) ساختهشدهاند و ظاهری متفاوت نسبت به رباتهای با ساختار صلب دارند. این رباتها میتوانند رفتار ها و کاربردهای مختلفی داشته باشند.
رباتهای ازدحامی
این گونه از رباتها، از کلونی حشراتی مانند زنبورعسل و مورچه ها الهام گرفته شدهاند. محققان در حال تلاشند تا با مدل سازی رفتار زنبور ها و مورچه ها، ازدحامی از هزاران ربات کوچک بسازند که بتوانند با کمک یکدیگر، کار های مفیدی مانند پیدا کردن یک شی مخفی، نظافت و یا جاسوسی را انجام دهند. هر ربات عضو مجموعه، بسیار ساده است اما رفتار ناشی از ظهوریافتگی این مجموعه پیچیده تر است. در واقع همان طور که یک کلونی مورچه را میتوان بهعنوان یک ابر ارگانیسم در نظر گرفت که دارای هوش ازدحامی است؛ به طور مشابه نیز میتوان کل مجموعه این رباتها را بهعنوان یک مجموعه توزیع شده در نظر گرفت. بزرگترین مجموعه رباتهایی که تاکنون ساخت شدهاند شامل مجموعه iRobot، رباتهای پروژه CentiBots و مجموعه رباتهای پروژه منبع باز Micro-robotic هستند که از آنها برای تحقیق بر روی رفتار گروهی رباتها استفاده می شود. مجموعه رباتها، در برابر خرابی مقاوم تر هستند. در حالی که یک ربات بزرگ ممکن است خراب شود و یک ماموریت را به طور کامل نابود کند، یک مجموعه از رباتها، حتی با از دست دادن چند عضو نیز به کار خود ادامه خواهد داد. این ویژگی، رباتهای ازدحامی را به گزینه های هیجان انگیز و جذاب برای اکتشافات فضایی تبدیل کرده است زیرا در این گونه ماموریت ها، شکست در ماموریت معمولا هزینه های بسیار بالایی را در بر دارد.

نمایی از ریز ربات های ازدحامی یا گروهی
رباتهای رابط لمسی
رباتیک در طراحی رابط های واقعیت مجازی نیز کاربرد دارد. امروزه، رباتهای مخصوص در زمینه تحقیقات مربوط به فناوری لمسی به طور گسترده ای مورداستفاده قرار میگیرند. این رباتها، که به آنها “رابط های لمسی” گفته می شود، امکان تعامل کاربر را بهصورت لمسی با محیط های واقعی و مجازی فراهم می کنند.در واقع در این فرآیند، نیرو های رباتیکی امکان شبیهسازی خواص مکانیکی اجسام مجازی را فراهم می کنند و در نتیجه، کاربر میتواند آنها را از طریق حس لامسه خود، احساس کند.
رباتها در فرهنگ عامه
ربات در ادبیات
شخصیت های رباتی، اندروید ها ( زنان و مردان مصنوعی)، ژینوئید ها (زنان مصنوعی) و سایبورگ ها (انسانهایی که از اجزای مکانیکی مختلفی در بدن خود بهره میبرند) به رکن اساسی داستانهای علمی – تخیلی تبدیل شدهاند.
در ادبیات غربی، اولین اشاره به خدمتکار های مکانیکی در کتاب ایلیاد که توسط هومر نوشته شده مطرح می شود. در کتاب هجدهم، هفائستوس، خدای آتش با کمک رباتها زره جدیدی را برای آَشیل قهرمان می سازد. بنا به نسخه ترجمه شده توسط Rieu، “خدمتکاران طلایی به کمک اربابشان شتافتند؛ آنها شبیه به زنان واقعی بودند و نه تنها میتوانستند صحبت کنند و از اعضای بدنشان استفاده کنند بلکه، خدایان جاودان به آنها هوش عطا کرده بودند و مهارت کار دستی را به آنها آموخته بودند.” البته واضح است که از کلمات ربات یا ربات انساننما برای توصیف این خدمتکاران استفاده نشده است اما در هر حال، این خدمتکاران، دستگاههایی مکانیکی بودند که ظاهری شبیه به انسان داشتند. همان طور که گفته شد، اولین استفاده از کلمه ربات در نمایشنامه کارخانه رباتسازی روسوم که توسط کارل چاپک، نویسنده اهل جمهوری چک اتفاق افتاده است.
شاید بتوان ایزاک آسیموف (1920-1992) را پرکارترین نویسنده قرن بیستم دانست. او بیش از 500 کتاب منتشر کرد. همه آسیموف را به خاطر داستانهای علمی-تخیلیش به خاطر دارند؛ بهخصوص آن داستانهایی که مربوط به رباتها بودند. آسیموف، رباتها و تعامل آنها با جامعه را نقطه مرکزی بسیاری از داستانهای خود قرار داده بود. او با دقت فراوان مسئله دستورالعمل های ایده آلی را که ممکن بود به یک ربات داده شود تا خطرش برای انسانها کمتر شود را در نظر گرفت و در نهایت، توانست سه قانون اصلی رباتیک خود را به این ترتیب بیان کند:
- یک ربات نمیتواند به انسان صدمه بزند یا با واکنش نشان ندادن، اجازه دهد تا یک انسان صدمه ببیند
- یک ربات باید به استثنا مواردی که منجر به نقض قانون اول می شود، از دستوراتی که توسط انسان به او داده می شود اطاعت کند
- یک ربات باید تا زمانی که محافظت از خودش منجر به نقض قانون های اول و دوم نشود، از موجودیت خود محافظت کند.
او این قوانین را اولین بار در سال 1942 در داستان کوتاهی به نام Runaround معرفی کرد. البته این قوانین به طور ضمنی در چند داستان قبلی او نیز مطرحشده بودند. بعد ها، آسیموف قانون صفرم را نیز به این مجموعه اضافه کرد: “یک ربات نمیتواند به بشریت آسیب رساند یا با واکنش نشان ندادن، اجازه دهد تا بشریت آسیب ببیند.” قانون های بعدی نیز برای در نظر گرفتن این قانون، کمی تغییر کردند.
بنا به فرهنگ لغت انگلیسی آکسفورد، اولین بخش از داستان کوتاه آسیموف به نام دروغگو(1941) که در آن به قانون اول نیز به طور ضمنی اشاره می شود، اولین مورد ثبتشده استفاده از کلمه رباتیک است.نکته جالب این است که آسیموف خود از این موضوع خبر نداشت؛ او فکر می کرد این واژه که شباهت زیادی با واژه های مکانیک، هیدرولیک و واژه های مشابه دیگر که به شاخه های مختلف علوم کاربردی اشاره دارند، از قبل وجود داشته است.
ربات در فیلم ها
رباتها در فیلم های بسیاری دیده شدهاند. بیشتر رباتهایی که در سینما دیده میشوند تخیلی هستند. بهعنوان نمونه هایی از رباتهای تخیلی میتوان به رباتهای R2-D2 و C-3PO از مجموعه فیلم های جنگ ستارگان و ربات T800 در فیلم ترمیناتور اشاره کرد.

ربات T800 در مجموعه فیلم های ترمیناتور
رباتهای جنسی
مفهوم رباتهای شبیه به انسان که کارکردشان، برطرف کردن نیاز های جنسی انسان است هم باعث جلب توجه عمومی و هم باعث نگرانی های بسیاری شده است. مخالفین این مفهوم معتقدند توسعه رباتهای جنسی از نظر اخلاقی درست نیست. آنها ادعا می کنند ساخت چنین دستگاهی، آسیب های اجتماعی بسیاری را در پی خواهد داشت و باعث تحقیر زنان و کودکان خواهد شد.
مشکلاتی که در فرهنگ عامه نشان داده شده است
ترس و نگرانی از رباتها، به طور گسترده ای در کتاب ها و فیلم های مختلف بیان شده است. یکی از زمینه های معمول، تشکیل نژادی برتر از رباتهای خودآگاه و کاملا هوشمند است که برای براندازی یا نابودی انسانها تلاش می کنند. رمان فرانکنشتاین(1818) که بهعنوان اولین رمان علمی-تخیلی شناخته می شود نیز با این زمینه که یک ربات بتواند جای خالق خود را بگیرد مترادف شده است.
کار های دیگری که زمینه ای مشابه دارند شامل مرد مکانیکی، ترمیناتور، من-ربات و یا سه گانه ماتریکس هستند. برخی از رباتهای تخیلی برای کشتن و نابود کردن برنامه ریزی شدهاند؛ برخی دیگر با بهروزرسانی نرم افزار و سخت افزار خود، به هوش و تواناییهای فرا انسانی دست می یابند. نمونه های دیگری از رسانه هایی که در آن رباتها به موجودات شیطانی تبدیل میشوند شامل 2001: A Space Odyssey، Red Planet و Enthiran هستند.
بازی کامپیوتری Horizon Zero Dawn به زمینه هایی چون استفاده از رباتها بهعنوان سلاح، مسائل اخلاقی مربوط به رباتها و مسئله کنترل هوش های مصنوعی می پردازد و همچنین اثرات مثبت و یا منفی چنین فنّاوری هایی را بر روی محیط زیست را مطرح می کند.
یکی دیگر از زمینه های بسیار متداول، حس اضطراب و حتی عصبانیت انسانها در مواجه با رباتهای انساننمایی است که رفتارشان هیچگونه فرقی با انسانهای عادی ندارد. از نظر علمی به این پدیده دره وهمی گفته می شود.
اخیرا، استفاده از رباتهای هوشمند در فیلم هایی مانند A.I. Artificial Intelligence و Ex Machina و همچنین سریال تلویزیونی Westworld ( محصول سال 2016) باعث ایجاد حس همدردی مخاطبان نسبت به خود رباتها شده است.



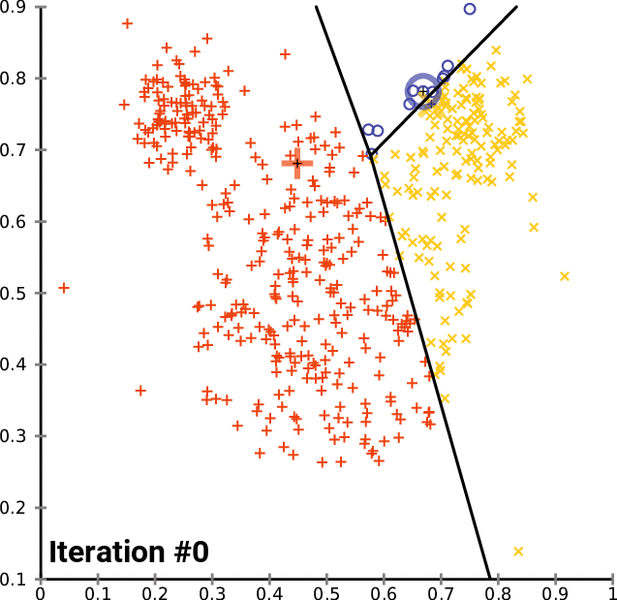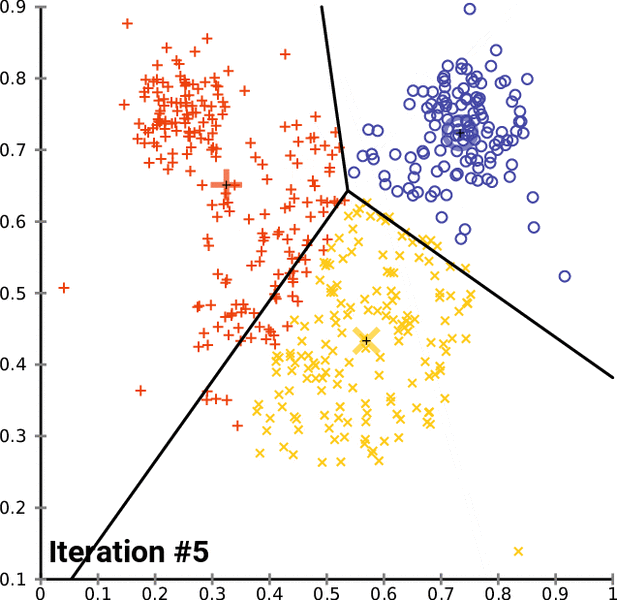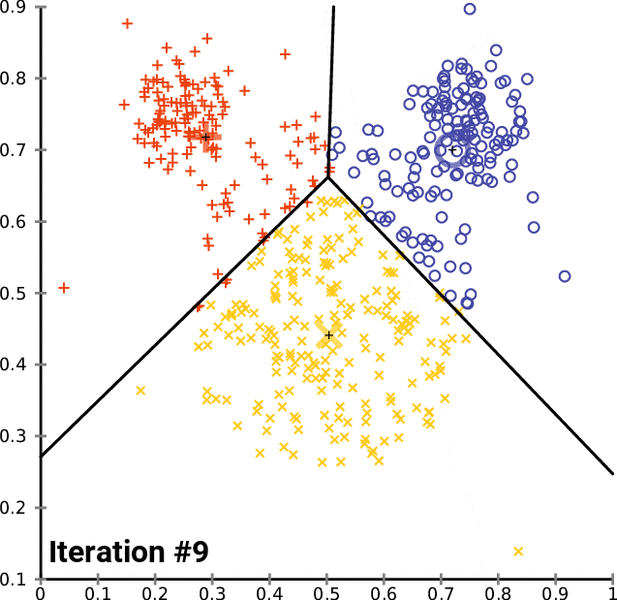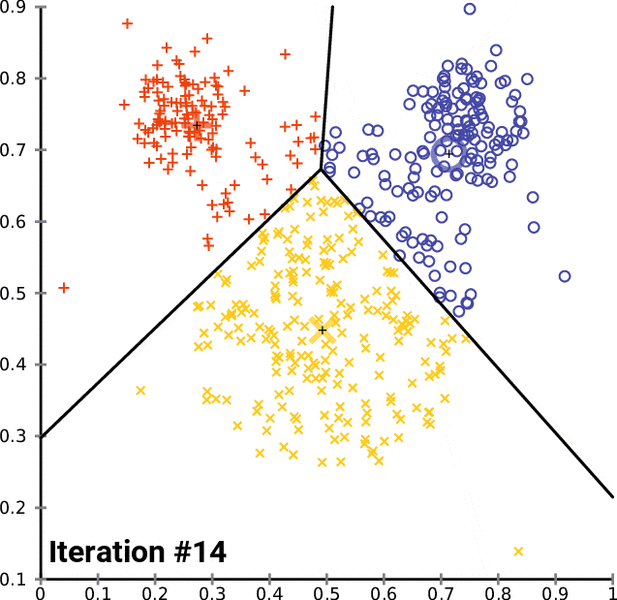
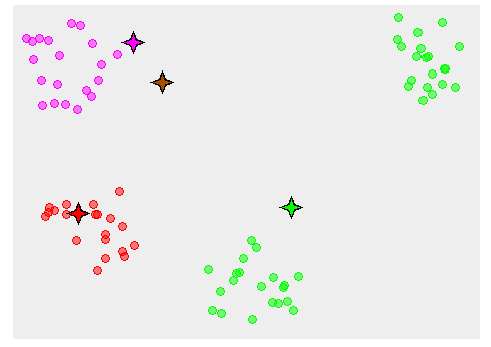
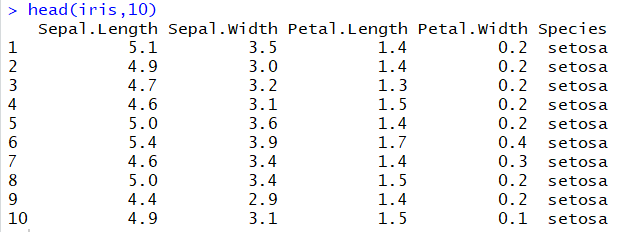
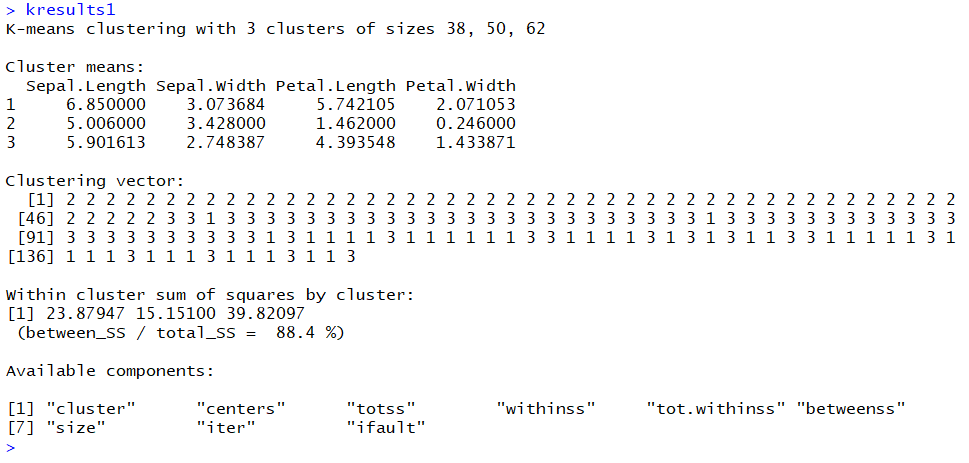
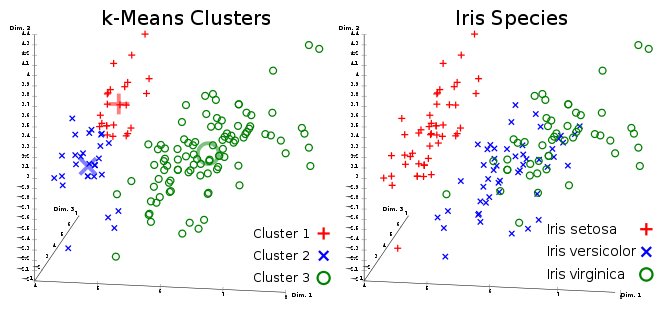
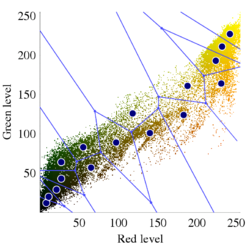
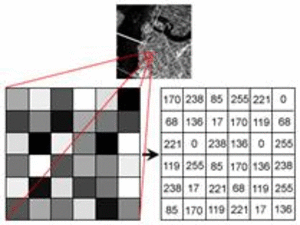
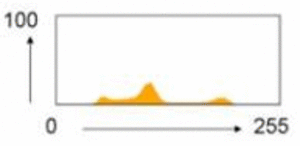
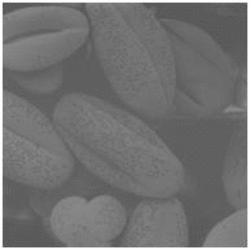
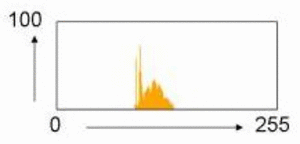
![خوشهبندی k-میانگین روشها و الگوریتمهای متعددی برای تبدیل اشیاء به گروههای همشکل یا مشابه وجود دارد. الگوریتم k-میانگین یکی از سادهترین و محبوبترین الگوریتمهایی است که در «دادهکاوی» (Data Mining) بخصوص در حوزه «یادگیری نظارت نشده» (Unsupervised Learning) به کار میرود. معمولا در حالت چند متغیره، باید از ویژگیهای مختلف اشیا به منظور طبقهبندی و خوشه کردن آنها استفاده کرد. به این ترتیب با دادههای چند بعدی سروکار داریم که معمولا به هر بعد از آن، ویژگی یا خصوصیت گفته میشود. با توجه به این موضوع، استفاده از توابع فاصله مختلف در این جا مطرح میشود. ممکن است بعضی از ویژگیهای اشیا کمی و بعضی دیگر کیفی باشند. به هر حال آنچه اهمیت دارد روشی برای اندازهگیری میزان شباهت یا عدم شباهت بین اشیاء است که باید در روشهای خوشهبندی لحاظ شود. الگوریتم خوشهبندی k-میانگین از گروه روشهای خوشهبندی تفکیکی (Partitioning Clustering) محسوب میشود و درجه پیچیدگی محاسباتی آن برابر با O ( n d k + 1 ) است، به شرطی که n تعداد اشیاء، d بعد ویژگیها و k تعداد خوشهها باشد. همچنین پیچیدگی زمانی برای این الگوریتم برابر با O ( n k d i ) است، که البته منظور از i تعداد تکرارهای الگوریتم برای رسیدن به جواب بهینه است. در خوشهبندی k-میانگین از بهینهسازی یک تابع هدف (Object Function) استفاده میشود. پاسخهای حاصل از خوشهبندی در این روش، ممکن است به کمک کمینهسازی (Minimization) یا بیشینهسازی (Maximization) تابع هدف صورت گیرد. به این معنی که اگر ملاک «میزان فاصله» (Distance Measure) بین اشیاء باشد، تابع هدف براساس کمینهسازی خواهد بود پاسخ عملیات خوشهبندی، پیدا کردن خوشههایی است که فاصله بین اشیاء هر خوشه کمینه باشد. در مقابل، اگر از تابع مشابهت (Dissimilarity Function) برای اندازهگیری مشابهت اشیاء استفاده شود، تابع هدف را طوری انتخاب میکنند که پاسخ خوشهبندی مقدار آن را در هر خوشه بیشینه کند. معمولا زمانی که هدف کمینهسازی باشد، تابع هدف را «تابع هزینه» (Cost Function) نیز مینامند. روش خوشه بندی k-میانگین، توسط «مککوئین» (McQueen) جامعه شناس و ریاضیدان در سال ۱۹۶۵ ابداع و توسط دیگر دانشمندان توسعه و بهینه شد. برای مثال در سال 1957 نسخه دیگری از این الگوریتم به عنوان الگوریتم استاندارد خوشهبندی k-میانگین، توسط «لوید» (Lloyd) در آزمایشگاههای بل (Bell Labs) برای کدگذاری پالسها ایجاد شد که بعدها در سال 1982 منتشر گردید. این نسخه از الگوریتم خوشهبندی، امروزه در بیشتر نرمافزارهای رایانهای که عمل خوشهبندی k-میانگین را انجام میدهند به صورت استاندارد اجرا میشود. در سال 1956 «فورجی» (W.Forgy) به طور مستقل همین روش را ارائه کرد و به همین علت گاهی این الگوریتم را با نام لوید-فورجی میشناسند. همچنین روش هارتیگان- ونگ (Hartigan-Wong) که در سال ۱۹۷۹ معرفی شد یکی از روشهایی است که در تحقیقات و بررسیهای دادهکاوی مورد استفاده قرار میگیرد. تفاوت در این الگوریتمها در مرحله آغازین و شرط همگرایی الگوریتمها است ولی در بقیه مراحل و محاسبات مانند یکدیگر عمل میکنند. به همین علت همگی را الگوریتمهای خوشهبندی k-میانگین مینامند. روش خوشهبندی k-میانگین فرض کنید مشاهدات ( x 1 , x 2 , … , x n ) که دارای d بعد هستند را باید به k بخش یا خوشه تقسیم کنیم. این بخشها یا خوشهها را با مجموعهای به نام S = { S 1 , S 2 , … , S k } میشناسیم. اعضای خوشهها باید به شکلی از مشاهدات انتخاب شوند که تابع «مجموع مربعات درون خوشهها» (within-cluster sum of squares- WCSS) که در حالت یک بعدی شبیه واریانس است، کمینه شود. بنابراین، تابع هدف در این الگوریتم به صورت زیر نوشته میشود. a r g m i n S k ∑ i = 1 ∑ x ∈ S i ∥ x − μ i ∥ 2 = a r g m i n S k ∑ i = 1 | S i | Var S i در اینجا منظور از μ i میانگین خوشه S i و | S i | تعداد اعضای خوشه iام است. البته میتوان نشان داد که کمینه کردن این مقدار به معنی بیشینهسازی میانگین مربعات فاصله بین نقاط در خوشههای مختلف (between-Cluster sum of Squares- BCSS) است زیرا طبق قانون واریانس کل، با کم شدن مقدار WCSS، مقدار BCSS افزایش مییابد، زیرا واریانس کل ثابت است. در ادامه به بررسی روش خوشه بندی k-میانگین به روش لوید-فورجی (استاندارد) و هارتیگان-ونگ میپردازیم. خوشهبندی k-میانگین با الگوریتم لوید (Lloyd’s Algorithm) به عنوان یک الگوریتم استاندارد برای خوشهبندی k-میانگین از الگوریتم لوید بخصوص در زمینه علوم کامپیوتر، استفاده میشود. ابتدا به علائمی که در این رابطه به کار میرود، اشاره میکنیم. m ( i ) j : میانگین مقدارهای مربوط به خوشه jام در تکرار iام از الگوریتم را با این نماد نشان میدهیم. S ( i ) j : مجموعه اعضای خوشه jام در تکرار iام الگوریتم. الگوریتم لوید را با توجه به نمادهای بالا میتوان به دو بخش تفکیک کرد. ۱- بخش مقدار دهی ( A s s i g n m e n t S t e p )، ۲- بخش به روز رسانی (Update Step). حال به بررسی مراحل اجرای این الگوریتم میپردازیم. در اینجا فرض بر این است که نقاط مرکزی اولیه یعنی m ( 1 ) 1 , m ( 1 ) 2 , ⋯ , m ( 1 ) k داده شدهاند. بخش مقدار دهی: هر مشاهده یا شی را به نزدیکترین خوشه نسبت میدهیم. به این معنی که فاصله اقلیدسی هر مشاهده از مراکز، اندازه گرفته شده سپس آن مشاهده عضو خوشهای خواهد شد که کمترین فاصله اقلیدسی را با مرکز آن خوشه دارد. این قانون را به زبان ریاضی به صورت S ( t ) i = { x p : ∥ ∥ x p − m ( t ) i ∥ ∥ 2 ≤ ∥ ∥ x p − m ( t ) j ∥ ∥ 2 ∀ j , 1 ≤ j ≤ k } مینویسیم. بخش به روز رسانی: میانگین خوشههای جدید محاسبه میشود. در این حالت داریم: m ( t + 1 ) i = 1 | S ( t ) i | ∑ x j ∈ S ( t ) i x j توجه داشته باشید که منظور از | S ( t ) i | تعداد اعضای خوشه iام است. الگوریتم زمانی متوقف میشود که مقدار برچسب عضویت مشاهدات تغییری نکند. البته در چنین حالتی هیچ تضمینی برای رسیدن به جواب بهینه (با کمترین مقدار برای تابع هزینه) وجود ندارد. کاملا مشخص است که در رابطه بالا، فاصله اقلیدسی بین هر نقطه و مرکز خوشه ملاک قرار گرفته است. از این جهت از میانگین و فاصله اقلیدسی استفاده شده که مجموع فاصله اقلیدسی نقاط از میانگینشان کمترین مقدار ممکن نسبت به هر نقطه دیگر است. نکته: ممکن است فاصله اقلیدسی یک مشاهده از دو مرکز یا بیشتر، برابر باشد ولی در این حالت آن شئ فقط به یکی از این خوشهها تعلق خواهد گرفت. تصویر زیر یک مثال برای همگرایی الگوریتم لوید محسوب میشود که مراحل اجرا در آن دیده میشود. همانطور که مشخص است الگوریتم با طی ۱۴ مرحله به همگرایی میرسد و دیگر میانگین خوشهها تغییری نمییابد. البته ممکن است که این نقاط نتیجه تابع هزینه را بطور کلی (Global) کمینه نکنند زیرا روش k-میانگین بهینهسازی محلی (Local Optimization) را به کمک مشتقگیری و محاسبه نقاط اکستریمم اجرا میکند. K-means_convergence همگرایی الگوریتم k-میانگین نکته: به نقاط مرکزی هر خوشه مرکز (Centroid) گفته میشود. ممکن است این نقطه یکی از مشاهدات یا غیر از آنها باشد. مشخص است که در الگوریتم لوید، k مشاهده به عنوان مرکز خوشهها (Centroids) در مرحله اول انتخاب شدهاند ولی در مراحل بعدی، مقدار میانگین هر خوشه نقش مرکز را بازی میکند. خوشهبندی k-میانگین با الگوریتم هارتیگان-ونگ (Hartigan-Wong) یکی از روشهای پیشرفته و البته با هزینه محاسباتی زیاد در خوشهبندی k-میانگین، الگوریتم هارتیگان-ونگ است. برای آشنایی با این الگوریتم بهتر است ابتدا در مورد نمادهایی که در ادامه خواهید دید توضیحی ارائه شود. ϕ ( S j ) : از این نماد برای نمایش «تابع هزینه» برای خوشه S j استفاده میکنیم. این تابع در خوشهبندی k-میانگین برابر است با: ϕ ( S i ) = ∑ x ∈ S j ( x − μ j ) 2 S j : از آنجایی که هدف از این الگوریتم، تفکیک اشیاء به k گروه مختلف است، گروهها یا خوشهها در مجموعهای با نام S قرار دارند و داریم، S = { S 1 , S 2 , ⋯ , S k } . μ j : برای نمایش میانگین خوشهjام از این نماد استفاده میشود. بنابراین خواهیم داشت: μ j = ∑ x ∈ S j x n j n j : این نماد تعداد اعضای خوشه jام را نشان میدهد. بطوری که j = { 1 , 2 , ⋯ , k } است. البته مشخص است که در اینجا تعداد خوشهها را با k نشان دادهایم. مراحل اجرای الگوریتم در خوشهبندی k-میانگین با الگوریتم هارتیگان میتوان مراحل اجرا را به سه بخش تقسیم کرد: ۱- بخش مقدار دهی اولیه ( A s s i g n m e n t S t e p ) ، ۲- بخش به روز رسانی ( U p d a t e S t e p )، ۳- بخش نهایی (Termination). در ادامه به بررسی این بخشها پرداخته میشود. بخش مقدار دهی اولیه: در الگوریتم هارتیگان-ونگ، ابتدا مشاهدات و یا اشیاء به طور تصادفی به k گروه یا خوشه تقسیم میشوند. به این کار مجموعه S با اعضایی به صورت { S j } j ∈ { i , ⋯ , k } مشخص میشود. بخش به روز رسانی: فرض کنید که مقدارهای n و m از اعداد ۱ تا k انتخاب شده باشد. مشاهده یا شیئ از خوشه nام را در نظر بگیرید که تابع Δ ( m , n , x ) = ϕ ( S n ) + ϕ ( S m ) − Φ ( S n ∖ { x } ) − ϕ ( S m ∪ { x } ) را کمینه سازد، در چنین حالتی مقدار x از خوشه nام به خوشه mام منتقل میشود. به این ترتیب شی مورد نظر در S m قرار گرفته و خواهیم داشت x ∈ S m . بخش نهایی: زمانی که به ازای همه n,m,x مقدار Δ ( m , n , x ) بزرگتر از صفر باشد، الگوریتم خاتمه مییابد. نکته: منظور از نماد ϕ ( S n ∖ { x } ) محاسبه تابع هزینه در زمانی است که مشاهده x از مجموعه S n خارج شده باشد. همچنین نماد ϕ ( S m ∪ { x } ) به معنی محاسبه تابع هزینه در زمانی است که مشاهده x به خوشه S m اضافه شده باشد. در تصویر زیر مراحل اجرای الگوریتم هارتیگان به خوبی نمایش داده شده است. هر تصویر بیانگر یک مرحله از اجرای الگوریتم است. نقاط رنگی نمایش داده شده، همان مشاهدات هستند. هر رنگ نیز بیانگر یک خوشه است. در تصویر اول مشخص است که در بخش اول از الگوریتم به طور تصادفی خوشهبندی صورت پذیرفته. ولی در مراحل بعدی خوشهها اصلاح شده و در انتها به نظر میرسد که بهترین تفکیک برای مشاهدات رسیدهایم. در تصویر آخر نیز مشخص است که مراکز خوشهها، محاسبه و ثابت شده و دیگر بهینهسازی صورت نخواهد گرفت. به این ترتیب پاسخهای الگوریتم با طی تکرار ۵ مرحله به همگرایی میرسد. hartigan algorithm الگوریتم هارتیگان بخش مقدار دهی اولیه hartigan algorithm الگوریتم هارتیگان تکرار ۱ hartigan algorithm الگوریتم هارتیگان تکرار ۲ hartigan algorithm الگوریتم هارتیگان تکرار ۳ hartigan algorithm الگوریتم هارتیگان تکرار ۴ hartigan algorithm الگورییتم هارتیگان تکرار ۵ اجرای این الگوریتمها با استفاده از دستورات زبان برنامهنویسی R برای استفاده از دستورات و فرمانهای مربوط به خوشهبندی k-میانگین، باید بسته یا Package مربوط به خوشهبندی kmeans به اسم stats را در R نصب کرده باشد. البته از آنجایی این بسته بسیار پرکاربرد است، معمولا به طور خودکار فراخوانی شده است. کدهای زیر نشانگر استفاده از الگوریتم خوشهبندی توسط روشهای مختلف آن است. library(stats) data=iris[,1:4] method=c("Hartigan-Wong", "Lloyd", "MacQueen") k=3 kresults1=kmeans(data,k,algorithm = method[1]) kresults2=kmeans(data,k,algorithm=method[2]) kresults3=kmeans(data,k,algorithm=method[3]) kresults1 kresults2 kresults3 1 2 3 4 5 6 7 8 9 10 11 12 library(stats) data=iris[,1:4] method=c("Hartigan-Wong", "Lloyd", "MacQueen") k=3 kresults1=kmeans(data,k,algorithm = method[1]) kresults2=kmeans(data,k,algorithm=method[2]) kresults3=kmeans(data,k,algorithm=method[3]) kresults1 kresults2 kresults3 با توجه به دادههای iris که مربوط به اندازه و ابعاد کاسبرگ و گلبرگ سه نوع گل مختلف است، خوشهبندی به سه دسته انجام شده است. اطلاعات مربوط به ۱۰ سطر اول این مجموعه داده، به صورت زیر است. با اجرای کدهای نوشته شده، خوشهبندی انجام شده و نتابج تولید میشوند. به عنوان مثال میتوان خروجی را برای kresult1 که انجام خوشه بندی توسط الگوریتم هارتیگان است به صورت زیر مشاهده کرد: iris clustering همانطور که دیده میشود، در سطر اول تعداد اعضای هر خوشه، نمایش داده شده است. در بخش دوم که با سطر ۱ و ۲ و ۳ مشخص شده، مراکز هر سه خوشه برحسب ویژگیهای (طول و عرض کاسبرگ و طول و عرض گلبرگ) محاسبه شده و در قسمت Cluster Vector نیز برچسب خوشه هر کدام از مشاهدات دیده میشود. در انتها نیز مجموع مربعات فاصله درون خوشهای (مجموع فاصله هر مشاهده از مرکز خوشه) استخراج شده و درصد یا شاخص ارزیابی خوشهبندی بر اساس نسبت مربعات بین خوشهها به مربعات کل دیده میشود. این مقدار برای این حالت برابر ۸۸.۴٪ است که نشان میدهد بیشتر پراکندگی (total_ss) توسط پراکندگی بین خوشهها (between_ss) بیان شده است. پس به نظر خوشهبندی مناسب خواهد بود. پس اختلاف بین گروهها ناشی از خوشههای است که مشاهدات را به دستههای جداگانه تفکیک کرده. همچنین در کدها مشخص است که تعداد خوشههای در متغیر k ثبت و به کار رفته است. در شکل دیگری از دستور kmeans میتوان به جای معرفی تعداد خوشهها از مراکز دلخواه که با تعداد خوشهها مطابقت دارد، استفاده کرد. برای مثال اگر برنامه به صورت زیر نوشته شود، الگوریتم ابتدا نقاط معرفی شده را به عنوان نقاط مرکزی (Centroids) به کار گرفته و سپس مراحل بهینه سازی را دنبال میکند. از آنجا که سه نقطه مبنا قرار گرفته، الگوریتم متوجه میشود که باید مشاهدات به سه خوشه تفکیک شود. library(stats) data=iris[,1:4] method=c("Hartigan-Wong", "Lloyd", "MacQueen") c1=c(6,4,5,3) c2=c(5,3,1,0) c3=c(6,2,4,2) centers=rbind(c1,c2,c3) kresults1=kmeans(x = data,centers = centers,algorithm = method[1]) kresults2=kmeans(x = data,centers = centers,algorithm=method[2]) kresults3=kmeans(x = data,centers = centers,algorithm=method[3]) kresults1 kresults2 kresults3 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 library(stats) data=iris[,1:4] method=c("Hartigan-Wong", "Lloyd", "MacQueen") c1=c(6,4,5,3) c2=c(5,3,1,0) c3=c(6,2,4,2) centers=rbind(c1,c2,c3) kresults1=kmeans(x = data,centers = centers,algorithm = method[1]) kresults2=kmeans(x = data,centers = centers,algorithm=method[2]) kresults3=kmeans(x = data,centers = centers,algorithm=method[3]) kresults1 kresults2 kresults3 در تصویر زیر نتیجه خوشه بندی k-میانگین را برای دادههای iris توسط یک نمودار مشاهده میکنید. البته باید توجه داشت که این نمودار دو بعدی است در حالیکه دادهها، دارای چهار ویژگی هستند. به کمک روشهای آماری مانند تجزیه به مولفههای اصلی (PCA) ابعاد مسئله کاهش یافته تا در سه بعد روی نمودار نمایش داده شود. سمت راست تصویر گروههای واقعی و سمت چپ نتیجه خوشهبندی دیده میشود. نقاطی که در خوشهها به درستی تشخیص داده نشدهاند، باعث افزایش خطای خوشهبندی خواهند شد. کاربردها از الگوریتم خوشهبندی k-میانگین در «بخشبندی بازار کسب و کار» (market Segmentation)، «دستهبندی مشتریان» (Customer Segmentation)، «بینایی رایانهای» (Computer Vision) و «زمینآمار (Geostatistics) استفاده می شود. برای مثال در تشخیص تعداد رنگ و یا فشرده سازی تصاویر برحسب رنگها میتوان از این الگوریتمها استفاده کرد. در تصویر بالا گل رز زرد رنگی دیده میشود که در یک محیط سبز قرار گرفته است. با استفاده از الگوریتمهای خوشهبندی میتوان تعداد رنگها را کاهش داده و از حجم تصاویر کاست. در تصویر زیر دسته بندی رنگهای گل رز دیده میشود. در این تصویر، هر طیف رنگ براساس میزان رنگ قرمز و سبز، بوسیله «سلولهای ورونوی» (Voronoi Cell) تقسیمبندی شده است. این تقسیمبندی میتواند توسط الگوریتمها خوشهبندی k-میانگین صورت گرفته باشد. در کل تصویر نیز، طیف رنگهای مختلف برای تصویر گل رز در یک «نمودار ورونوی» (Voronoi diagram) نمایش داده شده است که خوشهها را بیان میکند. معایب و مزایای خوشهبندی k-میانگین از آنجایی که در این روش خوشهبندی، محاسبه فاصله بین نقاط توسط تابع فاصله اقلیدسی انجام میشود، از این الگوریتمها به صورت استاندارد، فقط برای مقدارهای عددی (و نه ویژگیهای کیفی) میتوان استفاده کرد. از طرف دیگر با توجه به محاسبات ساده و سریع آنها، پرکاربرد و موثر است. از طرف دیگر نسخههای تعمیم یافته از روش خوشه بندی k-میانگین نیز وجود دارد که با توابع فاصله دیگر مانند فاصله منهتن و یا فاصلههایی که برای دادههای باینری قابل استفاده است، مراحل خوشهبندی را انجام میدهد. به منظور ارزیابی نتایج خوشهبندی از معیارهای متفاوتی کمک گرفته میشود. ممکن است از قبل برچسب خوشهها مشخص باشد و بخواهیم کارایی الگوریتم را با توجه به مقایسه برچسبهای واقعی و حاصل از خوشهبندی، اندازهگیری کنیم. در این حالت، شاخصهای ارزیابی بیرونی، بهترین راهنما و معیار برای سنجش صحت نتایج خوشهبندی محسوب میشوند. معمولا به این برچسبها، استاندارد طلایی (Golden Standard) و در کل چنین عملی را ارزیابی Benchmark میگویند. برای مثال شاخص رَند (Rand Index) یکی از این معیارها و شاخصهای بیرونی است که از محبوبیت خاصی نیز برخوردار است. از طرف دیگر اگر هیچ اطلاعات اولیه از ساختار و دستهبندی مشاهدات وجود نداشته باشد، فقط ملاک ارزیابی، میتواند اندازههایی باشد که میزان شباهت درون خوشهها و یا عدم شباهت یا فاصله بین خوشهها را اندازه میگیرند. بنابراین برای انتخاب بهتر و موثرترین روش خوشهبندی از میزان شباهت درون خوشهها و شباهت بین خوشهها استفاده میشود. روشی که دارای میزان شباهت بین خوشهای کم و شباهت درون خوشهای زیاد باشد مناسبترین روش خواهد بود. این معیارها را به نام شاخصهای ارزیابی درونی میشناسیم. به عنوان مثال شاخص نیمرخ (silhouette) یکی از این معیارها است که شاخصی برای سنجش مناسب بودن تعلق هر مشاهده به خوشهاش ارائه میدهد. به این ترتیب معیاری برای اندازهگیری کارایی الگوریتم خوشهبندی بدست میآید. اگر این مطلب برایتان مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند: مجموعه آموزشهای یادگیری ماشین و بازشناسی الگو مجموعه آموزشهای آمار، احتمالات و دادهکاوی آموزش خوشه بندی K میانگین (K-Means) با نرم افزار SPSS آموزش خوشه بندی تفکیکی با نرم افزار R آموزش خوشه بندی سلسله مراتبی با SPSS آشنایی با خوشهبندی (Clustering) و شیوههای مختلف آن روش های ارزیابی نتایج خوشه بندی (Clustering Performance) — معیارهای درونی (Internal Index) روش های ارزیابی نتایج خوشه بندی (Clustering Performance) — معیارهای بیرونی (External Index) ^^ telegram twitter به اشتراک بگذارید: منبع وبلاگ فرادرسWikipedia بر اساس رای 1 نفر آیا این مطلب برای شما مفید بود؟ بلیخیر نظر شما چیست؟ نشانی ایمیل شما منتشر نخواهد شد. بخشهای موردنیاز علامتگذاری شدهاند * متن نظر * نام شما * ایمیل شما * پایتخت ایران کدام شهر است؟ برچسبها clusterClusteringclustering algorithmcost functiondata miningforgy algorithmhartigan-wong algorithmk-meanslloyd algorithmmaximizationMcQueen algorithmminimizationpartitioning algorithmunsupervise learningتابع هدفتابع هزینهتعداد خوشهخوشه بندیخوشه بندی K میانگینخوشه بندی در آمارخوشهبندیخوشهبندی k-میانگینمربعات بین خوشهمربعات درون خوشهمعیارهای ارزیابی خوشه عضویت در خبرنامه ایمیل * آموزش برنامه نویسی آموزش متلب Matlab نرمافزارهای مهندسی برق نرمافزارهای مهندسی عمران نرمافزارهای مهندسی مکانیک نرمافزارهای مهندسی صنایع](https://blog.faradars.org/wp-content/uploads/2018/10/kmeans.jpg)