بایگانی‌های sgsgi lvhjfd

بایگانی برچسب برای: sgsgi lvhjfd

خوشه بندی (Clustering) قسمت 4

خوشه‌بندی سلسله مراتبی (Hierarchical Clustering)

برعکس خوشه‌بندی تفکیکی که اشیاء را در گروه‌های مجزا تقسیم می‌کند، «خوشه‌بندی سلسله مراتبی» (Hierarchical Clustering)، در هر سطح از فاصله، نتیجه خوشه‌بندی را نشان می‌دهد. این سطوح به صورت سلسله مراتبی (Hierarchy) هستند.

برای نمایش نتایج خوشه‌بندی به صورت سلسله مراتبی از «درختواره» (Dendrogram) استفاده می‌شود. این شیوه، روشی موثر برای نمایش نتایج خوشه‌بندی سلسله مراتبی است. در تصویر ۲ نتایج خوشه‌بندی سلسله مراتبی روی داده‌های $s = 1, 3, 6, 2, 8, 10$ با استفاده از درختواره را می‌بینید.

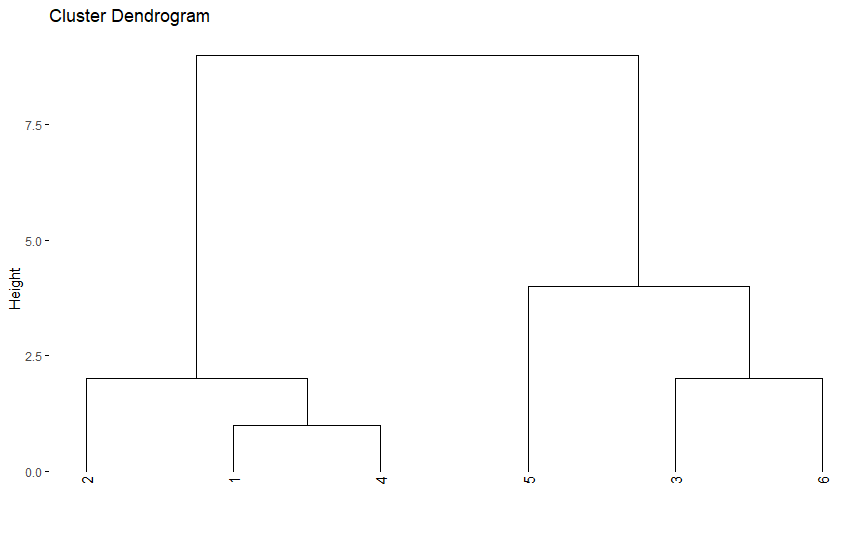
تصویر ۲- نمودار دختواره برای داده‌های مربوط s=1,3,6,2,8,10

همانطور که در تصویر ۲ قابل رویت است،‌ ابتدا هر مقدار یک خوشه محسوب می‌شود. در طی مراحل خوشه‌بندی، نزدیکترین مقدارها (براساس تابع فاصله تعریف شده) با یکدیگر ادغام شده و خوشه جدیدی می‌سازند.

در نتیجه براساس تصویر ۲ ابتدا در مرحله اول مقدار اول و چهارم تشکیل اولین خوشه را می‌دهند، زیرا کمترین فاصله را دارند. سپس در مرحله دو، مقدار دوم با خوشه تشکیل شده در مرحله اول ترکیب می‌شود. در مرحله سوم مقدارهای سوم و ششم با هم تشکیل یک خوشه می‌دهند که در مرحله چهارم با مقدار پنجم ترکیب شده و خوشه جدیدی می‌سازند.

در انتها نیز خوشه تشکیل شده در مرحله دوم با خوشه تشکیل شده در مرحله چهارم ادغام شده و خوشه نهایی را ایجاد می‌کنند. همانطور که دیده می‌شود با داشتن شش مقدار خوشه‌بندی سلسله مراتبی، پنچ مرحله خواهد داشت زیرا در هر مرحله فقط یک عمل ادغام انجام می‌شود.

نکته: توجه داشته باشید که مقدارهایی که روی محور افقی دیده می‌شوند، بیانگر موقعیت مقدارها در لیست داده‌ها است و نه خود مقادیر. همچنین محور عمودی نیز فاصله یا ارتفاع بین خوشه‌ها را نشان می‌دهد.

در الگوریتم خوشه‌بندی سلسله مراتبی معمولا با کوچکترین خوشه‌ها شروع می‌کنیم. به این معنی که در ابتدا هر مقدار بیانگر یک خوشه است. سپس دو مقداری که بیشترین شباهت (کمترین فاصله) را دارند با یکدیگر ادغام شده و یک خوشه جدید می‌سازند. بعد از این مرحله، ممکن است دو مقدار یا یک مقدار با یک خوشه یا حتی دو خوشه با یکدیگر ادغام شده و خوشه جدیدی ایجاد کنند.

این عملیات با رسیدن به بزرگترین خوشه که از همه مقدارها تشکیل یافته پایان می‌یابد. به این ترتیب اگر n مقدار داشته باشیم در مرحله اول تعداد خوشه‌ها برابر با n‌ است و در آخرین مرحله یک خوشه باقی خواهد ماند.

برای اندازه‌گیری فاصله بین دو خوشه یا یک مقدار با یک خوشه از روش‌های «پیوند» (Linkage) استفاده می‌شود. از انواع روش‌های پیوند می‌توان به «نزدیکترین همسایه» (Nearest Neighbor) یا «پیوند تکی» (Single Linkage)، «دورترین همسایه» (Furthest Neighbor) یا «پیوند کامل» (Complete Linkage) و همچنین «پیوند میانگین» (Average Linkage) اشاره کرد.

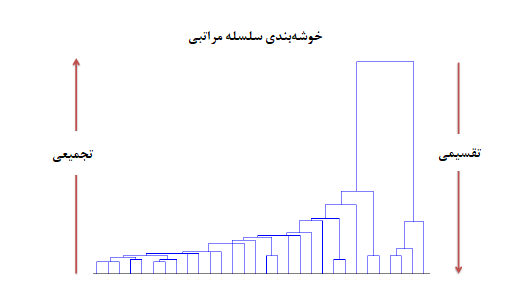
معمولا به این شیوه خوشه‌بندی سلسله مراتبی، روش «تجمیعی» (Agglomerative) می‌گویند.

برعکس اگر عمل خوشه‌بندی سلسله مراتبی به شکلی باشد که با بزرگترین خوشه، عملیات خوشه‌بندی شروع شده و با تقسیم هر خوشه به خوشه‌های کوچکتر ادامه پیدا کند، به آن «خوشه‌بندی سلسله مراتبی تقسیمی» (Divisive Hierarchical Clustering) می‌گویند. در آخرین مرحله این روش، هر مقدار تشکیل یک خوشه را می‌دهد پس n خوشه خواهیم داشت.

هر چند شیوه نمایش خوشه‌بندی سلسله مراتبی تقسیمی نیز توسط درختواره انجام می‌شود ولی از آنجایی که محدودیت‌هایی برای تقسیم یک خوشه به زیر خوشه‌های دیگر وجود دارد، روش تقسیمی کمتر به کار می‌رود.

نکته: در شیوه خوشه‌بندی سلسله مراتبی، عمل برچسب گذاری در طی مراحل خوشه‌بندی اصلاح پذیر نیست. به این معنی که وقتی عضوی درون یک خوشه قرار گرفت هرگز از آن خوشه خارج نمی‌شود.

از الگوریتم‌های معروف برای خوشه‌بندی سلسله مراتبی تجمیعی می‌توان به AGNES و برای تقسیمی به DIANA اشاره کرد.

خوشه‌بندی برمبنای چگالی (Density-Bases Clustering)

روش‌های خوشه‌بندی تفکیکی قادر به تشخیص خوشه‌هایی کروی شکل هستند. به این معنی که برای تشخیص خوشه‌ها از مجموعه داده‌هایی به شکل‌های «کوژ» (Convex) یا محدب خوب عمل می‌کنند. در عوض برای تشخیص خوشه‌ها برای مجموعه داده‌های «کاو» (Concave) یا مقعر دچار خطا می‌شوند. به تصویر ۳ توجه کنید که بیانگر شکل‌های کاو است.

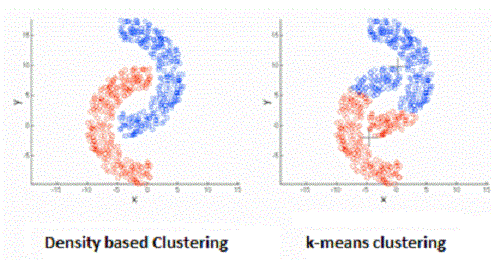
تصویر ۳- مقایسه نتایج خوشه‌بندی تفکیکی با روش چگالی

همانطور که دیده می‌شود میانگین هر دو خوشه در روش k-means در محلی قرار گرفته است که مربوط به خوشه‌ دیگر است. در حالی که خوشه‌بندی برمبنای چگالی به خوبی نقاط را در خوشه‌های درست قرار داده است.

در الگوریتم‌ها خوشه‌بندی برمبنای چگالی، نقاط با تراکم زیاد شناسایی شده و در یک خوشه قرار می‌گیرند. از الگوریتم‌های معروف در این زمینه می‌توان به DBSCAN اشاره کرد که در سال ۱۹۹۶ توسط «استر» (Ester) معرفی شد.

این الگوریتم توانایی شناسایی نقاط دورافتاده را داشته و می‌تواند تاثیر آن‌ها را در نتایج خوشه‌بندی از بین ببرد. شیوه کارکرد این الگوریتم‌ بنا به تعریف‌های زیر قابل درک است:

همسایگی به شعاع : اگر فضای با شعاع $ϵ$ را حول نقطه‌ای x در نظر بگیریم، یک همسایگی ایجاد کرده‌ایم که به شکل $N_{ϵ} (x)$ نشان داده می‌شود. شکل ریاضی این همسایگی به صورت زیر است.

$N_{ϵ} (x) = {y \in D; d (x, y) \leq ϵ}$

بطوری که D مجموعه داده و d تابع فاصله است. تصویر 4 مفهوم همسایگی را نشان می‌دهد.

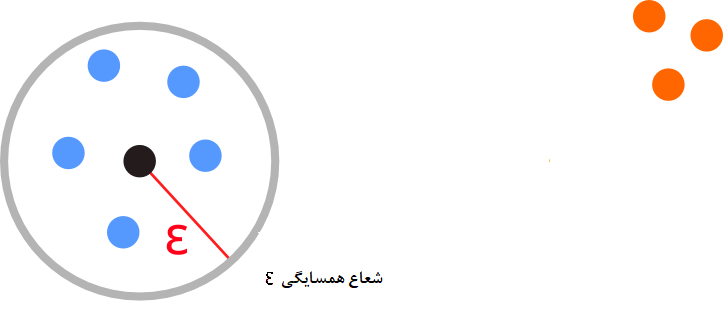
تصویر ۴- همسایگی و شعاع همسایگی

قابل دسترسی مستقیم (Directly density-reachable): نقطه x را قابل دسترسی مستقیم از y می‌نامند اگر براساس دو پارامتر $N_{m i n}$ و $ϵ$ داشته باشیم:

$x \in N_{ϵ} (y)$

$| N_{ϵ} (y) | \geq N_{m i n}$

در اینجا $| N_{ϵ} (y)$ نشانگر تعداد اعضای همسایگی به شعاع $ϵ$ از نقطه y است.

پس شرط اول به معنی این است که x در همسایگی از y قرار دارد و شرط دوم نیز بیان می‌کند که باید تعداد اعضای همسایگی y از حداقل تعداد اعضای همسایگی بیشتر باشد.

نقطه قابل دسترسی (Density-Reachable): نقطه x را از طرق y‌ نامیده می‌شود، اگر دنباله‌ای از نقاط مثل $x_{1}, x_{2}, \dots, x_{i}$ موجود باشند که نقطه x را به y برسانند. یعنی:

$x = x_{1}, x_{2}, \dots, x_{i} = y$

در این حالت برای مثال $x_{1}$ «قابل دسترسی مستقیم» (Direct Reachable) به $x_{2}$ ‌ نامیده می‌شود.

نقاط متصل (Density-Connected): دو نقطه x و y را متصل گویند اگر براساس پارامترهای $ϵ$ و $N_{m i n}$ نقطه‌ای مانند z وجود داشته باشد که هر دو نقطه x و y از طریق آن قابل دسترسی باشند.
خوشه (Cluster): فرض کنید مجموعه داده D موجود باشد. همچنین C یک زیر مجموعه غیر تهی از D‌ باشد. C را یک خوشه می‌نامند اگر براساس پارمترهای $ϵ$ و $N_{m i n}$ در شرایط زیر صدق کند:

۱- اگر x درون C باشد و y نیز قابل دسترسی به x با پارامترهای $ϵ$ و $N_{m i n}$ باشد، آنگاه y نیز در C‌ است.

۲- اگر دو نقطه x و y در C باشند آنگاه این نقاط براساس پارامترهای $ϵ$ و $N_{m i n}$ نقاط متصل محسوب شوند.

به این ترتیب خوشه‌ها شکل گرفته و براساس میزان تراکمشان تشکیل می‌شوند. نویز یا نوفه (Noise) نیز نقاطی خواهند بود که در هیچ خوشه‌ای جای نگیرند. برای روشن شدن این تعریف‌ها به تصویر 5 توجه کنید.

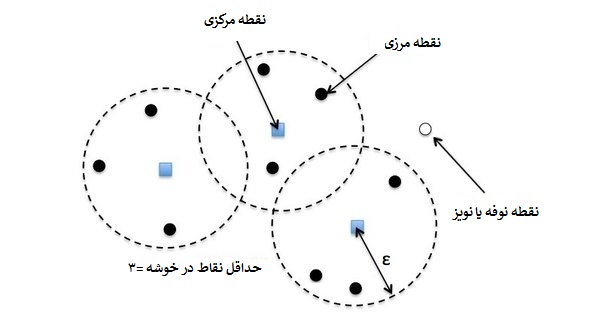
تصویر ۵- نقاط مرکزی، مرزی، نوفه (نویز)

نکته: با توجه به تعریف خوشه، مشخص است که اندازه هر خوشه از $N_{m i n}$ بیشتر است.

مراحل خوشه‌بندی برمبنای چگالی به این ترتیب است که ابتدا یک نقطه را به صورت اختیاری انتخاب کرده و نقاط قابل دسترس برای آن پیدا می‌شود. اگر x یک نقطه مرکزی باشد (نقطه‌ای که درون خوشه قرار داشته باشد)، خوشه را تشکیل می‌دهد ولی اگر x نقطه‌ای مرزی باشد (نقطه‌ای که در لبه‌های خوشه قرار داشته باشد) آنگاه هیچ نقطه‌ قابل دسترسی برای x وجود نخواهد داشت و الگوریتم از نقطه‌ای دیگری ادامه پیدا می‌کند.

در مراحل خوشه‌بندی ممکن است دو خوشه که به یکدیگر نزدیک باشند، ادغام شوند. فاصله بین دو خوشه برحسب حداقل فاصله بین اعضای دو خوشه (پیوند تکی) سنجیده می‌شود.

نکته: انتخاب مقدار برای پارامترهای $ϵ$ و $N_{m i n}$ مسئله مهمی است که براساس نظر محقق باید به الگوریتم داده شوند. ترسیم نمودار داده‌ها در انتخاب این پارامترها می‌تواند موثر باشد. هرچه داده‌ها در دسته‌های متراکم‌تر دیده شوند بهتر است مقدار $ϵ$ را کوچک در نظر گرفت و اگر لازم است که تعداد خوشه‌ها کم باشند بهتر است مقدار $N_{m i n}$ را بزرگ انتخاب کرد.

خوشه‌بندی برمبنای مدل (Model-Based Clustering)

در روش‌های پیشین، فرضیاتی مبنی بر وجود یک توزیع آماری برای داده‌ها وجود نداشت. در روش «خوشه‌بندی برمبنای مدل» (Model-Based Clustering) یک توزیع آماری برای داده‌ها فرض می‌شود. هدف در اجرای خوشه‌بندی برمبنای مدل، برآورد پارامترهای توزیع آماری به همراه متغیر پنهانی است که به عنوان برچسب خوشه‌ها در مدل معرفی شده.

با توجه به تعداد خوشه‌هایی که در نظر گرفته شده است، مثلا k، تابع درستنمایی را برای پیدا کردن خوشه‌ها به صورت زیر می‌نویسند:

$L_{M} (Θ_{1}, Θ_{2}, Θ_{3}, \dots, Θ_{k}; t_{1}, t_{2}, \dots, t_{k}) = n \prod i = 1 k \sum j = 1 t_{j} f_{j} (x_{i}, Θ_{j})$

در رابطه بالا $t_{j}$ بیانگر احتمال تعلق نقطه به خوشه jام و $f_{j}$ نیز توزیع آمیخته با پارامترهای $Θ_{j}$ است.

در اکثر مواقع برای داده‌ها توزیع نرمال آمیخته در نظر گرفته می‌شود. در چنین حالتی توزیع آمیخته را به فرمی می‌نویسند که درصد آمیختگی (درصدی از داده‌ها که متعلق به هر توزیع هستند) نیز به عنوان پارامتر در مدل حضور دارد.

$f (x) = k \sum j = 1 p_{j} Φ (X; μ_{j}, Σ_{i})$

در رابطه بالا $Φ$ توزیع نرمال با پارامترهای $μ_{j}$ و $Σ_{j}$ برای توزیع jام هستند و $p_{j}$ ‌ نیز درصد آمیختگی برای توزیع jام محسوب می‌شود. در تصویر 6 یک نمونه از توزیع آمیخته نرمال دو متغیره نمایش داده شده است.

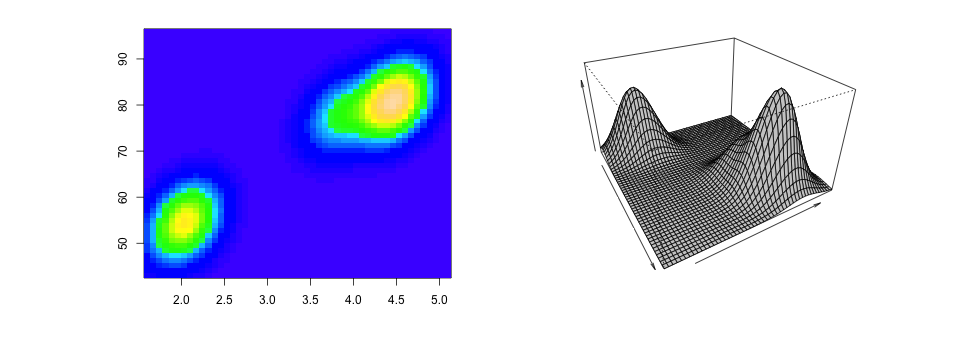
تصویر ۶- توزیع آمیخته نرمال دو متغیره

انتخاب‌های مختلفی برای ماتریس واریانس-کوواریانس یا $Σ$ وجود دارد. یکی از این حالت‌ها در نظر گرفتن استقلال و یکسان بودن واریانس برای همه توزیع‌ها است. همچنین می‌توان واریانس هر توزیع را متفاوت از توزیع‌های دیگر در نظر گرفت و بدون شرط استقلال عمل کرد. در حالت اول پیچیدگی مدل و تعداد پارامترهای برآورد شده کم و در حالت دوم پیچیدگی مدل و تعداد پارامترهای برآورده شده زیاد خواهد بود.

برای برآورد پارامترهای چنین مدلی باید از تابع درستنمایی استفاده کرد و به کمک مشتق مقدار حداکثر را برای این تابع بدست آورد. با این کار پارامترهای مدل نیز برآورد می‌شوند. ولی با توجه به پیچیدگی تابع درستنمایی می‌توان از روش‌هایی ساده‌ و سریع‌تری نیز کمک گرفت. یکی از این روش‌ها استفاده از الگوریتم EM‌ (مخفف Expectation Maximization) است. در الگوریتم EM که براساس متغیر پنهان عمل می‌کند، می‌توان به حداکثر مقدار تابع درستنمایی همراه با برآورد پارامترها دست یافت.

در چنین حالتی می‌توان برچسب تعلق هر مقدار به خوشه را به عنوان متغیر پنهان در نظر گرفت. اگر متغیر پنهان را $z_{i j}$ ‌ در نظر بگیریم مقداری برابر با ۱ دارد اگر مشاهده iام در خوشه jام باشد و در غیر اینصورت مقدار آن 0 خواهد بود.

منبع

منابع

1.https://fa.wikipedia.org

2.https://tik4.com

3.https://blog.faradars.org

خوشه بندی (Clustering) قسمت 1
خوشه بندی (Clustering) قسمت 2
خوشه بندی (Clustering) قسمت 3
خوشه بندی (Clustering) قسمت 4

دسامبر 10, 2019/0 دیدگاه /توسط hgadmin

خوشه بندی (Clustering) قسمت 1

آموزش عمومی پردازش تصویر و بینایی ماشین

در خوشه بندی، هدف تقسیم داده به گروه‌های مختلف است که با رنگ‌های مختلف در اینجا نشان داده شده‌اند.

در تجزیه و تحلیل خوشه یا خوشه بندی، گروه بندی مجموعه ای از اشیاء انجام می‌شود اینکار به این صورت است که اشیاء در یک گروه (به نام خوشه) در مقایسه با دیگر دسته‌ها (خوشه ها) مشابه تر هستند. این وظیفه اصلی داده کاوی اکتشافی است و یک روش معمول برای تجزیه و تحلیل داده‌های آماری است که در بسیاری از زمینه‌ها از جمله یادگیری ماشین، تشخیص الگو،تجزیه و تحلیل تصویر، بازیابی اطلاعات، بیوانفورماتیک، فشرده سازی داده‌ها و گرافیک کامپیوتری استفاده می‌شود.

هدف خوشه بندی

تجزیه و تحلیل خوشه ای خود یک الگوریتم خاص نیست، بلکه روند کلی است و می‌تواند توسط الگوریتم‌های مختلفی به دست آید که در درک آنچه که یک خوشه را تشکیل می دهند و نحوه کارآمدی آن‌ها را پیدا می‌کند.

اصطلاحات خوشه‌ها شامل گروه‌هایی با فاصله‌های کم بین اعضای خوشه، مناطق متراکم فضای داده، فواصل و یا توزیع‌های آماری خاص است. بنابراین خوشه بندی می‌تواند به عنوان یک مسئله بهینه سازی چند هدفه صورت گیرد. الگوریتم خوشه بندی مناسب و تنظیمات پارامتر (از جمله پارامترهایی مانند تابع فاصله مورد استفاده، آستانه تراکم یا تعداد خوشه مورد انتظار) بستگی به تنظیم مجموعه داده‌ها توسط فرد و استفاده خاص فرد از نتایج دارد. تجزیه و تحلیل خوشه ای یک روش اتوماتیک نیست، بلکه یک فرآیند تکراری از کشف دانش یا بهینه سازی چند هدفه تعاملی است که شامل آزمایش و شکست است. اغلب لازم است که داده‌های پیش پردازش شده و پارامترهای مدل اصلاح شوند تا نتیجه حاصل ، همان نتیجهٔ دلخواه باشد.

علاوه بر اصطلاحات خوشه بندی، تعدادی از اصطلاح با معانی مشابه وجود دارد، از جمله طبقه بندی خودکار، طبقه بندی عددی، روش‌شناسی و تجزیه و تحلیل توپولوژیکی. تفاوت‌های کم اغلب در نتایج استفاده می‌شود: در داده کاوی، نتیجه گروه‌ها مورد توجه هست و در طبقه بندی خودکار، قدرت تشخیصی مورد توجه است.

تجزیه و تحلیل خوشه ای در انسان‌شناسی توسط Driver و Kroeber در سال 1932 آغاز شد و در روان‌شناسی توسط زوبین در سال 1938 و رابرت تیرون در سال 1939 معرفی شد و در سال 1943 برای طبقه بندی نظریه رفتاری در روانشناسی شخصیت توسط Cattell استفاده شده‌است.

تعریف

مفهوم “خوشه” را دقیقا نمیتوان تعریف کرد،یکی از دلایلش این است که الگوریتم‌های خوشه بندی زیادی وجود دارد. همهٔ آن‌ها یک قسمت مشترک دارند و آن یک گروه از اشیاء داده است. با این حال، محققان از مدل‌های مختلف خوشه استفاده می‌کنند و برای هر یک از این مدل‌های خوشه، الگوریتم‌های مختلفی را می‌توان ارائه داد. مفهوم یک خوشه، همانطور که توسط الگوریتم‌های مختلف یافت می‌شود، به‌طور خاصی در خواص تفاوت دارند. درک این مدلهای خوشه ، کلید فهمیدن تفاوت بین الگوریتم‌های مختلف است. مدل‌های خوشه ای معمول عبارتند از:

مدل‌های متصل: به عنوان مثال، خوشه بندی سلسله مراتبی، مدل‌هایی براساس فاصله متصل را ایجاد می‌کند.
مدل‌های مرکزی: به عنوان مثال، الگوریتم k-means ، هر خوشه را با یک بردار متوسط نشان می‌دهد.
مدل‌های توزیع: خوشه‌ها با استفاده از توزیع‌های آماری، مانند توزیع نرمال چند متغیره که در الگوریتم حداکثر انتظار ، استفاده شده‌است.
مدلهای تراکم: به عنوان مثال، DBSCAN و OPTICS خوشه را به عنوان مناطق متراکم متصل در فضای داده تعریف می‌کنند.
مدل‌های زیر فضایی: در biclustering (که به عنوان خوشه مشترک یا خوشه ای دو حالت شناخته می‌شود)، خوشه‌ها با هر دو اعضای خوشه و ویژگی‌های مرتبط مدل سازی می‌شوند.
مدل‌های گروهی: برخی از الگوریتم‌ها یک مدل تصحیح شده برای نتایج خود را ارائه نمی دهند و فقط اطلاعات گروه بندی را ارائه می دهند.
مدل‌های مبتنی بر گراف: یک کلاس، یعنی یک زیر مجموعه از گره‌ها در یک گراف به طوری که هر دو گره در زیر مجموعه با یک لبه متصل می‌شود که می‌تواند به عنوان یک شکل اولیه از خوشه مورد توجه قرار گیرد.
مدل‌های عصبی: شبکه عصبی غیرقابل نظارت ، شناخته شده‌ترین نقشه خود سازمانی است و معمولا این مدل‌ها می توانند به عنوان مشابه با یک یا چند مدل فوق شامل مدل‌های زیر فضایی، زمانی که شبکه‌های عصبی یک فرم تجزیه و تحلیل مؤلفه اصلی یا مستقل تجزیه و تحلیل المان می‌باشد .

“خوشه بندی” اساسا مجموعه ای از خوشه‌ها است که معمولا شامل تمام اشیاء در مجموعه داده‌ها می‌شود. علاوه بر این، می‌توان رابطه خوشه‌ها را به یکدیگر تعریف کند، به عنوان مثال، سلسله مراتب خوشه‌های تعبیه شده در یکدیگر.

خوشه بندی را می‌توان براساس سختی تمایز به صورت زیر مشخص کرد:

خوشه بندی سخت: هر شیء متعلق به خوشه است یا نه.
خوشه بندی نرم (همچنین: خوشه فازی): هر شیء به درجه خاصی از هر خوشه متعلق است (به عنوان مثال، احتمال وابستگی به خوشه)

همچنین امکان تمایز دقیق تر وجود دارد، مثلا:

خوشه بندی جداسازی دقیق ( پارتیشن بندی): هر شیء دقیقا به یک خوشه متعلق است.
خوشه بندی جداسازی دقیق با ناپیوستگی: اشیاء می توانند به هیچ خوشه ای تعلق نداشته باشند.
خوشه بندی همپوشانی (همچنین: خوشه بندی جایگزین، خوشه بندی چندگانه): اشیاء ممکن است متعلق به بیش از یک خوشه باشد؛ معمولا خوشه‌های سخت را شامل می‌شود
خوشه بندی سلسله مراتبی: اشیایی که متعلق به خوشه فرزند هستند، متعلق به خوشه پدر و مادر هم هستند.
خوشه بندی زیر فضا: در حالی که خوشه بندی همپوشانی، که در یک زیر فضای منحصر به فرد تعریف شده ، انتظار نمی رود که خوشه‌ها با همپوشانی داشته باشند.

الگوریتم

همانطور که در بالا ذکر شد، الگوریتم‌های خوشه بندی را می‌توان بر اساس مدل خوشه ای طبقه بندی کرد. در ادامه نمونه‌های برجسته ای از الگوریتم‌های خوشه بندی بیان شده‌است، زیرا احتمالا بیش از 100 الگوریتم خوشه بندی منتشر شده وجود دارد. همه مدلها برای خوشه هایشان بیان نشده اند، بنابراین نمی توان به راحتی دسته بندی کرد.

الگوریتم خوشه بندی عینی “صحیح” وجود ندارد، اما همانطور که اشاره شد، “خوشه بندی در چشم بیننده است.” بهترین الگوریتم خوشه بندی برای یک مسئله خاص، اغلب باید به صورت تجربی انتخاب شود، مگر اینکه یک دلیل ریاضی برای ترجیح دادن یک مدل خوشه بر دیگری وجود داشته باشد. لازم به ذکر است که یک الگوریتم که برای یک نوع مدل طراحی شده‌است و در یک مجموعه داده ای که شامل تفاوت اساسی مدل است، شکست می خورد. به عنوان مثال، k-means نمیتواند خوشه‌های غیرمحدب را پیدا کند.

خوشه بندی براساس اتصال (خوشه بندی سلسله مراتبی)

خوشه بندی براساس اتصال، که همچنین به عنوان خوشه بندی سلسله مراتبی شناخته می‌شود، بر مبنای ایده اصلی اشیائی است که بیشتر مربوط به اشیای نزدیک، نسبت به اشیاء دورتر است. این الگوریتم‌ها “اشیا” را برای ایجاد “خوشه ها” بر اساس فاصله آن‌ها متصل می‌کنند. خوشه را می‌توان به طورکلی با حداکثر فاصله مورد نیاز برای اتصال قطعات خوشه توصیف کرد. در فاصله‌های مختلف، خوشه‌های متفاوتی شکل می‌گیرند که می‌تواند با استفاده از یک دندروگرام نشان داده شود، که توضیح می‌دهد که نام معمول “خوشه بندی سلسله مراتبی” از آن می آید: این الگوریتم‌ها یک پارتیشن بندی مچموعه داده را ارائه نمی دهند، بلکه یک سلسله مراتب گسترده ای از خوشه‌هایی که در فاصله‌های معینی با یکدیگر ادغام می‌شوند، ارائه میدهد. در یک دندروگرام، محور y نشان دهنده فاصله ای است که خوشه‌ها ادغام می‌کنند، در حالی که اشیا در امتداد محور x قرار می‌گیرند به طوری که خوشه‌ها با هم مخلوط نمی‌شوند.

خوشه بندی سلسله مراتبی شامل دو نوع خوشه بندی می‌باشد:

single linkage -1 این روش که به روش Bottom-Up و Agglomerative نیز معروف است روشی است که در آن ابتدا هر داده به عنوان یک خوشه در نظر گرفته می‌شود. در ادامه با به کارگیری یک الگوریتم هر بار خوشه‌های دارای ویژگی‌های نزدیک به هم با یکدیگر ادغام شده و این کار ادامه می‌یابد تا به چند خوشهٔ مجزا برسیم. مشکل این روش حساس بودن به نویز و مصرف زیاد حافظه می‌باشد.

complete linkage -2 در این روش که به روش Top-Down و Divisive نیز معروف است ابتدا تمام داده‌ها به عنوان یک خوشه در نظر گرفته شده و با به کارگیری یک الگوریتم تکرار شونده هربار داده‌ای که کمترین شباهت را با داده‌های دیگر دارد به خوشه‌های مجزا تقسیم می‌شود. این کار ادامه می‌یابد تا یک یا چند خوشه یک عضوی ایجاد شود. مشکل نویز در این روش برطرف شده‌است.

مثال هایی از خوشه linkage

خوشه بندی براساس centroid

در خوشه بندی براساس centroid، خوشه‌ها با یک بردار مرکزی نشان داده می‌شوند، که ممکن است لزوما جزء مجموعه داده نباشد. هنگامی که تعدادی از خوشه‌ها به k متصل می‌شوند، خوشه بندی k-means یک تعریف رسمی را به عنوان یک مسئله بهینه سازی ارائه می‌دهد.

روش میانگین k در عین سادگی یک روش بسیار کاربردی و پایه چند روش دیگر مثل خوشه بندی فازی و Segment-wise distributional clustering Algorithm می‌باشد.روش کار به این صورت است که ابتدا به تعداد دلخواه نقاطی به عنوان مرکز خوشه در نظر گرفته می‌شود. سپس با بررسی هر داده، آن را به نزدیک‌ترین مرکز خوشه نسبت می‌دهیم. پس از اتمام این کار با گرفتن میانگین در هر خوشه می‌توانیم مراکز خوشه و به دنبال آن خوشه‌های جدید ایجاد کنیم. (با تکرار مراحل قبل)از جمله مشکلات این روش این است که بهینگی آن وابسته به انتخاب اولیه مراکز بوده و بنابراین بهینه نیست. مشکلات دیگر آن تعیین تعداد خوشه‌ها و صفر شدن خوشه‌ها می‌باشد.

K-means دارای تعدادی خواص نظری است. اول، فضای داده را به یک ساختار معروف به یک نمودار Voronoi تقسیم می‌کند. دوم، به لحاظ مفهومی نزدیک به طبقه بندی نزدیکترین همسایه است و به همین علت در یادگیری ماشین محبوب است. سوم، می‌توان آن را به عنوان تنوع خوشه بندی براساس مدل مشاهده کرد.

مثال هایی از خوشه بندی k-means

خوشه بندی براساس توزیع

این مدل خوشه بندی که دقیقا مربوط به آمار می‌باشد، بر اساس مدل‌های توزیع است.خوشه‌ها به راحتی می توانند به عنوان اشیایی تعریف می‌شوند که به احتمال زیاد ب توزیع یکسانی دارند. یک ویژگی خوب این رویکرد این است که با نمونه برداری از اشیاء تصادفی از یک توزیع، دقیقا شبیه نحوه تولید مجموعه داده‌های مصنوعی است. مبنای نظری این روش‌ها عالی است، ولی مشکل اصلی overfitting دارند، مگر اینکه محدودیت‌ها بر پیچیدگی مدل قرار بگیرد.

یک روش شناخته شده ،مدل مخلوط گاوس (با استفاده از الگوریتم حداکثر سازی انتظار) است. مجموعه داده‌ها معمولا با یک ثابت (برای جلوگیری از overfitting) تعداد توزیع‌های گاوسی که به صورت تصادفی استفاده شده و به منظور مناسب تر کردن مجموعه داده مدل ، پارامترهای آن به‌طور تکراری بهینه شده‌است که به یک بهینه محلی همگرا می‌شود، بنابراین در طول چند اجرا ممکن است نتایج متفاوتی تولید کند. به منظور به دست آوردن خوشه بندی سخت، اشیاء اغلب به توزیع گاوسی که به احتمال زیاد متعلق به آنهاست، اختصاص داده است که برای خوشه بندی نرم، اینکار لازم نیست.خوشه بندی مبتنی بر توزیع، مدل‌های پیچیده ای را برای خوشه‌ها ایجاد می‌کند که می‌تواند همبستگی و وابستگی ویژگی را نشان دهد.

مثال های Expectation-maximization (EM)

خوشه بندی براساس Density

در این تکنیک این اصل مطرح می‌شود که خوشه‌ها مناطقی با چگالی بیشتر هستند که توسط مناطق با چگالی کمتر از هم جدا شده‌اند. یکی از مهم‌ترین الگوریتم‌ها در این زمینه الگوریتم DBSCAN است.

روش این الگوریتم به این صورت است که هر داده متعلق به یک خوشه در دسترس چگالی سایر داده‌های همان خوشه است، ولی در دسترسی چگالی سایر داده‌های خوشه‌های دیگر نیست.(چگالی داده همسایگی به مرکز داده و شعاع همسایگی دلخواه ε است)مزیت این روش این است که تعداد خوشه‌ها به صورت خودکار مشخص می‌شود. در تشخیص نویز نیز بسیار کاراست.

مثال هایی برای خوشه بندی براساس Density

پیشرفت های اخیر

در سال‌های اخیر تلاش‌های قابل توجهی در بهبود عملکرد الگوریتم‌های موجود انجام شده‌است.با توجه به نیازهای جدید به پردازش داده‌های خیلی بزرگ، تمایل به کاربرد خوشه‌های تولید شده برای عملکرد تجاری افزایش یافته‌است. این امر منجر به توسعه روش‌های پیش خوشه سازی مانند خوشه بندیcanopy می‌شود که می‌تواند داده‌های حجیم را به‌طور مؤثر پردازش کند.

برای داده‌های با ابعاد بزرگ، بسیاری از روش‌های موجود به علت ابعاد شکست خورده است، که باعث می‌شود که توابع خاص فاصله در فضاهای بزرگ بعدی مشکل ساز باشند. این باعث شد که الگوریتم‌های خوشه بندی جدید برای داده‌های با ابعاد بزرگ ، بر خوشه بندی زیر فضایی تمرکز کنند و استفاده شود.

چندین سیستم خوشه بندی مختلف مبتنی بر اطلاعات متقابل پیشنهاد شده‌است. یکی از آن ها، تغییرات اطلاعات مارینا مالگا است که یکی دیگر از خوشه بندی سلسله مراتبی را فراهم می‌کند. با استفاده از الگوریتم‌های ژنتیکی، طیف گسترده ای از تناسب توابع مختلف، از جمله اطلاعات متقابل، می‌تواند بهینه سازی شود،پیشرفت اخیر در علوم کامپیوتری و فیزیک آماری، منجر به ایجاد انواع جدیدی از الگوریتم‌های خوشه بندی شده‌است.

خوشه بندی (Clustering) قسمت 1
خوشه بندی (Clustering) قسمت 2
خوشه بندی (Clustering) قسمت 3

دسامبر 7, 2019/0 دیدگاه /توسط daliri