بایگانی‌های lng lotd

بایگانی برچسب برای: lng lotd

مدل مخفی مارکوف (Hidden Markov Model) قسمت 3

انواع مدل‌های مخفی مارکوف و HMM پیوسته

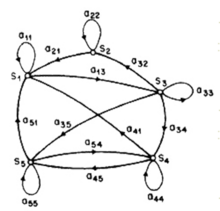
همان‌طور که گفته شد نوع خاصی از HMM وجود دارد که در آن تمام حالات موجود با یکدیگر متصل هستند. لیکن مدل مخفی مارکوف از لحاظ ساختار و اصطلاحاً توپولوژی انواع مختلف دارد. همان‌طور که گفته شد برای مدل ارگودیک برای تمام i و jها $\ a_{ij}>0$ است و ساختار مدل مثل یک گفتار کامل است که راسها در آن دارای اتصالات بازگشتی نیز می‌باشند. لیکن برای کاربردهای متفاوت و با توجه به پیچیدگی فرایند نیاز به ساختار متفاوتی وجود دارد. از جمله این ساختارها که به شکل گسترده‌ای در کاربردهای شناسایی گفتار مبتنی بر واج و شناسایی گوینده مورد استفاده قرار می‌گیرد، مدل چپ به راست یا مدل بکیس است. این مدل که ساختار آن را در شکل ۲ نیز می‌بینید، دارای اتصالات چپ به راست است و برای مدل کردن سیگنالهایی که خواص آن‌ها با زمان تغییر می‌کند مورد استفاده قرار می‌گیرد. در مدل چپ به راست تنها یک حالت ورودی وجود دارد که همان حالت اول است و به این ترتیب:

$\pi _{t}={\begin{cases}0,&\,i\neq 1\\1,&\,i\neq 1\end{cases}}$ مدلهای ارگودیک و چپ به راست مدل‌های HMM پایه هستند و در پردازش گفتار نیز بیشترین کاربرد را دارا می‌باشند. هرچند می‌توان با اتصال چندین مدل یا تغییر در ساختار اتصالات آن مدلهایی با انعطاف‌پذیری بیشتری ایجاد نمود. شکل ۲-ج یک نمونه از مدل موازی چپ به راست، که شامل دو مدل چپ به راست است، را نشان می‌دهد.

در قسمت‌های قبل مدل‌های HMM برای مجموعه مشاهدات گسسته را مورد بررسی قرار دادیم. اگر چه می‌توان با چندی‌سازی تمام فرایندهای پیوسته را به فرایندهای با دنباله مشاهدات گسسته تبدیل نمود، اما این کار ممکن است باعث افت مدل شود. در مدل HMM پیوسته احتمال قرار گرفتن مشاهدات در یک حالت را با توابع چگالی احتمال نشان می‌دهند. در این شرایط برای هر حالت i و ورودی O، احتمال مشاهده $\ b_{t}(O)$ به صورت یک توزیع شامل M مخلوط نشان داده می‌شود:

$\ b_{t}(O)=\sum _{m=1}^{M}c_{im}R(O,\mu _{im},U_{im})$

$\ c_{im}\geq 0,1\leq i\leq N,1\leq m\leq M$

مدل مخلوط گاوسی

مدل مخلوط گوسی یکی از مهمترین روش‌های مدل کردن سیگنال است که در واقع شبیه یک HMM یک حالته است که تابع چگالی احتمال آن حالت دارای چندین مخلوط نرمال می‌باشد. احتمال تعلق بردار آزمایشیd به یک مدل مخلوط گاوسی دارای M مخلوط به شکل زیر بیان می‌شود:

$P(x|GMM)=\sum _{t=1}^{M}c_{t}.N(\mu _{t},\Sigma _{t}),$

که در آن $\ c_{t}$ وزن مخلوط $\mu _{t}$ و $\Sigma _{t}$ به ترتیب بردار میانگین و ماتریس کوواریانس توزیع نرمال هستند. ماتریس کوواریانس مدل GMM معمولاً به صورت قطری در نظر گرفته می‌شود، گرچه امکان استفاده از ماتریس کامل نیز وجود دارد.

برای به‌دست آوردن پارامترهای مدل GMM، شامل وزن مخلوط‌های گاوسی و میانگین و کواریانس توزیع‌ها، از الگوریتم ماکزیمم نمودن امید ریاضی(EM)استفاده می‌شود. باید توجه داشت که تعداد مخلوطهای گاوسی با تعداد نمونه‌های موجود آموزشی رابطه مستقیم دارند و نمی‌توان با مجموعه داده‌ای ناچیز یک مدل GMM دارای تعداد بیش از حد از مخلوطها را آموزش داد. در تشکیل و آموزش مدل GMM مانند تمام روش‌های تشکیل مدل رعایت نسبت میزان پیچیدگی مدل و نمونه‌های آموزشی الزامی می‌باشد.

فرضیات تئوری مدل مخفی مارکوف

برای اینکه مدل مخفی مارکوف از لحاظ ریاضی و محاسباتی قابل بیان باشد فرضهای زیر در مورد آن در نظر گرفته می‌شود.

۱- فرض مارکوف

با داشتن یک مدل مخفی مارکوف، احتمال انتقال از حالت i به حالت j به صورت زیر تعریف می‌شود:

$\ a_{ij}=p(q_{t+1}|q_{t}=i)$

به بیان دیگر فرض می‌شود که حالت بعدی تنها به حالت فعلی بستگی دارد. مدل حاصل از فرض مارکوف یک مدل HMM مرتبه صفر می‌باشد. در حالت کلی، حالت بعدی می‌تواند با k حالت قبلی وابسته باشد. این مدل که مدل HMM مرتبه k ام گفته می‌شود، با استفاده از احتمالات انتقال به صورت زیر تعریف می‌گردد.

$\ a_{i1}a_{i2}a_{i3}a{i4}...=p(q_{t+1}=j|q_{t}=i_{1},q_{t-1}=i_{2}....,q_{t-k+1}=i_{k},1\leq i_{1},i_{2},...i_{k},j\leq N))$

به نظر می‌رسد که یک مدل HMM از مرتبه بالاتر باعث افزایش پیچیدگی مدل می‌شود. علی‌رغم اینکه مدل HMM مرتبه اول متداول‌ترین مدل است، برخی تلاشها برای استفاده از مدل‌های دارای مرتبه بالاتر نیز در حال انجام می‌باشد.

۲- فرض ایستایی (stationarity)

در اینجا فرض می‌شود که احتمال انتقال در بین حالات از زمان واقعی رخداد انتقال مستقل است. در این صورت می‌توان برا ی هر $\ t_{1},t_{2}$ نوشت

$\ p(q_{t_{1}+1}=j|q_{t_{1}}=i)=p(q_{t_{2}+1}=j|q_{t_{2}}=i$

۳- فرض استقلال خروجی

در این حالت فرض می‌شود که خروجی (مشاهدات) فعلی به صورت آماری از خروجی قبلی مستقل است. می‌توان این فرض را با داشتن دنباله‌ای از خروجی‌ها مانند بیان نمود:

$\ O=o_{1},o_{2},....o_{T}$

آنگاه مطابق با این فرض برای مدل HMM با نام $\ \lambda$ خواهیم داشت:

$\ p(O|q_{1},q_{2},..q_{T},\lambda )={\begin{matrix}\prod _{t=1}^{T}p(O_{t}|q_{t},\lambda )\end{matrix}}$

اگر چه بر خلاف دو فرض دیگر این فرض اعتبار کمتری دارد. در برخی حالات این فرضیه چندان معتبر نیست و موجب می‌شود که مدل HMM با ضعفهای عمده‌ای مواجه گردد.

مسئله ارزیابی و الگوریتم پیشرو (forward)

در این حالت مسئله این است که با داشتن مدل $\lambda =(A,B,\pi )$ و دنباله مشاهدات $O=\{O_{1},O_{2},...,O_{T}\}$ باید مقدار $\ P(O|\lambda )$ را پیدا نماییم. می‌توانیم این مقدار را با روش‌های آماری مبتنی بر پارامترها محاسبه نماییم. البته این کار به محاسباتی با پیچیدگی $\ O(N^{T})$ احتیاج دارد. این تعداد محاسبات حتی برای مقادیر متوسط t نیز بسیار بزرگ است. به همین دلیل لازم است که راه دیگری برای این محاسبات پیدا نماییم. خوشبختانه روشی ارائه شده‌است که پیچیدگی محاسباتی کمی دارد و از متغیر کمکی $\ a_{t}(i)$ با نام متغیر پیشرو استفاده می‌کند.

متغیر پیشرو به صورت یک احتمال از دنباله مشاهدات $O=\{O_{1},O_{2},...,O_{t}\}$ تعریف می‌شود که در حالت i خاتمه می‌یابد. به بیان ریاضی:

$\alpha _{t}(i)=p\{O_{1},O_{2},...,O_{t},q_{t}=i|\lambda \}$ آنگاه به سادگی مشاهده می‌شود که رابطه بازگشتی زیر برقرار است.

$\ a_{t+1}(j)=b_{j}(O_{t+1}\sum _{i=1}^{N})a_{t}(i)a_{ij},1\leq j\leq N,1\leq t\leq T-1$

که در آن

$\ a_{1}(j)=\pi _{j}b_{j}(O_{1}),1\leq j\leq N$

با داشتن این رابطه بازگشتی می‌توانیم مقدار زیر را محاسبه نماییم.

$\ a_{T}(i),1\leq i\leq N$

و آنگاه احتمال $\ P(O|\lambda )$ به صورت زیر محاسبه خواهد شد:

$p\{O|\lambda \}=\sum _{i=1}^{N}a_{T}(i)$

پیچیدگی محاسباتی روش فوق که به الگوریتم پیشرو معروف است برابر با $\ O(N^{2}T)$ است، که در مقایسه با حالت محاسبه مستقیم که قبلاً گفته شد، و دارای پیچیدگی نمایی بود، بسیار سریعتر است.

روشی مشابه روش فوق را می‌توان با تعیین متغیر پسرو، $\beta _{t}(i)$ ، به عنوان احتمال جزئی دنباله مشاهدات $O=\{O_{t+1},O_{t+2},...,O_{T}\}$ در حالت i تعریف نمود. متغیر پیشرو را می‌توان به شکل زیر نمایش داد.

$\beta _{t}(i)=p\{O_{t+1},O_{t+2},...,O_{T}|q_{t}=i,\lambda \}$

مانند روش پیشرو یک رابطه بازگشتی به شکل زیر برای محاسبه $\beta _{t}(i)$ وجود دارد.

$\beta _{t}(i)=\sum _{i=1}^{N}\beta _{t+1}(j)a_{ij}b_{j}(O_{t+1}),1\leq i\leq N,1\leq t\leq T-1$

که در آن

$\beta _{t}(i)=1,1\leq i\leq N$

می‌توان ثابت کرد که

$\ a_{t}(i)\beta _{t}(i)=p\{O,q_{t}=i|\lambda \},1\leq i\leq N,1\leq t\leq T$

آنگاه می‌توان با کمک هر دو روش پیشرو و پسرو مقدار احتمال $\ P(O|\lambda )$ را محاسبه نمود.

$p\{O|\lambda \}=\sum _{i=1}^{N}p\{O,q_{t}=i|\lambda \}=\sum _{i=1}^{N}a_{t}(i)\beta _{t}(i)$ رابطه فوق بسیار مهم و مفید است و بخصوص برای استخراج روابط آموزش مبتنی بر گرادیان لازم می‌باشد.

مدل مخفی مارکوف (Hidden Markov Model) قسمت 1
مدل مخفی مارکوف (Hidden Markov Model) قسمت 2
مدل مخفی مارکوف (Hidden Markov Model) قسمت 3
مدل مخفی مارکوف (Hidden Markov Model) قسمت 4

نوامبر 3, 2019/0 دیدگاه /توسط hgadmin

مدل مخفی مارکوف (Hidden Markov Model) قسمت 2

دسته‌بندی نشده

کاربردهای مدل مخفی مارکوف

بازشناسی گفتار
ترجمه ماشینی
پیش‌بینی ژن
هم‌ترازسازی توالی
تشخیص فعالیت
تاشدگی پروتئین
تشخیص چهره

تاریخچه

مدل مخفی مارکوف برای اولین بار در مجموعه‌مقالات آماری leonard E.Baum و سایر نویسندگان در نیمه دوم دهه ۱۹۶۰ توضیح داده شد. یکی از اولین کاربردهای HMM تشخیص گفتار بوده که در اواسط دههٔ ۱۹۷۰ شروع شد. HMM در نیمهٔ دوم ۱۹۸۰ وارد حوزهٔ آنالیز دنباله‌های بیولوژیکی، به‌طور خاص DNA شد. از آن پس، کاربرد آن در بیوانفورماتیک گسترش یافت.

انواع مدل مخفی مارکوف

مدل پنهان مارکوف می‌تواند فرایندهای پیچیده مارکوف را که حالتها بر اساس توزیع احتمالی مشاهدات را نتیجه می‌دهند، مدل کند. به‌طور مثال اگر توزیع احتمال گوسین باشد در چنین مدل مارکوف پنهان خروجی حالتها نیز از توزیع گوسین تبعیت می‌کنند. علاوه بر این مدل مخفی مارکوف می‌تواند رفتارهای پیچیده‌تر را نیز مدل کند. جایی که خروجی حالت‌ها از ترکیب دو یا چند توزیع گوسین پیروی کند که در این حالت احتمال تولید یک مشاهده از حاصلضرب گوسین انتخاب شدهٔ اولی در احتمال تولید مشاهده از گوسین دیگر به دست می‌آید.

فرایند مارکوف گسسته

یک سیستم مانند شکل زیر را که در هر لحظه در یکی از حالت متمایز S1,… ,SN است در نظر بگیرید. در زمان‌های گسسته و با فواصل منظم، حالت سیستم با توجه به مجموعه‌ای از احتمالات تغییر می‌کند. برای زمان‌های… ,t=۱٬۲ حالت در لحظه t را با qt نشان می‌دهیم. برای یک توصیف مناسب از سیستم فعلی نیاز به دانستن حالت فعلی در کنار تمام حالات قبلی می‌باشد. برای یک حالت خاص از زنجیره مارکوف مرتبه اول، توصیف احتمالاتی تنها با حالت فعلی و حالت قبلی مشخص می‌شود.

\ P(q_{t}=S_{j}|q_{t-1}=S_{i},q_{t-2}=S_{k},...)=

\ P(q_{t}=S_{j}|q_{t-1}=S_{i})

حال تنها فرایندهایی را در نظر می‌گیریم که در آن‌ها سمت راست رابطه فوق مستقل از زمان است و به همین دلیل ما مجموعه‌ای از احتمالات انتقال بین حالت‌ها را خواهیم داشت.

$\ a_{ij}=P(q_{t}=S_{j}|q_{t-1}=S_{i})\qquad i\geq 1,N\geq j$

که در آن احتمال انتقال بین حالات دارای خواص زیر است.

$a_{ij}\geq 0$

$\sum _{j=1}^{N}a_{ij}=1$

فرایند تصادفی فوق را مدل مارکوف قابل مشاهده می‌گویند زیرا خروجی مدل مجموعه‌ای از حالات است که قرار گرفتن در آن‌ها متناظر با یک مشاهده می‌باشد. ما می‌توانیم دنباله مشاهدات مورد انتظار خود را تولید کنیم و احتمال وقوع آن در زنجیره مارکوف را محاسبه نماییم. برای مثال با داشتن دنباله مشاهدات $\ O={q_{1},...,q_{t}}$ احتمال وقوع آن به صورت زیر بیان می‌شود.

$\ P(O|Model)=P({q_{1},q_{2},...,q_{2}}|Model)$

$\ P(q_{1}).P(q_{2}|q_{1}).P(q_{3}|q_{2})...P(q_{t}|q_{t-1})$

یکی دیگر از مواردی که مطرح می‌شود این است که اگر سیستم در حالت $\ q_{i}$ باشد با چه احتمالی به حالت $\ q_{j}$ می‌رود و با چه احتمالی در همان حالت $\ q_{i}$ باقی می‌ماند.

مرتبه مدل مارکوف

۱- مدل مارکوف مرتبه صفر

یک مدل مارکوف از مرتبه صفر هیچ حافظه‌ای ندارد و برای هر t و t’ در دنباله سمبل‌ها، $\ pr(X_{t}=S_{i})=pr(X_{t'}=S_{i})$ خواهد بود. مدل مارکوف از مرتبه صفر مانند یک توزیع احتمال چند جمله‌ای می‌باشد.

۲- مدل مارکوف مرتبه اول

یک مدل مارکوف مرتبه اول دارای حافظه‌ای با طول ۱ می‌باشد. توزیع احتمال در این مدل به صورت زیر مشخص می‌شود.

$\ pr(X_{t}=S_{i}|X_{t-1}=S_{j}),fori=1..k,j=1..k$

تعریف فوق مانند این است که k مدل مارکوف در مرتبه صفر برای هر $\ S_{j}$ داشته باشیم.

۳- مدل مارکوف مرتبه m ام

مرتبه یک مدل مارکوف برابر است با طول حافظه‌ای که مقادیر احتمال ممکن برای حالت بعدی به کمک آن محاسبه می‌شود. برای مثال، حالت بعدی در یک مدل مارکوف از درجه ۲ (مدل مارکوف مرتبه دوم) به دو حالت قبلی آن بستگی دارد.

مثال ۱: برای مثال اگر یک سکه معیوب A داشته باشیم که احتمالات شیر یا خط آمدن برای آن یکسان نباشد، می‌توان آن را با یک مدل مارکوف درجه صفر با استفاده از احتمالات (pr(H و (pr(H توصیف نمود.

pr(H)=0.6, pr(T)=۰٫۴

مثال ۲: حال فرض کنید که سه سکه با شرایط فوق در اختیار داریم. سکه‌ها را با اسامی B, A و C نام‌گذاری می‌نماییم. آنگاه برای توصیف روال زیر به یک مدل مارکوف مرتبه اول نیاز داریم:

فرض کنید سکه X یکی از سکه‌های A یا B باشد.
مراحل زیر را تکرار می‌کنیم.

a) سکه X را پرتاب می‌کنیم و نتیجه را می‌نویسیم.

b) سکه C را نیز پرتاب می‌کنیم.

c) اگر سکه C خط آمد، آنگاه سکه X را تغییر می‌دهیم (A را با B یا B را با A جایگزین می‌کنیم) و در غیر این صورت تغییری در سکه‌ها نمی‌دهیم.

انجام روال فوق مدل مارکوف مرتبه اول زیر را نتیجه خواهد داد.

یک پردازش مارکوفی مانند نمونه فوق در طول پیمایش احتمالات، یک خروجی نیز خواهد داشت. یک خروجی نمونه برای پردازش فوق می‌تواند به شکل HTHHTHHttthtttHHTHHHHtthtthttht باشد.

مدل مارکوف فوق را می‌توان به صورت نموداری از حالات و انتقال‌ها نیز نشان داد. کاملاً مشخص است که این‌گونه بازنمایی از مدل مارکوف مانند بازنمایی یک ماشین انتقال حالت محدود است که هر انتقال با یک احتمال همراه می‌باشد

مدل مخفی مارکوف (HMM)

تا اینجا ما مدل مارکوف، که در آن هر حالت متناظر با یک رویداد قابل مشاهده بود را معرفی نمودیم. در این بخش تعریف فوق را گسترش می‌دهیم، به این صورت که در آن، مشاهدات توابع احتمالاتی از حالتها هستند. در این صورت مدل حاصل یک مدل تصادفی با یک فرایند تصادفی زیرین است که پنهان است و تنها توسط مجموعه‌ای از فرایندهای تصادفی که دنباله مشاهدات را تولید می‌کنند قابل مشاهده است.

برای مثال فرض کنید که شما در یک اتاق هستید و در اتاق مجاور آن فرد دیگری سکه‌هایی را به هوا پرتاب می‌کند و بدون اینکه به شما بگوید این کار را چگونه انجام می‌دهد و تنها نتایج را به اطلاع شما می‌رساند. در این حالت شما با فرایند پنهان انداختن سکه‌ها و با دنباله‌ای از مشاهدات شیر یا خط مواجه هستید. مسئله‌ای که اینجا مطرح می‌شود چگونگی ساختن مدل مارکوف به منظور بیان این فرایند تصادفی است. برای مثال اگر تنها مشاهدات حاصل از انداختن یک سکه باشد، می‌توان با یک مدل دو حالته مسئله را بررسی نمود. یک مدل مخفی مارکوف را می‌توان با تعیین پارامترهای زیر ایجاد نمود:

تعداد حالات ممکن: تعداد حالتها در موفقیت مدل نقش به سزایی دارد و در یک مدل مخفی مارکوف هر حالت با یک رویداد متناظر است. برای اتصال حالتها روش‌های متفاوتی وجود دارد که در عمومی‌ترین شکل تمام حالتها به یکدیگر متصل می‌شوند و از یکدیگر قابل دسترسی می‌باشند. تعداد مشاهدات در هر حالت: تعداد مشاهدات برابر است با تعداد خروجیهایی که سیستم مدل شده خواهد داشت.

N تعداد حالتهای مدل M تعداد سمبلهای مشاهده در الفبا، اگر مشاهدات گسسته باشند آنگاه M یک مقدار نا محدود خواهد داشت.

$\ A={a_{ij}}$

$\ A=[a_{ij}]$ ماتریس انتقال حالت:یک مجموعه از احتمالات در بین حالت‌ها

$\ a_{ij}=p(q_{t+1}=j|q_{t}=i),\qquad i\geq 1,N\geq j$

که در آن $\ q_{t}$ بیانگر حالت فعلی می‌باشد. احتمالات انتقال باید محدودیتها طبیعی یک توزیع احتمال تصادفی را برآورده نمایند. این محدودیتها شامل موارد زیر می‌گردند

$\ a_{ij}\geq 0,\qquad i\geq 1,N\geq j$

$\sum _{j=1}^{N}a_{ij}=1,\qquad 1\leq i\leq N$

برای حالات مدل ارگودیک برای تمامi وjها مقدار $\ a_{ij}$ بزرگتر از صفر است و در موردی که اتصالی بین حالات وجود ندارد $\ a_{ij}=0$ است.

توزیع احتمال مشاهدات: یک توزیع احتمال برای هر یک از حالتها

$\ B={b_{j}(k)}$

$\ b_{j}(k)=p{o_{t}=v_{k}|q_{t}=j},\qquad 1\leq j\leq N,\qquad 1\leq k\leq M$

که در آن $\ v_{k}$ بیانگرkامین سمبل مشاهده شده در الفبا است و $\ o_{t}$ بیانگر بردار پارامترهای ورودی فعلی می‌باشد. در مورد مقادیر احتمال حالتها نیز شرایط موجود در نظریه احتمال باید رعایت گردند.

$\ b_{j}(k)\qquad 1\leq j\leq N,\qquad 1\leq K\leq M$

$\sum _{K=1}^{M}b_{j}(k)=1,\qquad 1\leq j\leq N$

اگر مشاهدات به صورت پیوسته باشند، باید به جای احتمالهای گسسته از یک تابع چگالی احتمال پیوسته استفاده شود. معمولاً چگالی احتمال به کمک یک مجموع وزندار از M توزیع نرمال μ تخمین زده می‌شود.

$\ b_{j}(o_{t})=\Sigma _{m=1}^{M}c_{jm}\mu (\mu _{jm},\Sigma _{jm},o_{t})$

که در آن $\ \mu _{jm}$ ، $\ C_{jm}$ , $\ \Sigma _{jm}$ , به ترتیب ضریب بردار میانگین، ضریب وزندهی و ماتریس کواریانس می‌باشند. در رابطه فوق مقادیر $\ c_{jm}$ باید شرایط زیر را ارضا نماید: