بایگانی برچسب برای: hk

این الگوریتم (تشخیص پلاک خودرو) با نرم افزار MATLAB 2011 نوشته شده است برای خواندن پلاک که بدون نویز و خرابی هستند خوب جواب میدهد…البته دیتا بیس کاراکترها رو خودتون به راحتی میتوانید بیشتر کنید تا پاسخ دهی قویتر شود …فعلا فقط یک تصویر به عنوان آزمایش جهت تست برنامه قرار داده شده .

همچنین به علت ضیق وقت قسمت شناسای کاراکترها و تبدیل آنها به عدد و حروف فارسی رو قوی نکردم…شما میتونید این قسمت را برای جوابدهی بهتر دستکاری کنید… در ضمن اگر خواستین از نحوه فرمولبندی و کارکرد برنامه سر دربیارید حدود 20 صفحه هم گزارش تهیه شده ، فایل پاور پوینتی که برای ارائه پروژه تشخیص پلاک خودرو آماده شده نیز آپلود گردیده است.

فقط قبل از اجرای برنامه این مراحل رو طی کنید:
1- مسیر عکس خودرو(glx.jpg) رو وارد کنید
2-دیتا بیس (فایل زیپ) رو دانلود کنید
3-مسیر دیتا-بیس کاراکترها رو درست وارد کنید.
4-برنامه رو اجرا کنید-نتایج رو صفحه کامند matlab نمایش داده میشود.
5-هر جا خواستید از پشت دستور imshow و figure علامت % رو حذف کنید تا کارهای که روی تصویر انجام میشود رو مرحله به مرحله ببینید.
6-برنامه را اجرا کنید و نتایج را در صفحه متلب ببیند.

موضوع: آموزش تشخیص پلاک خودرو های ایرانی توسط نرم افزار متلب

تعداد صفحات پی دی اف : 18

تعداد صفحات پاور پوینت : 18

سورس کد : نرم افزار متلب Matlab

قیمت : رایگان

کلمه عبور فایل : behsanandish.com

دانلود

نکته : شرکت بهسان اندیش تولید کننده سامانه های هوشمند مفتخر به تولید یکی از دقیقترین و سریعترین سامانه های جامع کنترل تردد خودرو می باشد که می توانید جهت آشنایی با این محصول به لینک :سامانه جامع کنترل تردد خودرو بهسان(پلاک خوان) مراجعه فرمایید.

سورس برنامه در نرم افزار متلب:


clear all
close all
clc

p0=imread('E:\NIT\DIP\dip data proj\car\glx.jpg');
p=rgb2gray(p0);
p=im2double(p);

f=fspecial('gaussian');
pf=imfilter(p,f,'replicate');
%imshow(pf)
%figure
Pm=mean2(pf); %Average or mean of matrix elements
Pv=((std2(pf))^2); %the variance of an M-by-N matrix is the square of the standard deviation
T=Pm+Pv;

% taerife astane............................................
[m n]=size(pf);
for j=1:n
 for i=1:m
 if pf(i,j)&amp;amp;gt;T;
 pf(i,j)=1;
 else
 pf(i,j)=0;
 end
 end
end

ps=edge(pf,'sobel');
%imshow(ps)
%figure
pd=imdilate(ps,strel('diamond',1));
pe=imerode(pd,strel('diamond',1));
pl=imfill(pe,'holes');
[m n]=size(pl);

%barchasb gozary..............................................
pll=bwlabel(pl);
stat =regionprops(pll,'Area','Extent','BoundingBox','Image','Orientation','Centroid');
index = (find([stat.Area] == max([stat.Area]))); %meghdare barchasb dakhele bozorgtarin masahat ra mikhanad
ppout=stat(index).Image;
%imshow(ppout);
%figure

% biron keshidane mokhtasate pelak.............................
x1 = floor(stat(index).BoundingBox(1)); %shomare stone awalin pixel (B = floor(A) rounds the elements of A to the nearest integers less than or equal to A)
x2 = ceil(stat(index).BoundingBox(3)); %pahnaye abject dar sathe ofoghi(B = ceil(A) rounds the elements of A to the nearest integers greater than or equal to A)
y1 = ceil(stat(index).BoundingBox(2)); %shomare satre avalin pixel(B = ceil(A) rounds the elements of A to the nearest integers greater than or equal to A)
y2 = ceil(stat(index).BoundingBox(4)); %pahnaye abject dar sathe amodi(B = ceil(A) rounds the elements of A to the nearest integers greater than or equal to A)
bx=[y1 x1 y2 x2];
ppc=imcrop(p0(:,:,:),[x1,y1,x2,y2]);
%imshow(ppc)
%figure
ppg=imcrop(p(:,:),[x1,y1,x2,y2]);
%imshow(ppg)
%figure

%plate enhancment..............................................
ppcg=rgb2gray(ppc);
ppcg=imadjust(ppcg, stretchlim(ppcg), [0 1]); % specify lower and upper limits that can be used for contrast stretching image(J = imadjust(I,[low_in; high_in],[low_out; high_out]))
ppg=im2double(ppcg);
pb=im2bw(ppg);%im2bw(I, level) converts the grayscale image I to a binary image
%imshow(pb)
%figure

%rotate correction..............................................
if abs(stat(index).Orientation) &amp;amp;gt;=1; %The orientation is the angle between the horizontal line and the major axis of ellipse=angle
 ppouto=imrotate(ppout,-stat(index).Orientation); %B = imrotate(A,angle) rotates image A by angle degrees in a counterclockwise direction around its center point. To rotate the image clockwise, specify a negative value for angle.
 pbo=imrotate(pb,-stat(index).Orientation);
 angle = stat(index).Orientation;
else
 pbo=pb;
end;
%imshow(pbo)

pbod=imdilate(pbo,strel('line',1,0));
pbodl=imfill(pbod,'holes');
px = xor(pbodl , pbod);

pz= imresize(px, [44 250]); % 4*(57*11)=(chahar barabar size plake khodroye irani)

%barchasb zanye plak..........................................
stat1 = regionprops(bwlabel(pz,4),'Area','Image');
index1 = (find([stat1.Area] == max([stat1.Area])));
maxarea =[stat1(index1).Area];%braye hazfe neweshteye iran va khatahaye ehtemali
pzc=bwareaopen(pz,maxarea-200); %maxarea(1,1) meghdare structur ra adres dehi mikonad,va migoyad object haye ka mte z an ra hazf konad
%histogram plak......
%v=sum(pzc);
%plot(v);

%biron keshidan karakterha......................................
stat2=regionprops(pzc,'Area','BoundingBox','Image','Orientation','Centroid');
cx=cell(1,8);
for i=1:8
 x=stat2(i).Image;
 rx=imresize(x, [60 30]);
 %imshow(rx)
 %figure
 cx{1,i}=rx;
 %fx=mat2gray(cx{1,1});
 %imshow(cx{1,2})
 
 imwrite(rx,['E:\NIT\DIP\dip data proj\char\car\glx\' num2str(i) '.jpg']);
end

%khandane karakterha.........mini database1...................

for i=1:1
 for j=1:8
 temp=imread(['E:\NIT\DIP\dip data proj\char\car\glx\' num2str(j) '.jpg']);
 temp=im2bw(temp);
 nf1=temp.*cx{1,i};
 nf2=sum(sum(nf1));
 nf(j)=nf2/(sum(sum(temp)));
 mx=max(nf(j));
 
 
 if nf(1,1)== mx
 disp(1);
 else
 if nf(1,2)== mx
 disp(5);
 else
 if nf(1,3)== mx
 disp('j');
 else
 if nf(1,4)== mx
 disp(6);
 else
 if nf(1,5)== mx
 disp(3);
 else
 if nf(1,6)== mx
 disp(1);
 else
 if nf(1,7)== mx
 disp(7);
 else
 if nf(1,8)== mx
 disp(2);
 
 
 end
 end
 end
 end
 end
 end
 
 end
 
 end
 
 
 end
 
end

سپتامبر 16, 2019/3 دیدگاه /توسط admin

آشنایی با بینایی ماشین

بینایی ماشین (Machine Vision) و بینایی کامپیوتر

بینایی ماشین

اگر به طور خلاصه بخواهیم تعریفی از “بینایی ماشین” یا “Machine Vision” داشته باشیم ، به این صورت بیان می کنیم که : بینایی ماشین در واقع دادن قدرت دیدن به دستگاه ها و تجهیزات صنعتی با مجهز کردن آن ها به دوربین و کامپیوتر می باشد.

بینایی ماشین مجموعه ای از روش ها و تکنولوژی هاست که برای درک و آنالیز خودکار مبتنی بر تصاویر ، در زمینه هایی مثل بازرسی خودکار ، فرآیند کنترل و هدایت روبات در صنعت استفاده می شود. بینایی ماشین ارتباط نزدیکی با “بینایی رایانه ای ” دارد ولی با آن فرق دارد.

بینایی ماشین هم شامل طراحی یک راه حل برای فرایند است و هم مسائل فنی در حین فرایند است. از سال 2006 به بعد تا حدودی رابط کاربری استاندارد سازی شده است. اولین گام در بینایی ماشین ، دریافت یک تصویر است، که معمولا از دوربین ، لنز و نورپردازی استفاده می شود. بسته نرم افزاری بینایی ماشین از تکنیک های پردازش تصاویر دیجیتال برای استخراج اطلاعات لازم و تصمیم گیری برمبنای آن اطلاعات استفاده می کند.

تصویربرداری

معمولا از تصویر برداری دوبعدی در نورمرئی در بینایی ماشین استفاده می شود. البته جایگزین های دیگری مثل تصویربرداری در باند مادون قرمز ، تصویربرداری اسکن خط، تصویربرداری سه بعدی و تصویربرداری اشعه ایکس وجود دارد.

شکلی از تصویربرداری خطی و تصویر برداری سه بعدی

قسمت پردازش تصویر می تواند از وسیله تصویربرداری جدا باشد ، که در این صورت نیاز به یک رابط واسط نیاز است تا تصاویر را از دوربین دریافت کند(دریافت کننده فریم) و آن را برای انجام پردازش های بعدی به کامیپیوتر و سیستم پردازنده بدهد. اگر قسمت پردازش تصویر با دوربین ترکیب شده باشد ، اصطلاحا به آن دوربین هوشمند و یا سنسور هوشمند می گویند.

پردازش تصویر

بعد از دریافت تصویر نوبت به پردازش تصویر و استخراج اطلاعات از تصاویر می رسد. در پردازش تصویر اعمال مختلفی روی تصویر صورت میگیرد که شامل دو بخش بهبود تصاویر و استخراج ویژگی ها است. از جمله پردازش هایی که روی تصویر صورت می گیرد شامل : بازسازی و ترکیب تصاویر ، فیلتر کردن، آستانه گذاری ، شمارش پیکسل ، شناسایی لبه ، آنالیز رنگ ، شناسایی الگو ، و … است.

تصمیم گیری

در نهایت پس از دریافت و پردازش تصاویر و استخراج ویژگی و پارامترهای لازم نوبت به تصمیم گیری براساس این پارمترهای استخراج شده از تصویر می رسد.

چند مثال برای بینایی ماشین در زیر ذکر شده است :

بررسی وان حمام برای وجود خش
چک کردن اینکه آیا کیسه هو به درستی در اتومبیل نصب شده است یا نه
بررسی کاغذ هنگام تولید تا از نبود ایراد اطمینان حاصل شود
اطمینان از تولید درست سرنگ
پیدا کردن ناصافی در شیشه
هدایت روبات ها تا بتوانند با محیط ارتباط برقرار کنند

مزیت ها

فواید استفاده از یک سیستم بینایی ماشین چیست ؟

مهمترین فایده افزایش کیفیت محصول نهایی است . با اینکار نیازی به نمونه برداری از محصول نهایی و چک کردن نمونه نیست ، بلکه با بینایی ماشین می تواند صددرصد محصولات را بررسی کرد. برای نمونه در مثال تولید کاغذ ، هر اینج از کاغذ به دقت بررسی می شود و محصول نهایی دارای صددرصد کیفیت است. از دیگر مزیت ها می توان به افزایش سرعت ، دقت ، کاهش هزینه ها ، و انجام کارهایی که انسان قادر به انجام آن نیست ، اشاره کرد.

بینایی رایانه ای

بینایی رایانه ای یا “Computer Vision” یک فیلدی است که شامل دریافت ، پردازش ، آنالیز و فهم تصاویر است ؛ به طور کلی به دریافت تصاویر از محیط و استخراج اطلاعات کمی و کیفی از آن ها اطلاق می شود.

تشخیص چهره یا اثر انگشت ، خواندن پلاک اتومبیل و یا شمارش تعداد افراد از جمله کابردهای بینایی رایانه است.

مفاهیم بینایی رایانه ای بسیار نزدیک به بینایی ماشین است با این تفاوت که ،بینایی رایانه ای مفهوم کامل تری را در برمی گیرد و به طور کلی به پردازش و آنالیز تصاویر در دستگاه ها و اپلیکیشن های مختلف گفته می شود در صورتی که بینایی ماشین به صورت عملی و در محیط صنعتی صورت می گیرد.

در زیر جدولی ارائه شده است که تا حدودی تفاوت های بینایی رایانه ای با بینایی ماشین ذکر شده است :

منبع : http://d-i-p.ir

سپتامبر 11, 2019/0 دیدگاه /توسط daliri

رگرسیون لجستیک (LR)

آموزش عمومی پردازش تصویر و بینایی ماشین

رگرسیون لجستیک (Logistic regression) یک مدل آماری رگرسیون برای متغیرهای وابسته دوسویی مانند بیماری یا سلامت، مرگ یا زندگی است. این مدل را می‌توان به عنوان مدل خطی تعمیم‌یافته‌ای که از تابع لوجیت به عنوان تابع پیوند استفاده می‌کند و خطایش از توزیع چندجمله‌ای پیروی می‌کند، به‌حساب‌آورد. منظور از دو سویی بودن، رخ داد یک واقعه تصادفی در دو موقعیت ممکنه است. به عنوان مثال خرید یا عدم خرید، ثبت نام یا عدم ثبت نام، ورشکسته شدن یا ورشکسته نشدن و … متغیرهایی هستند که فقط دارای دو موقعیت هستند و مجموع احتمال هر یک آن‌ها در نهایت یک خواهد شد.

کاربرد این روش عمدتاً در ابتدای ظهور در مورد کاربردهای پزشکی برای احتمال وقوع یک بیماری مورد استفاده قرار می‌گرفت. لیکن امروزه در تمام زمینه‌های علمی کاربرد وسیعی یافته‌است. به عنوان مثال مدیر سازمانی می‌خواهد بداند در مشارکت یا عدم مشارکت کارمندان کدام متغیرها نقش پیش‌بینی دارند؟ مدیر تبلیغاتی می‌خواهد بداند در خرید یا عدم خرید یک محصول یا برند چه متغیرهایی مهم هستند؟ یک مرکز تحقیقات پزشکی می‌خواهد بداند در مبتلا شدن به بیماری عروق کرنری قلب چه متغیرهایی نقش پیش‌بینی‌کننده دارند؟ تا با اطلاع‌رسانی از احتمال وقوع کاسته شود.

رگرسیون لجستیک می‌تواند یک مورد خاص از مدل خطی عمومی و رگرسیون خطی دیده شود. مدل رگرسیون لجستیک، بر اساس فرض‌های کاملاً متفاوتی (دربارهٔ رابطه متغیرهای وابسته و مستقل) از رگرسیون خطی است. تفاوت مهم این دو مدل در دو ویژگی رگرسیون لجستیک می‌تواند دیده شود. اول توزیع شرطی $y|{\vec {x}}$ یک توزیع برنولی به جای یک توزیع گوسی است چونکه متغیر وابسته دودویی است. دوم مقادیر پیش‌بینی احتمالاتی است و محدود بین بازه صفر و یک و به کمک تابع توزیع لجستیک بدست می‌آید رگرسیون لجستیک احتمال خروجی پیش‌بینی می‌کند.

این مدل به صورت

$\operatorname {logit} (p)=\ln \left({\frac {p}{1-p}}\right)=\beta _{0}+\beta _{1}x_{1,i}+\cdots +\beta _{k}x_{k,i},$

$i=1,\dots ,n,\,$

است که

$p=\Pr(y_{i}=1).\,$

$p=\Pr(y_{i}=1|{\vec {x_{i}}};{\vec {\beta }})={\frac {e^{\beta _{0}+\beta _{1}x_{1,i}+\cdots +\beta _{k}x_{k,i}}}{1+e^{\beta _{0}+\beta _{1}x_{1,i}+\cdots +\beta _{k}x_{k,i}}}}={\frac {1}{1+e^{-\left(\beta _{0}+\beta _{1}x_{1,i}+\cdots +\beta _{k}x_{k,i}\right)}}}.$

برآورد پارامترهای بهینه

برای بدست آوردن پارامترهای بهینه یعنی ${\vec {\beta }}=[\beta _{0},\beta _{1},\cdots ,\beta _{k}]$ می‌توان از روش برآورد درست نمایی بیشینه (Maximum Likelihood Estimation) استفاده کرد. اگر فرض کنیم که تعداد مثال‌هایی که قرار است برای تخمین پارامترها استفاده کنیم $n$ است و این مثال‌ها را به این شکل نمایش دهیم $D=({\vec {x_{1}}},y_{1}),\cdots ({\vec {x_{n}}},y_{n})$ . پارامتر بهینه پارامتری است که برآورد درست نمایی را بیشینه کند، البته برای سادگی کار برآورد لگاریتم درست نمایی را بیشینه می‌کنیم. لگاریتم درست نمایی داده $D$ برای پارامتر ${\vec {\beta }}$ را با $L(D,{\vec {\beta }})$ نمایش می‌دهیم:

$L(D,{\vec {\beta }})=\log \left(\prod _{i=1}^{n}Pr(y_{i}=1|{\vec {x_{i}}};{\vec {\beta }})^{y_{i}}\times Pr(y_{i}=0|{\vec {x_{i}}};{\vec {\beta }})^{1-y_{i}}\right)=\sum _{i=1}^{n}y_{i}\times \log Pr(y_{i}=1|{\vec {x_{i}}};{\vec {\beta }})+(1-y_{i})\log Pr(y_{i}=0|{\vec {x_{i}}};{\vec {\beta }})$

اگر برای داده $i$ ام $y_{i}=1$ باشد، هدف افزایش $\Pr \left(y_{i}=1|{\vec {x_{i}}};{\vec {\beta }}\right)$ است و اگر $y_i$ صفر باشد هدف افزایش مقدار $\Pr \left(y_{i}=0|{\vec {x_{i}}};{\vec {\beta }}\right)$ است. از این رو از فرمول $Pr(y_{i}=1|{\vec {x_{i}}};{\vec {\beta }})^{y_{i}}\times Pr(y_{i}=0|{\vec {x_{i}}};{\vec {\beta }})^{1-y_{i}}$ استفاده می‌کنیم که اگر $y_{i}=1$ باشد، فرمول به ما $\Pr \left(y_{i}=1|{\vec {x_{i}}};{\vec {\beta }}\right)$ را بدهد و اگر $y_{i}=0$ بود به ما $\Pr \left(y_{i}=0|{\vec {x_{i}}};{\vec {\beta }}\right)$ را بدهد.

حال برای بدست آوردن پارامتر بهینه باید ${\vec {\beta }}$ یی پیدا کنیم که مقدار $L(D,{\vec {\beta }})$ را بیشینه کند. از آنجا که این تابع نسبت به ${\vec {\beta }}$ مقعر است حتماً یک بیشینه مطلق دارد. برای پیدا کردن جواب می‌توان از روش گرادیان افزایشی از نوع تصادفی اش استفاده کرد (Stochastic Gradient Ascent). در این روش هر بار یک مثال را به‌صورت اتفاقی از نمونه‌های داده انتخاب کرده، گرادیان درست نمایی را حساب می‌کنیم و کمی در جهت گرادیان پارامتر را حرکت می‌دهیم تا به یک پارامتر جدید برسیم. گرادیان جهت موضعی بیشترین افزایش را در تابع به ما نشان می‌دهد، برای همین در آن جهت کمی حرکت می‌کنیم تا به بیشترین افزایش موضعی تابع برسیم. اینکار را آنقدر ادامه می‌دهیم که گرادیان به اندازه کافی به صفر نزدیک شود. بجای اینکه داده‌ها را به‌صورت تصادفی انتخاب کنیم می‌توانیم به ترتیب داده شماره $1$ تا داده شماره $n$ را انتخاب کنیم و بعد دوباره به داده اولی برگردیم و این کار را به‌صورت متناوب چندین بار انجام دهیم تا به اندازه کافی گرادیان به صفر نزدیک شود. از لحاظ ریاضی این کار را می‌توان به شکل پایین انجام داد، پارامتر ${\vec {\beta }}$ را در ابتدا به‌صورت تصادفی مقدار دهی می‌کنیم و بعد برای داده $i$ ام و تمامی $j$ ‌ها، یعنی از $j=1$ تا $j=m+1$ تغییر پایین را اعمال می‌کنیم، دراینجا $\alpha$ همان مقداریست که در جهت گرادیان هربار حرکت می‌کنیم و $\left(y_{i}-{\frac {1}{1+e^{-\left(\beta _{0}+\beta _{1}x_{1,i}+\cdots +\beta _{k}x_{k,i}\right)}}}\right){\vec {x_{i,j}}}$ مشتق جزئی داده $i$ ام در بُعد $j$ ام است:

${\begin{cases}{\mbox{Initialize}}\,\,{\vec {\beta ^{\,old}}}\,\,{\mbox{randomly}}\\{\mbox{loop until convergence :}}\\\,\,{\mbox{for}}\,\,\,\,i=0\,\,\,\,{\mbox{to}}\,\,\,\,n:\\\,\,\,\,\,\,{\mbox{for}}\,\,\,\,j=0\,\,\,\,{\mbox{to}}\,\,\,\,m:\\\,\,\,\,\,\,\,\,\,\,\,\,{\vec {\beta _{j}^{\,new}}}={\vec {\beta _{j}^{\,old}}}+\alpha \left(y_{i}-{\frac {1}{1+e^{-\left(\beta _{0}^{\,old}+\beta _{1}^{\,old}x_{1,i}+\cdots +\beta _{k}^{\,old}x_{k,i}\right)}}}\right){\vec {x_{i,j}}}\\\,\,\,\,\,\,\beta ^{\,old}=\beta ^{\,new}\end{cases}}$

تنظیم مدل (Regularization)

پیچیدگی مدل‌های پارامتری با تعداد پارامترهای مدل و مقادیر آن‌ها سنجیده می‌شود. هرچه این پیچیدگی بیشتر باشد خطر بیش‌برازش (Overfitting) برای مدل بیشتر است. پدیده بیش‌برازش زمانی رخ می‌دهد که مدل بجای یادگیری الگوهای داده، داده را را حفظ کند و در عمل، فرایند یادگیری به خوبی انجام نمی‌شود. برای جلوگیری از بیش‌برازش در مدل‌های خطی مانند رگرسیون خطی یا رگرسیون لجستیک جریمه‌ای به تابع هزینه اضافه می‌شود تا از افزایش زیاد پارامترها جلوگیری شود. تابع هزینه را در رگرسیون لجستیک با منفی لگاریتم درست‌نمایی تعریف می‌کنیم تا کمینه کردن آن به بیشینه کردن تابع درست نمایی بیانجامد. به این کار تنظیم مدل یا Regularization گفته می‌شود. دو راه متداول تنظیم مدل‌های خطی روش‌های $L_{1}$ و $L_{2}$ هستند. در روش $L_{1}$ ضریبی از نُرمِ $L_{1}$ به تابع هزینه اضافه می‌شود و در روش $L_{2}$ ضریبی از نُرمِ $L_{2}$ که همان نُرمِ اقلیدسی است به تابع هزینه اضافه می‌شود.

در تنظیم مدل به روش $L_{1}$ تابع هزینه را به این شکل تغییر می‌دهیم:

$L_{r}(D,{\vec {\beta }})=-L(D,{\vec {\beta }})+\lambda ||{\vec {\beta }}||_{1}=-\sum _{i=1}^{n}y_{i}\times \log Pr(y_{i}=1|{\vec {x_{i}}};{\vec {\beta }})+(1-y_{i})\log Pr(y_{i}=0|{\vec {x_{i}}};{\vec {\beta }})+\lambda \sum _{k=0}^{m}|\beta _{k}|$

این روش تنظیم مدل که به روش لاسو (Lasso) نیز شهرت دارد باعث می‌شود که بسیاری از پارامترهای مدل نهائی صفر شوند و مدل به اصطلاح خلوت (Sparse) شود.

در تنظیم مدل به روش $L_{2}$ تابع هزینه را به این شکل تغییر می‌دهیم:

$L_{r}(D,{\vec {\beta }})=L(D,{\vec {\beta }})+\lambda ||{\vec {\beta }}||_{2}^{2}=-\sum _{i=1}^{n}y_{i}\times \log Pr(y_{i}=1|{\vec {x_{i}}};{\vec {\beta }})+(1-y_{i})\log Pr(y_{i}=0|{\vec {x_{i}}};{\vec {\beta }})+\lambda \sum _{k=0}^{m}\beta _{k}^{2}$

در روش تنظیم از طریق $L_{2}$ سعی می‌شود طول اقلیدسی بردار ${\vec {\beta }}$ کوتاه نگه داشته شود. $\lambda$ در روش $L_{1}$ و $L_{2}$ یک عدد مثبت است که میزان تنظیم مدل را معین می‌کند. هرچقدر $\lambda$ کوچکتر باشد جریمه کمتری برا بزرگی نرم بردار پارامترها یعنی ${\vec {\beta }}$ پرداخت می‌کنیم. مقدار ایدئال $\lambda$ از طریق آزمایش بر روی داده اعتبار (Validation Data) پیدا می‌شود.

تفسیر احتمالی تنظیم مدل

اگر بجای روش درست نمایی بیشینه از روش بیشینه سازی احتمال پسین استفاده کنیم به ساختار «تنظیم مدل» یا همان regularization خواهیم رسید. اگر مجموعه داده را با $D$ نمایش بدهیم و پارامتری که به دنبال تخمین آن هستیم را با ${\vec {\beta }}$ ، احتمال پسین $Pr\left({\vec {\beta }}\,|\,D\right)$ ، طبق قانون بیز متناسب خواهد بود با حاصلضرب درست نمایی یعنی $Pr\left(D\,|\,{\vec {\beta }}\right)$ و احتمال پیشین یعنی $Pr\left({\vec {\beta }}\right)$ :

$Pr\left({\vec {\beta }}\,|\,D\right)={\frac {Pr\left(D\,|\,{\vec {\beta }}\right)\times Pr\left({\vec {\beta }}\right)}{Pr\left(D\right)}}$

ازین رو

$argmax_{\vec {\beta }}Pr\left({\vec {\beta }}\,|\,D\right)=argmax_{\vec {\beta }}{\frac {Pr\left(D\,|\,{\vec {\beta }}\right)\times Pr\left({\vec {\beta }}\right)}{Pr\left(D\right)}}=argmax_{\vec {\beta }}Pr\left(D\,|\,{\vec {\beta }}\right)\times Pr\left({\vec {\beta }}\right)$

معادله خط پیشین نشان می‌دهد که برای یافتن پارامتر بهینه فقط کافیست که احتمال پیشین را نیز در معادله دخیل کنیم. اگر احتمال پیشین را یک توزیع احتمال با میانگین صفر و کوواریانس $\tau ^{2}I$ در نظر بگیریم به معادله پایین می‌رسیم:

$argmax_{\vec {\beta }}\,\,\log Pr\left(D\,|\,{\vec {\beta }}\right)=argmax_{\vec {\beta }}\,\,\log \prod _{i=1}^{n}Pr(y_{i}|{\vec {x_{i}}}\,\,;{\vec {\beta }})Pr\left({\vec {\beta }}\right)=argmax_{\vec {\beta }}\,\,\log \left(\prod _{i=1}^{n}Pr(y_{i}=1|{\vec {x_{i}}};{\vec {\beta }})^{y_{i}}\times Pr(y_{i}=0|{\vec {x_{i}}};{\vec {\beta }})^{1-y_{i}}{\frac {1}{{\sqrt {2\pi }}\tau }}exp\left({\frac {-||{\vec {\beta }}||^{2}}{2\tau }}\right)\right)$

با ساده کردن این معادله به نتیجه پایین می‌رسیم:

$argmax_{\vec {\beta }}\,\,\log Pr\left(D\,|\,{\vec {\beta }}\right)=argmax_{\vec {\beta }}\sum _{i=1}^{n}y_{i}\times \log Pr(y_{i}=1|{\vec {x_{i}}};{\vec {\beta }})+(1-y_{i})\log Pr(y_{i}=0|{\vec {x_{i}}};{\vec {\beta }})-{\frac {1}{2\tau ^{2}}}||{\vec {\beta }}||^{2}-\log {\sqrt {2\pi }}\tau$

با تغییر علامت معادله، بیشینه‌سازی را به کمینه‌سازی تغییر می‌دهیم، $\lambda$ در این معادله همان ${\frac {1}{2\tau ^{2}}}$ است:

$argmax_{\vec {\beta }}\,\,\log Pr\left(D\,|\,{\vec {\beta }}\right)=argmin_{\vec {\beta }}-\left(\sum _{i=1}^{n}y_{i}\times \log Pr(y_{i}=1|{\vec {x_{i}}};{\vec {\beta }})+(1-y_{i})\log Pr(y_{i}=0|{\vec {x_{i}}};{\vec {\beta }})\right)+\lambda ||{\vec {\beta }}||^{2}$

همان‌طور که دیدیم جواب همان تنظیم مدل با نرم $L_{2}$ است.

حال اگر توزیع پیشین را از نوع توزیع لاپلاس با میانگین صفر در نظر بگیریم به تنظیم مدل با نرم $L_{1}$ خواهیم رسید.

از آنجا که میانگین هر دو توزیع پیشین صفر است، پیش‌فرض تخمین پارامتر بر این بنا شده‌است که اندازه پارامتر مورد نظر کوچک و به صفر نزدیک باشد و این پیش‌فرض با روند تنظیم مدل همخوانی دارد.

منبع

رگرسیون لوژستیک (لجستیک)

زمانی که متغیر وابسته ی ما دو وجهی (دو سطحی مانند جنسیت، بیماری یا عدم بیماری و …) است و می خواهیم از طریق ترکیبی از متغیرهای پیش بین دست به پیش بینی بزنیم باید از رگرسیون لجستیک استفاده کنیم. چند مثال از کاربردهای رگرسیون لجستیک در زیر ارائه می گردد.

1. در فرایند همه گیر شناسی ما می خواهیم ببینیم آیا یک فرد بیمار است یا خیر. اگر به عنوان مثال بیماری مورد نظر بیماری قلبی باشد پیش بینی کننده ها عبارتند از سن، وزن، فشار خون سیستولیک، تعداد سیگارهای کشیده شده و سطح کلسترول.

2. در بازاریابی ممکن است بخواهیم بدانیم آیا افراد یک ماشین جدیدی را می خرند یا خیر. در اینجا متغیرهایی مانند درآمد سالانه، مقدار پول رهن، تعداد وابسته ها، متغیرهای پیش بین می باشند.

3. در تعلیم و تربیت فرض کنید می خواهیم بدانیم یک فرد در امتحان نمره می آورد یا خیر.

4. در روانشناسی می خواهیم بدانیم آیا فرد یک رفتار بهنجار اجتماعی دارد یا خیر.

در تمام موارد گفته شده متغیر وابسته یک متغیر دو حالتی است که دو ارزش دارد. زمانی که متغیر وابسته دو حالتی است مسایل خاصی مطرح می شود.

1. خطا دارای توزیع نرمال نیست. 2. واریانس خطا ثابت نیست. 3. محدودیت های زیادی در تابع پاسخ وجود دارد. مشکل سوم مطرح شده مشکل جدی تری است.

می توان از روش حداقل مجذورات وزنی برای حل مشکل مربوط به واریانس های نابرابر خطا استفاده نمود. بعلاوه زمانی که حجم نمونه بالا باشد می توان روش حداقل مجذورات برآوردگرهایی را ارائه می دهد که به طور مجانبی و تحت موقعیت های نسبتا عمومی نرمال می باشند. ما در رگرسیون لجستیک به طور مستقیم احتمال وقوع یک رخداد را محاسبه می کنیم. چرا که فقط دو حالت ممکن برای متغیر وابسته ی ما وجود دارد.

دو مساله ی مهم که باید در ارتباط با رگرسیون لجستیک در نظر داشته باشیم عبارتند از:

1. رابطه ی بین پیش بینی کننده ها و متغیر وابسته غیر خطی است.

2. ضرایب رگرسیونی از طریق روش ماکزیمم درستنمایی برآورد می شود.

رگرسیون لجستیک از لحاظ محاسبات آماری شبیه رگرسیون چند گانه است اما از لحاظ کارکرد مانند تحلیل تشخیصی می باشد. در این روش عضویت گروهی بر اساس مجموعه ای از متغییرهای پیش بین انجام می شود دقیقا مانند تحلیل تشخیصی. مزیت عمده ای که تحلیل لجستیک نسبت به تحلیل تشخیصی دارد این است که در این روش با انواع متغیرها به کار می رود و بنابراین بسیاری از مفروضات در مورد داده ها را به کار ندارد. در حقیقت آنچه در رگرسیون لجستیک پیش بینی می شود یک احتمال است که ارزش آن بین 0 تا 1 در تغییر است. ضرایب رگرسیونی مربوط به معادله ی رگرسیون لجستیک اطلاعاتی را راجع به شانس هر مورد خاص برای تعلق به گروه صفر یا یک ارائه می دهد. شانس به صورت احتمال موفقیت در برابر شکست تعریف می شود. ولی بدلیل ناقرینگی و امکان وجود مقادیر بی نهایت برای آن تبدیل به لگاریتم شانس می شود. هر یک از وزن ها را می توان از طریق مقدار خی دو که به آماره ی والد مشهور است به لحاظ معناداری آزمود. لگاریتم شانس، شانسی را که یک متغییر به طور موفقیت آمیزی عضویت گروهی را برای هر مورد معین پیش بینی می کند را نشان می دهد.

به طور کلی در روش رگرسیون لجستیک رابطه ی بین احتمال تعلق به گروه 1 و ترکیب خطی متغیرهای پیش بین بر اساس توزیع سیگمودال تعریف می شود. برای دستیابی به معادله ی رگرسیونی و قدرت پیش بینی باید به نحوی بتوان رابطه ای بین متغیرهای پیش بین و وابسته تعریف نمود. برای حل این مشکل از نسبت احتمال تعلق به گروه یک به احتمال تعلق به گروه صفر استفاده می شود. به این نسبت شانس OR گویند. به خاطر مشکلات شانس از لگاریتم شانس استفاده می شود. لگاریتم شانس با متغیرهای پیش بینی کننده ارتباط خطی دارد. بنابراین ضرایب بدست آمده برای آن باید بر اساس رابطه ی خطی که با لگاریتم شانس دارند تفسیر گردند. بنابراین اگر بخواهیم تفسیر را بر اساس احتمال تعلق به گروهها انجام دهیم باید لگاریتم شانس را به شانس و شانس را به اجزای زیر بنایی آن که احتمال تعلق است تبدیل نماییم. آماره ی والد که از توزیع خی دو پیروی می کند نیز برای بررسی معناداری ضرایب استفاده می شود. از آزمون هاسمر و لمشو نیز برای بررسی تطابق داده ها با مدل استفاده می شود معنادار نبودن این آزمون که در واقع نوعی خی دو است به معنای عدم تفاوت داده ها با مدل یعنی برازش داده با مدل است.

رگرسیون چند متغیری: در این رگرسیون هدف این است که از طریق مجموعه ای از متغیرهای پیش بین به پیش بینی چند متغیر وابسته پرداخته شود در واقع اتفاقی که در رگرسیون کانونی می افتد.

رگرسیون لجستیک (LOGESTIC REGRESSION)

همان طور که می‌دانیم در رگرسیون خطی، متغیر وابسته یک متغیر کمی در سطح فاصله‌ای یا نسبی است و پیش‌ بینی کننده‌ ها از نوع متغیرهای پیوسته، گسسته یا ترکیبی از این دو هستند. اما هنگامی که متغیر وابسته در کمی نباشد، یعنی به صورت دو یا چندمقوله‌ای باشد، از رگرسیون لجستیک استفاده می‌کنیم که امکان پیش‌بینی عضویت گروهی را فراهم میکند. این روش موازی روشهای تحلیل تشخیصی و تحلیل لگاریتمی است. برای مثال، پیش بینی مرگ و میر نوزادان بر اساس جنسیت نوزاد، دوقلو بودن و سن و تحصیلات مادر.

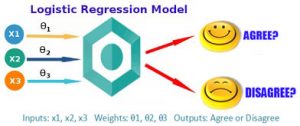
بسیاری از مطالعات پژوهشی در علوم اجتماعی و علوم رفتاری، متغیرهای وابسته از نوع دو مقوله ای را بررسی میکنند. مانند: رأی دادن یا ندادن در انتخابات، مالکیت (مثلاٌ داشتن یا نداشتن کامپیوتر شخصی) و سطح تحصیلات (مانند: داشتن یا نداشتن تحصیلات دانشگاهی) ارزیابی میشود. از جمله حالت های پاسخ دوتایی عبارتند از: موافق- مخالف، موفقیت – شکست، حاضر – غایب و جانبداری – عدم جانبداری.

متغیرهای تحلیل رگرسیون لجستیک

در تحلیل رگرسیون لجستیک، همیشه یک متغیر وابسته و معمولا مجموعه ای از متغیرهای مستقل وجود دارند که ممکن است دو مقوله ای، کمی یا ترکیبی از آن ها باشند. به علاوه لازم نیست متغیرهای دو مقوله ای به طور واقعی دوتایی باشند. به عنوان مثال ممکن است پژوهشگران متغیر وابسته کمی دارای کجی شدید را به یک متغیر دومقوله ای که در هر طبقه آن تعداد موردها تقریباً مساوی است تبدیل کنند. مانند آن چه که در مورد رگرسیون چندگانه دیدیم، برخی از متغیرهای مستقل در رگرسیون لجستیک می توانند به عنوان متغیرهای همپراش (covariates) مورد استفاده قرار گیرند تا پژوهشگران بتوانند با ثابت نگه داشتن یا کنترل آماری این متغیرها اثرات دیگر متغیرهای مستقل را بهتر ارزیابی کنند.

پیش فرض های رگرسیون لجستیک

با این که رگرسیون لجستیک در مقایسه با رگرسیون خطی پیش فرض های کمتری دارد (به عنوان مثال پیش فرض های همگنی واریانس و نرمال بودن خطاها وجود ندارد)، رگرسیون لجستیک نیازمند موارد زیر است:

هم خطی چندگانه کامل وجود نداشته باشد.
خطاهای خاص نباید وجود داشته باشد (یعنی، همه متغیرهای پیش بین مرتبط وارد شوند و پیش بین های نامربوط کنار گذاشته شوند).
متغیرهای مستقل باید در مقیاس پاسخ تراکمی یا جمع پذیر (cumulative response scale)، فاصله ای یا سطح نسبی اندازه گیری شده باشند (هر چند که متغیرهای دو مقوله ای نیز می توانند مورد استفاده قرار گیرند).

برای تفسیر درست نتایج، رگرسیون لجستیک در مقایسه با رگرسیون خطی نیازمند نمونه های بزرگتری است. با این که آماردان ها در خصوص شرایط دقیق نمونه توافق ندارند. بسیاری پیشنهاد می کنند تعداد افراد نمونه حداقل باید ۳۰ برابر تعداد پارامترهایی باشند که برآورد می شوند.

منبع

رگرسیون لجستیک چیست؟

رگرسیون لجستیک، شبیه رگرسیون خطی است با این تفاوت که نحوه محاسبه ضرایب در این دو روش یکسان نمی باشد. بدین معنی که رگرسیون لجستیک، به جای حداقل کردن مجذور خطاها (کاری که رگرسیون خطی انجام می دهد)، احتمالی را که یک واقعه رخ می دهد، حداکثر می کند. همچنین، در تحلیل رگرسیون خطی، برای آزمون برازش مدل و معنی داربودن اثر هر متغیر در مدل، به ترتیب از آماره های Fوt استفاده می شود، در حالی که در رگرسیون لجستیک، از آماره های کای اسکوئر(X₂) و والد استفاده می شود (مومنی، ۱۳۸۶: ۱۵۸).

رگرسیون لجستیک نسبت به تحلیل تشخیصی نیز ارجحیت دارد و مهم ترین دلیل آن است که در تحلیل تشخیصی گاهی اوقات احتمال وقوع یک پدیده خارج از طیف(۰) تا (۱) قرار می گیرد و متغیرهای پیش بین نیز باید دارای توزیع در داخل محدوده (۰) تا (۱) قرار دارد و رعایت پیش فرض نرمال بودن متغیرهای پیش بینی لازم نیست (سرمد، ۱۳۸۴: ۳۳۱).

انواع رگرسیون لجستیک

همان طور که در ابتدای مبحث تحلیل رگرسیون لجستیک گفته شد، در رگرسیون لجستیک، متغیر وابسته می تواند به دو شکل دووجهی و چندوجهی باشد. به همین خاطر، در نرم افزارSPSS شاهد وجود دو نوع تحلیل رگرسیون لجستیک هستیم که بسته به تعداد مقولات و طبقات متغیر وابسته، می توانیم از یکی از این دو شکل استفاده کنیم:

۱-رگرسیون لجستیک اسمی دووجهی: موقعی است که متغیر وابسته در سطح اسمی دووجهی (دوشقی) است. یعنی در زمانی که با متغیر وابسته اسمی دووجهی سروکار داریم.

۲-رگرسیون لجستیک اسمی چندوجهی : موقعی مورد استفاده قرار می گیرد که متغیر وابسته، اسمی چندوجهی (چندشقی) است.

منبع

سپتامبر 6, 2019/0 دیدگاه /توسط daliri

مشخصات فنی دوربین پلاک‌خوان معاینه فنی

وبلاگ

مشخصات فنی دوربین های پلاک‌خوان جهت نصب در مراکز خدمات فنی مجاز اتحادیه کشوری سوخت های جایگزین و خدمات وابسته، به شرح زیر اعلام شد.

جهت خریداری توجه داشته باشید، دوربین مورد نظر شرایط فنی زیر را دارا باشد.

مشخصات فنی دوربین های پلاک‌خوان مراکز معاینه فنی
1/2.8 cmos – 2 mp Full HD	Image sensor
Color: 0/1 lox – B/w: 0/1 lox	Min illumination
1s~1/10,000s	Minshutter time
P-Iris	Auto Iris
IR cut filter with auto switch	Day & Night
DNR	Digital noise reduction
True – 120 dB Real	Wide dynamic range
H.264-MPEG4-MJPEG	Video compression
UP TO 1920*1080	Resolution
UP TO 30 fps at (1920*1080)	Frame Rate
-30 °C ~ 55 °C – Humidity 100%	Operating conditions
At least one zone configurable	Rol
Yes	HLC
Yes	BLC
Yes	Defog
Yes	ELC
Yes	Smart Focus
Yes	Network Interface
User Authentication, anonymous access	Security
ONVIF (Profile S, Profile G)	System Compatibility
PoE	Power Supply
Import/Export configuration capability – rese buttom – web broeser access	Other feature
Varifocal P-Iris	Lens Type
Under the terms of Iris	Focal Length
IP66	Housing

منبع

آگوست 23, 2019/2 دیدگاه /توسط BehsanAndish

ماشین تورینگ چیست ؟ قسمت 1

آموزش های عمومی هوش مصنوعی

ماشین‌تورینگ

ماشین تورینگ (به انگلیسی: Turing machine) یک دستگاه فرضی است که روی نشان‌های روی یک قطعه نوار بر اساس جدول قوانین دست‌کاری انجام می‌دهد. با وجود اینکه مکانیزم ماشین تورینگ مقدماتی است، مفهومش برای پوشش عملکردهای بسیار پیچیده کافی و گسترده‌است. ماشین تورینگ می‌تواند برای شبیه‌سازی هر الگوریتم کامپیوتری و توضیح نحوه عملکرد یک واحد پردازشگر مرکزی به کار آید. حافظه این ماشین ساختاری بسیار ساده دارد. یعنی می‌تواند بصورت یک آرایه یک بعدی از عناصر (سلولها) باشد که هر یک می‌توانند حافظ تنها یک نماد باشند. این آرایه از هر دو طرف باز و نامحدود است (حافظه بینهایت) و اطلاعات آن می‌توانند به هر ترتیبی فراخوانی شوند.

نمایش هنری یک ماشین تورینگ

ماشین‌های تورینگ
ماشین محاسبه تورینگ ماشین تورینگ متناوب ماشین تورینگ کوانتومی ماشین تورینگ غیرقطعی ماشین خواندنی تورینگ ماشین راستگرد خواندنی تورینگ ماشین تورینگ احتمالی ماشین تورینگ چندمسیره ماشین‌های هم‌ارز با ماشین تورینگ

تاریخچه

زمینه‌های تاریخی:ماشین محاسباتی

معرفی ماشین تورینگ توسط دانشمند انگلیسی آلن تورینگ در سال ۱۹۳۶ میلادی، گام دیگری را در مسیر ایجاد و پیدایش ماشین‌های محاسباتی حالات متناهی به نمایش می‌گذارد. رابین گندی یکی از دانشجویان آلن تورینگ و دوست صمیمی تمام عمرش، ریشه‌های نظریه ماشین محاسباتی بابیج(۱۸۳۴) را کاوش کرد و در حقیقت نظریه بابیج را دوباره ارائه کرد:

آنالیز گندی در مورد ماشین تحلیلی بابیج پنج عملیات زیر را توضیح می‌دهد:

۱-عملگرهای ریاضی + و – و *

۲-هر ترتیبی از عملگرها قابل قبول است

۳-تکرار عملگر

۴-تکرار شرطی

۵-انتقال شرطی

تعریف منطقی (انتزاع ذهنی مفاهیم کلی)

ماشین تورینگ عبارت است از یک پنج-تاپل (پنج‌تایی) به‌صورت $M=(Q,\Sigma ,\Gamma ,\delta ,q_{0})\!$ ، که در اینجا:

$M\!$ برای نمایش مفهوم ماشین انتخاب شده است.
$Q\!$ مجموعه‌ای است متناهی، از حالات داخلی.
$\Gamma \!$ مجموعه‌ای متناهی موسوم به الفبای نوار و حاوی نمادی مخصوص $B\!$ برای نمایش یک فاصلهٔ خالی روی نوار ماشین است.
$\Sigma \!$ زیرمجموعه‌ای است از $\Gamma -\{B\}\!$ و موسوم به الفبای ورودی. یعنی الفبای ورودی زیر مجموعه‌ای از الفبای نوار است که شامل خالی نیست. نوارهای خالی نمی‌توانند بعنوان ورودی استفاده شوند.
$\delta \!$ عبارت است از یک تابع جزئی، موسوم به تابع انتقال از دامنهٔ $Q\times \Gamma \!$ به برد $Q\times \Gamma \times \{L,R\}\!$ .
$q_{0}\!$ حالت شروع نام دارد، یعنی، حالتی از ماشین است که محاسبه را درآن آغاز می‌کنیم.

بطور کلی $\delta \!$ یک تابع جزئی روی $Q\!\times \Gamma \!$ است و تفسیرش عملکرد ماشین تورینگ را بیان می‌کند.

تعریف وصفی (عملی دنیای خارج از ذهن)

ماشین تورینگ به صورت ریاضی، ماشینی است که روی یک نوار عمل می‌کند. روی این نوار، نمادهایی است که ماشین هم می‌تواند بخواند و هم می‌تواند بنویسد و همزمان از آنها استفاده می‌کند. این عمل به طور کامل با یک سری دستورالعمل ساده و محدود تعریف شده است. ماشین تورینگ از موارد زیر تشکیل شده است:

۱. یک نوار، به سلولهایی تقسیم‌بندی شده است و هر سلول شامل نمادهایی است. الفبا شامل نماد تهی خاصی و یک یا تعداد دیگری نماد است. فرض می‌شود که این نوار خودسرانه به چپ و راست رسانده شود. ماشین تورینگ از نوارهایی تأمین می‌شود که برای محاسبه لازم است.

۲. یک کلاهک وجود دارد که قادر به خواندن و نوشتن نمادهایی است که روی نوار قرار گرفته‌اند و بطور همزمان نوار را به سمت چپ و راست یکی از (و تنها یک) سلولها حرکت می‌دهد. در بضی مدلها، کلاهک حرکت می‌کند و نوار ثابت می‌ماند.

۳. یک دستگاه ثبت حالت وجود دارد که حالت‌های ماشین تورینگ را ذخیره می‌کند (یکی از تعداد زیادی حالت متناهی). یک حالت شروع وجود دارد که همراه با مقدار دهی اولیه است. این حالت‌ها، حالت ذهن شخصی را که محاسبات را انجام می‌دهد، جایگزین می‌کنند.

۴. یک جدول محدود (که گاهی جدول عمل یا تابع انتقال نامیده می‌شود)، از دستورالعمل‌ها وجود دارد که در حال حاضر، حالت (q_i) و نماد (a_j) به ماشین داده می‌شود (برای مدل‌های ۵تایی و گاهی ۴تایی) که روی نوار خوانده می‌شود و می‌گوید که ماشین، این موارد را به تزتیب زیر برای مدلهای ۵تایی انجام دهد:

یا پاک کردن یا نوشتن یک نماد (بصورت جایگزین کردن a_i با a_j۱)
حرکت کردن کلاهک نوار (که توسط d_k مشخص می‌شود و می‌تواند مقادیر L برای حرکت به چپ و R برای حرکت به سمت راست به خود بگیرد. همچنین مقدار N نشان دهنده ساکن بودن نوار است).
فرض کنید یک حالت مشابه یا یک حالت جدید مشخص شده است (رفتن به وضعیت q_i۱)

در مدل‌های ۴تایی پاک کردن یا نوشتن یک نماد (a_j۱) و حرکت کلاهک نوار به سمت چپ یا راست (d_k) بصورت دستورالعمل‌های جداگانه مشخص شده‌اند. بطور خاص، جدول به ماشین می‌گوید که چیزی را پاک کند یا یک نماد را بنویسد (ia) یا کلاهک نوار به سمت چپ و راست حرکت کند (ib). فرض کنید که حالتهای مشابه یا حالتهای جدیدی مشخص شده‌اند. اما عملیات‌های (ia) و (ib) دستورالعمل‌های یکسانی ندارند. در برخی از مدلها، اگر در جدول، ورودی از نمادها و حالتها نداشته باشیم، ماشین متوقف خواهد شد. سایر مدلها، نیاز به همه ورودی‌ها دارند تا پر شوند. توجه داشته باشید که هر بخش از ماشین- حالتها و نمادها، مجموعه‌ها، اقدامات، چاپ کردن، پاک کردن و حرکت نوار- محدود، گسسته و تشخیص پذیر است. این، پتانسیل نامحدود نوارهاست که خود مقدار نامحدودی از یک فضای ذخیره‌سازی است.

مقایسه با ماشین‌های واقعی

اغلب گفته می‌شود که ماشین تورینگ، بر خلاف ماشین‌های اتومات، به اندازه ماشین‌های واقعی قدرتمند هستند و قادر به انجام هر عملیاتی که ماشین واقعی می‌تواند بکند هستند. چیزی که در این مطلب جا ماند این است که یک ماشین واقعی تنها می‌تواند در بسیاری از تنظیمات متناهی باشد؛ در واقع ماشین واقعی چیزی نیست جز یک ماشین اتوماتیک محدود خطی. از طرف دیگر ماشین تورینگ با ماشین‌هایی که دارای ظرفیت حافظه‌های نامحدود محاسباتی هستند، معادل است. از نظر تاریخی رایانه‌هایی که محاسبات را در حافظه داخلی شان انجام می‌دادند، بعدها توسعه داده شده‌اند.

چرا ماشین‌های تورینگ مدل‌های مناسبی برای رایانه‌های واقعی هستند؟

۱. هرچیزی که ماشین واقعی می‌تواند محاسبه کند، ماشین تورینگ هم می‌تواند. برای مثال ماشین تورینگ، می‌تواند هرچیز طبق روالی که در زبان‌های برنامه‌نویسی پیدا می‌شود شبیه‌سازی کند. همچنین می‌تواند فرایندهای بازگشتی و هریک از پارامترهای مکانیسم شناخته شده را شبیه‌سازی کند.

۲. تفاوت، تنها در قابلیت ماشین تورینگ برای دخالت در مقدار محدودی اطلاعات نهفته است؛ بنابراین، ماشین تورینگ می‌تواند در مدت زمان محدودی، در اطلاعات دخالت داشته باشد.

۳. ماشین واقعی همانند ماشین‌های تورینگ می‌توانند حافظه مورد نیازش را به کمک دیسک‌های بیشتر، بزرگ کند. اما حقیقت این است که هم ماشین تورینگ و هم ماشین واقعی، برای محاسبات نیازی به فضا در حافظه‌شان ندارند.

۴. شرح برنامه‌های ماشین واقعی که از مدل ساده‌تر انتزاعی استفاده می‌کنند، پیچیده‌تر از شرح برنامه‌های ماشین تورینگ است.

۵. ماشین تورینگ الگوریتم‌های مستقل را که چقدر از حافظه استفاده می‌کنند، توصیف می‌کند. در دارایی حافظه همهٔ ماشین‌ها، محدودیتی وجود دارد؛ ولی این محدودیت می‌تواند خود سرانه در طول زمان افزایش یابد.

ماشین تورینگ به ما اجازه می‌دهد دربارهٔ الگوریتم‌هایی که برای همیشه نگه داشته می‌شوند، توصیفاتی ارائه دهیم؛ بدون در نظر گرفتن پیش رفت در معماری محاسبات با ماشین معمولی.

۶. ماشین تورینگ جملات الگوریتم را ساده می‌کند. الگوریتم‌های در حال اجرا در ماشین آلات انتزاعی معادل تورینگ، معمولاً نسبت به همتایان خود که در ماشین‌های واقعی در حال اجرا هستند عمومی ترند. زیرا آنها دارای دقت دلخواه در انواع اطلاعات قابل دسترس هستند و هیچوقت با شرایط غیرمنتظره روبرو نمی‌شوند. یکی از نقطه ضعف‌های ماشین تورینگ این است که برنامه‌های واقعی که نوشته می‌شوند ورودی‌های نامحدودی را در طول زمان دریافت می‌کنند؛ در نتیجه هرگز متوقف نمی‌شوند.

محدودیت‌های ماشین تورینگ

نظریه پیچیدگی محاسباتی

یکی از محدودیت‌هاو معایب ماشین‌های تورینگ این است که آنها توانایی چیدمان خوب را ندارند. برای مثال کامپیوترهای برنامه‌ای با ذخیره مدرن، نمونه‌هایی از یک مدل خاص ماشین انتزاعی که به نام ماشین برنامه دسترسی رندم یا مدل ماشین RASP می‌باشند.

همزمانی

یکی دیگر از محدودیت‌های ماشین تورینگ این است که همزمانی را خوب ارئه نمی‌دهد. برای مثال برای اندازه عدد صحیحی که می‌تواند توسط «متوقف کننده غیر قطعی دایمی» محاسبه شود، محدودیت وجود دارد. ماشین تورینگ روی یک نوار خالی شروع می‌کند. در مقابل، ماشین‌های «همیشه متوقف» همزمان هستند که بدون ورودی می‌توانند عدد صحیح نامتناهی را محاسبه کنند.

منبع

ایده ماشین تورینگ چگونه مطرح شد و چه چیزی را دنبال می‌کرد؟

بخش اول

ماشین تورینگ! مفهومی که به اندازه فرد مطرح کننده خود از اهمیت ویژه‌ای برخوردار است و نقش مهمی در رسیدن علوم کامپیوتر و همچنین فناوری محاسبات به مقطع کنونی دارد. اگرچه به سادگی می‌توان بدون داشتن اطلاعاتی حتی جزئی در رابطه با ماشین تورینگ، به خوبی از نحوه کارکرد كامپيوترها و سازوكار محاسبات در ماشین‌ها مطلع شد اما در این حالت، قطعاً کلید اصلی مسئله در نظر گرفته نشده است. درک ماشین تورینگ، درک روح محاسبات ماشینی و شناخت تولد و تکامل ماشین‌های محاسبه‌گر است. اما به راستی، تورینگ چگونه و با چه هدفی چنین ایده‌ای را مطرح کرد؟

سرآغاز

تاریخچه محاسبات دیجیتال به دو بخش عهد عتیق و عهد جدید قابل تقسیم است. پیشوایان عهد قدیم به سرپرستی لایبنیتز (Gottfreid Wilhelm Leibniz) در سال 1670 میلادی منطق مورد نیاز ماشین‌های محاسباتی دیجیتال را فراهم کرده و پیشروان عهد جدید به سرپرستی فون نویمان (John von Neumann) در سال 1940 خود این ماشین‌ها را ساختند. آلن تورینگ، که در سال 1912 متولد شده است، جایی در میان این دو عصر مهم قرار گرفته و شاید بتوان وی را به نوعی پیوند دهنده این دو عهد مهم به شمار آورد. وی در سال 1936، درست در زمانی که به تازگی از کالج کینگ در دانشگاه کمبریج فارغ‌التحصیل شده و به دانشگاه پرینستون در نیوجرسی امریکا رفته بود، با نگارش و انتشار مقاله‌ای با عنوان «درباره اعداد رایانش‌پذیر، ‌با کاربردی بر مسئله تصمیم‌گیری» (On Computable Numbers, with an application to the Entscheidungs problem )، راهنمای پیاده‌سازی ماشین‌های با منطق ریاضی شد.

در این مقاله، تورینگ قصد داشت تا مسئله Entscheidungs problem ریاضی‌دان آلمانی، دیوید هیلبرت (David Hilbert) را که در سال 1928 طرح کرده بود، حل کند. موضوع نهایی مسئله فوق، تصمیم‌گیری درباره این بود که آیا یک روال مکانیکی می‌تواند صحت یک عبارت منطقی را در تعداد محدودی حرکت تعیین کند یا خیر؟ تورینگ در این مقاله، ایده و تصور رایج در دهه 1930 از یک کامپیوتر (یک شخص مجهز به یک مداد، کاغذ و دستورالعمل‌های مشخص) را در نظر گرفته و با حذف تمام رگه‌های هوشمندی (Intelligence) از آن به غیر از امکان پیروی از دستورالعمل‌ها و امکان خواندن و نوشتن علامت‌هایی از یک الفبای خاص روی یک رول کاغذ با طول بی نهایت، ماشینی را معرفی کرد که بعدها به ماشین تورینگ معروف شد و سرآغاز طلوع ماشین‌های محاسباتی دیجیتال امروزی شد.

ماشین تورینگ، یک جعبه سیاه ریاضیاتی بود که از یک سری دستورالعمل از پیش تعیین شده پیروی می‌کرد. این دستورالعمل‌ها با استفاده از علامت‌هايي مشخص که روی کاغذ یا نوع خاصی از حافظه نوشته می‌شد به ماشین تحویل داده می‌شد. این ماشین می‌توانست در هر لحظه، یک علامت را از روی یک خانه خوانده، نوشته یا پاک کند و خانه مذکور را که یک واحد کوچک موجود روی رول کاغذ است به سمت چپ یا راست هدایت کند. علامت‌های پیچیده می‌توانند به‌صورت دنباله‌ای از علامت‌های ساده‌تر پیاده‌سازی شوند و در این حالت، پیچیدگی احتمالی، تشخیص تفاوت بین دو علامت مختلف و وجود یا نبود فاصله‌های خالی روی نوار است. «بیت»های اطلاعاتی در این ماشین می‌توانند دو فرم مختلف داشته باشند: الگوهایی در فضا که در طول زمان ارسال می‌شوند و حافظه مدت‌دار خوانده می‌شوند یا الگوهایی در زمان که در فضا ارسال شده و کد نامیده می‌شوند. در ماشین تورینگ، زمان به‌صورت رشته‌ای از اتفاقات یکسان نیست، بلکه به صورت دنباله‌ای از تغییر حالات در ماشین مذکور قابل تصور خواهد بود.

ایده ماشین‌های بدون قطعیتِ پیشگو، به اساس کار هوش نزدیک‌تر بود؛ شهود و بینش، پر‌کننده فاصله میان عبارات منطقی است.

در ادامه مقاله، تورینگ امکان وجود ماشین منفردی را مطرح کرد که می‌تواند هر توالی محاسباتی‌ را محاسبه کند. «چنین ماشین محاسباتی جامعی می‌تواند رفتار هر ماشین دیگری را با استفاده از شرح کار کد شده آن تقلید کند.» بنابراین، با ذکر این عبارت، تورینگ ایده «نرم‌افزار» را در حدود 76 سال قبل پیشگویی کرده بود. در پایان، تورینگ مسئله پیچیده هیلبرت را به روشی جالب پاسخ داده است. او عبارتی را یافته بود که در تعداد گام‌های محاسباتی محدود، توسط هیچ ماشینی قابل محاسبه نبود: آیا شرح کار کد شده یک ماشین که توسط ماشین محاسباتی جامع تورینگ اجرا می‌شود، در نهایت به پایان می‌رسد یا برای همیشه اجرا می‌شود؟

بر همین اساس، وی پاسخ مسئلهEntscheidungs problem را منفی دانسته و از این طریق، پايه‌گذار طراحی ماشین‌های محاسباتی دیجیتال شد. در سال 1949، فون‌نویمان در یک سخنرانی با اشاره به این مفهوم مطرح شده توسط تورینگ عنوان کرد: «شما می‌توانید چیزی بسازید که کاری را که می‌شود انجام داد، انجام دهد. اما نمی‌توانید نمونه‌ای بسازید که به شما بگوید که آیا آن کار انجام‌پذیر است یا خیر؟»
تورینگ با درک محدودیت‌های ماشین‌های با قطعیت مشخص، شروع به جست‌وجو در زمینه محاسبات غیر‌قطعی با ماشین‌های پیشگو کرد. از نظر او، این نوع ماشین‌ها، همان روال گام به گام را مورد استفاده قرار می‌دهند اما با استفاده از نوعی پیشگویی، گاهی جهش‌هایی غیرقابل پیش‌بینی نیز انجام می‌دهند.

رمزگشایی

پس از پایان تحصیلات در دوره دکترا، تورینگ در سال 1938 به انگلیس بازگشت و گسترش جنگ جهانی دوم منجر به بروز نیاز هرچه بیشتر به ایده‌های وی شد. به همین دلیل، وی در مدرسه رمز و کدهای محرمانه دولت به خدمت گرفته شد. در آنجا، تورینگ و همکارانش به همراه استادش، ماکسول نیومن (Maxwell Newman) ارتباطات دشمن را، از جمله پیام‌های کدگذاری شده توسط ماشین آلمانی انيگما، رمزگشایی کردند. انیگما، ماشینی شبیه به ماشین تورینگ بود که امکان کد‌گذاری متن ورودی خود را با مکانیزمی مکانیکی فراهم می‌کرد. آن‌ها کار کدگشایی رمزهای انیگما را با مجموعه‌ای از دستگاه‌های الکترومکانیکی که بمب (bombe) نامیده می‌شدند، شروع کردند که هر کدام می‌توانست در هر لحظه 36 حالت احتمالی پیکربندی انیگما را شبیه‌سازی کند.

از این طریق، آن‌ها توانستند با همکاری افرادی دیگر، کامپیوتری بسیار پیچیده و دیجیتال با نام Clossus بسازند که از یک حافظه داخلی ساخته شده با 1500 لامپ خلاء بهره می‌برد که وضعیت حافظه برنامه‌پذیری را برای جست‌وجوی کدها فراهم می‌کرد. این مدل بعدها با نسل دوم خود با 2400 لامپ خلاء جایگزین شد که علاوه بر تأثیر اساسی بر نتیجه جنگ، تحولی شگرف در تکامل رایانه‌های دیجیتال به شمار می‌آمد. اسرار مربوط به ساخت این ماشین برای حدود 30 سال از طرف سازمان‌های اطلاعاتی انگلیس به‌صورت محرمانه نگه‌داری می‌شد.

پس از پایان جنگ، نیاز به کامپیوترهای پیشرفته‌تر، از کاربردهای رمزگشایی به سمت طراحی بمب‌های اتمی پیش رفت. در سال 1946 ایالات‌متحده با داشتن کامپیوتر زمان جنگ خود، یعنی ENIAC (سرنام Electronic Numerical Integrator and Computer)، کار روی طراحی سلاح‌های اتمی را در پیش گرفت. در انستیتو مطالعات پیشرفته پرینستون و با حمایت مالی ارتش ایالات‌متحده، دفتر تحقیقات نیروی دریایی و همچنین کمیسیون انرژی اتمی امریکا، فون‌نویمان موظف شد تا نمونه الکترونیکی ماشین جامع تورینگ را بسازد. در آن زمان، هدف او ساخت ماشین تورینگی بود که حافظه آن با سرعت نور قابل دسترسی بوده و به پردازش در زمینه‌های مختلف می‌پرداخت. اما هدف دولت ایالات متحده امریکا از سرمایه‌گذاری روی چنین ماشینی تعیین امکان ساخت بمب هیدروژنی بود و به همین دلیل، فون نویمان قول داد که ماشین مذکور که از 5 کیلوبایت فضای ذخیره‌سازی بهره می‌برد، امکان اجرای کدهای داینامیک مذکور را داشته باشد.

بعدها، طراحی کامپیوتر مذکور در اختیار همگان گذارده شد و آي‌بي‌ام آن را تجاری کرد. در نخستین جلسه هماهنگی برای اجرای پروژه مذکور در سال 1945، فون نویمان اعلام کرد که قصد دارد پیاده‌سازی دستورات را نیز همانند اعداد در حافظه انجام دهد و این ترکیب داده‌ها و دستورالعمل‌ها کاملاً بر‌اساس مدل تورینگ بود.

ماشین تورینگ چیست ؟ قسمت 1
ماشین تورینگ چیست ؟ قسمت 2
ماشین تورینگ چیست ؟ قسمت 3

ژانویه 18, 2018/1 دیدگاه/توسط daliri

بایگانی برچسب برای: hk

خوانش پلاک خودرو از تصاویر جاده‌ای

(پیاده سازی شده برای پلاک های ایرانی)

سورس برنامه در نرم افزار متلب:

بینایی ماشین

تصویربرداری

پردازش تصویر

تصمیم گیری

مزیت ها

بینایی رایانه ای

برآورد پارامترهای بهینه

تنظیم مدل (Regularization)

تفسیر احتمالی تنظیم مدل

رگرسیون لوژستیک (لجستیک)

رگرسیون لجستیک (LOGESTIC REGRESSION)

متغیرهای تحلیل رگرسیون لجستیک

پیش فرض های رگرسیون لجستیک

رگرسیون لجستیک چیست؟

انواع رگرسیون لجستیک

ماشین‌های تورینگ

تاریخچه

تعریف منطقی (انتزاع ذهنی مفاهیم کلی)

تعریف وصفی (عملی دنیای خارج از ذهن)

مقایسه با ماشین‌های واقعی

چرا ماشین‌های تورینگ مدل‌های مناسبی برای رایانه‌های واقعی هستند؟

محدودیت‌های ماشین تورینگ

نظریه پیچیدگی محاسباتی

همزمانی

ایده ماشین تورینگ چگونه مطرح شد و چه چیزی را دنبال می‌کرد؟

سرآغاز

ایده ماشین‌های بدون قطعیتِ پیشگو، به اساس کار هوش نزدیک‌تر بود؛ شهود و بینش، پر‌کننده فاصله میان عبارات منطقی است.

رمزگشایی

تلفن های تماس:

ساعات کاری

پیوند ها :

محصولات :