بایگانی‌های مرتبه مدل مارکوف

کاربردهای مدل مخفی مارکوف

بازشناسی گفتار
ترجمه ماشینی
پیش‌بینی ژن
هم‌ترازسازی توالی
تشخیص فعالیت
تاشدگی پروتئین
تشخیص چهره

تاریخچه

مدل مخفی مارکوف برای اولین بار در مجموعه‌مقالات آماری leonard E.Baum و سایر نویسندگان در نیمه دوم دهه ۱۹۶۰ توضیح داده شد. یکی از اولین کاربردهای HMM تشخیص گفتار بوده که در اواسط دههٔ ۱۹۷۰ شروع شد. HMM در نیمهٔ دوم ۱۹۸۰ وارد حوزهٔ آنالیز دنباله‌های بیولوژیکی، به‌طور خاص DNA شد. از آن پس، کاربرد آن در بیوانفورماتیک گسترش یافت.

انواع مدل مخفی مارکوف

مدل پنهان مارکوف می‌تواند فرایندهای پیچیده مارکوف را که حالتها بر اساس توزیع احتمالی مشاهدات را نتیجه می‌دهند، مدل کند. به‌طور مثال اگر توزیع احتمال گوسین باشد در چنین مدل مارکوف پنهان خروجی حالتها نیز از توزیع گوسین تبعیت می‌کنند. علاوه بر این مدل مخفی مارکوف می‌تواند رفتارهای پیچیده‌تر را نیز مدل کند. جایی که خروجی حالت‌ها از ترکیب دو یا چند توزیع گوسین پیروی کند که در این حالت احتمال تولید یک مشاهده از حاصلضرب گوسین انتخاب شدهٔ اولی در احتمال تولید مشاهده از گوسین دیگر به دست می‌آید.

فرایند مارکوف گسسته

یک سیستم مانند شکل زیر را که در هر لحظه در یکی از حالت متمایز S1,… ,SN است در نظر بگیرید. در زمان‌های گسسته و با فواصل منظم، حالت سیستم با توجه به مجموعه‌ای از احتمالات تغییر می‌کند. برای زمان‌های… ,t=۱٬۲ حالت در لحظه t را با qt نشان می‌دهیم. برای یک توصیف مناسب از سیستم فعلی نیاز به دانستن حالت فعلی در کنار تمام حالات قبلی می‌باشد. برای یک حالت خاص از زنجیره مارکوف مرتبه اول، توصیف احتمالاتی تنها با حالت فعلی و حالت قبلی مشخص می‌شود.

\ P(q_{t}=S_{j}|q_{t-1}=S_{i},q_{t-2}=S_{k},...)=

\ P(q_{t}=S_{j}|q_{t-1}=S_{i})

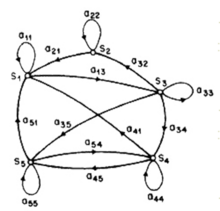
حال تنها فرایندهایی را در نظر می‌گیریم که در آن‌ها سمت راست رابطه فوق مستقل از زمان است و به همین دلیل ما مجموعه‌ای از احتمالات انتقال بین حالت‌ها را خواهیم داشت.

$\ a_{ij}=P(q_{t}=S_{j}|q_{t-1}=S_{i})\qquad i\geq 1,N\geq j$

که در آن احتمال انتقال بین حالات دارای خواص زیر است.

$a_{ij}\geq 0$

$\sum _{j=1}^{N}a_{ij}=1$

فرایند تصادفی فوق را مدل مارکوف قابل مشاهده می‌گویند زیرا خروجی مدل مجموعه‌ای از حالات است که قرار گرفتن در آن‌ها متناظر با یک مشاهده می‌باشد. ما می‌توانیم دنباله مشاهدات مورد انتظار خود را تولید کنیم و احتمال وقوع آن در زنجیره مارکوف را محاسبه نماییم. برای مثال با داشتن دنباله مشاهدات $\ O={q_{1},...,q_{t}}$ احتمال وقوع آن به صورت زیر بیان می‌شود.

$\ P(O|Model)=P({q_{1},q_{2},...,q_{2}}|Model)$

$\ P(q_{1}).P(q_{2}|q_{1}).P(q_{3}|q_{2})...P(q_{t}|q_{t-1})$

یکی دیگر از مواردی که مطرح می‌شود این است که اگر سیستم در حالت $\ q_{i}$ باشد با چه احتمالی به حالت $\ q_{j}$ می‌رود و با چه احتمالی در همان حالت $\ q_{i}$ باقی می‌ماند.

مرتبه مدل مارکوف

۱- مدل مارکوف مرتبه صفر

یک مدل مارکوف از مرتبه صفر هیچ حافظه‌ای ندارد و برای هر t و t’ در دنباله سمبل‌ها، $\ pr(X_{t}=S_{i})=pr(X_{t'}=S_{i})$ خواهد بود. مدل مارکوف از مرتبه صفر مانند یک توزیع احتمال چند جمله‌ای می‌باشد.

۲- مدل مارکوف مرتبه اول

یک مدل مارکوف مرتبه اول دارای حافظه‌ای با طول ۱ می‌باشد. توزیع احتمال در این مدل به صورت زیر مشخص می‌شود.

$\ pr(X_{t}=S_{i}|X_{t-1}=S_{j}),fori=1..k,j=1..k$

تعریف فوق مانند این است که k مدل مارکوف در مرتبه صفر برای هر $\ S_{j}$ داشته باشیم.

۳- مدل مارکوف مرتبه m ام

مرتبه یک مدل مارکوف برابر است با طول حافظه‌ای که مقادیر احتمال ممکن برای حالت بعدی به کمک آن محاسبه می‌شود. برای مثال، حالت بعدی در یک مدل مارکوف از درجه ۲ (مدل مارکوف مرتبه دوم) به دو حالت قبلی آن بستگی دارد.

مثال ۱: برای مثال اگر یک سکه معیوب A داشته باشیم که احتمالات شیر یا خط آمدن برای آن یکسان نباشد، می‌توان آن را با یک مدل مارکوف درجه صفر با استفاده از احتمالات (pr(H و (pr(H توصیف نمود.

pr(H)=0.6, pr(T)=۰٫۴

مثال ۲: حال فرض کنید که سه سکه با شرایط فوق در اختیار داریم. سکه‌ها را با اسامی B, A و C نام‌گذاری می‌نماییم. آنگاه برای توصیف روال زیر به یک مدل مارکوف مرتبه اول نیاز داریم:

فرض کنید سکه X یکی از سکه‌های A یا B باشد.
مراحل زیر را تکرار می‌کنیم.

a) سکه X را پرتاب می‌کنیم و نتیجه را می‌نویسیم.

b) سکه C را نیز پرتاب می‌کنیم.

c) اگر سکه C خط آمد، آنگاه سکه X را تغییر می‌دهیم (A را با B یا B را با A جایگزین می‌کنیم) و در غیر این صورت تغییری در سکه‌ها نمی‌دهیم.

انجام روال فوق مدل مارکوف مرتبه اول زیر را نتیجه خواهد داد.

یک پردازش مارکوفی مانند نمونه فوق در طول پیمایش احتمالات، یک خروجی نیز خواهد داشت. یک خروجی نمونه برای پردازش فوق می‌تواند به شکل HTHHTHHttthtttHHTHHHHtthtthttht باشد.

مدل مارکوف فوق را می‌توان به صورت نموداری از حالات و انتقال‌ها نیز نشان داد. کاملاً مشخص است که این‌گونه بازنمایی از مدل مارکوف مانند بازنمایی یک ماشین انتقال حالت محدود است که هر انتقال با یک احتمال همراه می‌باشد

مدل مخفی مارکوف (HMM)

تا اینجا ما مدل مارکوف، که در آن هر حالت متناظر با یک رویداد قابل مشاهده بود را معرفی نمودیم. در این بخش تعریف فوق را گسترش می‌دهیم، به این صورت که در آن، مشاهدات توابع احتمالاتی از حالتها هستند. در این صورت مدل حاصل یک مدل تصادفی با یک فرایند تصادفی زیرین است که پنهان است و تنها توسط مجموعه‌ای از فرایندهای تصادفی که دنباله مشاهدات را تولید می‌کنند قابل مشاهده است.

برای مثال فرض کنید که شما در یک اتاق هستید و در اتاق مجاور آن فرد دیگری سکه‌هایی را به هوا پرتاب می‌کند و بدون اینکه به شما بگوید این کار را چگونه انجام می‌دهد و تنها نتایج را به اطلاع شما می‌رساند. در این حالت شما با فرایند پنهان انداختن سکه‌ها و با دنباله‌ای از مشاهدات شیر یا خط مواجه هستید. مسئله‌ای که اینجا مطرح می‌شود چگونگی ساختن مدل مارکوف به منظور بیان این فرایند تصادفی است. برای مثال اگر تنها مشاهدات حاصل از انداختن یک سکه باشد، می‌توان با یک مدل دو حالته مسئله را بررسی نمود. یک مدل مخفی مارکوف را می‌توان با تعیین پارامترهای زیر ایجاد نمود:

تعداد حالات ممکن: تعداد حالتها در موفقیت مدل نقش به سزایی دارد و در یک مدل مخفی مارکوف هر حالت با یک رویداد متناظر است. برای اتصال حالتها روش‌های متفاوتی وجود دارد که در عمومی‌ترین شکل تمام حالتها به یکدیگر متصل می‌شوند و از یکدیگر قابل دسترسی می‌باشند. تعداد مشاهدات در هر حالت: تعداد مشاهدات برابر است با تعداد خروجیهایی که سیستم مدل شده خواهد داشت.

N تعداد حالتهای مدل M تعداد سمبلهای مشاهده در الفبا، اگر مشاهدات گسسته باشند آنگاه M یک مقدار نا محدود خواهد داشت.

$\ A={a_{ij}}$

$\ A=[a_{ij}]$ ماتریس انتقال حالت:یک مجموعه از احتمالات در بین حالت‌ها

$\ a_{ij}=p(q_{t+1}=j|q_{t}=i),\qquad i\geq 1,N\geq j$

که در آن $\ q_{t}$ بیانگر حالت فعلی می‌باشد. احتمالات انتقال باید محدودیتها طبیعی یک توزیع احتمال تصادفی را برآورده نمایند. این محدودیتها شامل موارد زیر می‌گردند

$\ a_{ij}\geq 0,\qquad i\geq 1,N\geq j$

$\sum _{j=1}^{N}a_{ij}=1,\qquad 1\leq i\leq N$

برای حالات مدل ارگودیک برای تمامi وjها مقدار $\ a_{ij}$ بزرگتر از صفر است و در موردی که اتصالی بین حالات وجود ندارد $\ a_{ij}=0$ است.

توزیع احتمال مشاهدات: یک توزیع احتمال برای هر یک از حالتها

$\ B={b_{j}(k)}$

$\ b_{j}(k)=p{o_{t}=v_{k}|q_{t}=j},\qquad 1\leq j\leq N,\qquad 1\leq k\leq M$

که در آن $\ v_{k}$ بیانگرkامین سمبل مشاهده شده در الفبا است و $\ o_{t}$ بیانگر بردار پارامترهای ورودی فعلی می‌باشد. در مورد مقادیر احتمال حالتها نیز شرایط موجود در نظریه احتمال باید رعایت گردند.

$\ b_{j}(k)\qquad 1\leq j\leq N,\qquad 1\leq K\leq M$

$\sum _{K=1}^{M}b_{j}(k)=1,\qquad 1\leq j\leq N$

اگر مشاهدات به صورت پیوسته باشند، باید به جای احتمالهای گسسته از یک تابع چگالی احتمال پیوسته استفاده شود. معمولاً چگالی احتمال به کمک یک مجموع وزندار از M توزیع نرمال μ تخمین زده می‌شود.

$\ b_{j}(o_{t})=\Sigma _{m=1}^{M}c_{jm}\mu (\mu _{jm},\Sigma _{jm},o_{t})$

که در آن $\ \mu _{jm}$ ، $\ C_{jm}$ , $\ \Sigma _{jm}$ , به ترتیب ضریب بردار میانگین، ضریب وزندهی و ماتریس کواریانس می‌باشند. در رابطه فوق مقادیر $\ c_{jm}$ باید شرایط زیر را ارضا نماید: