بایگانی‌های ماشین تورینگ

بایگانی برچسب برای: ماشین تورینگ

برنامه نویسی Asynchronous

برنامه نویسی Asynchronous – آشنایی با Process ها، Thread ها و AppDomain ها

در طول یکسری مطالب آموزشی قصد داریم تا مبحث برنامه نویسی Asynchronous و Thread ها در زبان سی شارپ آشنا شویم. فرض کنید برنامه ای نوشتید که قرار است اطلاعات 500 هزار نفر را پردازش و یک گزارش تولید کند. در صورتی که به صورت عادی اقدام به پیاده سازی این قابلیت کنیم، در طول پردازش این اطلاعات برنامه ما دیگر قابل استفاده نخواهد بود و مجبوریم صبر کنیم تا عملیات پردازش اطلاعات تمام شود یا بهتر است یک مثال دیگر بزنیم.

فرض کنید زمانی که در حال تماشای یک فیلم هستید دیگر امکان انجام کارهای دیگر، مثلاً تایپ در برنامه Word یا برنامه نویسی نباشد. اما هیچ گاه این مشکلات برای شما بوجود نمی آید، زیرا سیستم عامل ها به بهترین شکل عملیات هم زمانی را پیاده سازی کرده و به شما این اجازه را می دهند تا در آن واحد نسبت به انجام چندین عملیات اقدام کنید. در زبان سی شارپ نیز این امکان برنامه نویسان داده شده است تا نسبت به پیاده سازی عملیات ها به صورت همزمان اقدام کنند. برای اینکار باید از Thread ها استفاده کنیم که در طول چند مطلب قصد داریم با شیوه های مختلف استفاده از Thread ها آشنا شویم. اما قبل از شروع کد نویسی بهتر است که با یکسری مفاهیم اولیه آشنا شده و سپس به سراغ قابلیت ها برنامه نویسی Asynchronous در زبان سی شارپ برویم.

Process چیست؟

زمانی که کاربر برنامه ای را اجرا می کند مقداری از حافظه و همچنین منابع به این برنامه تخصیص داده می شوند. اما همانطور که گفتیم یکی از قابلیت های سیستم های عامل این است که می توان چندین برنامه را به صورت همزمان اجرا کرد. یکی از وظایف سیستم عامل تفکیک حافظه و منابع برای هر یک از برنامه های در حال اجرا است که این جدا سازی بوسیله Process ها انجام می شود.

در حقیقت هر Process مرزبندی بین برنامه های اجرا است برای جدا سازی منابع و حافظه های تخصیص داده شده. دقت کنید که لزوماً تعداد Process برابر با تعداد برنامه های در حال اجرا نیست، یک برنامه می تواند یک یا چند Process را در زمان اجرا درگیر کند. در سیستم عامل ویندوز می توان از بخش Task Manager لیست برنامه های در حال اجرا و Process ها را مشاهده کرد. در تصویر زیر لیست برنامه هایی که بر روی سیستم من در حال اجرا است را مشاهده می کنید:

در صورتی که بر روی دکمه More details کلیک کنید می توانید از تب Processes لیست Process های در حال اجرا را مشاهده کنید:

هر یک Process های در حال اجرا حافظه، منابع تخصیص داده شده و روند اجرای مربوط به خود را دارند. در تصویر بالا نیز مشخص است، برای مثال در زمان گرفتن عکس بالا، Prcess مربوط به برنامه paint.net مقدار 20.4% از CPU و همچنین 107.6MB از حافظه را اشغال کرده است. در اینجا بیشتر به بحث CPU Usage باید دقت کنیم که نشان دهنده میزان استفاده یک Process از CPU است. CPU Usage در حقیقت یک ترتیب اجرا است که اصطلاحاً به آن Thread می گویند. هر Process می تواند شامل یک یا چندین Thread باشد که هر Thread وظیفه انجام یک عملیات خاص را بر عهده دارد. اما زمان اجرای هر Process یک Thread اولیه اجرا می شود که به آن اصطلاحاً Main Thread گفته می شود.

Process های Multi-Thread

همانطور که گفتیم هر Process می تواند شامل یک یا چندین Thread باشد. این Thread ها تنها توسط Process ایجاد نمی شوند و افرادی که اقدام به ایجاد نرم افزار می کنند (همان برنامه نویس های معروف) نیز می توانند برای انجام عملیات های مورد نظر اقدام به ایجاد Thread کنند.

برای مثال محیط Visual Studio را در نظر بگیرید، این محیط در طول زمان نوشتن کدها عملیات های دیگری را نیز برای شما انجام می دهد، مانند پردازش سایر فایل های پروژه، رنگی کردن کدها، نمایش Intellisense و …، اما شما احساس می کنید که تمامی این کار به صورت همزمان انجام می شوند، به این دلیل که برای هر یک از این عملیات ها یک Thread جداگانه ایجاد می شود که تمامی این Thread ها در Prcess مربوط به Visual Studio در حال اجرا هستند و به همین دلیل شما نباید منتظر بمانید تا عملیات های در حال اجرا به اتمام برسند و می توانید کار خود را ادامه دهید.

Thread های در حال اجرا در یک Process نیاز به یکسری اطلاعات در مورد Process دارند تا بتوانند به کار خود ادامه دهند. به این اطلاعات اصطلاحاً Prcess Global Data یا داده های عمومی یک پراسس می گویند. اگر بخواهیم نمایی کلی از یک Process را نشان دهیم می توان شکل زیر را مثال زد:

تصویر بالا، یک Process را نشان می دهد که شامل دو Thread است، هر یک از این Thread ها یک وظیفه خاص را انجام می دهند، اما به سکری اطلاعات دسترسی دارند که به آن ها PGD یا Process Global Data می گویند.

تا اینجا با دو مفهوم Process و Thread آشنا شدیم، اما همانطور که گفتیم در زبان سی شارپ می توانیم Thread هایی ایجاد کنیم که هر Thread یک کار خاص را انجام می دهد. برای کار با Thread ها و برای شروع، با کلاسی به نام Thread که در فضای نام System.Threading قرار دارد کار می کنیم. به صورت زیر می توانیم یک thread جدید با استفاده از کلاس Thread ایجاد کرده و آنرا اجرا کنیم:

static void Main(string[] args)
{
    var thread1 = new Thread(Thread1Job);
    var thread2 = new Thread(Thread2Job);
    var thread3 = new Thread(Thread3Job);
    thread1.Start();
    thread2.Start();
    thread3.Start();
}

public static void Thread1Job()
{
    for (int counter = 0; counter &lt; 50; counter++)
    {
   Console.WriteLine("From thread1: " + counter);
    }
}

public static void Thread2Job()
{
    for (int counter = 0; counter &lt; 50; counter++)
    {
        Console.WriteLine("From thread2: " + counter);
    }
}

public static void Thread3Job()
{
    for (int counter = 0; counter &lt; 50; counter++)
    {
        Console.WriteLine("From thread3: " + counter);
    }
}

همانطور که مشاهده می کنید در کد بالا 3 شئ از نوع Thread ایجاد کردیم و برای پارامتر Constructor متد مورد نظر را ارسال کردیم. Constructor کلاس Thread پارامترش از نوع Delegate است و به همین دلیل می توان یک متد را جهت اجرا در Thread به عنوان پارامتر به آن ارسال کرد. بعد از تعریف thread ها به ترتیب آن را بوسیله متد Start اجرا می کنیم. در تصویر زیر خروجی کد بالا را مشاهده می کنید که کد های Thread ها به صورت همزمان اجرا شدند:

اگر در کد بالا متد ها را بدون استفاده از Thread ها فراخوانی می کردیم Thread2Job پس از اجرای Thread1Job اجرا شده و الی آخر. در این مطلب مقدمه ای بر مبحث Thread ها در زبان سی شارپ داشتیم. در مطالب بعدی با اصول اولیه و مکانیزم های مختلف استفاده از Thread ها و همچنین ریسک هایی که در زمان استفاده از Thread ها وجود دارد آشنا خواهیم شد.

منبع

قسمت اول آموزش-برنامه نویسی Asynchronous – آشنایی با Process ها، Thread ها و AppDomain ها

قسمت دوم آموزش- آشنایی با ماهیت Asynchronous در Delegate ها

قسمت سوم آموزش-آشنایی با فضای نام System.Threading و کلاس Thread

قسمت چهارم آموزش- آشنایی با Thread های Foreground و Background در دات نت

قسمت پنجم آموزش- آشنایی با مشکل Concurrency در برنامه های Multi-Threaded و راهکار های رفع این مشکل

قسمت ششم آموزش- آشنایی با کلاس Timer در زبان سی شارپ

قسمت هفتم آموزش-آشنایی با CLR ThreadPool در دات نت

قسمت هشتم آموزش- مقدمه ای بر Task Parallel Library و کلاس Parallel در دات نت

قسمت نهم آموزش- برنامه نویسی Parallel:آشنایی با کلاس Task در سی شارپ

قسمت دهم آموزش-برنامه نویسی Parallel در سی شارپ :: متوقف کردن Task ها در سی شارپ – کلاس CancellationToken

قسمت یازدهم آموزش- برنامه نویسی Parallel در سی شارپ :: کوئری های Parallel در LINQ

قسمت دوازدهم آموزش- آشنایی با کلمات کلیدی async و await در زبان سی شارپ

قسمت سیزدهم آموزش- استفاده از متد WhenAll برای اجرای چندین Task به صورت همزمان در سی شارپ

آوریل 4, 2020/0 دیدگاه /توسط daliri

ماشین تورینگ چیست ؟ قسمت 3

آموزش های عمومی هوش مصنوعی

آزمون تورینگ چیست و چه کاربردی دارد؟

به همین دلیل، از لحاظ منطق و معماری، بیشتر کامپیوترهای امروزی از نوادگان مستقیم ماشین تورینگی هستند که از تجهیزات به‌جا مانده از جنگ در ساختمانی واقع در مزرعه‌ای در نیوجرسی ساخته شده بود. تورینگ و فون نویمان نخستین‌بار یکدیگر را در سال 1935 در کمبریج ملاقات کردند و پس از آن به مدت دو سال در دانشگاه پرینستون در کنار یکدیگر بودند. جایی که نیومن برای مدت شش ماه به آن‌ها ملحق شد و در کنار یکدیگر به تحصیل و تبادل نظر پرداختند.

این‌که فن نویمان و تورینگ تا چه حد در زمان جنگ با یکدیگر همکاری داشته‌اند، چندان معلوم نيست، اما چیزی که مشخص است آن است که تورینگ از نوامبر 1942 تا مارس 1943 در امریکا حضور داشته است در حالی که فون نویمان از فوریه تا جولای 1943 در انگلیس بوده است. در طی جنگ، فیزیکدانان انگلیسی با همکاری فون نویمان، همکاری‌های بسیار مهمی را در پروژه بمب اتمی در Los Alamos در نیومکزیکو به انجام رساندند. در عین حال، تحلیل‌گران رمز امریکایی، در انجام تلاش‌های رمزگشایی انگلیس به همکاری با تورینگ پرداختند. با این‌که تورینگ، فون‌نویمان و نیومن نمی‌توانستند آزادانه با هم مکاتبه کنند اما شاید ایده‌هایشان را در خلال و پس از اتمام جنگ به‌صورت شفاهی با یکدیگر در میان گذاشته‌اند. مدل تورینگ یک مدل یک بعدی بود که رشته‌ای از علامت‌ها را روی یک نوار کاغذی در نظر می‌گرفت در حالی که پیاده‌سازی فون نویمان یک مدل دو بعدی به شمار می‌آمد؛ یک ماتریس با آدرس دسترسی تصادفی که در بیشتر کامپیوترهای امروزی نیز وجود دارد. اینترنت- مجموعه‌ای از ماشین‌های به هم پیوسته تورینگ که به یک نوار مشترک دسترسی دارند- چشم‌انداز مدل مربوطه را سه بعدی کرد و هنوز، روش کار کامپیوترها از سال 1946 تاکنون بی‌تغییر باقی مانده است.

درس گرفتن از اشتباهات

تورینگ و نویمان از وجود خطا در ماشین‌هایشان مطلع بودند. با این‌که کدهای آن زمان به سادگی قابل اشكال‌زدايي بودند، اما سخت‌افزار به شدت غیر‌قابل اطمینان بود و نتایجی بی‌ثبات ارائه می‌کرد. مشکلی که اکنون کاملاً برعکس شده است. هردوی آن‌ها می‌دانستند که سیستم‌های بیولوژیک روی متدهای آماری و مقاوم در برابر خطا برای پردازش متمرکز شده‌اند (سیستم‌هایی نظیر کدگذاری فرکانسی پالس‌ها در مغز) و فرض کردند که فناوری نیز باید از همین روند پیروی کند. به اعتقاد فون نویمان، اگر هر خطا گرفته شده، تبیین می‌شد و سپس تصحیح می‌شد، سیستمی به پیچیدگی ارگانیسم‌های زنده نمی‌توانستند پاسخ‌هایی در حد میلی‌ثانیه داشته باشند. به اعتقاد تورینگ نیز اگر باید ماشینی بی‌خطا باشد، پس نمی‌تواند هوشمند نیز باشد. وقتی تورینگ در سال 1948به گروه نیومن در دانشگاه منچستر که مشغول طراحی Manchester Mark 1 بودند پیوست، یک تولید‌کننده عدد تصادفی در آن گنجاند که اجازه می‌داد کامپیوتر حدس زده و از اشتباهات خود درس بگیرد. لازم به ذکر است که Manchester Mark 1، نمونه اولیه Ferranti Mark 1 بود که نخستین کامپیوتر دیجیتالی با برنامه ذخیره شده به شمار می‌آمد.

با این‌که ماشین جامع با قطعیت تورینگ بیشترین توجه‌ها را به سوی خود جلب کرد، ایده ماشین‌های بدون قطعیتِ پیشگوی وی به اساس کار هوش نزدیک‌تر بود؛ شهود و بینش، پر‌کننده فاصله میان عبارات منطقی است. ماشین‌های پیشگوی تورینگ امروزه دیگر مفاهیم مجرد نظري نیستند چراکه موتورهای جست‌وجوی اینترنت مثال خوبی از وجود آن‌ها به‌شمار مي‌آيند. یک موتور جست‌وجو در حالت عادی به‌صورت قطعیتی (deterministic) کار می‌کند تا زمانی که کاربری روی یک لینک کلیک می‌کند. از این طریق، کاربر به‌طور غیر‌قطعی (non-deterministic)، مکان اطلاعات سودمند و پر ارزش را به نقشه داده‌ای موتور جست‌وجو اضافه می‌کند.

تورینگ می‌خواست بداند که چگونه مولکول‌ها می‌توانستند به‌طور مجموعه‌ای خود را سازماندهی کرده یا این‌که آیا ماشین می‌تواند فکر کند یا خیر؟ فون نویمان می‌خواست بداند که مغز چگونه کار می‌کند و آیا ماشین‌ها می‌توانند خود را باز‌تولید‌کنند؟ تورینگ که در سن 41 سالگی در‌گذشت، یک نظريه ناتمام در زمینه Morphogenesis (تکوینِ ترکیب) از خود به‌جای گذاشت و فون نویمان نیز که در سن 53 سالگی درگذشت، یک تئوری ناتمام در زمینه خود بازتولیدی (مدلی که بر‌اساس برداشتی از توانایی ماشین تورینگ از تولید کپی‌هایی از خود شکل گرفته بود) از خود به‌جای گذارد. اگر هردوی آن‌ها مدت طولانی‌تری زنده می‌ماندند و ایده‌های آن دو با یکدیگر ترکیب می‌شد، نتایج جالب و شگفت‌انگیزی می‌توانست رقم بخورد. زندگی آن‌ها به فاصله بسیار کوتاهی از کشف مکانیزم درونی ترجمه بین توالی و ساختار در بیولوژی به اتمام رسید و اگر آن‌ها از این کشف مطلع می‌شدند، چه نوآوری‌های خارق‌العاده‌ای را می‌توانستند به ارمغان بیاورند!

بخش دوم

ماشین تورینگ

ماشین تورینگ دستگاهی است که بر‌اساس قواعدی که در یک جدول آورده شده، علامت‌های نوشته شده روی یک نوار کاغذی را خوانده و بر‌اساس توالی آن‌ها، محاسباتی را انجام می‌دهد. با وجود سادگی، این ماشین می‌تواند منطق هر الگوریتم کامپیوتری را شبیه‌سازی کرده و به طور خاص، یک مثال خوب در توضیح عملکرد پردازنده‌های مرکزی درون کامپیوترها به شمار می‌آید.

این ماشین نخستین‌بار توسط آلن تورینگ در سال 1936 و در قالب یک مقاله، در پاسخ به مسئله‌ای که ریاضیدان آلمانی، دیوید هیلبرت منتشر کرده بود، مطرح شد. مسئله هیلبرت تصمیم‌گیری درباره این بود که آیا یک روال مشخص وجود دارد که بتواند صحت یک عبارت منطقی را در مراحلی متناهی محاسبه کند یا خیر؟ وی برای پاسخگویی به این سؤال‌، چنین ماشینی را تصور کرد و در نهایت به پاسخ منفی برای مسئله هیلبرت دست یافت. در اکتبر همان سال، فردی به نام امیل پست (Emil Post) مقاله‌ای با عنوان «Finite combinatory processes – formulation 1» منتشر کرد که در آن به توضیح و تبیین نوعی ماشین پرداخته شده بود که می‌توان آن را نوع خاصی از ماشین تورینگ به شمار آورد. کار وی مستقل از تورینگ انجام شده بود با این تفاوت که ماشین پست از الفبای باینری استفاده می‌کرد و مفاهیم حافظه ماشین وی حالت مجرد‌تری نسبت به تصورات تورینگ داشت. به همین جهت، گاهی به این چنین ماشین‌هایی پست-تورینگ (Post-Turing Machines) نیز گفته می‌شود. بر این اساس، باید توجه داشت که ماشین تورینگ یک فناوری محاسباتی عملی به شمار نمی‌آید بلکه یک دستگاه مجازی و نظری برای نمایش یک ماشین محاسباتی است. ماشین تورینگ، مثال خوبی برای دانشمندان کامپیوتر در زمینه درک کامل محدودیت‌های محاسبات مکانیکی است.

در اصل، ماشین تورینگ برای مدل‌سازی کامپیوتر کاربرد ندارد، بلکه هدف اصلی آن‌ مدل‌سازی خود مفهوم محاسبات است.

تورینگ بعدها و در سال 1948 در مقاله‌ای با عنوان ساز و كار رايانش (Computing Machinery and Intelligent)، تعریف دقیق‌تری از ماشین خودکار محاسباتی خود ارائه کرد و نام آن را ماشین محاسبات منطقی گذارد. وی در این مقاله چنین می‌گوید:

«… یک ظرفیت بی‌نهایت حافظه که به‌صورت نواری کاغذی با طول بی‌نهایت و تقسیم شده به مربع‌های مساوی که روی هر‌کدام امکان نوشتن علامت‌هایی وجود دارد. در هر لحظه، یک علامت در ماشین قرار می‌گیرد که علامت اسکن شده نامیده می‌شود. ماشین می‌تواند علامت مذکور را تغییر داده و در اصل، رفتار آن برگرفته از همان علامت است و دیگر علامت‌های موجود روی نوار نمی‌توانند تأثیری روی عملکرد ماشین بگذارند. نوار کاغذی می‌تواند به عقب و جلو حرکت کرده و این یکی از اصول اولیه کاری ماشین خواهد بود…»

ماشین تورینگ در اصل تشکیل یافته از چند عنصر اصلی است که عبارتند از:

نوار: که به بخش‌های کوچک مربع شکلی به نام سلول تقسیم شده و هرکدام می‌تواند حاوی یک علامت از یک الفبای محدود باشد. این نوار به طور دلخواه از سمت چپ یا راست نامتناهی بوده و توسط ماشین به راحتی جابه‌جا می‌شود. در بعضی از مدل‌ها، سمت چپ نوار با علامتی مشخص نشانه‌گذاری شده و نوار تنها به سمت راست نامتناهی در نظر گرفته می‌شود.

هد (Head): که برای خواندن و نوشتن علامت‌های روی نوار و انجام عملیات انتقال نوار به چپ یا راست مورد استفاده قرار می‌گیرد. در برخی مدل‌ها هد متحرک بوده و نوار ثابت است.
جدول متناهی دستورالعمل‌ها: که در برخی مواقع جدول عملکرد یا تابع گذار نامیده می‌شود، جدولی حاوی دستورالعمل‌هایی پنجگانه یا چهارگانه با فرمت qiaj→qi1aj1dk است که وظیفه تعیین عملکرد ماشین در برابر علامت‌های روی نوار را بر عهده دارد. متغیرهای آورده شده در عبارت بالا، نشان‌دهنده حالت جاری ماشین، علامت خوانده‌شده، میزان جابه‌جایی هد و… هستند.

ثبات حالت: حالت ماشین تورینگ را که از میان تعداد متناهی حالت مختلف انتخاب می‌شود، ذخیره می‌کند. همیشه یک حالت اولیه برای ماشین در زمان راه‌اندازی در این رجیستر ذخیره می‌شود. تورینگ معتقد بود که این رجیستر، جایگزین حالت ذهنی شخصی است که عملیات محاسبات را به انجام می‌رساند. توجه کنید که هر جزء ماشین، یعنی حالت‌ها و علامت‌ها و همچنین هر عملکرد ماشین یعنی چاپ، پاک‌کردن و حرکت دادن نوار متناهی، گسسته و قابل جداسازی بوده و میزان حافظه در دسترس آن یعنی نوار کاملاً نامتناهی است. یکی از مواردی که امکان دارد پیچیدگی خاصی در بر داشته باشد، state یا حالت ماشین است که می‌توان دو برداشت مختلف از آن داشت. بسیاری از افرادی که پس از تورینگ به مباحثه درباره ماشین وی پرداخته‌اند از عبارت حالت برای اشاره به نام یا مشخص‌کردن دستورالعملی که باید اجرا شود (مانند محتویات رجیستر حالت) استفاده کرده‌اند اما تورینگ در سال 1936 یک تفاوت کاملاً آشکار میان رکوردهای پیکربندی یا حالات درونی ماشین با حالت پیشرفت آن در روال محاسبات قائل بود و به همین دلیل، فرمول حالت وی حاوی دستورالعمل جاری به همراه کلیه علامت‌های روی نوار در نظر گرفته شده بود.

بعدها و در سال 1979، مفهوم ماشین تورینگ توسط هاپ کرافت (Hopcroft) و اولمن بر‌اساس پیشرفت‌های حاصل شده، به طور کاملاً مناسب و به‌صورت هفت گانه و بر اساس <M=<Q,Γ,b,Σ,δ,q0,F فرمول‌بندی و منظم شد که در آن متغیرهای مورد استفاده به ترتیب نشان از مجموعه حالات سیستم (Q)، الفبای استفاده شده روی نوار(Γ)، علامت نشانگر فضای خالی(b)، مجموعه علامات ورودی (Σ)، جدول ‌گذار حالت‌ها(δ)، حالت اولیه (q0 ) و حالت‌های نهایی قابل قبول (F ) دارند. هر چیزی که با این مفهوم قابل توصیف باشد، یک ماشین تورینگ به شمار می‌آید. مثالی در این زمینه، ماشین Busy Beaver معروف است که برای رسیدن به بیشینه درگیری عملیاتی در میان ماشین‌های تورینگ موجود در یک کلاس مشخص مطرح شده و مورد استفاده قرار می‌گیرد. توصیف این ماشین بر اساس مدل‌سازی مطرح شده در بالا چنین خواهد بود:

{Q = { A, B, C, HALT
{Γ = { 0, 1
«تهی»=b=o
{Σ = {1
جدول 1= δ
حالت اولیه = q0 = A
مجموعه حالت تک عضوی {F = {HALT

ماشین‌های تورینگ مجازی

در کنار انواع نمونه‌های سخت‌افزاری ساخته شده، پیاده‌سازی‌های رایانه‌ای مختلفی از ماشین تورینگ وجود دارد که با سر زدن و مشاهده روند کاری‌ آن‌ها، می‌توانید به خوبی با نحوه کار ماشین تورینگ آشنا شوید. یکی از این ماشین‌های شبیه‌سازی شده که اتفاقاً ساده‌ترین و معمولی‌ترین آن‌ها نیز به شمار می‌آید در آدرسwww.turing.org.uk/turing/scrapbook/tmjava.html وجود دارد و از طریق یک مرورگر معمولی قابل دسترسی است. در این ماشین، می‌توانید عملیات مربوطه را انتخاب کرده و با زدن Load داده‌های مربوطه را روی نوار نوشته و سپس با زدن Run نتیجه اجرای عملیات روی نوار مذکور را ببینید. (شکل1)

پیاده سازی نرم افزاری ماشین تورینگ به صورت سریع از http://www.turing.org.uk/book/update/tmjavar.html

مثال قبل، نمونه چندان خوبی برای درک شهودی عملکرد ماشین تورینگ نیست چرا که عملیات خود را به یکباره و سریع انجام می‌دهد.
در نقطه مقابل، نمونه پیاده‌سازی شده در آدرس http://ironphoenix.org/tril/tm/ عملکرد بصری مناسبی داشته و با رعایت انجام با فاصله عملیات، درک بهتری از کارکرد ماشین تورینگ با برنامه های مختلف را ارائه می‌کند. (شکل2)

پیاده سازی نرم افزاری ماشین تورینگ به صورت مرحله به مرحله از http://ironphoenix.org/tm/

یک نمونه جالب دیگر از شبیه‌سازی‌های نرم‌افزاری از ماشین‌های تورینگ، شبیه‌سازی مخصوص iOS آن است که از طریق فروشگاه App Store قابل دانلود است. این برنامه، علاوه بر اجرای عملیات ماشین تورینگ به‌صورت بصری، برنامه‌های پیش‌فرض و همچنین قابل ویرایشی را نیز به همراه توضیحات کاملی از عملکرد هر‌کدام در اختیارکاربر می‌گذارد. (شکل3)

شبیه سازی نرم افزاری ماشین تورینگ مخصوص ios قابل دانلود از App store

جدول ‌گذار حالت‌های این ماشین که برای 2 علامت و 3 حالت طراحی شده، در جدول 1 آورده شده است. در این جدول علامت P به معنای چاپ یک روی نوار بوده و L و R به ترتیب به معنای انتقال نوار به چپ و راست است. این جدول را می‌توان به‌صورت دیاگرام انتقال حالت نیز نشان داد. اگرچه جدول‌های بزرگ انتقال حالت بهتر است به‌صورت جدولی باقی بمانند و این گونه قابلیت فهم بالاتری دارند، با این حال نمایش وضعیت ماشین‌های ساده به‌صورت دیاگرامی می‌تواند درک بهتر و ساده‌تری از آن‌ها را ارائه کند. توجه داشته باشید که دیاگرام‌های انتقال حالت، یک تصویر فریز‌‌شده از جدول عملکرد ماشین در زمان است و نباید آن را منحنی عملکرد محاسبات ماشین در طول زمان و مکان دانست. شکل 1 نمایی از دیاگرام انتقال حالت ماشین سه حالته Busy Beaver را نشان می‌دهد. با این حال، هر بار که ماشین Busy Beaver شروع به کار می‌کند، یک منحنی عملکردی را از آغاز تا پایان می‌پیماید اما یک ماشین کپی‌کننده که می‌تواند پارامترهای ورودی متغیر داشته باشد، ممکن است منحنی متفاوتی را طی کند. برای تعیین نحوه عملکرد صحیح یک ماشین در طول زمان به سادگی می‌توان از دیاگرام پیشرفت محاسبات استفاده کرد که نمونه‌ای از آن برای ماشین 3 حالته Busy Beaver در شکل 2 آورده شده است.

جدول گذار حالت های یک ماشین تورینگ

ماشین تورینگ چیست ؟ قسمت 1
ماشین تورینگ چیست ؟ قسمت 2
ماشین تورینگ چیست ؟ قسمت 3

آگوست 23, 2019/0 دیدگاه /توسط hgadmin

ماشین تورینگ چیست ؟ قسمت 1

آموزش های عمومی هوش مصنوعی

ماشین‌تورینگ

ماشین تورینگ (به انگلیسی: Turing machine) یک دستگاه فرضی است که روی نشان‌های روی یک قطعه نوار بر اساس جدول قوانین دست‌کاری انجام می‌دهد. با وجود اینکه مکانیزم ماشین تورینگ مقدماتی است، مفهومش برای پوشش عملکردهای بسیار پیچیده کافی و گسترده‌است. ماشین تورینگ می‌تواند برای شبیه‌سازی هر الگوریتم کامپیوتری و توضیح نحوه عملکرد یک واحد پردازشگر مرکزی به کار آید. حافظه این ماشین ساختاری بسیار ساده دارد. یعنی می‌تواند بصورت یک آرایه یک بعدی از عناصر (سلولها) باشد که هر یک می‌توانند حافظ تنها یک نماد باشند. این آرایه از هر دو طرف باز و نامحدود است (حافظه بینهایت) و اطلاعات آن می‌توانند به هر ترتیبی فراخوانی شوند.

نمایش هنری یک ماشین تورینگ

ماشین‌های تورینگ
ماشین محاسبه تورینگ ماشین تورینگ متناوب ماشین تورینگ کوانتومی ماشین تورینگ غیرقطعی ماشین خواندنی تورینگ ماشین راستگرد خواندنی تورینگ ماشین تورینگ احتمالی ماشین تورینگ چندمسیره ماشین‌های هم‌ارز با ماشین تورینگ

تاریخچه

زمینه‌های تاریخی:ماشین محاسباتی

معرفی ماشین تورینگ توسط دانشمند انگلیسی آلن تورینگ در سال ۱۹۳۶ میلادی، گام دیگری را در مسیر ایجاد و پیدایش ماشین‌های محاسباتی حالات متناهی به نمایش می‌گذارد. رابین گندی یکی از دانشجویان آلن تورینگ و دوست صمیمی تمام عمرش، ریشه‌های نظریه ماشین محاسباتی بابیج(۱۸۳۴) را کاوش کرد و در حقیقت نظریه بابیج را دوباره ارائه کرد:

آنالیز گندی در مورد ماشین تحلیلی بابیج پنج عملیات زیر را توضیح می‌دهد:

۱-عملگرهای ریاضی + و – و *

۲-هر ترتیبی از عملگرها قابل قبول است

۳-تکرار عملگر

۴-تکرار شرطی

۵-انتقال شرطی

تعریف منطقی (انتزاع ذهنی مفاهیم کلی)

ماشین تورینگ عبارت است از یک پنج-تاپل (پنج‌تایی) به‌صورت $M=(Q,\Sigma ,\Gamma ,\delta ,q_{0})\!$ ، که در اینجا:

$M\!$ برای نمایش مفهوم ماشین انتخاب شده است.
$Q\!$ مجموعه‌ای است متناهی، از حالات داخلی.
$\Gamma \!$ مجموعه‌ای متناهی موسوم به الفبای نوار و حاوی نمادی مخصوص $B\!$ برای نمایش یک فاصلهٔ خالی روی نوار ماشین است.
$\Sigma \!$ زیرمجموعه‌ای است از $\Gamma -\{B\}\!$ و موسوم به الفبای ورودی. یعنی الفبای ورودی زیر مجموعه‌ای از الفبای نوار است که شامل خالی نیست. نوارهای خالی نمی‌توانند بعنوان ورودی استفاده شوند.
$\delta \!$ عبارت است از یک تابع جزئی، موسوم به تابع انتقال از دامنهٔ $Q\times \Gamma \!$ به برد $Q\times \Gamma \times \{L,R\}\!$ .
$q_{0}\!$ حالت شروع نام دارد، یعنی، حالتی از ماشین است که محاسبه را درآن آغاز می‌کنیم.

بطور کلی $\delta \!$ یک تابع جزئی روی $Q\!\times \Gamma \!$ است و تفسیرش عملکرد ماشین تورینگ را بیان می‌کند.

تعریف وصفی (عملی دنیای خارج از ذهن)

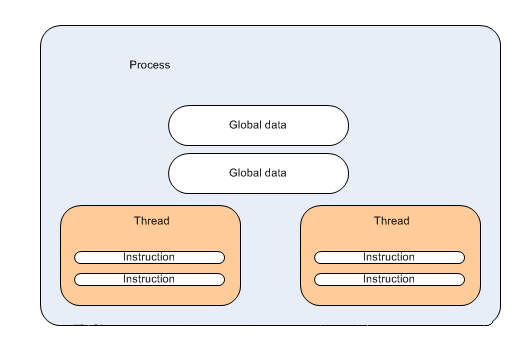
ماشین تورینگ به صورت ریاضی، ماشینی است که روی یک نوار عمل می‌کند. روی این نوار، نمادهایی است که ماشین هم می‌تواند بخواند و هم می‌تواند بنویسد و همزمان از آنها استفاده می‌کند. این عمل به طور کامل با یک سری دستورالعمل ساده و محدود تعریف شده است. ماشین تورینگ از موارد زیر تشکیل شده است:

۱. یک نوار، به سلولهایی تقسیم‌بندی شده است و هر سلول شامل نمادهایی است. الفبا شامل نماد تهی خاصی و یک یا تعداد دیگری نماد است. فرض می‌شود که این نوار خودسرانه به چپ و راست رسانده شود. ماشین تورینگ از نوارهایی تأمین می‌شود که برای محاسبه لازم است.

۲. یک کلاهک وجود دارد که قادر به خواندن و نوشتن نمادهایی است که روی نوار قرار گرفته‌اند و بطور همزمان نوار را به سمت چپ و راست یکی از (و تنها یک) سلولها حرکت می‌دهد. در بضی مدلها، کلاهک حرکت می‌کند و نوار ثابت می‌ماند.

۳. یک دستگاه ثبت حالت وجود دارد که حالت‌های ماشین تورینگ را ذخیره می‌کند (یکی از تعداد زیادی حالت متناهی). یک حالت شروع وجود دارد که همراه با مقدار دهی اولیه است. این حالت‌ها، حالت ذهن شخصی را که محاسبات را انجام می‌دهد، جایگزین می‌کنند.

۴. یک جدول محدود (که گاهی جدول عمل یا تابع انتقال نامیده می‌شود)، از دستورالعمل‌ها وجود دارد که در حال حاضر، حالت (q_i) و نماد (a_j) به ماشین داده می‌شود (برای مدل‌های ۵تایی و گاهی ۴تایی) که روی نوار خوانده می‌شود و می‌گوید که ماشین، این موارد را به تزتیب زیر برای مدلهای ۵تایی انجام دهد:

یا پاک کردن یا نوشتن یک نماد (بصورت جایگزین کردن a_i با a_j۱)
حرکت کردن کلاهک نوار (که توسط d_k مشخص می‌شود و می‌تواند مقادیر L برای حرکت به چپ و R برای حرکت به سمت راست به خود بگیرد. همچنین مقدار N نشان دهنده ساکن بودن نوار است).
فرض کنید یک حالت مشابه یا یک حالت جدید مشخص شده است (رفتن به وضعیت q_i۱)

در مدل‌های ۴تایی پاک کردن یا نوشتن یک نماد (a_j۱) و حرکت کلاهک نوار به سمت چپ یا راست (d_k) بصورت دستورالعمل‌های جداگانه مشخص شده‌اند. بطور خاص، جدول به ماشین می‌گوید که چیزی را پاک کند یا یک نماد را بنویسد (ia) یا کلاهک نوار به سمت چپ و راست حرکت کند (ib). فرض کنید که حالتهای مشابه یا حالتهای جدیدی مشخص شده‌اند. اما عملیات‌های (ia) و (ib) دستورالعمل‌های یکسانی ندارند. در برخی از مدلها، اگر در جدول، ورودی از نمادها و حالتها نداشته باشیم، ماشین متوقف خواهد شد. سایر مدلها، نیاز به همه ورودی‌ها دارند تا پر شوند. توجه داشته باشید که هر بخش از ماشین- حالتها و نمادها، مجموعه‌ها، اقدامات، چاپ کردن، پاک کردن و حرکت نوار- محدود، گسسته و تشخیص پذیر است. این، پتانسیل نامحدود نوارهاست که خود مقدار نامحدودی از یک فضای ذخیره‌سازی است.

مقایسه با ماشین‌های واقعی

اغلب گفته می‌شود که ماشین تورینگ، بر خلاف ماشین‌های اتومات، به اندازه ماشین‌های واقعی قدرتمند هستند و قادر به انجام هر عملیاتی که ماشین واقعی می‌تواند بکند هستند. چیزی که در این مطلب جا ماند این است که یک ماشین واقعی تنها می‌تواند در بسیاری از تنظیمات متناهی باشد؛ در واقع ماشین واقعی چیزی نیست جز یک ماشین اتوماتیک محدود خطی. از طرف دیگر ماشین تورینگ با ماشین‌هایی که دارای ظرفیت حافظه‌های نامحدود محاسباتی هستند، معادل است. از نظر تاریخی رایانه‌هایی که محاسبات را در حافظه داخلی شان انجام می‌دادند، بعدها توسعه داده شده‌اند.

چرا ماشین‌های تورینگ مدل‌های مناسبی برای رایانه‌های واقعی هستند؟

۱. هرچیزی که ماشین واقعی می‌تواند محاسبه کند، ماشین تورینگ هم می‌تواند. برای مثال ماشین تورینگ، می‌تواند هرچیز طبق روالی که در زبان‌های برنامه‌نویسی پیدا می‌شود شبیه‌سازی کند. همچنین می‌تواند فرایندهای بازگشتی و هریک از پارامترهای مکانیسم شناخته شده را شبیه‌سازی کند.

۲. تفاوت، تنها در قابلیت ماشین تورینگ برای دخالت در مقدار محدودی اطلاعات نهفته است؛ بنابراین، ماشین تورینگ می‌تواند در مدت زمان محدودی، در اطلاعات دخالت داشته باشد.

۳. ماشین واقعی همانند ماشین‌های تورینگ می‌توانند حافظه مورد نیازش را به کمک دیسک‌های بیشتر، بزرگ کند. اما حقیقت این است که هم ماشین تورینگ و هم ماشین واقعی، برای محاسبات نیازی به فضا در حافظه‌شان ندارند.

۴. شرح برنامه‌های ماشین واقعی که از مدل ساده‌تر انتزاعی استفاده می‌کنند، پیچیده‌تر از شرح برنامه‌های ماشین تورینگ است.

۵. ماشین تورینگ الگوریتم‌های مستقل را که چقدر از حافظه استفاده می‌کنند، توصیف می‌کند. در دارایی حافظه همهٔ ماشین‌ها، محدودیتی وجود دارد؛ ولی این محدودیت می‌تواند خود سرانه در طول زمان افزایش یابد.

ماشین تورینگ به ما اجازه می‌دهد دربارهٔ الگوریتم‌هایی که برای همیشه نگه داشته می‌شوند، توصیفاتی ارائه دهیم؛ بدون در نظر گرفتن پیش رفت در معماری محاسبات با ماشین معمولی.

۶. ماشین تورینگ جملات الگوریتم را ساده می‌کند. الگوریتم‌های در حال اجرا در ماشین آلات انتزاعی معادل تورینگ، معمولاً نسبت به همتایان خود که در ماشین‌های واقعی در حال اجرا هستند عمومی ترند. زیرا آنها دارای دقت دلخواه در انواع اطلاعات قابل دسترس هستند و هیچوقت با شرایط غیرمنتظره روبرو نمی‌شوند. یکی از نقطه ضعف‌های ماشین تورینگ این است که برنامه‌های واقعی که نوشته می‌شوند ورودی‌های نامحدودی را در طول زمان دریافت می‌کنند؛ در نتیجه هرگز متوقف نمی‌شوند.

محدودیت‌های ماشین تورینگ

نظریه پیچیدگی محاسباتی

یکی از محدودیت‌هاو معایب ماشین‌های تورینگ این است که آنها توانایی چیدمان خوب را ندارند. برای مثال کامپیوترهای برنامه‌ای با ذخیره مدرن، نمونه‌هایی از یک مدل خاص ماشین انتزاعی که به نام ماشین برنامه دسترسی رندم یا مدل ماشین RASP می‌باشند.

همزمانی

یکی دیگر از محدودیت‌های ماشین تورینگ این است که همزمانی را خوب ارئه نمی‌دهد. برای مثال برای اندازه عدد صحیحی که می‌تواند توسط «متوقف کننده غیر قطعی دایمی» محاسبه شود، محدودیت وجود دارد. ماشین تورینگ روی یک نوار خالی شروع می‌کند. در مقابل، ماشین‌های «همیشه متوقف» همزمان هستند که بدون ورودی می‌توانند عدد صحیح نامتناهی را محاسبه کنند.

منبع

ایده ماشین تورینگ چگونه مطرح شد و چه چیزی را دنبال می‌کرد؟

بخش اول

ماشین تورینگ! مفهومی که به اندازه فرد مطرح کننده خود از اهمیت ویژه‌ای برخوردار است و نقش مهمی در رسیدن علوم کامپیوتر و همچنین فناوری محاسبات به مقطع کنونی دارد. اگرچه به سادگی می‌توان بدون داشتن اطلاعاتی حتی جزئی در رابطه با ماشین تورینگ، به خوبی از نحوه کارکرد كامپيوترها و سازوكار محاسبات در ماشین‌ها مطلع شد اما در این حالت، قطعاً کلید اصلی مسئله در نظر گرفته نشده است. درک ماشین تورینگ، درک روح محاسبات ماشینی و شناخت تولد و تکامل ماشین‌های محاسبه‌گر است. اما به راستی، تورینگ چگونه و با چه هدفی چنین ایده‌ای را مطرح کرد؟

سرآغاز

تاریخچه محاسبات دیجیتال به دو بخش عهد عتیق و عهد جدید قابل تقسیم است. پیشوایان عهد قدیم به سرپرستی لایبنیتز (Gottfreid Wilhelm Leibniz) در سال 1670 میلادی منطق مورد نیاز ماشین‌های محاسباتی دیجیتال را فراهم کرده و پیشروان عهد جدید به سرپرستی فون نویمان (John von Neumann) در سال 1940 خود این ماشین‌ها را ساختند. آلن تورینگ، که در سال 1912 متولد شده است، جایی در میان این دو عصر مهم قرار گرفته و شاید بتوان وی را به نوعی پیوند دهنده این دو عهد مهم به شمار آورد. وی در سال 1936، درست در زمانی که به تازگی از کالج کینگ در دانشگاه کمبریج فارغ‌التحصیل شده و به دانشگاه پرینستون در نیوجرسی امریکا رفته بود، با نگارش و انتشار مقاله‌ای با عنوان «درباره اعداد رایانش‌پذیر، ‌با کاربردی بر مسئله تصمیم‌گیری» (On Computable Numbers, with an application to the Entscheidungs problem )، راهنمای پیاده‌سازی ماشین‌های با منطق ریاضی شد.

در این مقاله، تورینگ قصد داشت تا مسئله Entscheidungs problem ریاضی‌دان آلمانی، دیوید هیلبرت (David Hilbert) را که در سال 1928 طرح کرده بود، حل کند. موضوع نهایی مسئله فوق، تصمیم‌گیری درباره این بود که آیا یک روال مکانیکی می‌تواند صحت یک عبارت منطقی را در تعداد محدودی حرکت تعیین کند یا خیر؟ تورینگ در این مقاله، ایده و تصور رایج در دهه 1930 از یک کامپیوتر (یک شخص مجهز به یک مداد، کاغذ و دستورالعمل‌های مشخص) را در نظر گرفته و با حذف تمام رگه‌های هوشمندی (Intelligence) از آن به غیر از امکان پیروی از دستورالعمل‌ها و امکان خواندن و نوشتن علامت‌هایی از یک الفبای خاص روی یک رول کاغذ با طول بی نهایت، ماشینی را معرفی کرد که بعدها به ماشین تورینگ معروف شد و سرآغاز طلوع ماشین‌های محاسباتی دیجیتال امروزی شد.

ماشین تورینگ، یک جعبه سیاه ریاضیاتی بود که از یک سری دستورالعمل از پیش تعیین شده پیروی می‌کرد. این دستورالعمل‌ها با استفاده از علامت‌هايي مشخص که روی کاغذ یا نوع خاصی از حافظه نوشته می‌شد به ماشین تحویل داده می‌شد. این ماشین می‌توانست در هر لحظه، یک علامت را از روی یک خانه خوانده، نوشته یا پاک کند و خانه مذکور را که یک واحد کوچک موجود روی رول کاغذ است به سمت چپ یا راست هدایت کند. علامت‌های پیچیده می‌توانند به‌صورت دنباله‌ای از علامت‌های ساده‌تر پیاده‌سازی شوند و در این حالت، پیچیدگی احتمالی، تشخیص تفاوت بین دو علامت مختلف و وجود یا نبود فاصله‌های خالی روی نوار است. «بیت»های اطلاعاتی در این ماشین می‌توانند دو فرم مختلف داشته باشند: الگوهایی در فضا که در طول زمان ارسال می‌شوند و حافظه مدت‌دار خوانده می‌شوند یا الگوهایی در زمان که در فضا ارسال شده و کد نامیده می‌شوند. در ماشین تورینگ، زمان به‌صورت رشته‌ای از اتفاقات یکسان نیست، بلکه به صورت دنباله‌ای از تغییر حالات در ماشین مذکور قابل تصور خواهد بود.

ایده ماشین‌های بدون قطعیتِ پیشگو، به اساس کار هوش نزدیک‌تر بود؛ شهود و بینش، پر‌کننده فاصله میان عبارات منطقی است.

در ادامه مقاله، تورینگ امکان وجود ماشین منفردی را مطرح کرد که می‌تواند هر توالی محاسباتی‌ را محاسبه کند. «چنین ماشین محاسباتی جامعی می‌تواند رفتار هر ماشین دیگری را با استفاده از شرح کار کد شده آن تقلید کند.» بنابراین، با ذکر این عبارت، تورینگ ایده «نرم‌افزار» را در حدود 76 سال قبل پیشگویی کرده بود. در پایان، تورینگ مسئله پیچیده هیلبرت را به روشی جالب پاسخ داده است. او عبارتی را یافته بود که در تعداد گام‌های محاسباتی محدود، توسط هیچ ماشینی قابل محاسبه نبود: آیا شرح کار کد شده یک ماشین که توسط ماشین محاسباتی جامع تورینگ اجرا می‌شود، در نهایت به پایان می‌رسد یا برای همیشه اجرا می‌شود؟

بر همین اساس، وی پاسخ مسئلهEntscheidungs problem را منفی دانسته و از این طریق، پايه‌گذار طراحی ماشین‌های محاسباتی دیجیتال شد. در سال 1949، فون‌نویمان در یک سخنرانی با اشاره به این مفهوم مطرح شده توسط تورینگ عنوان کرد: «شما می‌توانید چیزی بسازید که کاری را که می‌شود انجام داد، انجام دهد. اما نمی‌توانید نمونه‌ای بسازید که به شما بگوید که آیا آن کار انجام‌پذیر است یا خیر؟»
تورینگ با درک محدودیت‌های ماشین‌های با قطعیت مشخص، شروع به جست‌وجو در زمینه محاسبات غیر‌قطعی با ماشین‌های پیشگو کرد. از نظر او، این نوع ماشین‌ها، همان روال گام به گام را مورد استفاده قرار می‌دهند اما با استفاده از نوعی پیشگویی، گاهی جهش‌هایی غیرقابل پیش‌بینی نیز انجام می‌دهند.

رمزگشایی

پس از پایان تحصیلات در دوره دکترا، تورینگ در سال 1938 به انگلیس بازگشت و گسترش جنگ جهانی دوم منجر به بروز نیاز هرچه بیشتر به ایده‌های وی شد. به همین دلیل، وی در مدرسه رمز و کدهای محرمانه دولت به خدمت گرفته شد. در آنجا، تورینگ و همکارانش به همراه استادش، ماکسول نیومن (Maxwell Newman) ارتباطات دشمن را، از جمله پیام‌های کدگذاری شده توسط ماشین آلمانی انيگما، رمزگشایی کردند. انیگما، ماشینی شبیه به ماشین تورینگ بود که امکان کد‌گذاری متن ورودی خود را با مکانیزمی مکانیکی فراهم می‌کرد. آن‌ها کار کدگشایی رمزهای انیگما را با مجموعه‌ای از دستگاه‌های الکترومکانیکی که بمب (bombe) نامیده می‌شدند، شروع کردند که هر کدام می‌توانست در هر لحظه 36 حالت احتمالی پیکربندی انیگما را شبیه‌سازی کند.

از این طریق، آن‌ها توانستند با همکاری افرادی دیگر، کامپیوتری بسیار پیچیده و دیجیتال با نام Clossus بسازند که از یک حافظه داخلی ساخته شده با 1500 لامپ خلاء بهره می‌برد که وضعیت حافظه برنامه‌پذیری را برای جست‌وجوی کدها فراهم می‌کرد. این مدل بعدها با نسل دوم خود با 2400 لامپ خلاء جایگزین شد که علاوه بر تأثیر اساسی بر نتیجه جنگ، تحولی شگرف در تکامل رایانه‌های دیجیتال به شمار می‌آمد. اسرار مربوط به ساخت این ماشین برای حدود 30 سال از طرف سازمان‌های اطلاعاتی انگلیس به‌صورت محرمانه نگه‌داری می‌شد.

پس از پایان جنگ، نیاز به کامپیوترهای پیشرفته‌تر، از کاربردهای رمزگشایی به سمت طراحی بمب‌های اتمی پیش رفت. در سال 1946 ایالات‌متحده با داشتن کامپیوتر زمان جنگ خود، یعنی ENIAC (سرنام Electronic Numerical Integrator and Computer)، کار روی طراحی سلاح‌های اتمی را در پیش گرفت. در انستیتو مطالعات پیشرفته پرینستون و با حمایت مالی ارتش ایالات‌متحده، دفتر تحقیقات نیروی دریایی و همچنین کمیسیون انرژی اتمی امریکا، فون‌نویمان موظف شد تا نمونه الکترونیکی ماشین جامع تورینگ را بسازد. در آن زمان، هدف او ساخت ماشین تورینگی بود که حافظه آن با سرعت نور قابل دسترسی بوده و به پردازش در زمینه‌های مختلف می‌پرداخت. اما هدف دولت ایالات متحده امریکا از سرمایه‌گذاری روی چنین ماشینی تعیین امکان ساخت بمب هیدروژنی بود و به همین دلیل، فون نویمان قول داد که ماشین مذکور که از 5 کیلوبایت فضای ذخیره‌سازی بهره می‌برد، امکان اجرای کدهای داینامیک مذکور را داشته باشد.

بعدها، طراحی کامپیوتر مذکور در اختیار همگان گذارده شد و آي‌بي‌ام آن را تجاری کرد. در نخستین جلسه هماهنگی برای اجرای پروژه مذکور در سال 1945، فون نویمان اعلام کرد که قصد دارد پیاده‌سازی دستورات را نیز همانند اعداد در حافظه انجام دهد و این ترکیب داده‌ها و دستورالعمل‌ها کاملاً بر‌اساس مدل تورینگ بود.