بایگانی‌های کنترل تردد

بایگانی برچسب برای: کنترل تردد

تعریف رگرسیون خطی (Linear Regression) قسمت 5

برآورد پارامترهای رگرسیون خطی ساده

به منظور برآورد پارامترهای رگرسیون خطی ساده، کافی است تابع مجموع مربعات خطا را کمینه کرد. برای این کار مراحل زیر باید طی شوند:

محاسبه مجموع توان دوم خطا

$\sum (y_{i} - ({ˆ β}_{0} + {ˆ β}_{1} x_{i}))^{2}$

مشتق مجموع مربعات خطا برحسب پارامتر ${ˆ β}_{0}$

$\sum (- y_{i} + {ˆ β}_{0} + {ˆ β}_{1} x_{i})$

برابر قرار دادن مشتق با صفر به منظور پیدا کردن نقاط کمینه

$\sum (- y_{i} + {ˆ β}_{0} + {ˆ β}_{1} x_{i}) = 0$

پیدا کردن ریشه برای معادله حاصل برحسب ${ˆ β}_{0}$

${ˆ β}_{0} = ¯ y - {ˆ β}_{1} ¯ x$

مشتق مجموع مربعات خطا بر حسب پارامتر ${ˆ β}_{1}$

$\sum (- 2 x_{i} y_{i} + 2 {ˆ β}_{0} x_{i} + 2 {ˆ β}_{1} x_{i}^{2})$

جایگذاری ${ˆ β}_{0}$ و پیدا کردن ریشه برای معادله حاصل برحسب ${ˆ β}_{1}$

$- \sum (x_{i} y_{i} + (¯ y - {ˆ β}_{1} ¯ x) \sum x_{i} + {ˆ β}_{1} \sum x_{i}^{2}) = 0$

$_{1} = \frac{\sum (x_{i} - ¯ x) (y_{i} - ¯ y)}{\sum (x_{i} - ¯ x)^{2}}$

به این ترتیب برآورد پارامترهای مدل خطی به صورت زیر خواهند بود.

$_{1} = \frac{\sum (x_{i} - ¯ x) (y_{i} - ¯ y)}{\sum (x_{i} - ¯ x)^{2}}$

$_{0} = ¯ y -_{1} ¯ x$

که در آن $¯ x$ و $¯ y$ میانگین $x$ و $y$ هستند.

برای راحتی محاسبات، می‌توان برآورد $β_{1}$ را به فرم دیگری نیز نوشت:

$_{1} = \frac{n (¯ ¯¯¯¯ ¯ x y - ¯ x ¯ y))}{(n - 1) σ_{x}^{2}}$

که منظور از $¯ ¯¯¯¯ ¯ x y$ میانگین حاصلضرب x و y بوده و $σ_{x}^{2}$ نیز بیانگر واریانس مقدارهای x است.

اگر $ˆ y$ مقدار برآورد برای متغیر وابسته باشد، می‌توانیم آن را میانگین مشاهدات برای متغیر وابسته به ازای مقدار ثابت متغیر مستقل در نظر گرفت. پس با فرض اینکه میانگین جمله خطا نیز صفر است، خواهیم داشت:

$ˆ y = E (Y | X = x) =_{0} +_{1} x$

که در آن $E (Y | X = x)$ نشان‌دهنده امید ریاضی (متوسط) شرطی است و همچنین $_{0}$ و ${ˆ β}_{1}$ برآوردهای مربوط به هر یک از پارامترها هستند.

نکته: به راحتی دیده می‌شود که میانگین مربوط به متغیر مستقل و وابسته روی خط رگرسیون قرار دارند. یعنی این نقطه در معادله خط رگرسیون صدق می‌کند. زیرا با توجه به محاسبه $β_{0}$ داریم:

$_{0} = ¯ y -_{1} ¯ x \to ¯ ¯¯ ¯ Y = {ˆ β}_{0} + {ˆ β}_{1} ¯ ¯¯¯ ¯ X$

مثال

اطلاعات مربوط به ۵۰ خانه شامل قیمت (به میلیون ریال) و متراژ (متر مربع) در شهر تهران جمع‌آوری شده است. این اطلاعات را می‌توانید با قالب اکسل از اینجا دریافت کنید.

با توجه به ضریب همبستگی بین این دو متغیر که برابر با 0.9891 است،‌ مشخص است که رابطه خطی شدیدی بینشان برقرار است. اگر فرض کنیم قیمت خانه متغیری وابسته به متراژ است، محاسبات اولیه برای برآورد پارامترهای مدل رگرسیونی در جدول زیر قرار گرفته.

$¯ ¯¯¯ ¯ X$	$¯ ¯¯ ¯ Y$	$¯ ¯¯¯¯¯¯¯ ¯ X Y$	$σ_{X}^{2}$
84.9	451.136	40350.6	411.724

بر این اساس برآورد پارامترهای مدل خطی به صورت ${ˆ β}_{0} = 19.965$ و ${ˆ β}_{1} = 5.078$ خواهد بود. در نتیجه می‌توان معادله مربوط برآورد مقدار متغیر وابسته را به صورت زیر نوشت:

$_{i} = 19.965 + 5.078 x_{i}$

پس اگر لازم باشد که ارزش خانه‌ای با متراژ 61 متر محاسبه شود، کافی است در معادله بالا برای $x_{i}$ ‌ مقدار 61 را جایگزین کرده،‌ مقدار ${ˆ y}_{i}$ را بدست آوریم که برابر با 329.758 میلیون ریال است. در تصویر زیر نمودار مربوط به داده‌ها و خط رگرسیون دیده می‌شود.

$_{i} = 19.965 + 5.078 (61) = 329.758$

تعریف رگرسیون خطی (Linear Regression) قسمت 1
تعریف رگرسیون خطی (Linear Regression) قسمت 2
تعریف رگرسیون خطی (Linear Regression) قسمت 3
تعریف رگرسیون خطی (Linear Regression) قسمت 4
تعریف رگرسیون خطی (Linear Regression) قسمت 5
تعریف رگرسیون خطی (Linear Regression) قسمت 6
تعریف رگرسیون خطی (Linear Regression) قسمت 7

آگوست 25, 2019/0 دیدگاه /توسط hgadmin

تعریف رگرسیون خطی (Linear Regression) قسمت 4

آموزش عمومی پردازش تصویر و بینایی ماشین

مفهوم رگرسیون

در آمار، رگرسیون خطی یک روریکرد مدل خطی بین متغیر «پاسخ» (Response) با یک یا چند متغیر «توصیفی» (Explanatory) است. اغلب برای کشف مدل رابطه‌ی خطی بین متغیرها از رگرسیون (Regression) استفاده می‌شود. در این حالت فرض بر این است که یک یا چند متغیر توصیفی که مقدار آن‌ها مستقل از بقیه متغیرها یا تحت کنترل محقق است، می‌تواند در پیش‌بینی متغیر پاسخ که مقدارش وابسته به متغیرهای توصیفی و تحت کنترل محقق نیست، موثر باشد. هدف از انجام تحلیل رگرسیون شناسایی مدل خطی این رابطه‌ است.

در ادامه از متغیر وابسته به جای متغیر پاسخ و متغیر مستقل به جای متغیر توصیفی استفاده می‌کنیم.

از آنجایی که ممکن است علاوه بر متغیرهای مستقل، عوامل زیاد و ناشناخته‌ دیگری نیز در تعیین مقدار متغیر وابسته نقش داشته باشند، مدل رگرسیونی را با مناسب‌ترین تعداد متغیر مستقل در نظر گرفته و میزان خطا را به عنوان نماینده عوامل تصادفی دیگری که قابل شناسایی نبودند در نظر می‌گیریم که انتظار است کمتر در تغییرات متغیر وابسته نقش داشته باشند.

تاریخچه رگرسیون

واژه رگرسیون برای اولین بار در مقاله‌ معروف فرانسیس گالتون دیده شد که در مورد قد فرزندان و والدینشان بود. این واژه به معنی بازگشت است. او در مقاله خود در سال 1۸۷۷ اشاره می‌کند که قد فرزندان قد بلند به میانگین قد جامعه میل می‌کند. او این رابطه را «بازگشت» (Regress) نامید.

هر چند واژه رگرسیون در شاخه علوم زیستی معرفی شد ولی آنچه امروزه به نام رگرسیون می‌شناسیم،‌ روشی است که توسط «گاوس» (Gauss) در سال 1۸۰۹ معرفی شد تا به کمک آن پارامترهای مجهول رابطه بین مدار سیاره‌های منظومه شمسی را برآورد کند.

بعدها روش گاوس توسط پیرسون (Pearson) توسعه یافت و با مفاهیم آماری آمیخته شد. همچنین پیرسون توزیع توام متغیر وابسته و مستقل را توزیع گاوسی در نظر گرفت. بعدها «فیشر» (R. A. Fisher) توزیع متغیر وابسته به شرط متغیر مستقل را توزیع گاوسی محسوب کرد.

مدل رگرسیون خطی ساده

اگر برای شناسایی و پیش‌بینی متغیر وابسته فقط از یک متغیر مستقل استفاده شود، مدل را «رگرسیون خطی ساده» (Simple Linear Regression) می‌گویند. فرم مدل رگرسیون خطی ساده به صورت زیر است:

$Y = β_{0} + β_{1} X + ϵ$

همانطور که دیده می‌شود این رابطه، معادله یک خط است که جمله خطا یا همان $ϵ$ ‌ به آن اضافه شده. پارامترهای این مدل خطی عرض از مبدا ( $β_{0}$ ) و شیب خط ( $β_{1}$ ) است. شیب خط در حالت رگرسیون خطی ساده، نشان می‌دهد که میزان حساسیت متغیر وابسته به متغیر مستقل چقدر است. به این معنی که با افزایش یک واحد به مقدار متغیر مستقل چه میزان متغیر وابسته تغییر خواهد کرد. عرض از مبدا نیز بیانگر مقداری از متغیر وابسته است که به ازاء مقدار متغیر مستقل برابر با صفر محاسبه می‌شود. به شکل دیگر می‌توان مقدار ثابت یا عرض از مبدا را مقدار متوسط متغیر وابسته به ازاء حذف متغیر مستقل در نظر گرفت.

برای مثال فرض کنید کارخانه‌ای می‌خواهد میزان هزینه‌هایش را براساس ساعت کار برآورد کند. شیب خط حاصل از برآورد نشان می‌دهد به ازای یک ساعت افزایش ساعت کاری چه میزان بر هزینه‌هایش افزوده خواهد شد. از طرفی عرض از مبدا خط رگرسیون نیز هزینه ثابت کارخانه حتی زمانی که ساعت کاری نیست نشان می‌دهد. این هزینه را می‌توان هزینه‌های ثابت مانند دستمزد نگهبانان و هزینه روشنایی فضای کارخانه فرض کرد.

گاهی مدل رگرسیونی را بدون عرض از مبدا در نظر می‌گیرند و $β_{0} = 0$ محسوب می‌کنند. این کار به این معنی است که با صفر شدن مقدار متغیر مستقل، مقدار متغیر وابسته نیز باید صفر در نظر گرفته شود. زمانی که محقق مطمئن باشد که که خط رگرسیون باید از مبدا مختصات عبور کند، این گونه مدل در نظر گرفته می‌شود. فرم مدل رگرسیونی در این حالت به صورت زیر است:

$Y = β_{1} X + ϵ$

از آنجایی که پیش‌بینی رابطه بین متغیر وابسته و مستقل به شکل دقیق نیست، جمله خطا را یک «متغیر تصادفی» (Random Variable) با میانگین صفر در نظر می‌گیرند تا این رابطه دارای اریبی نباشد.

باید توجه داشت که منظور از رابطه خطی در مدل رگرسیون، وجود رابطه خطی بین ضرایب است نه بین متغیرهای مستقل. برای مثال این مدل $y = β_{0} + β_{1} x^{2} + ϵ$ را نیز می‌توان مدل خطی در نظر گرفت در حالیکه مدل $y = β_{0} x^{β_{1}} + ϵ$ دیگر خطی نیست و به مدل نمایی شهرت دارد.

همچنین در فرضیات این مدل، خطا یک جمله تصادفی است و تغییرات آن مستقل از متغیر X‌ است. به این ترتیب مقدار خطا وابسته به مقدار متغیر مستقل نیست.

در رگرسیون خطی سعی می‌شود، به کمک معادله خطی که توسط روش رگرسیون معرفی می‌شود، برآورد مقدار متغیر وابسته به ازای مقدارهای مختلف متغیر مستقل توسط خط رگرسیون بدست آید. به منظور برآورد پارامترهای مناسب برای مدل، کوشش می‌شود براساس داده‌های موجود، مدلی انتخاب می‌شود که کمترین خطا را داشته باشد.

روش‌های مختلفی برای تعریف خطا و حداقل کردن آن وجود دارد. معیاری که در مدل رگرسیون خطی ساده به کار می‌رود، کمینه کردن مجموع مربعات خطا است. از آنجایی که میانگین مقدارهای خطا صفر در نظر گرفته شده است، می‌دانیم زمانی مجموع مربعات خطا، حداقل ممکن را خواهد داشت که توزیع داده‌ها نرمال باشند. در نتیجه، نرمال بودن داده‌های متغییر وابسته یا باقی‌مانده‌ها یکی از فرضیات مهم برای مدل رگرسیونی خطی ساده است.

شکل زیر به منظور توضیح نرمال بودن مقدار خطا ترسیم شده است. در هر مقدار از متغیر مستقل ممکن است بیش از یک مقدار برای متغیر وابسته مشاهده شود. مقدار پیش‌بینی شده برای هر یک از این مقدارها ثابت است که توسط معادله خط رگرسیون برآورد می‌شود.

برای مثال تعدادی مقدار برای متغیر وابسته براساس مقدار x=65 وجود دارد که شکل توزیع فراوانی آن‌ها به صورت نرمال با میانگین $β_{0} + β_{1} \times 65$ است. همچنین برای نقطه ۹۰ نیز مقدار پیش‌بینی یا برآورد برای متغیر وابسته به صورت $β_{0} + β_{1} \times 90$ خواهد بود. در هر دو حالت واریانس خطا یا واریانس مقدارهای پیش‌بینی‌شده (پهنای منحنی زنگی شکل) ثابت است.

در تصویر زیر چهار نقطه از مشاهدات (x,y) به همراه خط رگرسیون دیده می‌شوند که در آن خط رگرسیون با رنگ آبی، نقطه‌های مربوط به مشاهدات با رنگ قرمز و فاصله هر نقطه از خط رگرسیون (خطای برآورد) با رنگ سبز نشان داده شده است.

Linear_least_squares — نمودار نقطه‌ای متغیر مستقل و وابسته،‌ میزان خطا و خط رگرسیون

برای برآورد کردن پارامترهای مدل رگرسیونی باید معادله خطی یافت شود که از بین همه خطوط دیگر دارای کمترین مجموع توان دوم خطا باشد. یعنی $\sum ϵ^{2}$ برای آن از بقیه خطوط کمتر باشد.

points_for_linear_regression — خطوط مناسب برای بیان رابطه بین متغیر مستقل و وابسته

به نظر شما در تصویر بالا،‌ کدام خط دارای مجموع مربعات خطای کمتری است؟ امکان تشخیص بهترین خط بدون استفاده از ابزارهای محاسباتی امکان‌پذیر نیست.

آگوست 25, 2019/0 دیدگاه /توسط hgadmin

تعریف رگرسیون خطی (Linear Regression) قسمت 3

آموزش عمومی پردازش تصویر و بینایی ماشین

تنظیم مدل (Regularization)

پیچیدگی مدلهای پارامتری با تعداد پارامترهای مدل و مقادیر آن‌ها سنجیده می‌شود. هرچه این پیچیدگی بیشتر باشد خطر بیش‌برازش (Overfitting) برای مدل بیشتر است پدیده بیش‌برازش زمانی رخ می‌دهد که مدل بجای یادگیری الگوهای داده، داده را را حفظ می‌کند و در عمل یادگیری به خوبی انجام نمی‌شود. برای جلوگیری از بیش‌برازش در مدلهای خطی مانند رگرسیون خطی یارگرسیون لجستیک جریمه‌ای به تابع هزینه اضافه می‌شود تا از افزایش زیاد پارامترها جلوگیری شود. به این کار تنظیم مدل یا Regularization گفته می‌شود. دو راه متداول تنظیم مدلهای خطی روشهای $L_{1}$ و $L_{2}$ هستند. در روش $L_{1}$ ضریبی از نُرمِ $L_{1}$ به تابع هزینه اضافه می‌شود و در روش $L_{2}$ ضریبی از نُرمِ $L_{2}$ که همان نُرمِ اقلیدسی است به تابع هزینه اضافه می‌شود.

در تنظیم مدل به روش $L_{1}$ تابع هزینه را به این شکل تغییر می‌دهیم:

$L_{r}(D,{\vec {\beta }})=L(D,{\vec {\beta }})+\lambda ||{\vec {\beta }}||_{1}=\sum _{i=1}^{n}({\vec {\beta }}\,.\,{\vec {x_{i}}}-y_{i})^{2}+\lambda \sum _{k=0}^{m}|\beta _{k}|$

این روش تنظیم مدل که به روش لاسو (Lasso) نیز شهرت دارد باعث می‌شود که بسیاری از پارامترهای مدل نهائی صفر شوند و مدل به اصلاح خلوت (Sparse) شود.

در تنظیم مدل به روش $L_{2}$ تابع هزینه را به این شکل تغییر می‌دهیم:

$L_{r}(D,{\vec {\beta }})=L(D,{\vec {\beta }})+\lambda ||{\vec {\beta }}||_{2}^{2}=\sum _{i=1}^{n}({\vec {\beta }}\,.\,{\vec {x_{i}}}-y_{i})^{2}+\lambda \sum _{k=0}^{m}\beta _{k}^{2}$

در روش تنظیم از طریق $L_{2}$ سعی می‌شود طول اقلیدسی بردار ${\vec {\beta }}$ کوتاه نگه داشته شود. $\lambda$ در روش $L_{1}$ و $L_{2}$ یک عدد مثبت است که میزان تنظیم مدل را معین می‌کند. هرچقدر $\lambda$ کوچکتر باشد جریمه کمتری برا بزرگی نرم بردار پارامترها یعنی ${\vec {\beta }}$ پرداخت می‌کنیم. مقدار ایدئال $\lambda$ از طریق آزمایش بر روی داده اعتبار (Validation Data) پیدا می‌شود.

تفسیر احتمالی تنظیم مدل

اگر بجای روش درست نمایی بیشینه از روش بیشینه سازی احتمال پسین استفاده کنیم به ساختار «تنظیم مدل» یا همان regularization خواهیم رسید. اگر مجموعه داده را با $D$ نمایش بدهیم و پارامتری که به دنبال تخمین آن هستیم را با ${\vec {\beta }}$ ، احتمال پسین $Pr\left({\vec {\beta }}\,|\,D\right)$ ، طبق قانون بیز متناسب خواهد بود با حاصلضرب درست نمایی یعنی $Pr\left(D\,|\,{\vec {\beta }}\right)$ و احتمال پیشین یعنی $Pr\left({\vec {\beta }}\right)$ :

$Pr\left({\vec {\beta }}\,|\,D\right)={\frac {Pr\left(D\,|\,{\vec {\beta }}\right)\times Pr\left({\vec {\beta }}\right)}{Pr\left(D\right)}}$

ازین رو

$argmax_{\vec {\beta }}Pr\left({\vec {\beta }}\,|\,D\right)=argmax_{\vec {\beta }}{\frac {Pr\left(D\,|\,{\vec {\beta }}\right)\times Pr\left({\vec {\beta }}\right)}{Pr\left(D\right)}}=argmax_{\vec {\beta }}Pr\left(D\,|\,{\vec {\beta }}\right)\times Pr\left({\vec {\beta }}\right)$

معادله خط پیشین نشان می‌دهد که برای یافتن پارامتر بهینه فقط کافیست که احتمال پیشین را نیز در معادله دخیل کنیم. اگر احتمال پیشین را یک توزیع احتمال با میانگین صفر و کوواریانس $\tau ^{2}I$ در نظر بگیریم به معادله پایین می‌رسیم:

$argmax_{\vec {\beta }}\,\,\log Pr\left(D\,|\,{\vec {\beta }}\right)=argmax_{\vec {\beta }}\,\,\log \prod _{i=1}^{n}Pr(y_{i}|{\vec {x_{i}}}\,\,;{\vec {\beta }},\sigma )Pr\left({\vec {\beta }}\right)=argmax_{\vec {\beta }}\,\,\log \prod _{i=1}^{n}{\frac {1}{{\sqrt {2\pi }}\sigma }}exp\left(-{\frac {\left(y_{i}-{\vec {\beta }}\,.\,{\vec {x_{i}}}\right)^{2}}{2\sigma ^{2}}}\right){\frac {1}{{\sqrt {2\pi }}\tau }}exp\left(-{\frac {||{\vec {\beta }}||^{2}}{2\tau ^{2}}}\right)$

با ساده کردن این معادله به این جواب می‌رسیم، در اینجا $\lambda$ برابر است با ${\frac {\sigma ^{2}}{\tau ^{2}}}$ : $argmax_{\vec {\beta }}\,\,Pr\left(D\,|\,{\vec {\beta }}\right)=argmax_{\vec {\beta }}\left(n\log {\frac {1}{{\sqrt {2\pi }}\sigma }}-{\frac {1}{2\sigma ^{2}}}\sum _{i=1}^{n}\left(y_{i}-{\vec {\beta }}\,.\,{\vec {x_{i}}}\right)^{2}+\log {\frac {1}{{\sqrt {2\pi }}\tau }}-{\frac {1}{2\tau ^{2}}}||{\vec {\beta }}||^{2}\right)=argmin_{\vec {\beta }}\left(\sum _{i=1}^{n}\left(y_{i}-{\vec {\beta }}\,.\,{\vec {x_{i}}}\right)^{2}+\lambda ||{\vec {\beta }}||^{2}\right)$

همان‌طور که دیدیم جواب همان تنظیم مدل با نرم $L_{2}$ است.

حال اگر احتمال پیشین را از نوع توزیع لاپلاس با میانگین صفر درنظر بگیریم به تنظیم مدل با نرم $L_{1}$ خواهیم رسید.

منبع

استفاده از داده‌ها به منظور کشف رابطه بین آن‌ها اساس داده‌کاوی است. یکی از ابزار سنجش رابطه و مدل‌سازی استفاده از ابزار آماری رگرسیون است. امروزه به منظور تحلیل و کشف مدل روی «مه داده» (کلان‌داده | Big Data)، روش‌های مختلف رگرسیون توسعه یافته است. استفاده از تحلیل گرسیونی در علوم مختلف داده‌کاوی، بخصوص مبحث «آموزش ماشین» (Machine Learning)، فیزیک، شیمی و علوم زیستی کاربرد بسیاری دارد.

آگوست 24, 2019/0 دیدگاه /توسط hgadmin

تعریف رگرسیون خطی (Linear Regression) قسمت 2

آموزش عمومی پردازش تصویر و بینایی ماشین

تخمین پارامترها برای مسائل چند متغیره

صورت مسئله

در بسیاری از مسائل رایج رگرسیون ورودی چند متغیره هست. به عنوان مثال اگر فرض کنیم متغیر ما $m$ بُعد دارد، یعنی ${\vec {x}}=[x_{1},x_{2},\dots ,x_{m}]$ ، مسئله رگرسیون به یک مسئله بهینه‌سازی برای پیدا کردن $m+1$ پارامتر تبدیل می‌شود. به این معنی که ما یک پارامتر چند متغیره به اسم ${\vec {\beta }}=[\beta _{0},\beta _{1},\cdots ,\beta _{m}]$ داریم و سعی می‌کنیم که متغیر وابسته که همان $y$ است را با ترکیبی خطی از بردارد ورودیِ ${\vec {x}}$ ، تخمین بزنیم یعنی $y\approx \beta _{0}+\sum _{i=1}^{m}\beta _{i}\times x_{i}$ . حال اگر یک بعد دیگر به متغیر ${\vec {x}}$ اضافه کنیم و مقدارش را همیشه عدد ثابت $1$ در نظر بگیریم ( $x_{0}=1$ ) و ${\vec {x}}$ را به صورتِ ${\vec {x}}=[1,x_{1},x_{2},\dots ,x_{m}]$ تغییر دهیم، تخمینی که از $y$ داریم در واقع ضرب نقطه ای بردار ورودی و بردار پارامترهای ماست یعنی $y\approx \sum _{i=0}^{m}\beta _{i}\times x_{i}={\vec {\beta }}\,\,.\,{\vec {x}}$ . حال فرض کنیم که تعداد مثالهایی که قرار است برای تخمین پارامترها استفاده کنیم $n$ است و این مثالها را به این شکل نمایش دهیم $D=({\vec {x_{1}}},y_{1}),\cdots ({\vec {x_{n}}},y_{n})$ . پارامتر بهینه پارامتری است که یک تابع هزینه را به حداقل برساند و تخمینهایی ما را به متغیر وابسته بسیار نزدیک کند. تابع هزینه را با جمع مربع تفاضل تخمینها با متغیر وابسته تعریف می‌کنیم، به این شکل که $L(D,{\vec {\beta }})=\sum _{i=1}^{n}({\vec {\beta }}\,.\,{\vec {x_{i}}}-y_{i})^{2}$ ، با این حساب پارامتر بهینه می‌شود:

${\vec {\hat {\beta }}}=argmin_{\vec {\beta }}L(D,{\vec {\beta }})=argmin_{\vec {\beta }}\sum _{i=1}^{n}({\vec {\beta }}\,.\,{\vec {x_{i}}}-y_{i})^{2}$

تخمین پارامتر بهینه از روش کمترین مربعات

در این روش برای بدست آوردن ${\vec {\hat {\beta }}}$ یا همان پارامتر بهینه، از تابع $L(D,{\vec {\beta }})$ نسبت به ${\vec {\beta }}$ گرادیان می‌گیریم و گرادیان را برابر صفر قرار می‌دهیم و پارامتر بهینه را بدست می‌آوریم. از آنجا که تابع $L(D,{\vec {\beta }})$ نسبت به ${\vec {\beta }}$ تابعی کاملاً محدب است، در نقطه مینیمم گرادیان ما صفر خواهد بود و این روش پارامتر بهینه را بدست می‌دهد. برای تسهیل کار شکل تابع را با بکارگیری چند ماتریس ساده می‌کنیم. دو ماتریس برای این کار نیاز داردیم ماتریس $X$ و ماتریس $Y$ . ماتریس $X$ ماتریس ورودهای چندمتغیره ماست. هر سطر معادل یک نمونه از داده ماست، سطر $i$ ام برابر است با $i$ امین نمونه ورودی ما یعنی بردار ${\vec {x_{i}}}$ ، از اینرو $X$ یک ماتریس $n\times (m+1)$ خواهد بود. ماتریس $Y$ از طرف دیگر برابر است با مجموعه متغیرهای وابسته داده ما. سطر $i$ ام این ماتریس برابر است با متغیر وابسته برای $i$ امین نمونه داده ما یا همان $y_i$ . ماتریس $Y$ یک ماتریس $n\times 1$ است. با کمک این دو ماتریس می‌توان تابع هزینه را به شکل ذیل تعریف کرد:

$L(D,{\vec {\beta }})=||X{\vec {\beta }}-Y||^{2}=(X{\vec {\beta }}-Y)^{T}(X{\vec {\beta }}-Y)=Y^{T}Y-Y^{T}X{\vec {\beta }}-{\vec {\beta }}^{T}X^{T}Y+{\vec {\beta }}^{T}X^{T}X{\vec {\beta }}$

حال گرادیان این تابع را نسبت به ${\vec {\beta }}$ پیدا می‌کنیم که می‌شود:

${\frac {\partial L(D,{\vec {\beta }})}{\partial {\vec {\beta }}}}={\frac {\partial \left(Y^{T}Y-Y^{T}X{\vec {\beta }}-{\vec {\beta }}^{T}X^{T}Y+{\vec {\beta }}^{T}X^{T}X{\vec {\beta }}\right)}{\partial {\vec {\beta }}}}=-2X^{T}Y+2X^{T}X{\vec {\beta }}$

با برابر قرار دادن گرادیان با صفر پارامتر بهینه بدست می‌آید:

$-2X^{T}Y+2X^{T}X{\vec {\beta }}=0\Rightarrow X^{T}Y=X^{T}X{\vec {\beta }}\Rightarrow {\vec {\hat {\beta }}}=(X^{T}X)^{-1}X^{T}Y$

پس پارامتر بهینه ما برابر است با:

${\bf {{\vec {\hat {\beta }}}=(X^{T}X)^{-1}X^{T}Y}}$

تخمین پارامتر بهینه از روش گرادیان کاهشی تصادفی (Stochastic Gradient Descent)

روش پارامتر تخمین پارامتر بهینه از طریق کمترین مربعات ممکن است چند اشکال اساسی داشته باشد. یکی آنکه محاسبه $(X^{T}X)^{-1}$ ممکن است زمانبر باشد. بُعدِ ماتریس مربعی $X^{T}X$ برابر است با $(m+1)\times (m+1)$ و اگر بعد $m$ بالا باشد زمان محاسبه معکوس این ماتریس می‌تواند مسئله ساز شود. مضاف بر این، ماتریس ممکن است معکوس پذیر نباشد. از این رو روشهای کاراتر و سریعتری برای تخمین پارامتر بهینه مورد استفاده قرار می‌گیرد. یکی از این روشها روش گرادیان کاهشی تصادفی است. در این روش هر بار یک مثال را بصورت اتفاقی از نمونه‌های داده انتخاب کرده، گرادیان تابع هزینه را حساب می‌کنیم و کمی در جهت خلاف گرادیان پارامتر را حرکت می‌دهیم تا به یک پارامتر جدید برسیم. گرادیان جهت موضعی بیشترین افزایش را در تابع به ما نشان می‌دهد، برای بیشترین کاهش موضعی در خلاف جهت گرادیان باید حرکت کرد. اینکار را آنقدر ادامه می‌دهیم که گرادیان به اندازه کافی به صفر نزدیک شود. بجای اینکه داده‌ها را بصورت تصادفی انتخاب کنیم می‌توانیم به ترتیب داده شماره $1$ تا داده شماره $n$ را انتخاب کنیم و بعد دوباره به داده اولی برگردیم و این کار را چندین بار تکرار کنیم تا گرادیان تابع به اندازه کافی به صفر نزدیک شود. از لحاظ ریاضی این کار را می‌توان به شکل پایین انجام داد، پارامتر ${\vec {\beta }}$ را در ابتدا بصورت تصادفی مقدار دهی می‌کنیم و بعد برای داده $i$ ام و تمامی $j$ ‌ها، یعنی از $j=1$ تا $j=m+1$ تغییر پایین را اعمال می‌کنیم، دراینجا $\alpha$ همان مقداریست که در جهت گرادیان هربار حرکت می‌کنیم و $\left(y_{i}-{\vec {x_{i}}}.{\vec {\beta }}\right){\vec {x_{i,j}}}$ مشتق جزئی داده $i$ ام در بُعد $j$ ام است:

${\begin{cases}{\mbox{Initialize}}\,\,{\vec {\beta ^{\,old}}}\,\,{\mbox{randomly}}\\{\mbox{loop until convergence :}}\\\,\,{\mbox{for}}\,\,\,\,i=0\,\,\,\,{\mbox{to}}\,\,\,\,n:\\\,\,\,\,\,\,{\mbox{for}}\,\,\,\,j=0\,\,\,\,{\mbox{to}}\,\,\,\,m:\\\,\,\,\,\,\,\,\,\,\,\,\,{\vec {\beta _{j}^{\,new}}}={\vec {\beta _{j}^{\,old}}}+\alpha \left(y_{i}-{\vec {\beta ^{\,old}}}\,.\,{\vec {x_{i}}}\right){\vec {x_{i,j}}}\\\,\,\,\,\,\,\beta ^{\,old}=\beta ^{\,new}\end{cases}}$

تفسیر احتمالی از طریق درست نمایی بیشینه

برای بدست آوردن پارامتر بهینه ${\vec {\hat {\beta }}}$ تابع هزینه یعنی $L(D,{\vec {\beta }})$ را به حداقل می‌رسانیم. می‌توان به همین پارامتر بهینه از روش درست نمایی بیشینه هم رسید. فرض می‌کنیم که متغیر وابسته یعنی $y$ یک متغیر تصادفی است که مقدارش از یک توزیع طبیعی (توزیع گاوسی) پیروی می‌کند. این توزیع احتمال، واریانس ثابتی به اسم $\sigma$ دارد ولی میانگین آن ترکیبی خطی از متغیرهای مستقل یعنی ${\vec {x}}=[1,x_{1},x_{2},\dots ,x_{m}]$ است. به عبارت دیگر میانگین ما برابر است با ${\vec {\beta }}\,.\,{\vec {x}}$ . با احتساب میانگین و واریانس توزیع متغیر وابسته ما می‌شود $y\sim N({\vec {\beta }}\,.\,{\vec {x}},\sigma )$ . حال اگر فرض کنیم داده‌های ما نسبت به هم مستقل هستند تابع درست نمایی برای تمام داده‌ها می‌شود:

$H(D,{\vec {\beta }})=\prod _{i=1}^{n}Pr(y_{i}|{\vec {x_{i}}}\,\,;{\vec {\beta }},\sigma )=\prod _{i=1}^{n}{\frac {1}{{\sqrt {2\pi }}\sigma }}exp\left(-{\frac {\left(y_{i}-{\vec {\beta }}\,.\,{\vec {x_{i}}}\right)^{2}}{2\sigma ^{2}}}\right)$

حال باید به دنبال پارامتری باشیم که این تابع بزرگنمایی را بیشینه کند. از آنجا که تابع لگاریتم مطلقاً صعودیست، بجای بیشینه کردن این تابع لگاریتمش را هم می‌شود بیشنه کرد و پارامتر بهینه را از آن طریق پیدا کرد:

$I(D,{\vec {\beta }})=\log \prod _{i=1}^{n}Pr(y_{i}|{\vec {x_{i}}}\,\,;{\vec {\beta }},\sigma )=\log \prod _{i=1}^{n}{\frac {1}{{\sqrt {2\pi }}\sigma }}exp\left(-{\frac {\left(y_{i}-{\vec {\beta }}\,.\,{\vec {x_{i}}}\right)^{2}}{2\sigma ^{2}}}\right)=n\log {\frac {1}{{\sqrt {2\pi }}\sigma }}-{\frac {1}{2\sigma ^{2}}}\sum _{i=1}^{n}\left(y_{i}-{\vec {\beta }}\,.\,{\vec {x_{i}}}\right)^{2}$

پارامتر بهینه از این طریق برابر است با:

$argmax_{\vec {\beta }}I(D,{\vec {\beta }})=argmax_{\vec {\beta }}\left(n\log {\frac {1}{{\sqrt {2\pi }}\sigma }}-{\frac {1}{2\sigma ^{2}}}\sum _{i=1}^{n}\left(y_{i}-{\vec {\beta }}\,.\,{\vec {x_{i}}}\right)^{2}\right)=argmin_{\vec {\beta }}\sum _{i=1}^{n}\left(y_{i}-{\vec {\beta }}\,.\,{\vec {x_{i}}}\right)^{2}=argmin_{\vec {\beta }}L(D,{\vec {\beta }})={\vec {\hat {\beta }}}$

همان‌طور که دیدم پارامتری که $I(D,{\vec {\beta }})$ را بیشینه می‌کند همان پارامتری است که $L(D,{\vec {\beta }})$ را به حداقل می‌رساند. این به معنی معادل بودن روش کمترین مربعات با روش درست نمایی بیشنه در رگرسیون خطی است.

آگوست 24, 2019/0 دیدگاه /توسط hgadmin

تعریف رگرسیون خطی (Linear Regression) قسمت 1

آموزش عمومی پردازش تصویر و بینایی ماشین

رگرسیون خطی یا تنازل خطی یا وایازی خطی (Linear regression) یکی از روشهای تحلیل رگرسیون است. در رگرسیون خطی، متغیّر وابسته $y$ ترکیب خطی‌ای از ورودی یا متغیرهای مستقل است. البته ضرورتاً متغیر وابسته لازم نیست که نسبت به متغیرهای مستقل، خطی باشد.

رگرسیون خطی با یک متغیر مستقل

تخمین پارامترها برای مسائل تک متغیره

رگرسیون میزان اثر دو یا چند متغیر بر متغیر وابسته را می‌سنجد و همبستگی رابطه بین دو یا چند متغیر را مورد سنجش قرار می‌دهد.

مثلاً تحلیل رگرسیونی سادهٔ زیر با $N$ نقطه، متغیر مستقل $x_i$ و ضرایب $\beta _{0}$ و $\beta _{1}$ خطی است:

خط راست:

y_{i}=\beta _{0}+\beta _{1}x_{i}+\epsilon _{i},\quad i=1,\dots ,N\!

در هر دو حالت، $\epsilon _{i}$ مقدار خطاست و پانویس $i$ شمارهٔ هر مشاهده (هر جفت $x_i$ و $y_i$ ) را نشان می‌دهد. با داشتن مجموعه‌ای از این نقطه‌ها می‌توان مدل را به دست آورد:

y_{i}={\widehat {\beta }}_{0}+{\widehat {\beta }}_{1}X_{i}+e_{i}

عبارت $e_{i}$ مانده نام دارد: $e_{i}=y_{i}-{\widehat {y}}_{i}$ . روش رایج برای به‌دست‌آوردن پارامترها، روش کمترین مربعات است. در این روش پارامترها را با کمینه‌کردن تابع زیر به دست می‌آورند:

\mathrm {SSE} =\sum _{i=1}^{N}e_{i}^{2}

در مورد رگرسیون ساده، پارامترها با این روش برابر خواهند بود با:

{\widehat {\beta _{1}}}={\frac {\sum (x_{i}-{\bar {x}})(y_{i}-{\bar {y}})}{\sum (x_{i}-{\bar {x}})^{2}}}

{\hat {\beta _{0}}}={\bar {y}}-{\widehat {\beta _{1}}}{\bar {x}}

که در آن ${\bar {x}}$ و ${\bar {y}}$ میانگین $x$ و $y$ هستند.

تفاوت رگرسیون و همبستگی بر اساس هدف:

هدف مدل‌های همبستگی بررسی میزان رابطه دو یا چند متغیر است در حالیکه رگرسیون به دنبال پیش‌بینی یک یا چند متغیر براساس یک یا چند متغیر دیگر است. از آنجا که رگرسیون برپایه داده‌های گذشته انجام می‌شود به آن عنوان Regression یعنی بازگشت به گذشته داده‌اند؛ بنابراین از نظر هدف همبستگی میزان و شدت رابطه متغیرها را نشان می‌دهد اما رگرسیون معادله ای را برای پیش‌بینی متغیرها ارائه می‌کند.

تفاوت رگرسیون و همبستگی براساس روش:

آنچه در خروجی نتایج رگرسیون و همبستگی باعث ایجاد تفاوت می‌شود آن است که در همبستگی همیشه اثرات متغیرها به صورت دو به دو مورد سنجش قرار می‌گیرد اما در یک مدل رگرسیون اثرات متغیرها به صورت همزمان بررسی می‌شود. یعنی در همبستگی رابطه متغیر X با متغیر Y به وجود یا عدم وجود متغیر Z ارتباطی ندارد اما اما در رگرسیون تأثیر متغیر X بر متغیر Y به وجود یا عدم وجود متغیر Z بستگی دارد.

آگوست 24, 2019/0 دیدگاه /توسط daliri

مشخصات فنی دوربین پلاک‌خوان معاینه فنی

وبلاگ

مشخصات فنی دوربین های پلاک‌خوان جهت نصب در مراکز خدمات فنی مجاز اتحادیه کشوری سوخت های جایگزین و خدمات وابسته، به شرح زیر اعلام شد.

جهت خریداری توجه داشته باشید، دوربین مورد نظر شرایط فنی زیر را دارا باشد.

مشخصات فنی دوربین های پلاک‌خوان مراکز معاینه فنی
1/2.8 cmos – 2 mp Full HD	Image sensor
Color: 0/1 lox – B/w: 0/1 lox	Min illumination
1s~1/10,000s	Minshutter time
P-Iris	Auto Iris
IR cut filter with auto switch	Day & Night
DNR	Digital noise reduction
True – 120 dB Real	Wide dynamic range
H.264-MPEG4-MJPEG	Video compression
UP TO 1920*1080	Resolution
UP TO 30 fps at (1920*1080)	Frame Rate
-30 °C ~ 55 °C – Humidity 100%	Operating conditions
At least one zone configurable	Rol
Yes	HLC
Yes	BLC
Yes	Defog
Yes	ELC
Yes	Smart Focus
Yes	Network Interface
User Authentication, anonymous access	Security
ONVIF (Profile S, Profile G)	System Compatibility
PoE	Power Supply
Import/Export configuration capability – rese buttom – web broeser access	Other feature
Varifocal P-Iris	Lens Type
Under the terms of Iris	Focal Length
IP66	Housing

منبع

آگوست 23, 2019/2 دیدگاه /توسط BehsanAndish

تعریف فیلتر کالمن (Kalman filter) قسمت 2

آموزش عمومی پردازش تصویر و بینایی ماشین

بخت حاشیه‌ای

همانند تخمین بازگشتی بیز که پیش‌تر بیان شد، فیلتر کالمن را می‌توان به عنوان یک مدل مولد دید. یعنی فرایندی برای تولید دنباله‌ای از مشاهدات تصادفی (… ,z = (z₀, z₁, z_2. این فرایند به صورت زیر تعریف می‌شود:

حالت پنهان $\mathbf {x} _{0}$ را از توزیع گاوسی پیشین $p(\mathbf {x} _{0})={\mathcal {N}}({\hat {\mathbf {x} }}_{0\mid 0},\mathbf {P} _{0\mid 0})$ نمونه‌گیری کنید.
حالت پنهان $\mathbf {x} _{0}$ $\mathbf {z} _{0}$ را از مدل مشاهده شده $p(\mathbf {z} _{0}\mid \mathbf {x} _{0})={\mathcal {N}}(\mathbf {H} _{0}\mathbf {x} _{0},\mathbf {R} _{0})$ نمونه‌گیری کنید.
برای $k=1,2,3,\ldots$
1. حالت پنهان $\mathbf {x} _{k}$ را از مدل انتقالی $p(\mathbf {x} _{k}\mid \mathbf {x} _{k-1})={\mathcal {N}}(\mathbf {F} _{k}\mathbf {x} _{k-1}+\mathbf {B} _{k}\mathbf {u} _{k},\mathbf {Q} _{k})$ محاسبه کنید.
2. مشاهده $\mathbf {z} _{k}$ را از مدل مشاهده شده $p(\mathbf {z} _{k}\mid \mathbf {x} _{k})={\mathcal {N}}(\mathbf {H} _{k}\mathbf {x} _{k},\mathbf {R} _{k})$ محاسبه کنید.

این فرایند ساختاری مشابه مدل پنهان مارکوف دارد که حالات گسسته در آن به متغیرهای تصادفی پیوسته با توزیع گاوسی تبدیل شده‌است.

محاسبه بخت حاشیه‌ای به عنوان نتیجه‌ای از فیلتر کردن بازگشتی بسیار آسان است. به کمک قانون زنجیره‌ای احتمال، بخت از حاصلضرب احتمال هر مشاهده به شرط مشاهدات قبلی بدست می‌آید،

$p(\mathbf {z} )=\prod _{k=0}^{T}p(\mathbf {z} _{k}\mid \mathbf {z} _{k-1},\ldots ,\mathbf {z} _{0})$

به علاوه چون فیلتر کالمن معرف یک فرایند مارکوف است، تمام دانش بدست آمده از مشاهدات قبلی به تخمین ${\hat {\mathbf {x} }}_{k\mid k-1},\mathbf {P} _{k\mid k-1}$ محدود می‌شود. به این ترتیب بخت حاشیه‌ای به صورت زیر محاسبه می‌شود:

${\begin{aligned}p(\mathbf {z} )&=\prod _{k=0}^{T}\int p(\mathbf {z} _{k}\mid \mathbf {x} _{k})p(\mathbf {x} _{k}\mid \mathbf {z} _{k-1},\ldots ,\mathbf {z} _{0})d\mathbf {x} _{k}\\&=\prod _{k=0}^{T}\int {\mathcal {N}}(\mathbf {z} _{k};\mathbf {H} _{k}\mathbf {x} _{k},\mathbf {R} _{k}){\mathcal {N}}(\mathbf {x} _{k};{\hat {\mathbf {x} }}_{k\mid k-1},\mathbf {P} _{k\mid k-1})d\mathbf {x} _{k}\\&=\prod _{k=0}^{T}{\mathcal {N}}(\mathbf {z} _{k};\mathbf {H} _{k}{\hat {\mathbf {x} }}_{k\mid k-1},\mathbf {R} _{k}+\mathbf {H} _{k}\mathbf {P} _{k\mid k-1}\mathbf {H} _{k}^{T})\\&=\prod _{k=0}^{T}{\mathcal {N}}(\mathbf {z} _{k};\mathbf {H} _{k}{\hat {\mathbf {x} }}_{k\mid k-1},\mathbf {S} _{k})\end{aligned}}$

رابطه بالا حاصلضرب چند توزیع احتمال گاوسی است که هر یک نمایانگر یک مشاهده z_k تحت فیلتر $\mathbf {H} _{k}{\hat {\mathbf {x} }}_{k\mid k-1},\mathbf {S} _{k}$ است؛ که از آپدیت‌های بازگشتی محاسبه می‌شود. برای راحتی محاسبه بهتر است از log بخت حاشیه‌ای یعنی $\ell =\log p(\mathbf {z} )$ استفاده شود. با فرض $\ell ^{(-1)}=0$ محاسبه به صورت بازگشتی انجام می‌شود.

$\ell ^{(k)}=\ell ^{(k-1)}-{\frac {1}{2}}\left({\tilde {\mathbf {y} }}_{k}^{T}\mathbf {S} _{k}^{-1}{\tilde {\mathbf {y} }}_{k}+\log \left|\mathbf {S} _{k}\right|+d_{y}\log 2\pi \right)$

به‌طوری‌که $d_{y}$ بعد بردار اندازه‌گیری‌ها می‌باشد.

فیلتر اطلاعاتی

در فیلتر اطلاعاتی یا فیلتر کوواریانس معکوس، تخمین کوواریانس و تخمین حالت به ترتیب با ماتریس اطلاعات و تابع اطلاعات جایگزین می‌شوند.

{\textbf {Y}}_{k\mid k}={\textbf {P}}_{k\mid k}^{-1}

{\hat {\textbf {y}}}_{k\mid k}={\textbf {P}}_{k\mid k}^{-1}{\hat {\textbf {x}}}_{k\mid k}

به طریق مشابه کوواریانس و بردار مشاهدات هم با عبارات هم‌ارز اطلاعاتی جایگزین می‌شوند.

{\textbf {Y}}_{k\mid k-1}={\textbf {P}}_{k\mid k-1}^{-1}

{\hat {\textbf {y}}}_{k\mid k-1}={\textbf {P}}_{k\mid k-1}^{-1}{\hat {\textbf {x}}}_{k\mid k-1}

با داشتن ماتریس و بردار مشاهدات که به صورت زیر تعریف شده‌اند

{\textbf {I}}_{k}={\textbf {H}}_{k}^{\text{T}}{\textbf {R}}_{k}^{-1}{\textbf {H}}_{k}

{\textbf {i}}_{k}={\textbf {H}}_{k}^{\text{T}}{\textbf {R}}_{k}^{-1}{\textbf {z}}_{k}

اطلاعات آپدیت شده به صورت زیر نوشته می‌شوند.

{\textbf {Y}}_{k\mid k}={\textbf {Y}}_{k\mid k-1}+{\textbf {I}}_{k}

{\hat {\textbf {y}}}_{k\mid k}={\hat {\textbf {y}}}_{k\mid k-1}+{\textbf {i}}_{k}

مزیت اصلی فیلتر اطلاعاتی این است که N مشاهده می‌توانند در هر بازه زمانی با جمع زدن ماتریس‌ها و بردارهای اطلاعاتی فیلتر شوند.

{\textbf {Y}}_{k\mid k}={\textbf {Y}}_{k\mid k-1}+\sum _{j=1}^{N}{\textbf {I}}_{k,j}

{\hat {\textbf {y}}}_{k\mid k}={\hat {\textbf {y}}}_{k\mid k-1}+\sum _{j=1}^{N}{\textbf {i}}_{k,j}

جهت پیش‌بینی فیلتر اطلاعات ماتریس و بردار اطلاعات به عبارات هم‌ارزشان در فضای حالات سیستم تبدیل می‌شوند. البته پیش‌بینی فضای اطلاعاتی هم قابل انجام است.

{\textbf {M}}_{k}=[{\textbf {F}}_{k}^{-1}]^{\text{T}}{\textbf {Y}}_{k-1\mid k-1}{\textbf {F}}_{k}^{-1}

{\textbf {C}}_{k}={\textbf {M}}_{k}[{\textbf {M}}_{k}+{\textbf {Q}}_{k}^{-1}]^{-1}

{\textbf {L}}_{k}=I-{\textbf {C}}_{k}

{\textbf {Y}}_{k\mid k-1}={\textbf {L}}_{k}{\textbf {M}}_{k}{\textbf {L}}_{k}^{\text{T}}+{\textbf {C}}_{k}{\textbf {Q}}_{k}^{-1}{\textbf {C}}_{k}^{\text{T}}

{\hat {\textbf {y}}}_{k\mid k-1}={\textbf {L}}_{k}[{\textbf {F}}_{k}^{-1}]^{\text{T}}{\hat {\textbf {y}}}_{k-1\mid k-1}

این مقادیر به شرطی قابل محاسبه‌اند که F و Q در زمان ثابت باشند. همچنینF و Q باید معکوس‌پذیر باشند.

تصفیه‌کننده تأخیر زمانی

تصفیه‌کننده بهینه تخمینی بهینه از ${\hat {\textbf {x}}}_{k-N\mid k}$ برای تأخیر ثابت $N$ با استفاده از مشاهدات ${\textbf {z}}_{1}$ تا ${\textbf {z}}_{k}$ ارائه می‌کند. این تخمین به کمک روابط قبلی و برای یک حالت تکمیل شده به صورت زیر بدست می‌آید:

${\begin{bmatrix}{\hat {\textbf {x}}}_{t\mid t}\\{\hat {\textbf {x}}}_{t-1\mid t}\\\vdots \\{\hat {\textbf {x}}}_{t-N+1\mid t}\\\end{bmatrix}}={\begin{bmatrix}{\textbf {I}}\\0\\\vdots \\0\\\end{bmatrix}}{\hat {\textbf {x}}}_{t\mid t-1}+{\begin{bmatrix}0&\ldots &0\\{\textbf {I}}&0&\vdots \\\vdots &\ddots &\vdots \\0&\ldots &I\\\end{bmatrix}}{\begin{bmatrix}{\hat {\textbf {x}}}_{t-1\mid t-1}\\{\hat {\textbf {x}}}_{t-2\mid t-1}\\\vdots \\{\hat {\textbf {x}}}_{t-N+1\mid t-1}\\\end{bmatrix}}+{\begin{bmatrix}{\textbf {K}}^{(0)}\\{\textbf {K}}^{(1)}\\\vdots \\{\textbf {K}}^{(N-1)}\\\end{bmatrix}}{\textbf {y}}_{t\mid t-1}$

به‌طوری‌که:

${\hat {\textbf {x}}}_{t\mid t-1}$ و ${\textbf {y}}_{t\mid t-1}={\textbf {z}}_{t}-{\textbf {H}}{\hat {\textbf {x}}}_{t\mid t-1}$ با یک فیلتر استاندارد کالمن تخمین زده شده‌است.
${\hat {\textbf {x}}}_{t-i\mid t}$ و $i=1,\ldots ,N-1$ متغیرهای جدیدی هستند که در فیلتر کالمن وجود نداشتند.
نتایج کالمن از رابطه زیر بدست می‌آیند:
- ${\textbf {K}}^{(i)}={\textbf {P}}^{(i)}{\textbf {H}}^{T}\left[{\textbf {H}}{\textbf {P}}{\textbf {H}}^{\mathrm {T} }+{\textbf {R}}\right]^{-1}$
- ${\textbf {P}}^{(i)}={\textbf {P}}\left[\left[{\textbf {F}}-{\textbf {K}}{\textbf {H}}\right]^{T}\right]^{i}$

به‌طوری‌که ${\textbf {P}}$ و ${\textbf {K}}$ کوواریانس خطاهای پیش‌بینی شده و نتایج فیلتر استاندارد کالمن هستند. ( ${\textbf {P}}_{t\mid t-1}$ )

اگر تخمین کوواریانس خطا را به صورت زیر تعریف کنیم:

${\textbf {P}}_{i}:=E\left[\left({\textbf {x}}_{t-i}-{\hat {\textbf {x}}}_{t-i\mid t}\right)^{*}\left({\textbf {x}}_{t-i}-{\hat {\textbf {x}}}_{t-i\mid t}\right)\mid z_{1}\ldots z_{t}\right]$

تخمین بهتری از ${\textbf {x}}_{t-i}$ از رابطه زیر حاصل می‌شود.

${\textbf {P}}-{\textbf {P}}_{i}=\sum _{j=0}^{i}\left[{\textbf {P}}^{(j)}{\textbf {H}}^{T}\left[{\textbf {H}}{\textbf {P}}{\textbf {H}}^{\mathrm {T} }+{\textbf {R}}\right]^{-1}{\textbf {H}}\left({\textbf {P}}^{(i)}\right)^{\mathrm {T} }\right]$

تصفیه‌کننده بازه

تصفیه‌کننده بهینه تخمینی بهینه از ${\hat {\textbf {x}}}_{k\mid n}$ ( $k<n$ ) با استفاده از مشاهداتی در بازه ${\textbf {z}}_{1}$ تا ${\textbf {z}}_{n}$ ارائه می‌کند. به این مبحث «تصفیه‌کننده کالمن» هم گفته می‌شود. الگوریتم‌های مختلفی با این منظور موجودند.

Rauch–Tung–Striebel

الگوریتمی دو مرحله‌ای و کارا برای تصفیه کردن بازه است. گام رو به جلو مشابه فیلتر عادی کالمن است. تخمین‌های فیلتر شده پیشین و پسین ${\hat {\textbf {x}}}_{k\mid k-1}$ ، ${\hat {\textbf {x}}}_{k\mid k}$ و ${\textbf {P}}_{k\mid k-1}$ ، ${\textbf {P}}_{k\mid k}$ در گام رو به عقب کاربرد دارند.

در گام رو به عقب تخمین تصفیه‌شده ${\hat {\textbf {x}}}_{k\mid n}$ و ${\textbf {P}}_{k\mid n}$ را محاسبه می‌کنیم. بدین طریق که از آخرین بازه زمانی شروع کرده و به صورت عقب‌گرد معادلات بازگشتی زیر را می‌یابیم:

{\hat {\textbf {x}}}_{k\mid n}={\hat {\textbf {x}}}_{k\mid k}+{\textbf {C}}_{k}({\hat {\textbf {x}}}_{k+1\mid n}-{\hat {\textbf {x}}}_{k+1\mid k})

{\textbf {P}}_{k\mid n}={\textbf {P}}_{k\mid k}+{\textbf {C}}_{k}({\textbf {P}}_{k+1\mid n}-{\textbf {P}}_{k+1\mid k}){\textbf {C}}_{k}^{\mathrm {T} }

به‌طوری‌که

{\textbf {C}}_{k}={\textbf {P}}_{k\mid k}{\textbf {F}}_{k+1}^{\mathrm {T} }{\textbf {P}}_{k+1\mid k}^{-1}

{\textbf {x}}_{k\mid k}

تخمین حالت پسین زمان

k

\mathbf {x} _{k+1\mid k}

تخمین حالت پیشین زمان

k+1

است. درمورد کوواریانس نیز همین نوشتار به کار می‌رود.

تصفیه‌کننده Bryson–Frazier

این روش جایگزینی برای الگوریتم RTS است که توسط بیرمن ارائه شده‌است. این روش همچنین در گام رو به عقب داده‌های بدست آمده در گام رو به جلوی فیلتر کالمن استفاده می‌کند. معادلات رو به عقب شامل محاسبات بازگشتی که پس از هر مشاهده جهت تصفیه حالت و کوواریانس به کار برده می‌شود.

معادلات بازگشتی عبارتند از:

{\tilde {\Lambda }}_{k}={\textbf {H}}_{k}^{T}{\textbf {S}}_{k}^{-1}{\textbf {H}}_{k}+{\hat {\textbf {C}}}_{k}^{T}{\hat {\Lambda }}_{k}{\hat {\textbf {C}}}_{k}

{\hat {\Lambda }}_{k-1}={\textbf {F}}_{k}^{T}{\tilde {\Lambda }}_{k}{\textbf {F}}_{k}

{\hat {\Lambda }}_{n}=0

{\tilde {\lambda }}_{k}=-{\textbf {H}}_{k}^{T}{\textbf {S}}_{k}^{-1}{\textbf {y}}_{k}+{\hat {\textbf {C}}}_{k}^{T}{\hat {\lambda }}_{k}

{\hat {\lambda }}_{k-1}={\textbf {F}}_{k}^{T}{\tilde {\lambda }}_{k}

{\hat {\lambda }}_{n}=0

به‌طوری‌که ${\textbf {S}}_{k}$ کوواریانس باقیمانده‌است و ${\hat {\textbf {C}}}_{k}={\textbf {I}}-{\textbf {K}}_{k}{\textbf {H}}_{k}$ . همچنین حالت و کوواریانس تصفیه‌شده با کمک معادلات زیر قابل محاسبه است.

{\textbf {P}}_{k\mid n}={\textbf {P}}_{k\mid k}-{\textbf {P}}_{k\mid k}{\hat {\Lambda }}_{k}{\textbf {P}}_{k\mid k}

{\textbf {x}}_{k\mid n}={\textbf {x}}_{k\mid k}-{\textbf {P}}_{k\mid k}{\hat {\lambda }}_{k}

یا

{\textbf {P}}_{k\mid n}={\textbf {P}}_{k\mid k-1}-{\textbf {P}}_{k\mid k-1}{\tilde {\Lambda }}_{k}{\textbf {P}}_{k\mid k-1}

{\textbf {x}}_{k\mid n}={\textbf {x}}_{k\mid k-1}-{\textbf {P}}_{k\mid k-1}{\tilde {\lambda }}_{k}.

از مزیت‌های MBF عدم نیاز به یافتن معکوس ماتریس کوواریانس است.

تصفیه‌کننده کمینه واریانس

این روش می‌تواند بهترین خطای ممکن را با استفاده از پارامترها و آماره‌های نویزی شناخته‌شده بدست آورد. این تصفیه‌کننده مدل کلی‌تری از فیلتر غیر علی وینر است. (non-causal Wiener filter)

محاسبات در دو گام انجام می‌شود. محاسبات گام رو به جلو در یک مرحله پیش‌بینی صورت می‌گیرد:

{\hat {\textbf {x}}}_{k+1\mid k}={\textbf {(F}}_{k}-{\textbf {K}}_{k}{\textbf {H}}_{k}){\hat {\textbf {x}}}_{k\mid k-1}+{\textbf {K}}_{k}{\textbf {z}}_{k}

{\alpha }_{k}=-{\textbf {S}}_{k}^{-1/2}{\textbf {H}}_{k}{\hat {\textbf {x}}}_{k\mid k-1}+{\textbf {S}}_{k}^{-1/2}{\textbf {z}}_{k}

این عبارات معکوس وینر-هوف (Wiener-Hopf) است. نتیجه گام رو به عقب $\beta _{k}$ می‌تواند با استفاده بازگشت در زمان و از گام رو به جلو از $\alpha _{k}$ محاسبه شود. در این حالت خروجی سیستم برابر است با:

${\hat {\textbf {y}}}_{k\mid N}={\textbf {z}}_{k}-{\textbf {R}}_{k}\beta _{k}$

با جایگذاری در رابطه بالا

${\hat {\textbf {y}}}_{k\mid k}={\textbf {z}}_{k}-{\textbf {R}}_{k}{\textbf {S}}_{k}^{-1/2}\alpha _{k}$

این معادله برا ی فیلتر کالمن کمینه واریانس همواره یکسان است. حل معادلات بالا واریانس تخمین خطای خروجی را کمینه می‌کند. توجه کنید که در روش Rauch–Tung–Striebel فرض می‌شود که همه توزیع‌ها گاوسی هستند اما در اینجا چنین نیست.

فیلترهای وزن‌دار کالمن

توابع وزن‌دار جهت وزن دادن به میانگین توزیع توان خطا در یک بازه تغییر مشخص استفاده می‌شوند. فرض کنید ${\textbf {y}}$ – ${\hat {\textbf {y}}}$ یک تخمین خطای خروجی توسط فیلتر کالمن و ${\textbf {W}}$ یک تابع تخصیص وزن علی باشد. روش بهینه‌ای که واریانس ( ${\textbf {y}}$ – ${\hat {\textbf {y}}}$ ) ${\textbf {W}}$ را کمینه می‌کند استفاده از ${\textbf {W}}^{-1}{\hat {\textbf {y}}}$ است.

نحوه طراحی ${\textbf {W}}$ فعلاً بی‌پاسخ است. یک راه آن شناسایی سیستمی که تخمین خطا را تولید می‌کند و قرارداد کردن ${\textbf {W}}$ به عنوان معکوس آن سیستم است. این روش می‌تواند جهت محاسبه خطای مربع میانگین استفاده شود تا هزینه فیلتر کاهش یابد. همچنین روش مشابهی جهت یافتن تصفیه‌کننده نیز وجود دارد.

فیلترهای غیرخطی

مبنای فیلتر کالمن، تبدیلات خطی است. اما سیستم‌های پیچیده‌تر می‌توانند غیرخطی باشند. مسئله غیرخطی بودن می‌تواند در مشاهدات، مدلسازی یا هر دو بروز پیدا کند.

فیلتر کالمن بسط‌یافته – EKF

در فیلتر بسط‌یافته کالمن (EKF) انتقال حالات و مشاهدات نیاز به توابع حالت خطی یا غیرخطی دارند. اینها توابعی مشتق‌پذیر هستند.

{\textbf {x}}_{k}=f({\textbf {x}}_{k-1},{\textbf {u}}_{k})+{\textbf {w}}_{k}

{\textbf {z}}_{k}=h({\textbf {x}}_{k})+{\textbf {v}}_{k}

تابع f می‌تواند جهت محاسبه حالت پیش‌بینی شده از تخمین قبلی به کار رود. همچنین تابع h جهت یافتن مشاهده‌ای از حالت قبلی به کار می‌رود. توابع f و h نمی‌توانند مستقیماً به کوواریانس اعمال شوند، بلکه باید ماتریسی از مشتقات جزیی (ماتریس ژاکوبی) آن‌ها محاسبه شود.

در هر بازه زمانی ماتریس ژاکوبی با استفاده از حالات پیش‌بینی شده قبلی محاسبه می‌شود. این ماتریس‌ها در معادلات فیلتر کالمن کاربرد دارد. در واقع این فرایند عمل خطی کردن توابع غیرخطی را حول تخمین فعلی شامل می‌شود.

فیلتر کالمن از نوع UKF – Unscented

وقتی انتقال حالات و مشاهدات، یعنی توابع پیش‌بینی و آپدیت $f$ و $h$ ، کاملاً غیرخطی باشند، فیلتر کالمن بسط‌یافته کارایی پایینی خواهد داشت. به این دلیل که کوواریانس در عمل خطی‌سازی مدل غیرخطی افزایش می‌یابد. فیلتر کالمن Unscented از روش نمونه‌گیری قطعی که به Uncented Transform معروف است، استفاده می‌کند تا مجموعه نمونه مینیمالی از نقاط حول میانگین را جمع‌آوری کند. سپس این نقاط در تابع غیرخطی وارد شده تا میانگین و کوواریانس جدید حاصل شود. نتیجه برای سیستم‌های قطعی با قطعیت بیشتری مقدار میانگین و کوواریانس را ارائه می‌کند.^[۳۰]این روش به عنوان روش مونت‌کارلو یا بسط تیلور برای آماره‌های پسین شناخته شده‌است. در واقع این روش ما را از محاسبه مستقیم ماتریس ژاکوبی که برای بعضی توابع بسیار پیچیده‌است، بی‌نیاز می‌کند.

پیش‌بینی

مشابه EKF، در روش UKF فاز پیش‌بینی در مقایسه با یک آپدیت خطی مستقل از آپدیت UKF انجام می‌شود. تخمین حالت و کوواریانس با کمک میانگین و کوواریانس فرایند بدست می‌آیند.

{\textbf {x}}_{k-1\mid k-1}^{a}=[{\hat {\textbf {x}}}_{k-1\mid k-1}^{\mathrm {T} }\quad E[{\textbf {w}}_{k}^{\mathrm {T} }]\ ]^{\mathrm {T} }

{\textbf {P}}_{k-1\mid k-1}^{a}={\begin{bmatrix}&{\textbf {P}}_{k-1\mid k-1}&&0&\\&0&&{\textbf {Q}}_{k}&\end{bmatrix}}

مجموعه‌ای شامل 2L + ۱ به کمک حالت و کوواریانس از حالت بعد L حاصل می‌شود.

\chi _{k-1\mid k-1}^{0}={\textbf {x}}_{k-1\mid k-1}^{a}

\chi _{k-1\mid k-1}^{i}={\textbf {x}}_{k-1\mid k-1}^{a}+\left({\sqrt {(L+\lambda ){\textbf {P}}_{k-1\mid k-1}^{a}}}\right)_{i},\qquad i=1,\ldots ,L

\chi _{k-1\mid k-1}^{i}={\textbf {x}}_{k-1\mid k-1}^{a}-\left({\sqrt {(L+\lambda ){\textbf {P}}_{k-1\mid k-1}^{a}}}\right)_{i-L},\qquad i=L+1,\dots {},2L

به‌طوری‌که

\left({\sqrt {(L+\lambda ){\textbf {P}}_{k-1\mid k-1}^{a}}}\right)_{i}

iامین ستون ماتریس مربع ریشه $(L+\lambda ){\textbf {P}}_{k-1\mid k-1}^{a}$ است.

با توجه به تعریف ریشه مربعی ${\textbf {A}}$ در ماتریس ${\textbf {B}}$ بدست می‌آید:

${\textbf {B}}\triangleq {\textbf {A}}{\textbf {A}}^{\mathrm {T} }\,$

ریشه مربعی باید به صورت عددی و توسط روش‌هایی مانند تفکیک کولسکی محاسبه شود.

نقاط بدست آمده به عنوان ورودی تابع انتقال f داده می‌شوند:

$\chi _{k\mid k-1}^{i}=f(\chi _{k-1\mid k-1}^{i})\quad i=0,\dots ,2L$

به‌طوری‌که $f:R^{L}\rightarrow R^{|{\textbf {x}}|}$ . از نقاط وزن‌دار جهت محاسبه تخمین حالت و کوواریانس استفاده می‌شود

{\hat {\textbf {x}}}_{k\mid k-1}=\sum _{i=0}^{2L}W_{s}^{i}\chi _{k\mid k-1}^{i}

{\textbf {P}}_{k\mid k-1}=\sum _{i=0}^{2L}W_{c}^{i}\ [\chi _{k\mid k-1}^{i}-{\hat {\textbf {x}}}_{k\mid k-1}][\chi _{k\mid k-1}^{i}-{\hat {\textbf {x}}}_{k\mid k-1}]^{\mathrm {T} }

به‌طوری‌که وزن‌های مربوط به حالات و کوواریانس از روابط زیر بدست می‌آیند:

W_{s}^{0}={\frac {\lambda }{L+\lambda }}

W_{c}^{0}={\frac {\lambda }{L+\lambda }}+(1-\alpha ^{2}+\beta )

W_{s}^{i}=W_{c}^{i}={\frac {1}{2(L+\lambda )}}

\lambda =\alpha ^{2}(L+\kappa )-L\,\!

$\alpha$ و $\kappa$ گستردگی نقاط را کنترل می‌کنند. $\beta$ مربوط به توزیع $x$ است.

اگر توزیع $x$ گاوسی باشد، مقادیر طبیعی برابر $\alpha =10^{-3}$ , $\kappa =0$ و $\beta =2$ هستند. $\beta =2$ بهینه است.

آپدیت

پیش‌بینی حالت و کوواریانس مطابق بالا حاصل می‌شوند به جز زمانی که میانگین و کوواریانس نویز مشاهده شده در دست باشد.

{\textbf {x}}_{k\mid k-1}^{a}=[{\hat {\textbf {x}}}_{k\mid k-1}^{\mathrm {T} }\quad E[{\textbf {v}}_{k}^{\mathrm {T} }]\ ]^{\mathrm {T} }

{\textbf {P}}_{k\mid k-1}^{a}={\begin{bmatrix}&{\textbf {P}}_{k\mid k-1}&&0&\\&0&&{\textbf {R}}_{k}&\end{bmatrix}}

مطابق قبل مجموعه‌ای شامل 2L + ۱ نقطه درنظر می‌گیریم

${\begin{aligned}\chi _{k\mid k-1}^{0}&={\textbf {x}}_{k\mid k-1}^{a}\\[6pt]\chi _{k\mid k-1}^{i}&={\textbf {x}}_{k\mid k-1}^{a}+\left({\sqrt {(L+\lambda ){\textbf {P}}_{k\mid k-1}^{a}}}\right)_{i},\qquad i=1,\dots ,L\\[6pt]\chi _{k\mid k-1}^{i}&={\textbf {x}}_{k\mid k-1}^{a}-\left({\sqrt {(L+\lambda ){\textbf {P}}_{k\mid k-1}^{a}}}\right)_{i-L},\qquad i=L+1,\dots ,2L\end{aligned}}$

اگر پیش‌بینی UKF استفاده شده‌باشد، نقاط به صورت زیر مستقلاً قابل محاسبه‌اند.

$\chi _{k\mid k-1}:=[\chi _{k\mid k-1}^{\mathrm {T} }\quad E[{\textbf {v}}_{k}^{\mathrm {T} }]\ ]^{\mathrm {T} }\pm {\sqrt {(L+\lambda ){\textbf {R}}_{k}^{a}}}$

به‌طوری‌که

${\textbf {R}}_{k}^{a}={\begin{bmatrix}&0&&0&\\&0&&{\textbf {R}}_{k}&\end{bmatrix}}$

نقاط به عنوان ورودی تابع h استفاده می‌شوند

$\gamma _{k}^{i}=h(\chi _{k\mid k-1}^{i})\quad i=0..2L$

نقاط وزن‌دار جهت محاسبه مشاهده و کوواریانس مشاهدات پیش‌بینی شده استفاده می‌شوند.

{\hat {\textbf {z}}}_{k}=\sum _{i=0}^{2L}W_{s}^{i}\gamma _{k}^{i}

{\textbf {P}}_{z_{k}z_{k}}=\sum _{i=0}^{2L}W_{c}^{i}\ [\gamma _{k}^{i}-{\hat {\textbf {z}}}_{k}][\gamma _{k}^{i}-{\hat {\textbf {z}}}_{k}]^{\mathrm {T} }

کوواریانس ضربدری حالات و مشاهدات به صورت زیر محاسبه می‌شود

${\textbf {P}}_{x_{k}z_{k}}=\sum _{i=0}^{2L}W_{c}^{i}\ [\chi _{k\mid k-1}^{i}-{\hat {\textbf {x}}}_{k\mid k-1}][\gamma _{k}^{i}-{\hat {\textbf {z}}}_{k}]^{\mathrm {T} }$

که برای محاسبه نتیجه فیلتر کالمن UKF استفاده می‌شود.

$K_{k}={\textbf {P}}_{x_{k}z_{k}}{\textbf {P}}_{z_{k}z_{k}}^{-1}$

همانند فیلتر کالمن، حالت آپدیت شده از جمع حالت پیش‌بینی شده و وزن‌دار کردن نتیجه کالمن محاسبه می‌شود

${\hat {\textbf {x}}}_{k\mid k}={\hat {\textbf {x}}}_{k\mid k-1}+K_{k}({\textbf {z}}_{k}-{\hat {\textbf {z}}}_{k})$

همچنین کوواریانس آپدیت شده برابر است با تفاضل کوواریانس پیش‌بینی شده و کوواریانس محاسبه پیش‌بینی شده که با نتیجه کالمن وزن‌دار شده‌است.

${\textbf {P}}_{k\mid k}={\textbf {P}}_{k\mid k-1}-K_{k}{\textbf {P}}_{z_{k}z_{k}}K_{k}^{\mathrm {T} }$

فیلتر کالمن – بوسی

این فیلتر حالت پیوسته در زمان فیلتر کالمن می‌باشد که نام آن برگرفته از نام ریچارد اسنودن بوسی می‌باشد.

این فیلتر مبتنی بر فضای نمونه حالت مدل شده‌است

{\frac {d}{dt}}\mathbf {x} (t)=\mathbf {F} (t)\mathbf {x} (t)+\mathbf {B} (t)\mathbf {u} (t)+\mathbf {w} (t)

\mathbf {z} (t)=\mathbf {H} (t)\mathbf {x} (t)+\mathbf {v} (t)

به‌طوری‌که $\mathbf {Q} (t)$ و $\mathbf {R} (t)$ قوت نویزهای سفید $\mathbf {w} (t)$ و $\mathbf {v} (t)$ را بیان می‌کند.

فیلتر از دو معادله دیفرانسیلی بدست می‌آید. یکی برای تخمین حالت و دیگری برای کوواریانس.

{\frac {d}{dt}}{\hat {\mathbf {x} }}(t)=\mathbf {F} (t){\hat {\mathbf {x} }}(t)+\mathbf {B} (t)\mathbf {u} (t)+\mathbf {K} (t)(\mathbf {z} (t)-\mathbf {H} (t){\hat {\mathbf {x} }}(t))

{\frac {d}{dt}}\mathbf {P} (t)=\mathbf {F} (t)\mathbf {P} (t)+\mathbf {P} (t)\mathbf {F} ^{T}(t)+\mathbf {Q} (t)-\mathbf {K} (t)\mathbf {R} (t)\mathbf {K} ^{T}(t)

به‌طوری‌که

$\mathbf {K} (t)=\mathbf {P} (t)\mathbf {H} ^{T}(t)\mathbf {R} ^{-1}(t)$

کوواریانس نویز مشاهده‌شده $\mathbf {R} (t)$ معادل کوواریانس خطای پیش‌بینی شده ${\tilde {\mathbf {y} }}(t)=\mathbf {z} (t)-\mathbf {H} (t){\hat {\mathbf {x} }}(t)$ است. این دو کوواریانس تنها در حالت پیوسته زمان برابرند.

تمایز میان حالت پیش‌بینی و آپدیت فیلتر کالمن در اینجا وجود ندارد.

فیلتر کالمن هیبریدی

بسیاری از سیستم‌های فیزیکی به صورت پیوسته در زمان مدل می‌شوند درحالیکه مشاهدات ورودی توسط یک پردازنده دیجیتال و به صورت گسسته در زمان به آن ارائه می‌شوند. به این ترتیب مدل سیستم و مشاهدات به این صورت بیان می‌شود:

${\begin{aligned}{\dot {\mathbf {x} }}(t)&=\mathbf {F} (t)\mathbf {x} (t)+\mathbf {B} (t)\mathbf {u} (t)+\mathbf {w} (t),&\mathbf {w} (t)&\sim N{\bigl (}\mathbf {0} ,\mathbf {Q} (t){\bigr )}\\\mathbf {z} _{k}&=\mathbf {H} _{k}\mathbf {x} _{k}+\mathbf {v} _{k},&\mathbf {v} _{k}&\sim N(\mathbf {0} ,\mathbf {R} _{k})\end{aligned}}$

به‌طوری‌که

$\mathbf {x} _{k}=\mathbf {x} (t_{k})$

مقداردهی

${\hat {\mathbf {x} }}_{0\mid 0}=E{\bigl [}\mathbf {x} (t_{0}){\bigr ]},\mathbf {P} _{0\mid 0}=Var{\bigl [}\mathbf {x} (t_{0}){\bigr ]}$

پیش‌بینی

${\begin{aligned}&{\dot {\hat {\mathbf {x} }}}(t)=\mathbf {F} (t){\hat {\mathbf {x} }}(t)+\mathbf {B} (t)\mathbf {u} (t){\text{, with }}{\hat {\mathbf {x} }}(t_{k-1})={\hat {\mathbf {x} }}_{k-1\mid k-1}\\\Rightarrow &{\hat {\mathbf {x} }}_{k\mid k-1}={\hat {\mathbf {x} }}(t_{k})\\&{\dot {\mathbf {P} }}(t)=\mathbf {F} (t)\mathbf {P} (t)+\mathbf {P} (t)\mathbf {F} (t)^{T}+\mathbf {Q} (t){\text{, with }}\mathbf {P} (t_{k-1})=\mathbf {P} _{k-1\mid k-1}\\\Rightarrow &\mathbf {P} _{k\mid k-1}=\mathbf {P} (t_{k})\end{aligned}}$

این معادلاتت از حالت پیوسته فیلتر کالمن، بدون آپدیت توسط مشاهدات حاصل می‌شوند به‌طوری‌که $\mathbf {K} (t)=0$ . حالت و کوواریانس پیش‌بینی شده با حل مجموعه‌ای از معادلات دیفرانسیلی دارای مقادیر اولیه تخمین حالت قبلی محاسبه می‌شوند.

آپدیت

\mathbf {K} _{k}=\mathbf {P} _{k\mid k-1}\mathbf {H} _{k}^{T}{\bigl (}\mathbf {H} _{k}\mathbf {P} _{k\mid k-1}\mathbf {H} _{k}^{T}+\mathbf {R} _{k}{\bigr )}^{-1}

{\hat {\mathbf {x} }}_{k\mid k}={\hat {\mathbf {x} }}_{k\mid k-1}+\mathbf {K} _{k}(\mathbf {z} _{k}-\mathbf {H} _{k}{\hat {\mathbf {x} }}_{k\mid k-1})

\mathbf {P} _{k\mid k}=(\mathbf {I} -\mathbf {K} _{k}\mathbf {H} _{k})\mathbf {P} _{k\mid k-1}

معادلات آپدیت همان معادلات فیلتر کالمن گسسته هستند.

منبع

در ادامه برای یادگیری بیشتر و آشنایی با کاربردهای فیلتر کالمن پیشنهاد می کنیم فایل های زیر را دانلود و مشاهده فرمایید:

رمز فایل ها : behsanandish.com

kalman Filter

Mobile Robot Localization and Mapping using the Kalman Filter

تئوری تخمین و فیلترهای بهینه

فیلتر کالمن Kalman Filter

محاسبات عددی پیشرفته-فیلتر کالمن

تعریف فیلتر کالمن (Kalman filter) قسمت 1
تعریف فیلتر کالمن (Kalman filter) قسمت 2

آگوست 23, 2019/0 دیدگاه /توسط hgadmin

کدهای متلب،فیلتر گابور

آموزش عمومی پردازش تصویر و بینایی ماشین

فیلتر گابور یک فیلتر خطی است که در کاربردهای مختلفی دارد و در پردازش تصویر مورد استفاده قرار می‌گیرد. به عنوان نمونه، از این فیلتر در لبه‌یابی، استخراج ویژگی و غیره استفاده شده است. بسیاری معتقدند که استخراج ویژگی در گابور مشابه با استخراج ویژگی مغز انسان از تصاویر دریافتی چشم است. به همین خاطر با وجود قدیمی بودن این فیلتر و همچنین کمی زمانبر بودن، هیچ گاه اهمیت خود را از دست نداد و همواره مطالعات و روش‌های زیادی مبتنی بر آن در پردازش تصویر و بینایی ماشین ارایه شده است. فیلتر گابور مبتنی بر دو پارامتر مقیاس و چرخش تعریف می‌شود. با استفاده از مقیاس‌ها و چرخش‌های مختلف تعدادی بانک فیلتر تشکیل می‌شود که از این بانک فیلترها برای استخراج ویژگی در تصویر و یا سایر کاربردها استفاده می‌شود. در تصویر زیر نمونه‌ای از بانک فیلترها در ۵ مقیاس و ۸ چرخش را مشاهده می‌نمایید. با توجه به اینکه ساخت این بانک فیلترها و به دلیل بالا بودن تعداد آن‎‌ها، فیلتر گابور کمی زمانبر محسوب می‌شود، بنابراین کدنویسی بهینه آن بسیار مهم است. در این پست کدهایی از فیلتر گابور را برای شما قرار داده‌ایم که به دلیل عدم استفاده از حلقه‌های for در کدنویسی از سرعت بسیار بالا برخوردار است و همچنین کاملا دقیق پیاده‌سازی شده و می‌توانید با اطمینان از این کدها در پروژه‌های خود بهره ببرید. برای دانلود روی لینک زیر کلیک کنید.

Gabor filter in Matlab

منبع

هم چنین برای دریافت کد های کاملتر همراه با کد GLCM بر روی لینک زیر کلیک کنید:

Gabor filter in matlab with GLCM

تهیه کنندگان: فردین میرزاپور – حسن قاسمیان

رمز فایل : behsanandish.com

آگوست 23, 2019/4 دیدگاه /توسط daliri

تعریف فیلتر کالمن (Kalman filter) قسمت 1

آموزش عمومی پردازش تصویر و بینایی ماشین

فیلتر کالمن (به انگلیسی: Kalman filter) که به عنوان تخمین خطی مرتبه دوم نیز از آن یاد می‌شود، الگوریتمی است که حالت یک سیستم پویا را با استفاده از مجموعه‌ای از اندازه‌گیری‌های شامل خطا در طول زمان برآورد می‌کند. این فیلتر معمولاً تخمین دقیق‌تری را نسبت به تخمین بر مبنای یک اندازه‌گیری واحد را بر مبنای استنباط بیزی و تخمین توزیع احتمال مشترکی از یک متغیر تصادفی در یک مقطع زمانی ارائه می‌کند. این فیلتر از نام رودولف ای کالمن، یکی از پایه‌گذاران این تئوری گرفته شده‌است.

فیلتر کالمن کاربردهای بسیاری در علم و فناوری مانند مسیریابی و پایش وسایل نقلیه، به خصوص هواپیما و فضاپیماها، دارد. فیلتر کالمن مفاهیم گسترده‌ای را در زمینه سری‌های زمانی، پردازش سیگنال و اقتصادسنجی مطرح می‌کند. این فیلتر از مفاهیم پایه در زمینه برنامه‌ریزی و پایش ربات‌ها و همچنین مدلسازی سیستم عصبی محسوب می‌شود. بر اساس تأخیر زمانی میان ارسال فرامین و دریافت پاسخ آن‌ها، استفاده از فیلتر کالمن در تخمین حالات مختلف سیستم را ممکن می‌سازد.

این الگوریتم در دو گام اجرا می‌شود. در گام پیش‌بینی، فیلتر کالمن تخمینی از وضعیت فعلی متغیرها را در شرایط عدم قطعیت ارائه می‌کند. زمانی که نتیجه اندازه‌گیری بعدی بدست آید، تخمین قبلی با میانگین وزن‌دار آپدیت می‌شود. به این ترتیب که وزن اطلاعاتی که دارای قطعیت بیشتری هستند، بیشتر خواهد بود. الگوریتم بازگشتی می‌باشد و با استفاده از ورودی‌های جدید و حالات محاسبه شدهٔ قبلی به‌صورت بی‌درنگ اجرا می‌شود.

درمورد ورودی‌های فیلتر کالمن نمی‌توان بیان کرد که تمام خطاها گوسی هستند. اما در عمل فیلتر برآوردهای احتمالاتی را با فرض توزیع طبیعی داشتن انجام می‌دهد.

مثال کاربردی

تهیه اطلاعات پیوسته و گسسته به روز و دقیق در مورد مکان و سرعت یک شی معین فقط به کمک توالی مشاهدات در مورد موقعیت آن شی، که هر کدام شامل مقداری خطاست امکان‌پذیر است. این فیلتر در طیف گسترده‌ای از کاربری‌های مهندسی از رادار گرفته تا بینایی رایانه‌ای کاربرد دارد. روش فیلتر کالمن یکی از عناوین مهم در تئوری کنترل و مهندسی سیستم‌های کنترلی می‌باشد.

به عنوان مثال، برای کاربری آن در رادار، آنجا که علاقه‌مند به ردیابی هدف هستید، اطلاعات در مورد موقعیت، سرعت و شتاب هدف با حجم عظیمی از انحراف به لطف پارازیت در هر لحظه اندازه‌گیریمی‌شود. فیلتر کالمن از پویایی هدف بهره می‌گیرد به این صورت که سیر تکاملی آن را کنترل می‌کند، تا تأثیرات پارازیت را از بین ببرد و یک برآورد خوب از موقعیت هدف در زمان حال (تصفیه کردن) و در آینده (پیش بینی) یا در گذشته (الحاق یا هموار سازی) ارائه می‌دهد. یک نسخه ساده شده فیلتر کالمن، فیلتر آلفا بتا (alpha beta filter)، که همچنان عموماً استفاده می‌شود از ثابت‌های static weighting به جای ماتریس‌های کواریانس استفاده می‌کند.

نام‌گذاری و تاریخچه توسعه

اگر چه Thorvald Nicolai Thiele و Peter Swerling قبلاً الگوریتم مشابهی ارائه داده بودند، این فیلتر به افتخار Rudolf E. Kalman، فیلتر کالمن نام‌گذاری شد و Stanley F. Schmidt عموماً به خاطر توسعه اولین پیاده‌سازی فیلتر کالمن شهرت یافت. این رخداد هنگام ملاقات با کالمن در مرکز تحقیقاتی ناسا (NASA Ames Research Center) روی داد و وی شاهد کارایی ایده کالمن در برآورد مسیر پرتاب پروژه آپولو بود، که منجر به الحاق آن به رایانه ناوبری آپولو شد. این فیلتر بر روی کاغذ در ۱۹۵۸ توسط Swerling، در ۱۹۶۰ توسط Kalman و در ۱۹۶۱ توسط Kalman and Bucy ایجاد و بسط داده شد.

این فیلتر بعضی مواقع فیلتر Stratonovich-Kalman-Bucy نامیده می‌شود، چرا که یک نمونه خاص از فیلتر بسیار معمولی و غیر خطی ای است که قبلاً توسط Ruslan L. Stratonovich ایجاد شده، در حقیقت معادله این نمونه خاص، فیلتر خطی در اسنادی که از Stratonovich قبل از تابستان ۱۹۶۰، یعنی زمانی که کالمن ،Stratonovich را در کنفرانسی در مسکو ملاقات کرد به چاپ رسید بود.

در تئوری کنترل، فیلتر کالمن بیشتر به برآورد مرتبه دوم (LQE) اشاره دارد. امروزه تنوع گسترده‌ای از فیلتر کالمن بوجود آمده، از فرمول اصلی کالمن در حال حاضر فیلترهای: کالمن ساده، توسعه یافته اشمیت، اطلاعاتی و فیلترهای گوناگون جذر بیرمن، تورنتون و بسیاری دیگر بوجود آمده‌اند. گویا مرسوم‌ترین نوع فیلتر کالمن فاز حلقهٔ بسته (phase-locked loop) می‌باشد که امروزه در رادیوها، رایانه‌ها و تقریباً تمامی انواع ابزارهای تصویری و ارتباطی کاربرد دارد.

اساس مدل سیستم پویا

فیلترهای کالمن بر اساس سیستم‌های خطی پویا (linear dynamical systems) گسسته در بازه زمانی هستند. آن‌ها بر اساس زنجیره مارکوف (Markov chain) به کمک عملگرهای خطی ساخته شده‌اند و توسط نوفه گاوسی (Gaussian noise) تحریک می‌شوند. حالت سیستم توسط برداری از اعداد حقیقی بیان می‌شود. در هر افزایش زمانی که در بازه‌های گسسته صورت می‌گیرد، یک عملگر خطی روی حالت فعلی اعمال می‌شود تا حالت بعدی را با کمی پارازیت ایجاد کند و اختیاراً در صورت شناخت روی کنترل‌کننده‌های سیستم برخی اطلاعات مرتبط را استخراج می‌کند. سپس عملگر خطی دیگر به همراه مقدار دیگری پارازیت خروجی قابل مشاهده‌ای از این حالت نامشخص تولید می‌کند. فیلتر کالمن قادر است مشابه مدل نامشخص مارکوف برخورد کند. با این تفاوت کلیدی که متغییرهای حالت نامشخص در یک فضای پیوسته مقدار می‌گیرند (نقطهٔ مقابل فضای حالت گسسته در مدل مارکوف). بعلاوه، مدل نامشخص مارکوف می‌تواند یک توزیع دلخواه برای مقادیر بعدی متغییرهای حالت ارائه کند، که در تناقض با مدل پارازیت گاوسی‌ای است که در فیلتر کالمن استفاده می‌شود. در اینجا یک دوگانگی بزرگ بین معادلات فیلتر کالمن و آن مدل مارکوف وجود دارد. مقاله‌ای در رابطه با این مدل و دیگر مدل‌ها در Roweis and Ghahramani و فصل ۱۳ Hamilton ارائه شده‌است.

برای تخمین حالت درونی یک فرایند که توسط مجموعه‌ای مشاهدات دارای پارازیت ارائه شده‌است باید آن را منطبق بر چارچوب فیلتر کالمن کنیم. به این منظور ماتریس‌های زیر را ارائه می‌کنیم:

F_{k: مدل انتقال حالات،}

H_{k: مدل مشاهده شده،}

Q_{k: کوواریانس پارازیت فرایند،}

R_{k: کوواریانس پارازیت مشاهده شده،}

B_{k: مدل ورودی-کنترل}

فیلتر کالمن بیان می‌کند که می‌توان حالت k را با استفاده از حالت (k – 1) با استفاده از رابطه زیر محاسبه کرد:

$\mathbf {x} _{k}=\mathbf {F} _{k}\mathbf {x} _{k-1}+\mathbf {B} _{k}\mathbf {u} _{k}+\mathbf {w} _{k}$

به‌طوری‌که:

F_{k: حالت انتقالی اعمال شده به xk−۱،}

B_{k: مدل ورودی-کنترل اعمال شده به بردار کنترلی uk,}

w_{k: فرایند نویزی با توزیع نرمال، میانگین صفر و واریانس Qk}

در زمان k،مشاهده z_k با توجه به حالت x_k به صورت زیر بدست می‌آید:

$\mathbf {z} _{k}=\mathbf {H} _{k}\mathbf {x} _{k}+\mathbf {v} _{k}$

به‌طوری‌که H_k مدل مشاهده شده که به فضای مشاهده شده نگاشت می‌شود و همچنین v_k نویز مشاهده شده با توزیع گاوسی، میانگین صفر و کوواریانس R_k است.

لازم است ذکر شود که حالت اولیه و بردار نویزی در هر محله از هم مستقل هستند.

بسیاری از سیستم‌های پویای واقعی از این مدل تبعیت نمی‌کنند. برخی سیستم‌های پویا حتی در زمانی که منبع ورودی ناشناخته‌ای را بررسی می‌کنیم، می‌توانند موجب کاهش تأثیر این فیلتر شوند. زیرا اثر این سیستم‌ها بر سیگنال ورودی تأثیرگذار است و به این ترتیب می‌تواند موجب ناپایداری تخمین فیلتر شود. به علاوه نویزهای سفید مستقل باعث منشعب شدن فیلتر نمی‌شوند. مسئله تفکیک نویز سفید و سیستم‌های پویا در شاخهٔ نظریه کنترل و در چارچوب کنترل مقاوم بررسی می‌شود.

شرح بیشتر

فیلتر کالمن یک تخمین‌گر بازگشتی است، یعنی تنها تخمین حالت قبل و مشاهده فعلی برای محاسبه تخمین حالت فعلی لازم است. برعکس بسیاری از تخمین‌گرها نیازی به نگهداری اطلاعات تخمین‌ها و مشاهدات تمام حالات قبل نیست. در اینجا ${\hat {\mathbf {x} }}_{n\mid m}$ بیانگر تخمینی از ${\mathbf {x}}$ در زمان n به شرط از مشاهدات پیش از این زمان است.

حالت فعلی فیلتر توسط دو متغیر تشریح می‌شود:

${\hat {\mathbf {x} }}_{k\mid k}$ تخمین حالت پسینی در زمان k به شرط مشاهدات پیش از k.
$\mathbf {P} _{k\mid k}$ ماتریس کوواریانس خطای پسین.

فیلتر کالمن توسط یک معادله بیان می‌شود اما معمولاً آن را به دو بخش پیش‌بینی و آپدیت تفکیک می‌کنند. در گام پیش‌بینی با استفاده از تخمین‌های حالات در بازه‌های زمانی پیشین، تخمینی برای حالت فعلی بدست می‌آید. این تخمین پیش‌بینی شده همان دانش پیشینی است زیرا تنها به تخمین‌های قبلی وابسته است و هیچ مشاهده‌ای در حالت فعلی سیستم را در برنمی‌گیرد. در گام آپدیت تخمین پیشین با مشاهدات فعلی ترکیب می‌شود تا تخمینی از حالت فعلی سیستم ارائه کند.

معمولاً این دو گام متناوباً تکرار می‌شوند، به این معنی که پیش‌بینی تا مشاهده بعدی انجام می‌شود و سپس با استفاده از مشاهدات فعلی آپدیت انجام می‌شود. اگر در بازه زمانی مشاهده‌ای انجام نشود، پیش‌بینی‌ها تا مشاهده بعدی انجام می‌شوند و آپدیت بر مبنای چند مرحله پیش‌بینی انجام می‌شود. به‌طور مشابه اگر در بازه زمانی چندین مشاهده مستقل انجام شود، بر مبنای هریک از آن‌ها چند آپدیت با ماتریس‌های H_k متفاوت بدست می‌آید.

پیش‌بینی

تخمین حالت پیش‌بینی شده (پیشین)	${\hat {\mathbf {x} }}_{k\mid k-1}=\mathbf {F} _{k}{\hat {\mathbf {x} }}_{k-1\mid k-1}+\mathbf {B} _{k}\mathbf {u} _{k}$
تخمین کوواریانس پیش‌بینی شده (پیشین)	$\mathbf {P} _{k\mid k-1}=\mathbf {F} _{k}\mathbf {P} _{k-1\mid k-1}\mathbf {F} _{k}^{\text{T}}+\mathbf {Q} _{k}$

آپدیت

مشاهده جدید وابسته	${\tilde {\mathbf {y} }}_{k}=\mathbf {z} _{k}-\mathbf {H} _{k}{\hat {\mathbf {x} }}_{k\mid k-1}$
کوواریانس جدید وابسته	$\mathbf {S} _{k}=\mathbf {H} _{k}\mathbf {P} _{k\mid k-1}\mathbf {H} _{k}^{T}+\mathbf {R} _{k}$
نتیجه بهینه کالمن	$\mathbf {K} _{k}=\mathbf {P} _{k\mid k-1}\mathbf {H} _{k}^{T}\mathbf {S} _{k}^{-1}$
تخمین حالت آپدیت شده (پسین)	${\hat {\mathbf {x} }}_{k\mid k}={\hat {\mathbf {x} }}_{k\mid k-1}+\mathbf {K} _{k}{\tilde {\mathbf {y} }}_{k}$
تخمین کوواریانس آپدیت شده (پسین)	$\mathbf {P} _{k\|k}=(I-\mathbf {K} _{k}\mathbf {H} _{k})\mathbf {P} _{k\|k-1}$

فرمول کوواریانس آپدیت شده تنها در حالت بهینه بودن فیلتر کالمن کاربرد دارد و در باقی حالات فرمول‌های پیچیده‌تری موردنیاز است که در بخش مشتقات موجود است.

ثابت‌ها

اگر مدلسازی دقیق باشد و ${\hat {\mathbf {x} }}_{0\mid 0}$ و $\mathbf {P} _{0\mid 0}$ بیانگر توزیع حالات ابتدایی سیستم باشند، مقادیر ثابت زیر بدست می‌آیند:

$\operatorname {E} [\mathbf {x} _{k}-{\hat {\mathbf {x} }}_{k\mid k}]=\operatorname {E} [\mathbf {x} _{k}-{\hat {\mathbf {x} }}_{k\mid k-1}]=0$
$\operatorname {E} [{\tilde {\mathbf {y} }}_{k}]=0$

به‌طوری‌که $\operatorname {E} [\xi ]$ امید ریاضی متغیر تصادفی $\xi$ است. در بالا تمامی تخمین‌ها دارای امید ریاضی صفر هستند.

همچنین:

$\mathbf {P} _{k\mid k}=\operatorname {cov} (\mathbf {x} _{k}-{\hat {\mathbf {x} }}_{k\mid k})$ $\mathbf {P} _{k\mid k-1}=\operatorname {cov} (\mathbf {x} _{k}-{\hat {\mathbf {x} }}_{k\mid k-1})$
$\mathbf {S} _{k}=\operatorname {cov} ({\tilde {\mathbf {y} }}_{k})$

به این ترتیب ماتریس‌های کوواریانس نشان‌دهنده مقادیر تخمینی کوواریانس‌ها هستند.

تخمین کوواریانس‌های نویز Q_k و R_k

پیاده‌سازی عملی فیلتر کالمن با توجه به سختی بدست آوردن تخمین ماتریس کوواریانس Q_k و R_k بهینه دشوار است. مطالعات بسیاری جهت بدست آوردن تخمین‌های کوواریانس با توجه به داده‌های موجود انجام شده‌است. یکی از بهترین روش‌ها، تکنیک حداقل مربعات اتوکوواریانس(ALS) است که از اتوکوواریانس داده‌ها با ایجاد تأخیر زمانی برای تخمین استفاده می‌کند. از گنو آکتیو ومتلب جهت محاسبه ماتریس‌های کوواریانس نویز با استفاده از تکنیک حداقل مربعات اتوکوواریانس استفاده می‌شود. این کار به صورت آنلاین توسط پروانه عمومی همگانی گنو امکان‌پذیر است.

بهینگی و کارایی

فیلتر کالمن یک فیلتر خطی بهینه است زیرا الف) مدلسازی آن با دقت بالایی بر سیستم اصلی منطبق است. ب) نویز ورودی، نویز سفید ناهمبسته است. ج) مقدار کوواریانس نویز قابل محاسبه است. روش‌های بسیاری از جمله روش حداقل مربعات اتوکوواریانس که در بالا به آن اشاره شد برای تخمین کوواریانس نویز ارائه شده‌اند. پس از تخمین کوواریانس لازم است کارایی سیستم ارتقا یابد. این بدین معنی است که تخمین حالات سیستم دقیق‌تر شوند. اگر فیلتر کالمن بهینه باشد، نویز ورودی نویز سفید است که محاسبه کارایی سیستم را ممکن می‌سازد. روش‌های زیادی جهت محاسبه کارایی موجود است.

مثال کاربرد عملی

کامیونی دارای اصطکاک در مسیری مستقیم را در نظر بگیرید. کامیون در مکان صفر ثابت است و سپس در مسیری تحت تأثیر نیروهای تصادفی به حرکت در می‌آید. موقعیت کامیون را در هر Δt ثانیه اندازه‌گیری می‌کنیم. اما این اندازه‌گیری مبهم است چرا ما تنها مدلی از مکان و سرعت کامیون را در نظر می‌گیریم. در اینجا فیلتر کالمن را برای این مدل بیان می‌کنیم.

چون $\mathbf {F} ,\mathbf {H} ,\mathbf {R} ,\mathbf {Q}$ ثابت هستند، شاخص‌های زمانی آن‌ها حذف می‌شوند.

موقعیت و سرعت کامیون در فضای خطی موقعیت آن توصیف می‌شود:

$\mathbf {x} _{k}={\begin{bmatrix}x\\{\dot {x}}\end{bmatrix}}$

${\dot {x}}$ سرعت، یعنی مشتق مکان نسبت به زمان است.

فرض کنیم در بازه زمانی میان (k − ۱) و k شتاب a_k که دارای توزیع طبیعی با میانگین صفر و واریانسσ_a است به آن اعمال شود. طبق قوانین حرکت نیوتن داریم:

$\mathbf {x} _{k}=\mathbf {F} \mathbf {x} _{k-1}+\mathbf {G} a_{k}$

$\mathbf {G}$ نتیجه شتابa_k را به سیستم اعمال می‌کند و همچنین داریم

$\mathbf {F} ={\begin{bmatrix}1&\Delta t\\0&1\end{bmatrix}}$

$\mathbf {G} ={\begin{bmatrix}{\frac {\Delta t^{2}}{2}}\\[6pt]\Delta t\end{bmatrix}}$

به این ترتیب

$\mathbf {x} _{k}=\mathbf {F} \mathbf {x} _{k-1}+\mathbf {w} _{k}$

به‌طوری‌که $\mathbf {w} _{k}\sim N(0,\mathbf {Q} )$ و

$\mathbf {Q} =\mathbf {G} \mathbf {G} ^{\text{T}}\sigma _{a}^{2}={\begin{bmatrix}{\frac {\Delta t^{4}}{4}}&{\frac {\Delta t^{3}}{2}}\\[6pt]{\frac {\Delta t^{3}}{2}}&\Delta t^{2}\end{bmatrix}}\sigma _{a}^{2}$

توزیع $N(0,\mathbf {Q} )$ کاملاً پیوسته نیست و بنابراین هیچ تابع توزیع احتمالی ندارد. روش دیگر بیان این توزیع به صورت زیر است:

$\mathbf {w} _{k}\sim \mathbf {G} \cdot N(0,\sigma _{a})$

در هر بازه زمانی، موقعیت کامیون که با نویزی آمیخته‌است در دست است. فرض کنیم این نویز v_k دارای توزیع طبیعی با میانگین صفر و واریانس σ_z باشد،

$\mathbf {z} _{k}=\mathbf {Hx} _{k}+\mathbf {v} _{k}$

به‌طوری‌که

$\mathbf {H} ={\begin{bmatrix}1&0\end{bmatrix}}$

$\mathbf {R} ={\textrm {E}}[\mathbf {v} _{k}\mathbf {v} _{k}^{\text{T}}]={\begin{bmatrix}\sigma _{z}^{2}\end{bmatrix}}$

می‌دانیم موقعیت اولیه کامیون مشخص است و به صورت زیر در نظر گرفته می‌شود

${\hat {\mathbf {x} }}_{0\mid 0}={\begin{bmatrix}0\\0\end{bmatrix}}$

برای اینکه در فیلتر آگاهیمان نسبت به این موضوع را مشخص کنیم، یک ماتریس کوواریانس صفر تعریف می‌کنیم:

$\mathbf {P} _{0\mid 0}={\begin{bmatrix}0&0\\0&0\end{bmatrix}}$

اگر حالت ابتدایی و سرعت به درستی و دقت در دست نباشند، ماتریس کوواریانس باید با توجه به واریانس‌های داده شده و به صورت قطری تعریف شود:

$\mathbf {P} _{0\mid 0}={\begin{bmatrix}\sigma _{x}^{2}&0\\0&\sigma _{\dot {x}}^{2}\end{bmatrix}}$

به این ترتیب فیلتر قادر به محاسبه اطلاعات مدل بر اساس مقادیر اولیه می‌شود.

مشتقات

مشتق‌گیری از ماتریس تخمینی کوواریانس پسین

با توجه به مقدار ثابت کوواریانس خطا P_k | k در بالا

$\mathbf {P} _{k\mid k}=\mathrm {cov} (\mathbf {x} _{k}-{\hat {\mathbf {x} }}_{k\mid k})$

با جایگذاری ${\hat {\mathbf {x} }}_{k\mid k}$ از روابط اثبات شده خواهیم داشت

$\mathbf {P} _{k\mid k}={\textrm {cov}}(\mathbf {x} _{k}-({\hat {\mathbf {x} }}_{k\mid k-1}+\mathbf {K} _{k}{\tilde {\mathbf {y} }}_{k}))$

حال مقدار ${\tilde {\mathbf {y} }}_{k}$ را جایگزین می‌کنیم

$\mathbf {P} _{k\mid k}={\textrm {cov}}(\mathbf {x} _{k}-({\hat {\mathbf {x} }}_{k\mid k-1}+\mathbf {K} _{k}(\mathbf {z} _{k}-\mathbf {H} _{k}{\hat {\mathbf {x} }}_{k\mid k-1})))$

همچنین $\mathbf {z} _{k}$ را نیز در رابطه جایگذاری می‌کنیم

$\mathbf {P} _{k\mid k}={\textrm {cov}}(\mathbf {x} _{k}-({\hat {\mathbf {x} }}_{k\mid k-1}+\mathbf {K} _{k}(\mathbf {H} _{k}\mathbf {x} _{k}+\mathbf {v} _{k}-\mathbf {H} _{k}{\hat {\mathbf {x} }}_{k\mid k-1})))$

با توجه به بردار خطا

$\mathbf {P} _{k|k}={\textrm {cov}}((I-\mathbf {K} _{k}\mathbf {H} _{k})(\mathbf {x} _{k}-{\hat {\mathbf {x} }}_{k\mid k-1})-\mathbf {K} _{k}\mathbf {v} _{k})$

چون خطای اندازه‌گیری شدهv_k نسبت به سایر متغیرها ناهمبسته است، می‌توان گفت

$\mathbf {P} _{k|k}={\textrm {cov}}((I-\mathbf {K} _{k}\mathbf {H} _{k})(\mathbf {x} _{k}-{\hat {\mathbf {x} }}_{k\mid k-1}))+{\textrm {cov}}(\mathbf {K} _{k}\mathbf {v} _{k})$

با توجه به ویژگی‌های ماتریس کوواریانس

$\mathbf {P} _{k\mid k}=(I-\mathbf {K} _{k}\mathbf {H} _{k}){\textrm {cov}}(\mathbf {x} _{k}-{\hat {\mathbf {x} }}_{k\mid k-1})(I-\mathbf {K} _{k}\mathbf {H} _{k})^{\text{T}}+\mathbf {K} _{k}{\textrm {cov}}(\mathbf {v} _{k})\mathbf {K} _{k}^{\text{T}}$

با توجه به ثابت بودن P_k | k−1 و تعریف R_k نتیجه می‌شود

$\mathbf {P} _{k\mid k}=(I-\mathbf {K} _{k}\mathbf {H} _{k})\mathbf {P} _{k\mid k-1}(I-\mathbf {K} _{k}\mathbf {H} _{k})^{\text{T}}+\mathbf {K} _{k}\mathbf {R} _{k}\mathbf {K} _{k}^{\text{T}}$

این فرمول برای هر مقدار K_k معتبر است. فرمول بالا بیان می‌کند اگر K_k نتیجه بهینه کالمن باشد، رابطه به شکل زیر ساده خواهد شد.

مشتق نتیجه کالمن

فیلتر کالمن یک تخمین‌گر کمینه مربع میانگین خطا (MMSE) است. خطا در تخمین حالت پسین برابر است با

$\mathbf {x} _{k}-{\hat {\mathbf {x} }}_{k\mid k}$

هدف ما کمینه کردن میانگین مربع این بردار خطا یعنی ${\textrm {E}}[\|\mathbf {x} _{k}-{\hat {\mathbf {x} }}_{k|k}\|^{2}]$ است. این معادل کمینه کردن اثر تخمین پسین ماتریس کوواریانس $\mathbf {P} _{k|k}$ است. با بسط رابطه بالا نتیجه می‌شود:

${\begin{aligned}\mathbf {P} _{k\mid k}&=\mathbf {P} _{k\mid k-1}-\mathbf {K} _{k}\mathbf {H} _{k}\mathbf {P} _{k\mid k-1}-\mathbf {P} _{k\mid k-1}\mathbf {H} _{k}^{\text{T}}\mathbf {K} _{k}^{\text{T}}+\mathbf {K} _{k}(\mathbf {H} _{k}\mathbf {P} _{k\mid k-1}\mathbf {H} _{k}^{\text{T}}+\mathbf {R} _{k})\mathbf {K} _{k}^{\text{T}}\\[6pt]&=\mathbf {P} _{k\mid k-1}-\mathbf {K} _{k}\mathbf {H} _{k}\mathbf {P} _{k\mid k-1}-\mathbf {P} _{k\mid k-1}\mathbf {H} _{k}^{\text{T}}\mathbf {K} _{k}^{\text{T}}+\mathbf {K} _{k}\mathbf {S} _{k}\mathbf {K} _{k}^{\text{T}}\end{aligned}}$

اثر ماتریس زمانی کمینه می‌شود که حساب ماتریس صفر شود. با استفاده از خواص ماتریس گرادیان و تقارن ماتریس‌ها داریم:

${\frac {\partial \;\mathrm {tr} (\mathbf {P} _{k\mid k})}{\partial \;\mathbf {K} _{k}}}=-2(\mathbf {H} _{k}\mathbf {P} _{k\mid k-1})^{\text{T}}+2\mathbf {K} _{k}\mathbf {S} _{k}=0$

اگر این معادله را برای K_k حل کنیم، نتیجه کالمن بدست می‌آید

$\mathbf {K} _{k}\mathbf {S} _{k}=(\mathbf {H} _{k}\mathbf {P} _{k\mid k-1})^{\text{T}}=\mathbf {P} _{k\mid k-1}\mathbf {H} _{k}^{\text{T}}$

$\mathbf {K} _{k}=\mathbf {P} _{k\mid k-1}\mathbf {H} _{k}^{\text{T}}\mathbf {S} _{k}^{-1}$

این عبارت همان نتیجه بهینه کالمن است.

ساده کردن فرمول کوواریانس خطای پسین

با استفاده از نتیجه بهینه کالمن که در بالا بدست آمد می‌توان فرمول کوواریانس خطای پسین را ساده‌تر کرد. اگر طرفیت رابطه نتیجه بهینه کالمن را در S_kK_k^T ضرب کنیم، داریم:

$\mathbf {K} _{k}\mathbf {S} _{k}\mathbf {K} _{k}^{\mathrm {T} }=\mathbf {P} _{k\mid k-1}\mathbf {H} _{k}^{\mathrm {T} }\mathbf {K} _{k}^{\mathrm {T} }$

با استفاده از فرمول بسط داده شده کوواریانس خطای پسین

$\mathbf {P} _{k\mid k}=\mathbf {P} _{k\mid k-1}-\mathbf {K} _{k}\mathbf {H} _{k}\mathbf {P} _{k\mid k-1}-\mathbf {P} _{k\mid k-1}\mathbf {H} _{k}^{\mathrm {T} }\mathbf {K} _{k}^{\mathrm {T} }+\mathbf {K} _{k}\mathbf {S} _{k}\mathbf {K} _{k}^{\mathrm {T} }$

با ساده‌سازی دو جملهٔ آخر نتیجه می‌شود

$\mathbf {P} _{k\mid k}=\mathbf {P} _{k\mid k-1}-\mathbf {K} _{k}\mathbf {H} _{k}\mathbf {P} _{k\mid k-1}=(I-\mathbf {K} _{k}\mathbf {H} _{k})\mathbf {P} _{k\mid k-1}$

این فرمول در محاسبه بسیار راحت‌تر است اما تنها برای نتیجه بهینه کاربرد دارد و زمانی که نتیجه کالمن بهینه نباشد باید از همان فرمول قبلی استفاده کرد.

تحلیل درستی

معادلات فیلتر کردن کالمن تخمینی بازگشتی برای حالت ${\hat {\mathbf {x} }}_{k\mid k}$ و کوواریانس خطای $\mathbf {P} _{k\mid k}$ ارائه می‌کند. دقت تخمین به پارامترهای سیستم و نویز ورودی تخمین‌گر بستگی دارد. در غیاب مقادیر ماتریس‌های کوواریانس $\mathbf {Q} _{k}$ و $\mathbf {R} _{k}$ عبارت

$\mathbf {P} _{k\mid k}=(\mathbf {I} -\mathbf {K} _{k}\mathbf {H} _{k})\mathbf {P} _{k\mid k-1}(\mathbf {I} -\mathbf {K} _{k}\mathbf {H} _{k})^{\mathrm {T} }+\mathbf {K} _{k}\mathbf {R} _{k}\mathbf {K} _{k}^{\mathrm {T} }$

مقدار درست کوواریانس خطا را ارائه نمی‌کند. به عبارت دیگر، $\mathbf {P} _{k\mid k}\neq E[(\mathbf {x} _{k}-{\hat {\mathbf {x} }}_{k\mid k})(\mathbf {x} _{k}-{\hat {\mathbf {x} }}_{k\mid k})^{\mathrm {T} }]$ . در بسیاری از کاربردهای بی‌درنگ، ماتریس‌های کوواریانس مورد استفاده در طراحی فیلتر کالمن با مقادیر واقعی ماتریس‌های کوواریانس تفاوت دارند. این تحلیل بیان می‌دارد که تخمین کوواریانس خطا زمانی که ماتریس‌های ورودی سیستم $\mathbf {F} _{k}$ و $\mathbf {H} _{k}$ باشند، نادرست است.

این بحث به حالتی که عدم قطعیت درمورد خطا داریم محدود می‌شود. حال مقادیر واقعی کوواریانس نویز را $\mathbf {Q} _{k}^{a}$ و $\mathbf {R} _{k}^{a}$ تعریف می‌کنیم به‌طوری‌که مقادیر آن‌ها به ترتیب در روابط جایگزین $\mathbf {Q} _{k}$ و $\mathbf {R} _{k}$ شوند. مقدار واقعی کوواریانس خطا را $\mathbf {P} _{k\mid k}^{a}$ و $\mathbf {P} _{k\mid k}$ با فیلتر کالمن محاسبه می‌شوند. اگر $\mathbf {Q} _{k}\equiv \mathbf {Q} _{k}^{a}$ و $\mathbf {R} _{k}\equiv \mathbf {R} _{k}^{a}$ $\mathbf {P} _{k\mid k}=\mathbf {P} _{k\mid k}^{a}$ خواهد بود. با محاسبه مقدار واقعی کوواریانس خطا $\mathbf {P} _{k\mid k}^{a}=E[(\mathbf {x} _{k}-{\hat {\mathbf {x} }}_{k\mid k})(\mathbf {x} _{k}-{\hat {\mathbf {x} }}_{k\mid k})^{\mathrm {T} }]$ و جایگذاری ${\widehat {\mathbf {x} }}_{k\mid k}$ و در نظر داشتن اینکه $E[\mathbf {w} _{k}\mathbf {w} _{k}^{\mathrm {T} }]=\mathbf {Q} _{k}^{a}$ and $E[\mathbf {v} _{k}\mathbf {v} _{k}^{\mathrm {T} }]=\mathbf {R} _{k}^{a}$ معادلات بازگشتی برای $\mathbf {P} _{k\mid k}^{a}$ بدست می‌آید:

$\mathbf {P} _{k\mid k-1}^{a}=\mathbf {F} _{k}\mathbf {P} _{k-1\mid k-1}^{a}\mathbf {F} _{k}^{\mathrm {T} }+\mathbf {Q} _{k}^{a}$

$\mathbf {P} _{k\mid k}^{a}=(\mathbf {I} -\mathbf {K} _{k}\mathbf {H} _{k})\mathbf {P} _{k\mid k-1}^{a}(\mathbf {I} -\mathbf {K} _{k}\mathbf {H} _{k})^{\mathrm {T} }+\mathbf {K} _{k}\mathbf {R} _{k}^{a}\mathbf {K} _{k}^{\mathrm {T} }$

محاسبه $\mathbf {P} _{k\mid k}$ با فرض $E[\mathbf {w} _{k}\mathbf {w} _{k}^{\mathrm {T} }]=\mathbf {Q} _{k}$ و $E[\mathbf {v} _{k}\mathbf {v} _{k}^{\mathrm {T} }]=\mathbf {R} _{k}$ انجام می‌شود. روابط بازگشتی برای $\mathbf {P} _{k\mid k}^{a}$ و $\mathbf {P} _{k\mid k}$ جز زمانی که $\mathbf {Q} _{k}^{a}$ و $\mathbf {R} _{k}^{a}$ را به ترتیب به جای $\mathbf {Q} _{k}$ و $\mathbf {R} _{k}$ در نظر بگیریم، یکتا هستند.

ریشه مربع

یکی از مشکلات فیلتر کالمن ثبات عددی است. اگر کوواریانس نویز Q_k کوچک باشد، مقدار ویژه آن منفی می‌شود. به این ترتیب ماتریس کوواریانس حالات P نامعین می‌شود در حالیکه باید مثبت معین باشد.

یک ویژگی ماتریس‌های مثبت معین این است که ریشه مربعی ماتریس مثلثی P = S·S^T دارند. این ریشه می‌تواند به کمک روش تفکیک چولسکی (Cholesky decomposition) محاسبه شود. اگر کوواریانس به این فرم نوشته شود، هیچ‌گاه قطری یا متقارن نخواهد بود. یک فرم معادل این ماتریس که با استفاده از تفکیک U-D بدست می‌آید، P = U·D·U^T

است کهU یک ماتریس مثلثی واحد و D یک ماتریس قطری است. در میان این دو فرم، فرم U-D رایج‌تر است و نیاز به محاسبات کمتری دارد.

الگوریتم‌های کارای پیش‌بینی و آپدیت کالمن در فرم ریشه مربعی، توسط بیرمن و تورتون ارائه شدند.

‘تفکیک’L·D·L^T ماتریس کوواریانسS_k مبنای دیگر فیلترهای عددی و ریشه مربعی است. الگوریتم با تفکیک LU آغاز می‌شود و نتایج آن در ساختارL·D·L^T وارد می‌شود تا به روش Golub و Van Loan (الگوریتم ۴٫۱٫۲) در ماتریس قطری غیر واحد انجام شود.

ارتباط با تخمین بازگشتی بیز

فیلتر کالمن یکی از ساده‌ترین شبکه‌های پویای بیزی است. فیلتر کالمن حالات فعلی سیستم را در طول زمان به صورت بازگشتی، با استفاده از اندازه‌گیری‌های ورودی در مدل فرایندی ریاضی تخمین می‌زند. به‌طور مشابه تخمین بازگشتی بیز، توابع توزیع احتمال ناشناخته را به صورت بازگشتی، با استفاده از اندازه‌گیری‌های ورودی در مدل فرایندی ریاضی در طول زمان تخمین می‌زند.^[۲۰]

در تخمین بازگشتی بیز، حالت فعلی یک فرایند مارکوف مشاهده نشده در نظر گرفته می‌شود و اندازه‌گیری‌های مشاهده شده مدل پنهان مارکف (HMM) هستند.

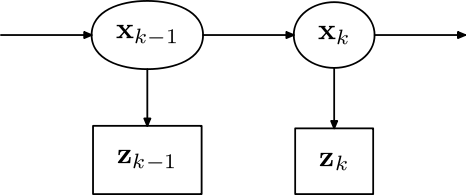
با فرض مارکوف، حالت فعلی سیستم مستقل از تمام حالات پیش از حالت قبلی آن است.

$p({\textbf {x}}_{k}\mid {\textbf {x}}_{0},\dots ,{\textbf {x}}_{k-1})=p({\textbf {x}}_{k}\mid {\textbf {x}}_{k-1})$

به‌طور مشابه اندازه‌گیری در بازه زمانی kام تنها به حالت قبلی وابسته است و مستقل از تمام حالات پیش از حالت قبلی آن است.

$p({\textbf {z}}_{k}\mid {\textbf {x}}_{0},\dots ,{\textbf {x}}_{k})=p({\textbf {z}}_{k}\mid {\textbf {x}}_{k})$

با این مفروضات، توزیع احتمال تمام حالات مدل پنهان مارکوف به صورت زیر بیان می‌شود:

$p({\textbf {x}}_{0},\dots ,{\textbf {x}}_{k},{\textbf {z}}_{1},\dots ,{\textbf {z}}_{k})=p({\textbf {x}}_{0})\prod _{i=1}^{k}p({\textbf {z}}_{i}\mid {\textbf {x}}_{i})p({\textbf {x}}_{i}\mid {\textbf {x}}_{i-1})$

هدف فیلتر کالمن تخمین حالت فعلی سیستم است. این تخمین با استفاده از حاشیه‌سازی تابع توزیع مشترک بر اساس حالت قبلی سیستم قابل محاسبه است. کافی است حاشیه‌سازی نسبت به تمام حالات قبل انجام شده و بر احتمال مجموعه اندازه‌گیری‌ها تقسیم شود.

به این ترتیب گام‌های پیش‌بینی و آپدیت فیلتر کالمن به صورت احتمالاتی بدست می‌آیند. توزیع احتمال حالت پیش‌بینی شده حاصل انتگرال حاصلضرب توابع توزیع احتمال انتقال از حالت (k-1)ام به حالت kام است و حالت قبلی روی تمام $x_{k-1}$ های ممکن است.

$p({\textbf {x}}_{k}\mid {\textbf {Z}}_{k-1})=\int p({\textbf {x}}_{k}\mid {\textbf {x}}_{k-1})p({\textbf {x}}_{k-1}\mid {\textbf {Z}}_{k-1})\,d{\textbf {x}}_{k-1}$

اندازه‌گیری‌ها تا بازه زمانی kام عبارتند از:

${\textbf {Z}}_{t}=\left\{{\textbf {z}}_{1},\dots ,{\textbf {z}}_{t}\right\}$

توزیع احتمال آپدیت از حاصلضرب پیش‌بینی و احتمال بخت (likelihood) بدست می‌آید.

$p({\textbf {x}}_{k}\mid {\textbf {Z}}_{k})={\frac {p({\textbf {z}}_{k}\mid {\textbf {x}}_{k})p({\textbf {x}}_{k}\mid {\textbf {Z}}_{k-1})}{p({\textbf {z}}_{k}\mid {\textbf {Z}}_{k-1})}}$

به‌طوری‌که

$p({\textbf {z}}_{k}\mid {\textbf {Z}}_{k-1})=\int p({\textbf {z}}_{k}\mid {\textbf {x}}_{k})p({\textbf {x}}_{k}\mid {\textbf {Z}}_{k-1})\,d{\textbf {x}}_{k}$

ضریب نرمال‌سازی است.

توابع توزیع احتمال باقی‌مانده عبارتند از:

$p({\textbf {x}}_{k}\mid {\textbf {x}}_{k-1})={\mathcal {N}}({\textbf {F}}_{k}{\textbf {x}}_{k-1},{\textbf {Q}}_{k})$

$p({\textbf {z}}_{k}\mid {\textbf {x}}_{k})={\mathcal {N}}({\textbf {H}}_{k}{\textbf {x}}_{k},{\textbf {R}}_{k})$

$p({\textbf {x}}_{k-1}\mid {\textbf {Z}}_{k-1})={\mathcal {N}}({\hat {\textbf {x}}}_{k-1},{\textbf {P}}_{k-1})$

توجه کنید که تابع چگالی احتمال حالت قبل، یک تخمین است. فیلتر کالمن فیلتری بهینه است و به این ترتیب توزیع احتمال $\mathbf {x} _{k}$ به شرط اندازه‌گیری $\mathbf {Z} _{k}$ یک تخمین بهینه توسط فیلتر کالمن است.

تعریف فیلتر کالمن (Kalman filter) قسمت 1
تعریف فیلتر کالمن (Kalman filter) قسمت 2

مارس 9, 2019/0 دیدگاه /توسط daliri

فصل اول: توابع اولیه متلب

آموزش پردازش تصویر در نرم افزار متلب (Matlab)

مقدمه

آموزش توابع اولیه پردازش تصویر در متلب (فصل اول) : در این مجموعه قصد داریم به آموزش فهرست وار و سریع «جعبه ابزار پردازش تصویر» در نرم افزار متلب (Matlab) بپردازیم. سعی ما بر این است تا در پروژه های رایگانی که در سایت قرار می دهیم با لینک هر دستور به صفحه آموزشی آن، بتوانیم خیلی سریع و آسان با کاربرد دستورات و توابع مورد استفاده آشنا بشویم. در این مجموعه آموزشی فرض ما بر این است که دوستان آشنایی نسبی با نرم افزار متلب دارند و فعلا وارد این حوزه نمی شویم.

«فصل اول: آموزش توابع اولیه پردازش تصویر در متلب»

تابع ()imread :

هدف : هدف از این تابع خواندن تصویر از فایل می باشد.

نحوه استفاده :

imread( مسیر فایل )

مثال :

img= imread('c:\1.jpg');

تابع ()imshow :

هدف : هدف از این تابع نمایش تصویر می باشد.

نحوه استفاده :

imshow(نام متغیر)

مثال :

img= imread('c:\1.jpg');
imshow(img)

خروجی دستور :

تابع ()subplot:

هدف : جهت نمایش تصاویر بطور همزمان و در یک پنجره.

نحوه استفاده :


subplot( rows , columns , image number) , imshow( pic )

مثال :


subplot(131);
imshow(img(:,:,1)); 

subplot(132);
imshow(img(:,:,2)); 

subplot(133);
imshow(img(:,:,3));

خروجی دستور:

تابع ()title:

هدف : جهت نمایش توضیحات در مورد آخرین تصویر نمایش داده شده.

نحوه استفاده :

imshow(img); 
title('Red')

مثال :

subplot(131); 
imshow(img(:,:,1)); 
title('Red'); 

subplot(132); 
imshow(img(:,:,2)); 
title('Green'); 

subplot(133); 
imshow(img(:,:,3)); 
title('Blue'); ;

خروجی دستور :

تابع ()figure :

هدف : جهت نمایش تصویر در پنجره های جداگانه. در صورتی که بخواهیم خروجی دستور imshow در پنجره ای جدید باز شود از این دستور استفاده می شود.

نحوه استفاده :

figure , imshow( pic )

مثال :

figure , imshow( pic )

تابع ()imwrite :

هدف : هدف از این تابع ذخیره تصویر بصورت فایل می باشد.

نحوه استفاده :

imwrite( pic , path)

مثال :

 imwrite( pic , 'c:\1.jpg');

تابع ()iminfo:

هدف : نمایش اطلاعات تصویر.

نحوه استفاده :

iminfo( pic )

مثال :

 iminfo( peppers.png);

خروجی دستور:


ans =

 Filename: '/Applications/MATLAB_R2014a.app/toolbox/matla...'
FileModDate: '02-Apr-2013 15:55:52'
FileSize: 287677
Format: 'png'
FormatVersion: []
Width: 512
Height: 384
BitDepth: 24
ColorType: 'truecolor'
FormatSignature: [137 80 78 71 13 10 26 10]
Colormap: []
Histogram: []
InterlaceType: 'none'
Transparency: 'none'
SimpleTransparencyData: []
BackgroundColor: []
RenderingIntent: []
Chromaticities: []
Gamma: []
XResolution: []
YResolution: []
ResolutionUnit: []
XOffset: []
YOffset: []
OffsetUnit: []
SignificantBits: []
ImageModTime: '16 Jul 2002 16:46:41 +0000'
Title: []
Author: []
Description: 'Zesty peppers'
Copyright: 'Copyright The MathWorks, Inc.'
CreationTime: []
Software: []
Disclaimer: []
Warning: []
Source: []
Comment: []
OtherText: []

تابع ()imtool:

هدف : نمایش اطلاعات تصویر.

علاوه بر نمایش تصویر در دو پنجره دیگر امکاناتی جهت مشاهده کد رنگ یک پیکسل و خط کش وجود دارد.

نحوه استفاده :

imtool( pic )

مثال :

 imtool( coins.png);

خروجی دستور:

پایان آموزش پردازش تصویر در متلب (فصل اول)

ژانویه 22, 2018/0 دیدگاه /توسط admin

بایگانی برچسب برای: کنترل تردد

برآورد پارامترهای رگرسیون خطی ساده

مثال

مفهوم رگرسیون

تاریخچه رگرسیون

مدل رگرسیون خطی ساده

تنظیم مدل (Regularization)

تفسیر احتمالی تنظیم مدل

تخمین پارامترها برای مسائل چند متغیره

صورت مسئله

تخمین پارامتر بهینه از روش کمترین مربعات

تخمین پارامتر بهینه از روش گرادیان کاهشی تصادفی (Stochastic Gradient Descent)

تفسیر احتمالی از طریق درست نمایی بیشینه

تخمین پارامترها برای مسائل تک متغیره

تفاوت رگرسیون و همبستگی بر اساس هدف:

تفاوت رگرسیون و همبستگی براساس روش:

بخت حاشیه‌ای

فیلتر اطلاعاتی

تصفیه‌کننده تأخیر زمانی

تصفیه‌کننده بازه

Rauch–Tung–Striebel

تصفیه‌کننده Bryson–Frazier

تصفیه‌کننده کمینه واریانس

فیلترهای وزن‌دار کالمن

فیلترهای غیرخطی

فیلتر کالمن بسط‌یافته – EKF

فیلتر کالمن از نوع UKF – Unscented

پیش‌بینی

آپدیت

فیلتر کالمن – بوسی

فیلتر کالمن هیبریدی

مقداردهی

پیش‌بینی

هم چنین برای دریافت کد های کاملتر همراه با کد GLCM بر روی لینک زیر کلیک کنید:

مثال کاربردی

نام‌گذاری و تاریخچه توسعه

اساس مدل سیستم پویا

شرح بیشتر

پیش‌بینی

آپدیت

ثابت‌ها

تخمین کوواریانس‌های نویز Qk و Rk

بهینگی و کارایی

مثال کاربرد عملی

مشتقات

مشتق‌گیری از ماتریس تخمینی کوواریانس پسین

مشتق نتیجه کالمن

ساده کردن فرمول کوواریانس خطای پسین

تحلیل درستی

ریشه مربع

ارتباط با تخمین بازگشتی بیز

مقدمه

«فصل اول: آموزش توابع اولیه پردازش تصویر در متلب»

تابع ()imread :

تابع ()imshow :

تابع ()subplot:

تابع ()title:

تابع ()figure :

تابع ()imwrite :

تابع ()iminfo:

تابع ()imtool:

پایان آموزش پردازش تصویر در متلب (فصل اول)

تلفن های تماس:

ساعات کاری

پیوند ها :

محصولات :

تخمین کوواریانس‌های نویز Q_k و R_k