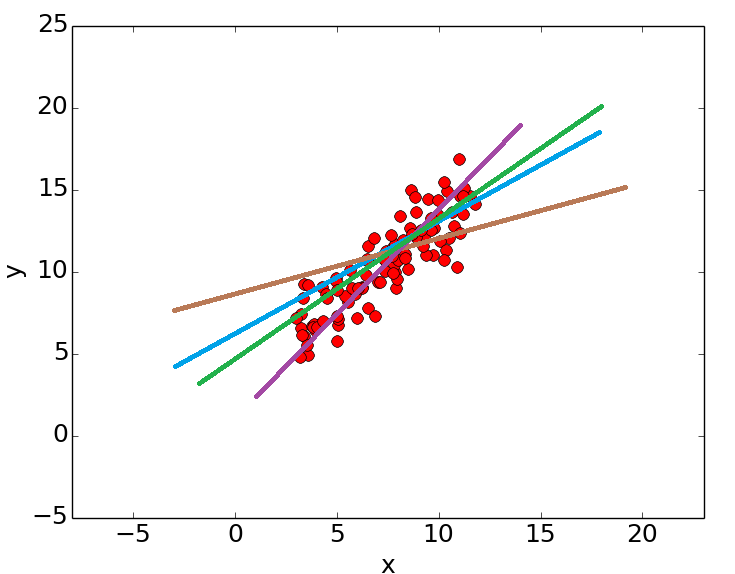
داده ها در اعماق زندگی روزانه ما ریشه دوانده اند، از خرید روزانه تا انتخاب مدرسه و پزشک و مسافرت های ما امروزه داده محور شده اند. این امر نیاز به الگوریتم ها وروشهای هوشمند پردازش داده و یادگیری ماشین را صد چندان کرده است .در این آموزش، بیشتر بر مفاهیم اصلی و الگوریتم ها تاکید شده است و مفاهیم ریاضی و آماری را باید از سایر منابع فرابگیرید .
انواع الگوریتم های یادگیری ماشین
سه نوع اصلی الگوریتم های یادگیری ماشین از قرار زیرند :
- یادگیری نظارت شده (هدایت شده – Supervised Learning) : در این نوع از الگوریتم ها که بار اصلی یادگیری ماشین را بر دوش می کشند (از لحاظ تعداد الگوریتم های این نوع)، با دو نوع از متغیرها سروکار داریم . نوع اول که متغیرهای مستقل نامیده میشوند، یک یا چند متغیر هستند که قرار است بر اساس مقادیر آنها، یک متغیر دیگر را پیش بینی کنیم. مثلا سن مشتری و تحصیلات و میزان درآمد و وضعیت تاهل برای پیش بینی خرید یک کالا توسط یک مشتری ، متغیرهای مستقل هستند. نوع دوم هم متغیرهای وابسته یا هدف یا خروجی هستند و قرار است مقادیر آنها را به کمک این الگوریتم ها پیش بینی کنیم . برای این منظور باید تابعی ایجاد کنیم که ورودیها (متغیرهای مستقل) را گرفته و خروجی موردنظر (متغیر وابسته یا هدف) را تولید کند. فرآیند یافتن این تابع که در حقیقت کشف رابطه ای بین متغیرهای مستقل و متغیرهای وابسته است را فرآیند آموزش (Training Process) می گوئیم که روی داده های موجود (داده هایی که هم متغیرهای مستقل و هم متغیرهای وابسته آنها معلوم هستند مثلا خریدهای گذشته مشتریان یک فروشگاه) اعمال میشود و تا رسیدن به دقت لازم ادامه می یابد. نمونه هایی از این الگوریتم ها عبارتند از رگرسیون، درختهای تصمیم ، جنگل های تصادفی، N نزدیک ترین همسایه، و رگرسیون لجستیک می باشند.
- یادگیری بدون ناظر (unsupervised learning) : در این نوع از الگوریتم ها ، متغیر هدف نداریم و خروجی الگوریتم، نامشخص است. بهترین مثالی که برای این نوع از الگوریتم ها می توان زد، گروه بندی خودکار (خوشه بندی) یک جمعیت است مثلاً با داشتن اطلاعات شخصی و خریدهای مشتریان، به صورت خودکار آنها را به گروه های همسان و هم ارز تقسیم کنیم . الگوریتم Apriori و K-Means از این دسته هستند.

- یادگیری تقویت شونده (Reinforcement Learning) : نوع سوم از الگوریتم ها که شاید بتوان آنها را در زمره الگوریتم های بدون ناظر هم دسته بندی کرد، دسته ای هستند که از آنها با نام یادگیری تقویت شونده یاد میشود. در این نوع از الگوریتم ها، یک ماشین (در حقیقت برنامه کنترل کننده آن)، برای گرفتن یک تصمیم خاص ، آموزش داده می شود و ماشین بر اساس موقعیت فعلی (مجموعه متغیرهای موجود) و اکشن های مجاز (مثلا حرکت به جلو ، حرکت به عقب و …) ، یک تصمیم را می گیرد که در دفعات اول، این تصمیم می تواند کاملاً تصادفی باشد و به ازای هر اکشن یا رفتاری که بروز می دهد، سیستم یک فیدبک یا بازخورد یا امتیاز به او میدهد و از روی این فیدبک، ماشین متوجه میشود که تصمیم درست را اتخاذ کرده است یا نه که در دفعات بعد در آن موقعیت ، همان اکشن را تکرار کند یا اکشن و رفتار دیگری را امتحان کند. با توجه به وابسته بودن حالت و رفتار فعلی به حالات و رفتارهای قبلی، فرآیند تصمیم گیری مارکوف ، یکی از مثالهای این گروه از الگوریتم ها می تواند باشد . الگوریتم های شبکه های عصبی هم می توانند ازین دسته به حساب آیند. منظور از کلمه تقویت شونده در نام گذاری این الگوریتم ها هم اشاره به مرحله فیدبک و بازخورد است که باعث تقویت و بهبود عملکرد برنامه و الگوریتم می شود .
نمونه ای از دسته بندی کلاسیک الگوریتم های یادگیری ماشین که بر اساس وجود یا عدم وجود عامل کنترل کننده (ناظر) و گسسته و پیوسته بودن متغیرها انجام شده است را می توانید در این شکل ببینید :
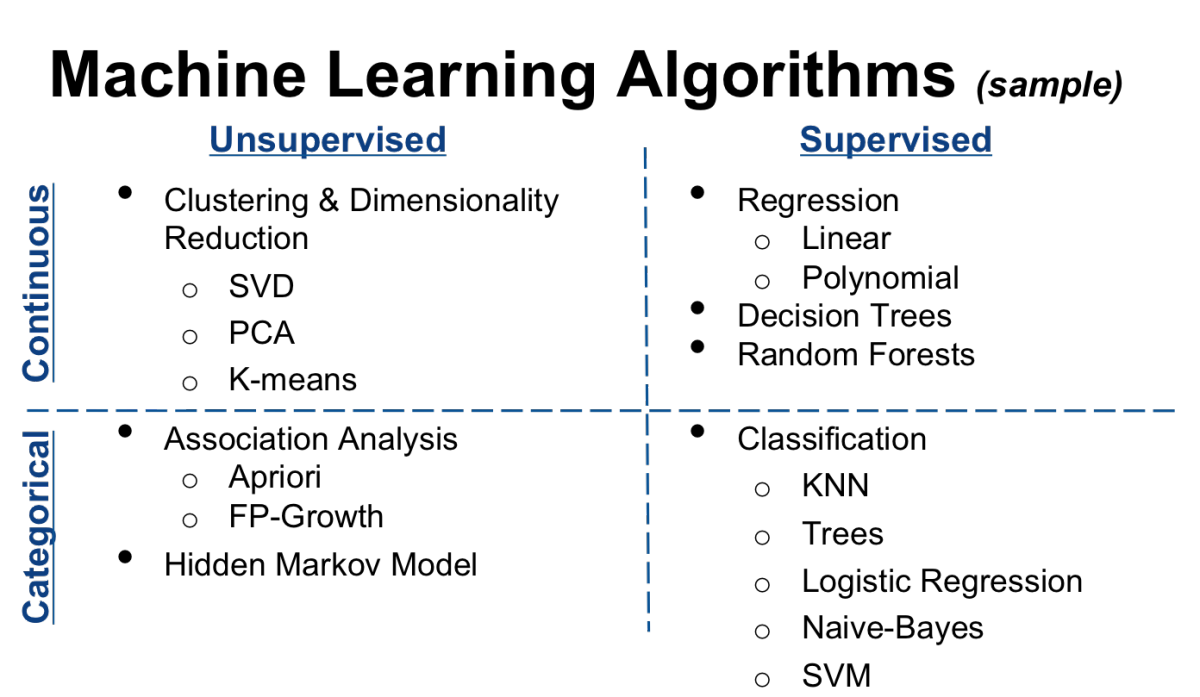
الگوریتم های اصلی و رایج یادگیری ماشین
در این سری از مقالات به آموزش الگوریتم های زیر با نمونه کدهای لازم و مثالهای تشریحی، خواهیم پرداخت :
- رگرسیون خطی
- رگرسیون لجستیک
- درخت تصمیم
- SVM
- Naive Bayes
- KNN
- K-Means
- جنگل تصادفی
- الگوریتم های کاهش ابعاد
- Gradient Boost & Ada Boost
طبقه بندی الگوریتم های مختلف یادگیری ماشین
الگوریتمهای مختلفی در حوزه یادگیری ماشین و هوش مصنوعی در سالهای اخیر ایجاد یا بهبود یافته اند که برای هر فردی که قصد کار حرفه ای در این حوزه را دارد، آشنایی و تسلط بر آنها و مفاهیم پایه هر کدام و نیز استفاده از آنها در کاربردهای عملی، جزء ضروریات است.
در سال ۲۰۰۷ یک مقاله با عنوان ده الگوریتم برتر حوزه داده کاوی در دنیا توسط دانشگاه ورمونت مطرح شد که نسخه فارسی شده و حتی آماده انتشار به صورت کتاب آنرا هم در ایران داریم . مقاله فارسی را می توانید از این لینک دانلود نمایید.
10 الگریتم برترین های داده کاوی
رمز : behsanandish.com
این ده الگوریتم عبارتند از :
در سال ۲۰۱۱، در سایت پرسش و پاسخ معروف Qura در پاسخ به سوالی که ده الگوریتم برتر داده کاوی را پرسیده بود، موارد زیر توسط کاربران برشمرده شده اند :
- Kernel Density Estimation and Non-parametric Bayes Classifier
- K-Means
- Kernel Principal Components Analysis
- Linear Regression
- Neighbors (Nearest, Farthest, Range, k, Classification)
- Non-Negative Matrix Factorization
- Dimensionality Reduction
- Fast Singular Value Decomposition
- Decision Tree
- Bootstapped SVM
- Decision Tree
- Gaussian Processes
- Logistic Regression
- Logit Boost
- Model Tree
- Naïve Bayes
- Nearest Neighbors
- PLS
- Random Forest
- Ridge Regression
- Support Vector Machine
- Classification: logistic regression, naïve bayes, SVM, decision tree
- Regression: multiple regression, SVM
- Attribute importance: MDL
- Anomaly detection: one-class SVM
- Clustering: k-means, orthogonal partitioning
- Association: A Priori
- Feature extraction: NNMF
و در سال ۲۰۱۵ این لیست به صورت زیر در آمده است :
- Linear regression
- Logistic regression
- k-means
- SVMs
- Random Forests
- Matrix Factorization/SVD
- Gradient Boosted Decision Trees/Machines
- Naive Bayes
- Artificial Neural Networks
- For the last one I’d let you pick one of the following:
- Bayesian Networks
- Elastic Nets
- Any other clustering algo besides k-means
- LDA
- Conditional Random Fields
- HDPs or other Bayesian non-parametric model
سایت DataFloq اخیراً یک طبقه بندی گرافیکی از الگوریتم های ضروری یادگیری ماشین ارائه کرده است که به صورت طبقه بندی شده ، این الگوریتم ها را فهرست کرده است :

این طبقه بندی را به صورت نقشه ذهن یا Mind Map هم می توانیم مشاهده کنیم :

منبع