بایگانی‌های آموزش عمومی پردازش تصویر و بینایی ماشین

در علم آمار هیستوگرام یا بافت‌نگار یک نمودار ستونی و پله‌ای برای نشان دادن داده‌ها است.

برای نمونه بافت‌نگار فراوانی، نمودار مستطیلی با پایه‌ای به پهنای یک واحد بر روی هر مقدار مشاهده شده‌است که ارتفاع هر ستون آن برابر با فراوانی داده مورد نظر همخوانی دارد

نمودار بافت‌نگار همانند نمودار ستونی است و یگانه اختلافی که بین این دو وجود دارد، نمایش ستون‌هاست.

در پردازش تصویرها بافت‌نگار تصویر نموداری است که توسط آن تعداد پیکسل‌های هر سطح روشنایی در تصویر ورودی مشخص می‌شود.

بافت‌نگار

One of the Seven Basic Tools of Quality

معرفی‌کننده نخست : کارل پیرسون

کاربرد : توزیع احتمال. To roughly assess the of a given variable by depicting the frequencies of observations occurring in certain ranges of values

نمونه‌ای از یک بافت‌نگار

در عکاسی

بافت‌نگار (هیستوگرام) در عکاسی، به عنوان یک عملگر کاربردی مصطلح است و یکی از ابزارهای مفید و کارآمد در دوربین‌های عکاسی دیجیتالبه‌شمار می‌رود. که با این نام (برای این عملگر) چنین در بین کاربران مصطلح شده‌است و ارتباطی با کارکرد علمی آن ندارد.

بافت‌نگار به نموداری گفته می‌شود که فراوانی عناصری که در محور افقی آن قرار دارند را در محور عمودی نشان می‌دهد. بافت‌نگار عکس، شدت نور را، از کمترین مقدار تا بیشترین مقدار، در محور افقی و تعداد پیکسل‌های هرکدام از آن‌ها را در محور عمودی نشان می‌دهد.
توجه به بافت‌نگار، راه بسیار خوبی برای کنترل نوردهیدوربین و تصویر بوجود آمده‌ است

منبع

هیستوگرام تصویر

یک هیستوگرام تصویر از یک تصویر T1 فیلتر شده از یک مغز، پردازش شده توسط نرم‌افزار مانگو. ۳ قلهٔ مشهود در این نمودار ستونی متعلق به ماده سفید، ماده خاکستری، و CSF (آب نخاع) می‌باشند. دم سمت چپ متعلق به بقایای جمجمه و چربی پس از حذف به روش پردازش (فیلترینگ) بدست آمده است.

در یک تصویر دیجیتال، مقادیر پیکسل‌ها بیانگر ویژگی‌های آن تصویر (مانند میزان روشنایی تصویر و وضوح تصویر) است. هیستوگرام یک تصویر در حقیقت بیان گرافیکی میزان روشنایی تصویر می‌باشد. مقادیر روشنایی (برای مثال ۰-۲۵۵) در طول محور X بیان شده و میزان فراوانی هر مقدار در محور Y بیان می‌گردد.

تصویر ۸ بیتی (۰-۲۵۵) در بالا و هیستوگرام همان تصویر در پایین. محور افقی بین ۰ تا ۲۵۵ و محور قائم نشانگر تعداد پیکسل‌ها است.

تصویری که هیستوگرام زیر از آن گرفته شده‌است

منبع

نمودار هیستوگرام تصویر نموداری است که در آن تعداد پیکسل های هر سطح روشنایی در تصویر ورودی مشخص می شود. فرض کنید تصویر ورودی یک تصویر Grayscale با 256 سطح روشنایی باشد ، بنابراین هریک از پیکسل های تصویر در شدت روشنایی در بازه [0..255] می توانند داشته باشند. برای به دست آوردن هیستوگرام تصویر ، با پیمایش پیکسل های تصویر ، تعداد پیکسل های هر سطح روشنایی را محاسبه می کنیم .

هیستوگرام نرمال نیز از تقسیم کردن مقادیر هیستوگرام به تعداد کل پیکسل های تصویر به دست می آید. نرمال سازی هیستوگرام موجب می شود که مقادیر هیستوگرام در بازه [0,1] قرار گیرند. شکل زیر تصویری را به همراه هیستوگرام نرمال آن نشان می دهد :

تعدیل هیستوگرام ( Histogram Equalization )

به تصویر زیر توجه کنید :

تصویر دانه های برنج با کنتراست پایین هیستوگرام تصویر دانه های برنج با کنتراست پایین

همانطور که از شکل و هیستوگرام تصویر مشخص است ، کنتراست تصویر فوق پایین می باشد. بدین مفهوم که اختلاف کمترین و بیشترین شدت روشنایی کم است. با تعدیل سازی هیستوگرام تصویر با کنتراست پایین ، تصویری با کنتراست بالا به دست می آید :

شکل فوق تصویر قبلی پس از انجام تعدیل سازی هیستوگرام را نشان می دهد. الگوریتم زیر روش تعدیل سازی یکنواخت هیستوگرام را نشان می دهد :

1 ) هیستوگرام تصویر را محاسبه می کنیم. فرض کنید مقادیر هیستوگرام در آرایه hist قرار گیرد.

2 ) با استفاده از فرمول زیر فراوانی هیستوگرام را محاسبه می کنیم :

histCum[ i ] = histCum[ i-1 ] + hist[ i ]

3 ) از فرمول زیر استفاده کرده و هیستوگرام تعدیل شده را محاسبه می کنیم :

eqHist[i] = Truncate( [(L * histCum[i]) – N]/N )

که در این فرمول L تعداد سطوح خاسکتری و N تعداد کل پیکسل ها را نشان می دهد

4 ) در مرحله نهایی مقادیر جدید پیکسل ها را به صورت زیر مقدار دهی می کنیم :

Result[ i , j ] = eqHist[ input[ i , j ] ]

که Result تصویر خروجی و input تصویر ورودی را نشان می دهد

منبع

هیستوگرام به معنی نشان دادن میزان فراوانی مقادیر بر روی نمودار است. در تصویر شما با شدت نور سر و کار دارید که بازه آن برای تصویر خاکستری از 0 تا 255 است یعنی تعداد level ها یا bin ها 256 تا است.

حال اگر تصویر رنگی باشد 3 کانال مجزای خاکستری خواهد بود.

برای محاسبه هیستوگرام می بایست تعداد تکرار یا همون فرکانس شدت ها رو در تصویر محاسبه کرد یعنی تعداد هر شدت نور را در تصویر شمارش کرده و در level یا bin مربوط قرار داد.

نکته ای که وجود دارد این است که همیشه قرار نیست 256 تا bin وجود داشته باشد. می توان 10 تا bin تعریف کرد و در هر بازه هر bin فراوانی ها را با هم جمع کرد.

در OpenCV برای محاسبه هیستوگرام می توان از تابع calcHist استفاده کرد. تابع calcHist می تواند در چند کانال یا چند بعد هم هیستوگرام را محاسبه می کند و بایستی در هر کانال تعداد bin ها را مشخص کرد.

یک مثال عملی از کاربردهای هیستوگرام که ی توان بیان کرد: در فریم های متوالی هیستوگرام را مقایسه کنید مثلا شما قصد دارید چهره شخص را بدون detection در هر فریم تعقیب کنید برای اینکار می توانید از انواع ویژگی های تصویر استفاده کنید از جمله آنها انتقال اطلاعات گردایان بر روی هیستوگرام و هم انتقال اطلاعات شدت نور در کانال ها بر روی هیستوگرام و سپس مقایسه این هیستوگرام با فریم های قبلی.

منبع

منابع

دسامبر 24, 2019/1 دیدگاه/توسط daliri

مجموعه مقالات فیلتر گابور (Gabor Filter) قسمت 2

آموزش عمومی پردازش تصویر و بینایی ماشین

9.آشکار سازی صورت با استفاده فیلترهای گابور و شبکه های عصبی

ﭼﻜﻴﺪه: در این مقاله، روشی قدرتمند برای آشکارسازی صورت از زوایای مختلف با استفاده از ترکیب فیلترهای گابور و شبکه ی عصبی بیان می شود. در ابتدا رابطه ی ریاضی تولید فیلتر گابور ورد بررسی قرار می گیرد و در مرحله بعد با برسسی 75 بانک فیلتر مختلف، محدوده مقادیر پارامترهای مؤثر در تولید فیلتر گابور مشخص شده و سپس بهترین مقدار برای آنها به دست می آید. شبکه ی عصبی مورد استفاده در این نوع مقاله از نوع پیش خور با روش بازگشتی است و بردار ورودی این شبکه عصبی از کانوالو تصویر با تنها یک فیلتر گابور با زاویه و فرکانس در خوزه فرکانس به دست می آید. الگوریتم پیشنهادی در این مقاله روی 550 تصویر از 2 پایگاه تصویر فرت با پس زمینه ساده و مارکوس وبر با پس زمینه پیچیده آزمایش شده و دقت آشکارسازی آن به ترتیب 98/4% و 95% است. همچنین به کمک الگوریتم ویولا جونز ناحیه صورت را در 550 نمونه تصویر به دست آورده و مقایسه ای بین نتایج به دست آمده از الگوریتم ویولاجونز و آلگوریتم پیشنهادی آورده می شود.

کلمات کلیدی: آشکار سازی صورت، شبکه عصبی، فیلتر گابور، ویژگی های گابور

فایل PDF – در 13 صفحه- نویسنده : ﻣﺤﻤﻮد ﻣﺤﻠﻮﺟﻲ و رضا محمدیان

آشکار سازی صورت با استفاده فیلترهای گابور و شبکه های عصبی

پسورد فایل : behsanandish.com

10.بهبود روش های ناحیه بندی تصاویر MRI مغز انسان با استفاده از عملگر گابور

فایل PDF – در 15 صفحه- نویسنده : فرزاد فلاحی

بهبود روش های ناحیه بندی تصاویر MRI مغز انسان با استفاده از عملگر گابور

پسورد فایل : behsanandish.com

11. بهبود سیستم های ایمنی برای تشخیص اجسام در تصویرهای پرتونگاری بار

چکیده: بازرسی چشمی بار در فرودگاهها و مراکز حساس مستلزم صرف زمان زيادی است و اجسام در بسياری از موارد خصوصاً زمانی که در موقعيت و زاويههای خاصی قرار گرفته باشند قابل شناسايی با بازرسیهای سريع چشمی نيستند. امروزه از دستگاههای تصويربرداری پرتو ايکس برای تشخيص اجسام در بار استفاده میشود. تصاوير پرتونگاری حاصل به علت پراکندگی فوتونی دارای ميزانی از مهآلودگی هستند و گاهی تشخيص دقيق اجسام با مشکل مواجه میشود. روشهای پردازش تصوير میتوانند به بهبود کنتراست و در نتيجه بهتر شدن قابليت تشخيص اجسام کمک کنند. در پرتونگاری بار سطح نويز و پراکندگی در تصويرهای مختلف با هم تفاوت زيادی دارند که اين موضوع ضرورت استفاده از روشهای پردازش تصوير خودکار را ايجاب میکند. در اين پژوهش از دو روش موجک و صافی گابور با سطح آستانهی خودکار استفاده شده است. نتايج حاصل نشان میدهد تصويرهای بازسازی شده اگرچه در جزييات دارای اختلافاتی هستنند ولی در ميزان تشخيص اجسام توسط افراد تفاوت زيادی ندارند. در هر دو روش کنتراست و قابليت تشخيص اجسام نسبت به تصويرهای اوليه بهبود قابل ملاحظهای يافته است. زمان اجرای الگوريتم موجک گسسته حدود يک هشتم زمان اجرای صافی گابور است که با توجه به اهميت سرعت پردازش تصوير در بازرسی بار برتری قابل ملاحظهای است.

کلید واژهها: پرتونگاری بار،سیستم بازرسی بار،پرتو ایکس، روش موجک گسسته، فیلتر گابور

فایل PDF – در 13 صفحه- نویسندگان : سمانه شیخ ربیعی، بهروز رکرک، عفت یاحقی، بهنام آرضابک

بهبود سیستم های ایمنی برای تشخیص اجسام در تصویرهای پرتونگاری بار

پسورد فایل : behsanandish.com

12. ﺑﻬﺒﻮد کیفیت تصویر اﺛﺮاﻧﮕﺸﺖ ﺑﺎ اﺳﺘﻔﺎده از فیلتر بانک ﮐﻤﺎﻧﯽ گابور

ﭼﮑﯿﺪه: ﺗﺄﯾﯿﺪ و ﺷﻨﺎﺳﺎﯾﯽ ﻫﻮﯾﺖ از روی ﺗﺼﻮﯾﺮ اﺛﺮاﻧﮕﺸﺖ ارﺗﺒﺎط ﻣﺴﺘﻘﯿﻤﯽ ﺑﺎ ﮐﯿﻔﯿﺖ اﯾﻦ ﺗﺼـﻮﯾﺮ دارد. در اﯾـﻦ ﻣﻘﺎﻟـﻪ روش ﺟﺪﯾـﺪی ﺑﺮای ﺑﻬﺒﻮد ﮐﯿﻔﯿﺖ ﺗﺼﻮﯾر اﺛﺮ اﻧﮕﺸﺖ ﺑﺎ اﺳﺘﻔﺎده از ﻓﯿﻠﺘﺮ ﺑﺎﻧﮏ اﺳـﺖ ﮐﻤﺎﻧﯽ ﮔـﺎﺑﻮر اراﺋـﻪ ﺷـﺪه است. ﻓﯿﻠﺘـﺮ ﺑﺎﻧـﮏ ﮐﻤـﺎﻧﯽ ﮔـﺎﺑﻮر در ﺣﻘﯿﻘﺖ ﻧﻮﻋﯽ ﻓﯿﻠﺘﺮ ﺑﺎﻧﮏ ﮔﺎﺑﻮر اﺳﺘﺎﻧﺪارد ﻣﺘﺒﺤﺮ ﺷﺪه ﺑﺮای اﺳﺘﻔﺎده روی ﺗﺼﺎوﯾﺮ اﺛﺮ اﻧﮕﺸﺖ می ﺑﺎﺷﺪ. ارزﯾﺎﺑﯽ ﻣﯿـﺰان ﺗﻮﻓﯿـﻖ روش در بهبود ﮐﯿﻔﯿﺖ ﺗﺼﺎوﯾﺮ اﺛﺮ اﻧﮕﺸﺖ ﺑﻪ دو روش اﻧﺠﺎم ﺷﺪه است. در روش اول، ﻣﻘﺎﯾﺴﻪ ﺑﯿﻦ ﺗﺼﺎوﯾﺮ اﺻـﻠﯽ و ﺗﺼـﺎوﯾﺮ ﺑﻬﺒﻮد ﯾﺎﻓﺘﻪ ﺑﺮاﺳﺎس ﻧﺘﺎﯾﺞ ﺑﺪﺳﺖ آﻣﺪه از ارزﯾﺎﺑﯽ ﺗﺄﯾﯿﺪ و ﺷﻨﺎﺳﺎﯾﯽ ﻫﻮﯾﺖ ﺻﻮرت ﭘﺬﯾﺮﻓﺘﻪ اﺳﺖ که ﺳﯿﺴﺘﻢ ﺗﺸﺨﯿﺺ ﻫﻮﯾـﺖ ﭘﯿﺸﻨﻬﺎدی ﻣﺒﺘﻨﯽ ﺑﺮ معیار ﻫﻤﺒﺴﺘﮕﯽ ﻫﯿﺴﺘﻮﮔﺮام ﻧﺮﻣﺎﻟﯿﺰه ﺷﺪه ویژگی های تصویر آماری باینری شده (BSIF) است. در روش دوم، از ﻣﻌﯿﺎر ﻧﺴﺒﺖ ﺳﯿﮕﻨﺎل ﺑﻪ ﻧﻮﯾﺰ ﺑﯿﺸﯿﻨﻪ (PSNR) به منظور ارزﯾﺎﺑﯽ میزان بهبود ﮐﯿﻔﯿﺖ، اﺳﺘﻔﺎده ﺷـﺪه است. دو ﭘﺎﯾﮕـﺎه DBI و DBII برای اجرای روش و ارزیابی نتایج مورد استفاده ﻗﺮار گرفته اﻧﺪ .ﻧﺮخ ﺗﺴﺎوی ﺧﻄﺎی (EER) ﺗﺄﯾﯿﺪ ﻫﻮﯾـﺖ ﺑﺮای ﺗﺼﺎوﯾﺮ اﺻﻠﯽ از (ﺑﻪ ترتیب % ۱۵/۸۹ و ۱۱/۷۰%) به ( % ۱۱/۳۵ و ۸/۰۰%) ﺑـﺮای ﺗﺼـﺎوﯾﺮ ﺑﻬﺒـﻮد ﯾﺎﻓﺘـﻪ کاهش ﯾﺎﻓﺘﻪ اﺳﺖ .ﺑﺮای ﺗﺸﺨﯿﺺ ﻫﻮﯾﺖ ﻧﯿﺰ ﻧﺮخ ﻣﺮﺗﺒﻪ اول ﻣﯿﺰان ﺑﺎزﺷﻨﺎﺳـﯽ ﺻـﺤﯿﺢ ﺑـﺮای ﺗﺼـﺎوﯾﺮ اصلی از مقادیر( ۶۹/۲۸% و ۷۱/۱۶ %) به (۷۸/۸۰% و ۸۱/۷۰ %) ﺑﺮای ﺗﺼﺎوﯾﺮ ﺑﻬﺒﻮد ﯾﺎﻓﺘﻪ اﻓﺰاﯾﺶ ﯾﺎﻓﺘﻪ است. ﻣﯿﺰان متوسط PSNR ﻣﺮﺑﻮط ﺑﻪ ﺗﺼﺎوﯾﺮ ﺑﻬﺒﻮد ﯾﺎﻓﺘﻪ ﻧﯿﺰ از ﻣﻮرد ﻣﺸﺎﺑﻪ ﺑﺮای ﺗﺼﺎوﯾﺮ اﺻﻠﯽ ﺑﯿﺸﺘﺮ اﺳﺖ.

ﮐﻠﯿﺪ واژهﻫﺎ: ﮐﯿﻔﯿﺖ ﺗﺼﻮﯾﺮ، ﻓﯿﻠﺘﺮﺑﺎﻧﮏ اﺛﺮاﻧﮕﺸﺖ، ﺑﻬﺒﻮد ﮐﻤﺎﻧﯽ ﮔﺎﺑﻮر

فایل PDF – در 17 صفحه- نویسندگان : مهران تقی پور گرجی کلایی، سید محمد رضوی و ناصر مهرشاد

ﺑﻬﺒﻮد کیفیت تصویر اﺛﺮاﻧﮕﺸﺖ ﺑﺎ اﺳﺘﻔﺎده از فیلتر بانک ﮐﻤﺎﻧﯽ گابور

پسورد فایل : behsanandish.com

13. تشخیص چهره با استفاده از PCA و فیلتر گابور

فایل PDF – در 8 صفحه- نویسندگان : حمیدرضا قجر، محسن سریانی و عباس کوچاری

تشخیص چهره با استفاده از PCA و فیلتر گابور

پسورد فایل : behsanandish.com

14. تعیین توزیع دانه بندی سنگ دانه های بتن و آسفالت با استفاده از استخراج ویژگی های گابور و شبکه های عصبی

چکیده: توزیع ابعادی سنگدانه های تشکیل دهنده بتن و آسفالت، از مهمترین پارامترها در کنترل طرحهای اختلاط بتن و آسفالت است که میتواند بر کیفیت نهایی، مقاومت و دوام بتن و آسفالت تاثیر گذار باشد. بهمنظور ارزیابی درصد اختلاط سنگدانه ها، روش پردازش تصویری دیجیتال یک روش غیر مستقیم، سریع و قابل اعتماد است. در این تحقیق بر پایه یکی از روشهای استخراج ویژگیهای دیداری تصویر (فیلترهای گابور) و استفاده از شبکه های عصبی، الگوریتمی جهت تعیین توزیع دانه بندی تصاویر سنگدانه های تشکیل دهنده بتن و آسفالت ارائه شده است. تعداد 100 تصویر از سنگدانه های تشکیل دهنده بتن و آسفالت برای آموزش شبکه عصبی به کار برده شد. سپس نتایج حاصله با نتایج تخمین خودکار دانه بندی سنگدانه ها در نرم افزار Split-Desktop و همچنین تجزیه سرندی مقایسه شد.نتایج به دست آمده بیانگر یک بهبود کلی در ارزیابی توزیع اندازه سنگدانه های تشکیل دهنده بتن و آسفالت و کاهش خطای 67% با استفاده از روش پیشنهادی نسبت به تخمین خودکار نرم افزار Split-Desktop است. همچنین در ارزیابی اندازه های F10 تا F100، روش پیشنهادی بهبود 62% را نشان داد.

واژه های کلیدی: توزیع دانه بندی، سنگدانه های بتن و آسفالت، استخراج ویژگی تصویر، فیلترهای گابور، شبکه های عصبی.

فایل PDF – در 14 صفحه- نویسندگان : هادی یعقوبی، حمید منصوری، محمد علی ابراهیمی فرسنگی و حسین نظام آبادی پور

تعیین توزیع دانه بندی سنگ دانه های بتن و آسفالت با استفاده از استخراج ویژگی های گابور و شبکه های عصبی

پسورد فایل : behsanandish.com

15. خوشه بندی سبک نگارش دست نوشته برون خط فارسی

چکیده– ﻫﺪﻑ ﺍﻳﻦ ﭘﺎﻳﺎﻥ ﻧﺎﻣﻪ، ﻳﺎﻓﺘﻦ ﻭ ﺍﺳﺘﺨﺮﺍﺝ ﻭﻳﮋﮔﻲ ﻫﺎﻳﻲ ﺍﺳﺖ ﮐﻪ ﺑﺮ ﻣﺒﻨﺎﻱ ﺁﻥ ﺑﺘﻮﺍﻥ ﺩﺳﺖ ﺧﻂ ﻓﺎﺭﺳﻲ ﺭﺍ ﺧﻮﺷﻪ ﺑﻨﺪﻱ ﮐﺮﺩ .ﺩﺭ ﺍﻳﻦ ﮐﺎﺭ، ﺩﺭ ﺍﺑﺘﺪﺍ ﺑﺮ ﺭﻭﻱ ﻭﻳﮋﮔﻲ ﻫﺎﻱ ﻣﺒﺘﻨﻲ ﺑﺮ ﺑﺎﻓﺖ، ﺗﻤﺮﮐﺰ ﺷﺪﻩ ﺍﺳﺖ .ﺍﻳﻦ ﻭﻳﮋﮔﻲ ﻫﺎ ﺷﺎﻣﻞ ﺩﻭ ﺩﺳﺘﻪ ﻭﻳﮋﮔﻲ ﺁﻣﺎﺭﻱ ﻣﺎﺗﺮﻳﺲ ﺑﺎﻫﻢ ﺁﻳﻲ ﻭ ﻭﻳﮋﮔﻲ ﻣﺒﺘﻨﻲ ﺑﺮ ﺗﺒﺪﻳﻞ ﮔﺎﺑﻮﺭ ﺍﺳﺖ .ﺑﺮﺍﻱ ﺍﺳﺘﺨﺮﺍﺝ ﺍﻳﻦ ﻭﻳﮋﮔﻲﻫﺎ، ﻳﮏ ﺑﺎﻓﺖ ﻣﻨﺎﺳﺐ ﺩﺭ ﺍﺑﻌﺎﺩ ۱۰۲۴×۱۰۲۴ ﻣﺴﺘﻘﻞ ﺍﺯ ﻣﺤﺘﻮﺍﻱ ﺳﻨﺪ، ﺍﺯ ﺗﺼﻮﻳﺮ ﺩﺳﺘﻨﻮﺷﺘﻪ ﺍﻳﺠﺎﺩ ﻣﻲ ﺷﻮﺩ .ﺍﺯ ﻭﻳﮋﮔﻲ ﻫﺎﻱ ﺩﻳﮕﺮﻱ ﮐﻪ ﺩﺭ ﺍﻳﻦ ﮐﺎﺭ ﺍﺯ ﺁﻥ ﻫﺎ ﺍﺳﺘﻔﺎﺩﻩ ﺷﺪﻩ ﺍﺳﺖ، ﺗﻌﺪﺍﺩﻱ ﻭﻳﮋﮔﻲ ﺳﺎﺧﺘﺎﺭﻱ ﻣﺒﺘﻨﻲ ﺑﺮ ﻣﻨﺤﻨﻲ ﭘﻴﺮﺍﻣﻮﻧﻲ ﺍﺳﺖ .ﺍﻳﻦ ﻭﻳﮋﮔﻲ ﻫﺎ ﺭﺍ ﺍﺯ ﻫﺮ ﻳﮏ ﺍﺯ ﺗﺼﺎﻭﻳﺮ ﻣﻮﺟﻮﺩ ﺩﺭ ﻳﮏ ﻣﺠﻤﻮﻋﻪ ﺩﺍﺩﻩ ﺍﺯ 97 ﺩﺳﺘﻨﻮﺷﺘﻪ ﻓﺎﺭﺳﻲ ﮐﻪ ﺩﺍﺭﺍﻱ ﻣﺘﻮﻥ ﻣﺘﻔﺎﻭﺗﻲ ﺑﻮﺩﻧﺪ، ﺍﺳﺘﺨﺮﺍﺝ ﮐﺮﺩﻳﻢ ﻭ ﺍﺯ ﺍﻟﮕﻮﺭﻳﺘﻢ k ﻣﻴﺎﻧﮕﻴﻦ ﻭ ﺷﺒﮑﻪ ﻋﺼﺒﻲ ﻧﮕﺎﺷﺖ ﻭﻳﮋﮔﻲ ﺧﻮﺩ ﺳﺎﻣﺎﻥ، ﺑﺮﺍﻱ ﺧﻮﺷﻪ ﺑﻨﺪﻱ ﺍﻳﻦ ﻭﻳﮋﮔﻲ ﻫﺎ ﺍﺳﺘﻔﺎﺩﻩ ﺷﺪﻩ ﺍﺳﺖ.

ﺑﺮﺍﻱ ﺍﺭﺯﻳﺎﺑﻲ ﺍﻳﻦ ﻭﻳﮋﮔﻲ ﻫﺎ، ﻳﮏ ﺭﻭﺵ ﺍﺭﺯﻳﺎﺑﻲ ﺑﺮ ﻣﺒﻨﺎﻱ ﺍﻟﮕﻮﺭﻳﺘﻢ ﺧﻮﺷﻪ ﺑﻨﺪﻱ k ﻣﻴﺎﻧﮕﻴﻦ، ﻃﺮﺍﺣﻲ ﮐﺮﺩﻩ ﺍﻳﻢ .ﺩﺭ ﺍﻳﻦ ﺍﻟﮕﻮﺭﻳﺘﻢ ﺍﺯ ﻣﻌﻴﺎﺭ ﻣﻘﺎﻳﺴﻪ ﺑﺎﻳﻨﺮﻱ ﮊﺍﮐﺎﺭﺩ ﺍﺳﺘﻔﺎﺩﻩ ﮐﺮﺩﻩ ﺍﻳﻢ، ﻫﻢ ﭼﻨﻴﻦ ﺑﺮﺍﻱ ﻣﺤﺎﺳﺒﻪ ﻣﺮﺍﮐﺰ ﺧﻮﺷﻪ ﺩﺭ ﻫﺮ ﺩﻭﺭﻩ ﺗﮑﺮﺍﺭ ﺍﺯ ﺍﻟﮕﻮﺭﻳﺘﻢ k ﻣﻴﺎﻧﮕﻴﻦ، ﺍﺯ ﺭﻭﺵ ﺍﻧﺘﺨﺎﺏ ﺩﺍﺩﻩ ﭼﺮﺥ ﺭﻭﻟﺖ، ﺑﻬﺮﻩ ﮔﺮﻓﺘﻪﺍﻳﻢ.

ﻧﺘﺎﻳﺞ ﺑﺪﺳﺖ ﺁﻣﺪﻩ، ﻧﺸﺎﻥ ﻣﻲ ﺩﻫﺪ ﺑﺎ ﺗﺮﮐﻴﺐ ﺩﻭ ﻧﻮﻉ ﺍﺯ ﻭﻳﮋﮔﻲ ﻫﺎﻱ ﻣﺒﺘﻨﻲ ﺑﺮ ﻣﻨﺤﻨﻲ ﭘﻴﺮﺍﻣﻮﻧﻲ، ﻧﺮﺥ ﺧﻮﺷﻪ بندی 75 ﺩﺭﺻﺪ ﺍﺳﺖ ﮐﻪ ﻧﺴﺒﺖ ﺑﻪ ﺳﺎﻳﺮ ﺭﻭﺵﻫﺎﻱ ﻣﻮﺭﺩ ﺍﺳﺘﻔﺎﺩﻩ ﺩﺭ ﺍﻳﻦ ﮐﺎﺭ، ﻧﺮﺥ ﺑﻬﺘﺮﻱ ﺭﺍ ﺩﺭ ﺑﺮﺩﺍﺷﺘﻪ ﺍﺳﺖ .

ﮐﻠﻴﺪ ﻭﺍﮊﻩ: ﺳﺒﮏ ﻧﮕﺎﺭﺵ، ﺧﻮﺷﻪ ﺑﻨﺪﻱ، ﺑﺎﻓﺖ، ﻓﻴﻠﺘﺮ ﮔﺎﺑﻮﺭ، ﻣﺎﺗﺮﻳﺲ ﺑﺎ ﻫﻢ ، ﺁﻳﻲ، ﻣﻨﺤﻨﻲ ﭘﻴﺮﺍﻣﻮﻧﻲ، ﮊﺍﮐﺎﺭﺩ ﭼﺮﺥ ﺭﻭﻟﺖ

فایل PDF – در 20 صفحه- نویسنده : فاطمه ولایتی

خوشه بندی سبک نگارش دست نوشته برون خط فارسی

پسورد فایل : behsanandish.com

16. شاخص گذاری بر روی تصاویر با استفاده از موجک های گابور و ممان های لژاندر

چکیده- در این مقاله، یک سیستم جدید شاخص گذاری و بازیابی تصاویر (CBIR) با استفاده از موجک های گابور و ممان های لژاندار پیشنهاد گردیده است. از انجائیکه موجک های گایور قادر به استخراج مطلوب اطلاعات خطوط و لبه های تصاویر در مقیاس ها و درجات تفکیک مختلف می باشند و از طرف دیگر، این تبدیل تنها تابعی است که می تواند حد تئوری دقت تفکیک توأم اطلاعات در هر حوزه مکان و فرکانس را حاصل نماید، در اینجا از آن به منظور تشخیص محتوای بصری تصاویر به کار گرفته شده است. هم چنین ممانهای لژاندار جهت بهبود نتایج حاصل از عمل بازیابی الگوریتم استفاده شده اند. کوچکی نسبی طول بردار ویژگی (58)، از مزایای این روش می باشد که عمل بازیابی را تسریع می بخشد. همچنین به دلیل آنکه اطلاعات رنگ تصاویر مورد استفاده قرار نمی گیرند، الگوریتم قادر به تشخیص تصاویر مشابه با رنگ های متفاوت نیز خواهد بود. نتایج حاصل از اجرای این سیستم، راندمان بالای آن را در تشخیص تصاویر مشابه مورد تأییید قرار می دهد.

واژگان کلیدی: شاخص گذاری و بازیابی تصاویر، فیلترهای گابور، ممانهای لژاندار، سیستم های مستقل از رنگ، پردازش تصویر.

فایل PDF – در 8 صفحه- نویسندگان : اسماعیل فرامرزی، ابوالقاسم صیادیان، علیرضا احمدیان

شاخص گذاری بر روی تصاویر با استفاده از موجک های گابور و ممان های لژاندر

پسورد فایل : behsanandish.com

17. طراحی بخش دریافت و پردازش تصویر برای یک پروتز بینایی

ﭼﮑﯿﺪه ﺗﻼش ﻫﺎ ﺑﺮاي ﺗﺤﻘﻖ ﭘﺮوﺗﺰﻫﺎي ﺑﯿﻨﺎﯾﯽ از دﻫﻪ ﮔﺬﺷﺘﻪ آﻏﺎز ﺷﺪه اﺳﺖ. ﭘﺮوﺗﺰﻫﺎي ﺑﯿﻨﺎﯾﯽ ﺟﺎﻧﺸﯿﻨﯽ ﺑﺮاي ﺳﯿﺴﺘﻢ ﺑﯿﻨﺎﯾﯽ ﻣﻌﯿﻮب ﻫﺴﺘﻨﺪ ﺗﺎ ﺑﺘﻮاﻧﻨﺪ ﺑﯿﻨﺎﯾﯽ را ﺑﻪ اﻓﺮاد ﻧﺎﺑﯿﻨﺎ ﺑﺎزﮔﺮداﻧﻨﺪ. ﺑﺎ وﺟﻮد اﯾﻦ ﺗﻼش ﻫﺎ، داﻧﺸﻤﻨﺪان ﻣﻮﻓﻖ ﺑﻪ ﺳﺎﺧﺖ ﭘﺮوﺗﺰ ﺑﯿﻨﺎﯾﯽ ﮐﻪ ﺑﺘﻮاﻧﺪ ﺟﺎﻧﺸﯿﻦ ﻣﻨﺎﺳﺒﯽ ﺑﺮاي ﺳﯿﺴﺘﻢ ﺑﯿﻨﺎﯾﯽ ﺷﻮد، ﻧﺸﺪه اﻧﺪ.
ﭘﺮدازش ﺗﺼﻮﯾﺮ در ﭘﺮوﺗﺰﻫﺎي ﺑﯿﻨﺎﯾﯽ ﺑﺮاي اﻓﺰاﯾﺶ درك ﺗﺼﻮﯾﺮي ﻓﺮد ﻧﺎﺑﯿﻨﺎ از ﻣﺤﯿﻂ اﻃﺮاف ﻫﻨﮕﺎم اﺳﺘﻔﺎده از ﭘﺮوﺗﺰ ﺑﯿﻨﺎﯾﯽ ﮐﺎرﺑﺮد دارد. در اﯾﻦ رﺳﺎﻟﻪ ﯾﮏ روش ﺟﺪﯾﺪ ﺑﺮ ﻣﺒﻨﺎي ﻓﯿﻠﺘﺮ ﮔﺎﺑﻮر و ﺗﺒﺪﯾﻞ ﮐﺴﯿﻨﻮﺳﯽ ﮔﺴﺴﺘﻪ ﺑﺮاي اﺳﺘﻔﺎده درﯾﮏ ﺳﯿﺴﺘﻢ ﭘﺮوﺗﺰ ﺑﯿﻨﺎﯾﯽ ﻣﻌﺮﻓﯽ ﺷﺪه اﺳﺖ. در اداﻣﻪ اﻟﮕﻮرﯾﺘﻢ ﻫﺎي ﺟﺪﯾﺪ و ﭘﺮدازش ﺗﺼﻮﯾﺮ ﭘﯿﺸﻨﻬﺎد ﺷﺪه در اﯾﻦ رﺳﺎﻟﻪ ارزﯾﺎﺑﯽ و ﻣﻘﺎﯾﺴﻪ ﺷﺪه اﻧﺪ و اﻟﮕﻮرﯾﺘﻢ ﭘﯿﺸﻨﻬﺎد ﺷﺪه ﺑﺎ 78 % ﻧﺮخ ﺑﺎزﺷﻨﺎﺳﯽ، ﮐﺎراﯾﯽ ﺑﻬﺘﺮي ﻧﺴﺒﺖ ﺑﻪ دﯾﮕﺮ روش ﻫﺎ داﺷﺘﻪ اﺳﺖ. ﺑﻪ ﻣﻨﻈﻮر ارزﯾﺎﺑﯽ اﻟﮕﻮرﯾﺘﻢ ﻫﺎي ﭘﯿﺸﻨﻬﺎدي و ﻫﻤﭽﻨﯿﻦ ﺑﺮاي ﺑﻪ ﮐﺎر ﮔﯿﺮي در ﻧﻤﻮﻧﻪ اوﻟﯿﻪ ﺳﯿﺴﺘﻢ ﭘﺮوﺗﺰ ﺑﯿﻨﺎﯾﯽ، اﯾﻦ ﭘﺮدازش ﻫﺎ ﺑﻪ ﺻﻮرت ﺳﺨﺖ اﻓﺰاري ﭘﯿﺎده ﺳﺎزي و آزﻣﺎﯾﺶ ﺷﺪه اﻧﺪ. ﺑﺮاي ﭘﯿﺎده ﺳﺎزي ﺳﺨﺖ اﻓﺰاري اﻟﮕﻮرﯾﺘﻢ ﻫﺎي ﭘﺮدازﺷﯽ از ﺑﺮد MINI2440 اﺳﺘﻔﺎده ﺷﺪه اﺳﺖ. ﺑﺮاي آزﻣﺎﯾﺶ ﻫﺎي ﻣﺮﺑﻮﻃﻪ، ﻣﺠﻤﻮﻋﻪ اي از اﻧﻮاع ﻣﺨﺘﻠﻒ ﺗﺼﺎوﯾﺮ ﺛﺎﺑﺖ و ﻫﻤﭽﻨﯿﻦ ﺗﺼﺎوﯾﺮ متحرک درﯾﺎﻓﺖ ﺷﺪه ﺗﻮﺳﻂ ﯾﮏ دورﺑﯿﻦ ﻣﻮرد اﺳﺘﻔﺎده ﻗﺮار ﮔﺮﻓﺘﻪ اﺳﺖ. تصاویر ﺑﺎ ﻧﺮخ 15 ﻓﺮﯾﻢ در ثانیه درﯾﺎﻓﺖ، ﭘﺮدازش و ﺑﺎ ﭘﺮوﺗﮑﻞ ﻣﻌﺮﻓﯽ ﺷﺪه و ﮐﺪﯾﻨﮓ ﻣﻨﭽﺴﺘﺮ ﺑﻪ ﭘﺮوﺗﺰ ﺑﯿﻨﺎﯾﯽ ارﺳﺎل ﻣﯽ ﺷﻮﻧﺪ.

ﮐﻠﻤﺎت ﮐﻠﯿﺪي: ﭘﺮوﺗﺰ ﺑﯿﻨﺎﯾﯽ، ﭘﺮدازش ﺗﺼﻮﯾﺮ، ﻓﯿﻠﺘﺮ ﮔﺎﺑﻮر، ﺗﺒﺪﯾﻞ ﮐﺴﯿﻨﻮﺳﯽ ﮔﺴﺴﺘﻪ، MINI2440

فایل PDF – در 20 صفحه- نویسنده : علی شاکر

طراحی بخش دریافت و پردازش تصویر برای یک پروتز بینایی

پسورد فایل : behsanandish.com

مجموعه مقالات فیلتر گابور (Gabor Filter) قسمت 1
مجموعه مقالات فیلتر گابور (Gabor Filter) قسمت 2

دسامبر 18, 2019/0 دیدگاه /توسط hgadmin

مجموعه مقالات فیلتر گابور (Gabor Filter) قسمت 1

آموزش عمومی پردازش تصویر و بینایی ماشین

1.A GABOR FILTER TEXTURE ANALYSIS APPROACH FOR HISTOPATHOLOGICAL BRAIN TUMOUR SUBTYPE DISCRIMINATION

Abstract Meningioma brain tumour discrimination is challenging as many histological patterns are mixed between the different subtypes. In clinical practice, dominant patterns are investigated for signs of specific meningioma pathology; however the simple observation could result in inter- and intra-observer variation due to the complexity of the histopathological patterns. Also employing a computerised feature extraction approach applied at a single resolution scale might not suffice in accurately delineating the mixture of histopathological patterns. In this work we propose a novel multiresolution feature extraction approach for characterising the textural properties of the different pathological patterns (i.e. mainly cell nuclei shape, orientation and spatial arrangement within the cytoplasm). The patterns’ textural properties are characterised at various scales and orientations for an improved separability between the different extracted features. The Gabor filter energy output of each magnitude response was combined with four other fixed-resolution texture signatures (2 model-based and 2 statistical-based) with and without cell nuclei segmentation. The highest classification accuracy of 95% was reported when combining the Gabor filters’ energy and the meningioma subimage fractal signature as a feature vector without performing any prior cell nuceli segmentation. This indicates that characterising the cell-nuclei self-similarity properties via Gabor filters can assists in achieving an improved meningioma subtype classification, which can assist in overcoming variations in reported diagnosis.

Keywords – texture analysis, Gabor filter, fractal dimension, meningioma histopathology, brain tumours

فایل PDF – در 14 صفحه- نویسنده : Omar Sultan Al-Kadi

A GABOR FILTER TEXTURE ANALYSIS APPROACH FOR HISTOPATHOLOGICAL BRAIN TUMOUR SUBTYPE DISCRIMINATION

پسورد فایل : behsanandish.com

2.A Review Paper on Gabor Filter Algorithm & Its Applications

Abstract— In applications of image analysis and computer vision, Gabor filters have maintained their popularity in feature extraction. The reason behind this is that the resemblance between Gabor filter and receptive field of simple cells in visual cortex. Being successful in applications like face detection, iris recognition, fingerprint matching; where, Gabor feature based processes are amongst the best performers. The Gabor features can be derived by applying signal processing techniques both in time and frequency domain. The models like human preattentive texture perception have been proposed which involves steps like convolution, inhibition and texture boundary detection. Texture features are based on the local power spectrum obtained by a bank of Gabor filters. The concept of sparseness to generate novel contextual multiresolution texture descriptors are described. In this paper we present the detailed study about the Gabor filter and its application.

Index Terms— Gabor filter, Gabor energy, image quality assessment, Gabor features, multiresolution techniques, segmentation, textured images..

فایل PDF – در 5 صفحه- نویسنده : Neelu Arora , Mrs. G. Sarvani

A Review Paper on Gabor Filter Algorithm & Its Applications

پسورد فایل : behsanandish.com

3.Comparison of texture features based on Gabor filters

Abstract -The performance of a number of texture feature operators is evaluated. The features are all based on the local spectrum which is obtained by a bank of Gabor ﬁlters. The comparison is made using a quantitative method which is based on Fisher’s criterion. It is shown that, in general, the discrimination effectiveness of the features increases with the amount of post-Gabor processing.

فایل PDF – در 6 صفحه- نویسنده : P. Kruizinga, N. Petkov and S.E. Grigorescu

Comparison of texture features based on Gabor filters

پسورد فایل : behsanandish.com

4.Evolutionary Gabor Filter Optimization with Application to Vehicle Detection

Abstract—Despite the considerable amount of research work on the application of Gabor ﬁlters in pattern classiﬁcation, their design and selection have been mostly done on a trial and error basis. Existing techniques are either only suitable for a small number of ﬁlters or less problem-oriented. A systematic and general evolutionary Gabor ﬁlter optimization (EGFO) approach that yields a more optimal, problem-speciﬁc, set of ﬁlters is proposed in this study. The EGFO approach uniﬁes ﬁlter design with ﬁlter selection by integrating Genetic Algorithms (GAs) with an incremental clustering approach. Speciﬁcally, ﬁlter design is performed using GAs, a global optimization approach that encodes the parameters of the Gabor ﬁlters in a chromosome and uses genetic operators to optimize them. Filter selection is performed by grouping together ﬁlters having similar characteristics (i.e., similar parameters) using incremental clustering in the parameter space. Each group of ﬁlters is represented by a single ﬁlter whose parameters correspond to the average parameters of the ﬁlters in the group. This step eliminates redundant ﬁlters, leading to a compact, optimized set of ﬁlters. The average ﬁlters are evaluated using an application-oriented ﬁtness criterion based on Support Vector Machines (SVMs). To demonstrate the effectiveness of the proposed framework, we have considered the challenging problem of vehicle detection from gray-scale images. Our experimental results illustrate that the set of Gabor ﬁlters, speciﬁcally optimized for the problem of vehicle detection, yield better performance than using traditional ﬁlter banks.

فایل PDF – در 8 صفحه- نویسنده : Zehang Sun, George Bebis and Ronald Miller

Evolutionary Gabor Filter Optimization with Application to Vehicle Detection

پسورد فایل : behsanandish.com

5.Expression-Invariant Face Recognition via 3D Face Reconstruction Using Gabor Filter Bank from a 2D Single Image

Abstract— In this paper, a novel method for expression- insensitive face recognition is proposed from only a 2D single image in a gallery including any facial expressions. A 3D Generic Elastic Model (3D GEM) is used to reconstruct a 3D model of each human face in the present database using only a single 2D frontal image with/without facial expressions. Then, the rigid parts of the face are extracted from both the texture and reconstructed depth based on 2D facial land-marks. Afterwards, the Gabor filter bank was applied to the extracted rigid-part of the face to extract the feature vectors from both texture and reconstructed depth images. Finally, by combining 2D and 3D feature vectors, the final feature vectors are generated and classified by the Support Vector Machine (SVM). Favorable outcomes were acquired to handle expression changes on the available image database based on the proposed method compared to several state-of-the-arts in expression-insensitive face recognition.

Keywords—Face recognition; 3D shape recovery; Gesture and Behavior Analysis.

فایل PDF – در 6 صفحه- نویسنده : Ali Moeini, Hossein Moeini, Karim Faez

Expression-Invariant Face Recognition via 3D Face Reconstruction Using Gabor Filter Bank from a 2D Single Image

پسورد فایل : behsanandish.com

6.IMAGE RETRIEVAL BASED ON HIERARCHICAL GABOR FILTERS

Content Based Image Retrieval (CBIR) is now a widely investigated issue that aims at allowing users of multimedia information systems to automatically retrieve images coherent with a sample image. A way to achieve this goal is the computation of image features such as the color, texture, shape, and position of objects within images, and the use of those features as query terms. We propose to use Gabor ﬁltration properties in order to ﬁnd such appropriate features. The article presents multichannel Gabor ﬁltering and a hierarchical image representation. Then a salient (characteristic) point detection algorithm is presented so that texture parameters are computed only in a neighborhood of salient points. We use Gabor texture features as image content descriptors and efﬁciently emply them to retrieve images.
Keywords: Gabor ﬁlters, image retrieval, texture feature extraction, hierarchical representation

فایل PDF – در 10 صفحه- نویسنده : TOMASZ ANDRYSIAK, MICHAŁ CHORA´ S

IMAGE RETRIEVAL BASED ON HIERARCHICAL GABOR FILTERS

پسورد فایل : behsanandish.com

7.Iris Recognition Based On Adaptive Gabor Filter

Abstract. Aiming at the problem of multi-category iris recognition, there proposes a method of iris recognition algorithm based on adaptive Gabor ﬁlter. Use DE-PSO to adaptive optimize the Gabor ﬁlter parameters. DE-PSO is composed of particle swarm optimization and differential evolution algorithm. Use 16 groups of 2D-Gabor ﬁlters with different frequencies and directions to process iris images. According to the direction and frequency of maximum response amplitude, transform iris features into 512-bit binary feature encoding. Calculate the Hamming distance of feature code and compare with the classiﬁcation threshold, determine iris the type of iris. Experiment on a variety of iris databases with multiple Gabor ﬁlter algorithms, the results showed that this algorithm has higher recognition rate, the ROC curve is closer to the coordinate axis and the robustness is better, compare with other Gabor ﬁlter algorithm.

Keywords: Iris recognition Gabor ﬁlter Particle swarm optimization Differential evolutionFeature encodingHamming distance

فایل PDF – در 8 صفحه- نویسنده : Shuai Liu, Yuanning Liu, Xiaodong Zhu, Guang Huo, Jingwei Cui, and Yihao Chen

Iris Recognition Based On Adaptive Gabor Filter

پسورد فایل : behsanandish.com

8.USE OF GABOR FILTERS FOR TEXTURE CLASSIFICATION OF AIRBORNE IMAGES AND LIDAR DATA

KEY WORDS: Texture analysis, LIDAR, Algorithm, Urban and Vegetation Detection, Automated Classification

ABSTRACT: In this paper, a texture approach is presented for building and vegetation extraction from LIDAR and aerial images. The texture is very important attribute in many image analysis or computer vision applications. The procedures developed for texture problem can be subdivided into four categories: structural approach, statistical approach, model based approach and filter based approach. In this paper, different definitions of texture are described, but complete emphasis is given on filter based methods. Examples of filtering methods are Fourier transform, Gabor and wavelet transforms. Here, Gabor filter is studied and its implementation for texture analysis is explored. This approach is inspired by a multi-channel filtering theory for processing visual information in the human visual system. This theory holds that visual system decomposes the image into a number of filtered images of a specified frequency, amplitude and orientation. The main objective of the article is to use Gabor filters for automatic urban object and tree detection. The first step is a definition of Gabor filter parameters: frequency, standard deviation and orientation. By varying these parameters, a filter bank is obtained that covers the frequency domain almost completely. These filters are used to aerial images and LIDAR data. The filtered images that possess a significant information about analyzed objects are selected, and the rest are discarded. Then, an energy measure is defined on the filtered images in order to compute different texture features. The Gabor features are used to image segmentation using thresholding. The tests were performed using set of images containing very different landscapes: urban area and vegetation of varying configurations, sizes and shapes of objects. The performed studies revealed that textural algorithms have the ability to detect buildings and trees. This article is the attempt to use texture methods also to LIDAR data, resampling into regular grid cells. The obtained preliminary results are interesting.

فایل PDF – در 12 صفحه- نویسنده : Urszula Marmol

USE OF GABOR FILTERS FOR TEXTURE CLASSIFICATION OF AIRBORNE IMAGES AND LIDAR DATA

پسورد فایل : behsanandish.com

دسامبر 17, 2019/0 دیدگاه /توسط daliri

ماشین بردار پشتیبان (svm) قسمت 3

آموزش عمومی پردازش تصویر و بینایی ماشین

تاريخچه

الگوريتم SVM اوليه در ۱۹۶۳ توسط Vladimir Vapnik ابداع شد و در سال ۱۹۹۵ توسطVapnik و Corinna Cortes براي حالت غيرخطي تعميم داده شد.

ماشين بردار پشتيباني (Support vector machines) يکي از روش‌هاي يادگيري بانظارت(Supervised learning) است که از آن براي طبقه‌بندي و رگرسيون استفاده مي‌کنند.

اين روش از جمله روش‌هاي نسبتاً جديدي است که در سال‌هاي اخير کارايي خوبي نسبت به روش‌هاي قديمي‌تر براي طبقه‌بندي از جمله شبکه‌هاي عصبي پرسپترون نشان داده است. مبناي کاري دسته‌بنديکنندة SVM دسته‌بندي خطي داده‌ها است و در تقسيم خطي داده‌ها سعي مي‌کنيم خطي را انتخاب کنيم که حاشيه اطمينان بيشتري داشته باشد. حل معادلة پيدا کردن خط بهينه براي داده‌ها به وسيله روش‌هايQP (Quadratic Programming) که روش‌هاي شناخته شده‌اي در حل مسائل محدوديت‌دار هستند صورت مي‌گيرد.

SVM از يک تکنيک که kernel trick ناميده مي شود، براي تبديل داده هاي شما استفاده مي کند و سپس بر اساس اين تبديل، مرز بهينه بين خروجي هاي ممکن را پيدا مي کند. به عبارت ساده تبديلات بسيار پيچيده را انجام مي دهد، سپس مشخص مي کند چگونه داده هايتان را بر اساس برچسب ها يا خروجي هايي که تعريف کرده ايد، جدا کنيد.

يکي از روش هايي که در حال حاضر به صورت گسترده براي مسئله دسته بندي (Classification) مورد استفاده قرار مي گيرد، روش ماشين بردار پشتيبان (SVM) است. شايد به گونه اي بتوان محبوبيت کنوني روش ماشين بردار پشتيبان را با محبوبيت شبکه هاي عصبي در دهه گذشته مقايسه کرد. علت اين قضيه نيز قابليت استفاده اين روش در حل مسائل گوناگون مي باشد، در حاليکه روش هايي مانند درخت تصميم گيري را نمي توان به راحتي در مسائل مختلف به کار برد.

کاربردهاي SVM

الگوريتم SVM، جز الگوريتم هاي تشخيص الگو دسته بندي مي شود. از الگوريتم SVM، در هر جايي که نياز به تشخيص الگو يا دسته بندي اشيا در کلاس هاي خاص باشد مي توان استفاده کرد. در ادامه به کاربرد هاي اين الگوريتم به صورت موردي اشاره مي شود:

سيستم آناليز ريسک، کنترل هواپيما بدون خلبان، رديابي انحراف هواپيما، شبيه سازي مسير، سيستم راهنمايي اتوماتيک اتومبيل، سيستمهاي بازرسي کيفيت، آناليز کيفيت جوشکاري، پيش بيني کيفيت، آناليز کيفيت کامپيوتر، آناليز عملياتهاي آسياب، آناليز طراحي محصول شيميايي، آناليز نگهداري ماشين، پيشنهاد پروژه، مديريت و برنامه ريزي، کنترل سيستم فرايند شيميايي و ديناميکي، طراحي اعضاي مصنوعي، بهينه سازي زمان پيوند اعضا، کاهش هزينه بيمارستان، بهبود کيفيت بيمارستان، آزمايش اتاق اورژانس، اکتشاف روغن و گاز، کنترل مسير در دستگاههاي خودکار، ربات، جراثقال، سيستمهاي بصري، تشخيص صدا، اختصار سخن، کلاسه بندي صوتي، آناليز بازار، سيستمهاي مشاوره اي محاسبه هزينه موجودي، اختصار اطلاعات و تصاوير، خدمات اطلاعاتي اتوماتيک، مترجم لحظه اي زبان، سيستمهاي پردازش وجه مشتري، سيستمهاي تشخيص ترمز کاميون، زمانبندي وسيله نقليه، سيستمهاي مسيريابي، کلاسه بندي نمودارهاي مشتري/بازار، تشخيص دارو، بازبيني امضا، تخمين ريسک وام، شناسايي طيفي، ارزيابي سرمايه، کلاسه بندي انواع سلولها، ميکروبها و نمونه ها، پيش بيني فروشهاي آينده، پيش بيني نيازهاي محصول، پيش بيني وضعيت بازار، پيش بيني شاخصهاي اقتصادي، پيش بيني ملزومات انرژي، پيش بيني واکنشهاي دارويي، پيش بيني بازتاب محصولات شيميايي، پيش بيني هوا، پيش بيني محصول، پيش بيني ريسک محيطي، پيش بيني جداول داوري، مدل کردن کنترل فرآيند، آناليز فعاليت گارانتي، بازرسي اسناد، تشخيص هدف، تشخيص چهره، انواع جديد سنسورها، دستگاه کاشف زير دريايي بوسيله امواج صوتي، رادار، پردازش سيگنالهاي تصويري شامل مقايسه اطلاعات، پيگيري هدف، هدايت جنگ افزارها، تعيين قيمت وضعيت فعلي، جلوگيري از پارازيت، شناسايي تصوير /سيگنال، چيدمان يک مدار کامل، بينايي ماشين، مدل کردن غير خطي، ترکيب صدا، کنترل فرآيند ساخت، آناليز مالي، پيش بيني فرآيندهاي توليد، ارزيابي بکارگيري يک سياست، بهينه سازي محصول، تشخيص ماشين و فرآيند، مدل کردن کنترل سيستمها، مدل کردن ساختارهاي شيميايي، مدل کردن سيستمهاي ديناميکي، مدل کردن سيگنال تراکم، مدل کردن قالبسازي پلاستيکي، مديريت قراردادهاي سهام، مديريت وجوه بيمه، ديريت سهام، تصويب چک بانکي، اکتشاف تقلب در کارت اعتباري، ثبت نسيه، بازبيني امضا از چکها، پيش بيني ارزش نسيه، مديريت ريسک رهن، تشخيص حروف و اعدا، تشخيص بيماري و…..

ايده اصلي SVM

l با فرض اينکه دسته ها بصورت خطي جداپذير باشند، ابرصفحه هائي با حداکثر حاشيه(maximum margin) را بدست مي آورد که دسته ها را جدا کنند.

l در مسايلي که داده ها بصورت خطي جداپذير نباشند، داده ها به فضاي با ابعاد بيشتر نگاشت پيدا مي کنند تا بتوان آنها را در اين فضاي جديد بصورت خطي جدا نمود.

l در يک فرايند يادگيري که شامل دو کلاس ميباشد، هدف SVM پيدا کردن بهترين تابع براي طبقهبندي ميباشد به نحوي که بتوان اعضاي دو کلاس را در مجموعه دادهها از هم تشخيص داد. معيار بهترين طبقهبندي بهصورت هندسي مشخص ميشود، براي مجموعه دادههايي که بهصورت خطي قابل تجزيه هستند. بهطور حسي آن مرزي که بهصورت بخشي از فضا تعريف ميشود يا همان تفکيک بين دو کلاس بوسيله hyperplane تعريف ميشود. همين تعريف هندسي به ما اجازه ميدهد تا کشف کنيم که چگونه مرزها را بيشينه کنيم ولو اينکه تعداد بيشماري hyperplane داشته باشيم و فقط تعداد کمي، شايستگي راه حل براي SVM دارند.

مسئله جداسازي خطي: Linear Discrimination

اگر دو دسته وجود داشته باشند که بصورت خطي از هم جداپذير باشند، بهترين جدا کننده اين دو دسته چيست؟

الگوريتم هاي مختلفي از جمله پرسپترون ميتوانند اين جداسازي را انجام دهند.

آيا همه اين الگوريتمها بخوبي از عهده اين کار بر مي آيند؟

آشنايي با مفاهيم ابتدايي

خط يا ابر صفحه جدا کننده:

هدف: پيدا کردن بهترين خط ( ابر صفحه) که دو دسته را از هم جدا کند. در حالت دو بعدي معادله اين خط بصورت زير است:

در حالت n بعدي خواهيم داشت:

حداکثر حاشيه (maximum margin)

بر طبق قضيه اي در تئوري يادگيري اگر مثالهاي آموزشي بدرستي دسته بندي شده باشند، از بين جداسازهاي خطي، آن جداسازي که حاشيه داده هاي آموزشي را حداکثر مي کند، خطاي تعميم را حداقل خواهد کرد.

چرا حداکثر حاشيه؟

¢ به نظر مي رسد که مطمئن ترين راه باشد.

¢ تئوري هائي برمبناي VC dimension وجود دارد که مفيد بودن آنرا اثبات مي کند.

¢ بطور تجربي اين روش خيلي خوب جواب داده است.

¢ دليل اينکه SVM روي بزرگترين مرز براي hyperplane پافشاري ميکند اينست که قضيه قابليت عموميت بخشيدن به الگوريتم را بهتر تامين ميکند. اين نه تنها به کارايي طبقهبندي و دقت آن روي دادههاي آزمايشي کمک ميکند، فضا را نيز براي طبقهبندي بهتر دادههاي آتي مهيا ميکند.

بردار پشتيبان

نزديکترين داده هاي آموزشي به ابر صفحه هاي جدا کننده بردار پشتيبان ناميده مي شوند.

ماشين بردار پشتيبان خطي

ماشين بردار پشتيبان يک روش يادگيري نسبتا جديد است که اغلب براي کلاسبندي باينري مورد استفاده واقع مي شود. فرض کنيد L مشاهده داريم که هر مشاهده مشتمل بر زوج هاي است که در آن . بردار ورودي و يک مقدار دو وضعيتي (1- يا 1+) است. ايده ي ماشين بردار پشتيبان مي کوشد، ابرصفحاتي در فضا رسم کند که عمل تمايز نمونه هاي کلاس هاي مختلف داده ها را بطور بهينه انجام دهد. مي توان يک ابرصفحه را از طريق رابطه زير نشان داد:

براي يک بردار خطي b با وزن w ، حاشيه جداسازي عبارتست از فاصله ي بين ابرصفحه تعريف شده توسط رابطه ي فوق و نزديکترين ويژگي به آن. هدف ماشين بردار پشتيبان يافتن ابرصفحه اي ست که بيشترين حاشيه ي جداسازي را داشته باشد. مهمترين وظيفه SVM ، يافتن پارامترهاي w0 و b0 بر اساس بردارهاي آموزشي داده شده، براي اين ابرصفحه بهينه است. براي يک بردار ويژگي X، فاصله تا ابرصفحه بهينه به صورت زير است:

از رابطه بالا نتيجه مي شود که ماکزيموم کردن حاشيه جداسازي بين الگوها و ابرصفحه، معادلست با مينيموم کردن فرم اقليدسي بردار وزن w. بنابراين مساله بهينه سازي مقيد را مي توان به صورت زير تعريف کرد:

براي حل اين مساله، تابع لاگرانژ زير را تشکيل داده و حل مي کنيم:

لاگرانژين L بايد نسبت به متغيرهاي اوليه bو w مينيموم و نسبت به متغيرهاي دوگان ماکزيموم شود. با مساوي صفر قراردادن مشتق L نسبت به b،w:

به معادلات زير خواهيم رسيد:

مجموعه جواب، بسطي از نمونه هاي آموزشي است که مقدار متناظر با آن ها، يک مقدار غير صفر است. اين نمونه هاي آموزشي خاص به بردارهاي پشتيبان مشهورند. بردارهاي پشتيبان روي مرز حاشيه قرار دارند. مابقي نمونه هاي آموزشي در اين قسمت نقشي ندارند.

تمايز نمونه هاي دو کلاس با ابرصفحه ي بهينه

با قرار دادن 7 و 8 در به مساله دوگان ولف زير خواهيم رسيد:

حل اين مساله دوگان ضرايب لاگرانژ را به ما مي دهد. تابع ابرصفحه متمايز کننده را مي توان به صورت زير نوشت:

ماشين بردار پشتيبان براي بردارهاي ورودي جدايي ناپذير:

اغلب در عمل، يافتن يک ابرصفحه متمايز کننده به راحتي امکان پذير نيست. زيرا مثلا يک نويز قوي مي تواند باعث ايجاد رويهم افتادگي کلاس ها شود. در اين حالت از متغير هايي به نام متغيرهاي کمبود(Slack Variables) استفاده مي کنيم. به گونه اي که شرايط زير برقرار باشند:

حال يک تعميم خوب براي ابرصفحه ي متمايز کننده، با کنترل ظرفيت کلاسبند (از طريق ) و همچنين تعداد خطاهاي مرحله آموزش بدست مي آيد. مساله بهينه سازي به صورت زير تعريف خواهد شد:

مساله دوگان به فرم زير خواهد بود:

ماشين بردار پشتيبان غيرخطي:

ابرصفحه جداکننده بهينه اولين بار توسط Vapnik در سال ۱۹۶۳ ارائه شد که يک دسته کننده خطي بود. در سال ۱۹۹۲ ،Bernhard Boser ، Isabelle GuyonوVapnik راهي را براي ايجاد دسته بند غيرخطي، با استفاده قرار دادن هسته براي پيدا کردن ابرصفحه با بيشتر حاشيه، پيشنهاد دادند. الگوريتم نتيجه شده ظاهرا مشابه است، به جز آنکه تمام ضرب هاي نقطه اي با يک تابع هسته غيرخطي جايگزين شده اند. اين اجازه مي دهد، الگوريتم، براي ابرصفحه با بيشترين حاشيه در يک فضاي ويژگيِ تغييرشکل داده، مناسب باشد. ممکن است، تغييرشکل غيرخطي باشد و فضاي تغيير يافته، داراي ابعاد بالاتري باشد. به هر حال دسته کننده، يک ابرصفحه در فضاي ويژگي با ابعاد بالا است، که ممکن است در فضاي ورودي نيز غيرخطي باشد.

در حالت غيرخطي، مي توان با اعمال پيش پردازش داده ها، مساله را به فضايي برد که در آن جا با يک ابرصفحه ساده قابل حل باشد. براي اين منظور يک نگاشت تعريف مي کنيم که بردار ورودي d بعدي x را به بردار d’ بعدي z تبديل مي کند.

بايد به گونه اي انتخاب شود که بردارهاي فضاي ويژگي جديد جدايي پذير باشند. در حالت کلي مي توان گفت که اگر بردارهاي ورودي را به فضايي ببرد که تعداد ابعاد آن به اندازه کافي بزرگ باشد (

منبع

منابع

1.https://fa.wikipedia.org

2.http://www.bigdata.ir

3.www.barjoueian.com

4.http://fumblog.um.ac.ir

ماشین بردار پشتیبان (svm) قسمت 1
ماشین بردار پشتیبان (svm) قسمت 2
ماشین بردار پشتیبان (svm) قسمت 3

دسامبر 16, 2019/0 دیدگاه /توسط hgadmin

ماشین بردار پشتیبان (svm) قسمت 2

آموزش عمومی پردازش تصویر و بینایی ماشین

یادگیری ماشین – SVM یا ماشین بردار پشتیبان به زبان ساده

سید مجتبی بنائی ۱۳۹۴/۰۵/۱۶ مفاهیم پایه نظرات 31,220 مشاهده

یکی از الگوریتم ها و روشهای بسیار رایج در حوزه دسته بندی داده ها، الگوریتم SVM یا ماشین بردار پشتیبان است که در این مقاله سعی شده است به زبان ساده و به دور از پیچیدگیهای فنی توضیح داده شود.

آشنایی با مفهوم دسته بندی

فرض کنید مجموعه داده ای داریم که ۵۰٪ افراد آن مرد و ۵۰٪ افراد آن زن هستند. این مجموعه داده می تواند مشتریان یک فروشگاه آنلاین باشد. با داشتن یک زیرمجموعه از این داده ها که جنسیت افراد در آن مشخص شده است، می خواهیم قوانینی ایجاد کنیم که به کمک آنها جنسیت بقیه افراد مجموعه را بتوانیم با دقت بالایی تعیین کنیم. تشخیص جنسیت بازدیدکنندگان فروشگاه، باعث می شود بتوانیم تبلیغات جداگانه ای را برای زنان و مردان نمایش دهیم و سودآوری فروشگاه را بالا ببریم . این فرآیند را در علم تحلیل داده، دسته بندی می نامیم .

برای توضیح کامل مسأله، فرض کنید دو پارامتری که قرار است جنسیت را از روی آنها تعیین کنیم، قد و طول موی افراد است . نمودار پراکنش قد و طول افراد در زیر نمایش داده شده است که در آن جنسیت افراد با دو نماد مربع (مرد) و دایره (زن) به طور جداگانه نمایش داده شده است .

SVM-1

با نگاه به نمودار فوق، حقایق زیر به سادگی قابل مشاهده است :

مردان در این مجموعه، میانگین قد بلندتری دارند.
زنان از میانگین طول موی بیشتری برخوردار هستند.

اگر یک داده جدید با قد ۱۸۰cm و طول موی ۴cm به ما داده شود، بهترین حدس ما برای ماشینی این شخص، دسته مردان خواهد بود .

بردارهای پشتیبان و ماشین بردار پشتیبان

بردارهای پشتیبان به زبان ساده، مجموعه ای از نقاط در فضای n بعدی داده ها هستند که مرز دسته ها را مشخص می کنند و مرزبندی و دسته بندی داده ها براساس آنها انجام می شود و با جابجایی یکی از آنها، خروجی دسته بندی ممکن است تغییر کند . به عنوان مثال در شکل فوق ، بردار (۴۵,۱۵۰) عضوی از بردار پشتیبان و متعلق به یک زن است . در فضای دوبعدی ،‌بردارهای پشتیبان، یک خط، در فضای سه بعدی یک صفحه و در فضای n بعدی یک ابر صفحه را شکل خواهند داد.

SVM یا ماشین بردار پشتیبان ، یک دسته بند یا مرزی است که با معیار قرار دادن بردارهای پشتیبان ، بهترین دسته بندی و تفکیک بین داده ها را برای ما مشخص می کند.

در SVM فقط داده های قرار گرفته در بردارهای پشتیبان مبنای یادگیری ماشین و ساخت مدل قرار می گیرند و این الگوریتم به سایر نقاط داده حساس نیست و هدف آن هم یافتن بهترین مرز در بین داده هاست به گونه ای که بیشترین فاصله ممکن را از تمام دسته ها (بردارهای پشتیبان آنها) داشته باشد .

چگونه یک ماشین بر مبنای بردارهای پشتیبان ایجاد کنیم ؟

به ازای داده های موجود در مثال فوق، تعداد زیادی مرزبندی می توانیم داشته باشیم که سه تا از این مرزبندی ها در زیر نمایش داده شده است.

SVM-2

سوال اینجاست که بهترین مرزبندی در این مسأله کدام خط است ؟

یک راه ساده برای انجام اینکار و ساخت یک دسته بند بهینه ، محاسبه فاصله ی مرزهای به دست آمده با بردارهای پشتیبان هر دسته (مرزی ترین نقاط هر دسته یا کلاس) و در نهایت انتخاب مرزیست که از دسته های موجود، مجموعاً بیشترین فاصله را داشته باشد که در شکل فوق خط میانی ، تقریب خوبی از این مرز است که از هر دو دسته فاصله ی زیادی دارد. این عمل تعیین مرز و انتخاب خط بهینه (در حالت کلی ، ابر صفحه مرزی) به راحتی با انجام محاسبات ریاضی نه چندان پیچیده قابل پیاده سازی است .

توزیع غیر خطی داده ها و کاربرد ماشین بردار پشتیبان

اگر داده ها به صورت خطی قابل تفکیک باشند، الگوریتم فوق می تواند بهترین ماشین را برای تفکیک داده ها و تعیین دسته یک رکورد داده، ایجاد کند اما اگر داده ها به صورت خطی توزیع شده باشند (مانند شکل زیر )، SVM را چگونه تعیین کنیم ؟

SVM-3

در این حالت، ما نیاز داریم داده ها را به کمک یک تابع ریاضی (Kernel functions) به یک فضای دیگر ببریم (نگاشت کنیم ) که در آن فضا، داده ها تفکیک پذیر باشند و بتوان SVM آنها را به راحتی تعیین کرد. تعیین درست این تابع نگاشت در عملکرد ماشین بردار پشتیبان موثر است که در ادامه به صورت مختصر به آن اشاره شده است.

با فرض یافتن تابع تبدیل برای مثال فوق،‌ فضای داده ما به این حالت تبدیل خواهد شد :

SVM-4

در این فضای تبدیل شده، یافتن یک SVM به راحتی امکان پذیر است .

نگاهی دقیق تر به فرآیند ساخت SVM

همانطور که اشاره شد،‌ماشین بردار پشتیبان یا SVM داده ها را با توجه به دسته های از پیش تعیین شده آنها به یک فضای جدید می برد به گونه ای که داده ها به صورت خطی (یا ابر صفحه ) قابل تفکیک و دسته بندی باشند و سپس با یافتن خطوط پشتیبان (صفحات پشتیبان در فضای چند بعدی) ، سعی در یافتن معادله خطی دارد که بیشترین فاصله را بین دو دسته ایجاد می کند.

در شکل زیر داده ها در دو دوسته آبی و قرمز نمایش داده شده اند و خطوط نقطه چین ، بردار های پشتیبان متناظر با هر دسته را نمایش می دهند که با دایره های دوخط مشخص شده اند و خط سیاه ممتد نیز همان SVM است . بردار های پشتیبان هم هر کدام یک فرمول مشخصه دارند که خط مرزی هر دسته را توصیف می کند.

SVM‌ در پایتون

برای استفاده از ماشین بردار پشتیبان در پایتون، توصیه بنده استفاده از کتابخانه یادگیری ماشین پایتون به نام scikit–learn است که تمام کرنل ها و توابع نگاشت را به صورت آماده شده دارد. سه تا تابعSVC , NuSVC , LinearSVC وظیفه اصلی دسته بندی را برعهده دارند . (SVC = Support Vector Classifier) . نمونه ای از دسته بندی با این توابع را در زیر می توانید مشاهده کنید :

ماشین بردار پشتیبانی در عمل

برای استفاده از SVM در مورد داده های واقعی ، چندین نکته را باید رعایت کنید تا نتایج قابل قبولی را بگیرید

ابتدا داده ها را پالایش کنید (نقاط پرت ،‌ داده های ناموجود و …..)
داده را عددی و نرمال کنید . این مباحث را در مقالات پیش پردازش داده ها دنبال کنید. به طور خلاصه ، داده هایی مانند جنسیت، رشته تحصیلی و … را به عدد تبدیل کنید و سعی کنید مقادیر همه صفات بین یک تا منهای یک [۱,-۱] نرمال شوند تا بزرگ یا کوچک بودن مقادیر یک ویژگی داده ها،‌ ماشین را تحت تاثیر قرار ندهد .
کرنل های مختلف را امتحان و به ازای هر کدام، با توجه به مجموعه داده آموزشی که در اختیار دارید و دسته بندی داده های آنها مشخص است، دقت SVM را اندازه گیری کنید و در صورت نیاز پارامتر های توابع تبدیل را تغییر دهید تا جواب های بهتری بگیرید. این کار را برای کرنل های مختلف هم امتحان کنید . می توانید از کرنل RBF شروع کنید .

نقاط ضعف ماشین بردار پشتیان

این نوع الگوریتم ها، محدودیت های ذاتی دارند مثلا هنوز مشخص نشده است که به ازای یک تابع نگاشت ، پارامترها را چگونه باید تعیین کرد.
ماشینهای مبتنی بر بردار پشتیبان به محاسبات پیچیده و زمان بر نیاز دارند و به دلیل پیچیدگی محاسباتی، حافظه زیادی نیز مصرف می کنند.
داده های گسسته و غیر عددی هم با این روش سازگار نیستند و باید تبدیل شوند.

با این وجود، SVM‌ ها دارای یک شالوده نظری منسجم بوده و جواب های تولید شده توسط آنها ، سراسری و یکتا می باشد. امروزه ماشینهای بردار پشتیبان، به متداول ترین تکنیک های پیش بینی در داده کاوی تبدیل شده اند.

سخن پایانی

ماشینهای بردار پشتیبان، الگوریتم های بسیار قدرتمندی در دسته بندی و تفکیک داده ها هستند بخصوص زمانی که با سایر روشهای یادگیری ماشین مانند روش جنگل تصادفی تلفیق شوند. این روش برای جاهایی که با دقت بسیار بالا نیاز به ماشینی داده ها داریم، به شرط اینکه توابع نگاشت را به درستی انتخاب کنیم، بسیار خوب عمل می کند .

ساختار اصلی این نوشتار از روی یک مقاله سایت آنالیتیکزویدیا برداشته شده است و برای دو بخش پایانی مقاله هم از کتاب «داده کاوی پیشرفته : مفاهیم و الگوریتم ها» دکتر شهرابی استفاده شده است .

منبع

آشنایی با ماشین بردار پشتیبان (SVM) – مرور کلی

SVM دقیقا چه چیزی هست؟

SVM یک مدل یادگیری نظارت شده است.

پس قبل از این که به سراغ آن برویم باید یک مجموعه داده(Dataset) که از قبل برچسب‌گذاری شده(Labeled) را داشته باشیم.

مثال: فرض کنیم من صاحب یک کسب‌وکار هستم و هر روز تعداد زیادی ایمیل از مشتری‌ها دریافت می‌کنم. بعضی از این ایمیل‌ها شکایت‌ها و نارضایتی‌هایی هستند که من هرچه سریع‌تر باید به آن‌ها پاسخ بدهم و به آن‌ها رسیدگی کنم. در غیر این صورت کسب‌وکار من با ضرر روبرو خواهد شد.

من به دنبال راهی هستم که این ایمیل‌ها را هرچه سریع‌تر تشخیص بدهم(پیدا کنم) و پاسخ آن‌ها را زودتر از بقیه ارسال کنم.

رویکرد اول: من می‌توانم برچسب‌هایی با عنوان‌های: اورژانسی، شکایت و راهنمایی در جیمیل(GMail) خود ایجاد کنم.

اشکال این روش این است که من باید مدتی فکر کنم و همه کلمه‌های کلیدی(Keyword) بالغوه که مشتری‌های عصبانی ممکن است در ایمیل‌های خود استفاده کنند را پیدا کنم. طبیعی است که بعضی از آن‌ها را هم از قلم انداخته شوند. با گذشت زمان هم لیست این کلمه‌ها به احتمال زیاد شلوغ و مدیریت کردن آن‌ها به کار مشکلی تبدیل می‌شود.

رویکرد دوم: من می‌توانم از یک الگوریتم یادگیری ماشین نظارت شده استفاده کنم.

قدم اول: به تعدادی ایمیل نیاز دارم.(هرچه بیشتر بهتر)

قدم دوم: عنوان ایمیل‌های قدم اول رو می‌خوانم و آن‌ها را در یکی از دو گروه «شکایت است» و یا «شکایت نیست» طبقه‌بندی می‌کنم. اینجوری می‌توانم ایمیل‌ها را برچسب ‌گذاری کنم.

قدم سوم: روی این مجموعه داده، مدلی را آموزش می‌دهم.

قدم چهارم: کیفیت یا صحت پیش‌بینی های مدل آموزش داده‌شده را ارزیابی می‌کنم.(با استفاده از روش Cross Validation)

قدم پنجم: از این مدل برای پیش‌بینی این که ایمیل‌های جدیدی که رسیده‌اند، شکایت هستند یا نه، استفاده می‌کنم.

در این رویکرد اگر مدل را با تعداد ایمیل‌های زیادی آموزش داده باشیم، مدل عملکرد خوبی را نشون می‌دهد. SVM فقط یکی از روش‌هایی هست که ما می‌توانیم برای یادگرفتن از داده‌های موجود و پیش‌بینی کردن، استفاده کنیم.

همچنین باید به این نکته هم توجه داشته باشیم که قدم دوم اهمیت زیادی دارد و دلیلش این است که اگر در شروع کار، ایمیل‌های برچسب‌گذاری نشده را به SVM بدهیم، کار خاصی را نمیتواند انجام دهد.

SVM یک مدل خطی را یاد می‌گیرد

در مثال قبل دیدیم که در قدم سوم یک الگوریتم یادگیری نظارت شده مثل SVM به کمک داده‌هایی که از قبل برچسب‌گذاری شده‌اند آموزشداده شد. اما برای چه چیزی آموزش داده شد؟ برای این که چیزی را یاد بگیرد.

چه چیزی را یاد بگیرد؟

در مورد SVM، یک مدل خطیرا یاد میگیرد.

مدل خطی چیست؟ اگر بخواهیم به زبان ساده بیان کنیم یک خط است.(و در حالت پیچیده‌تر یک ابر صفحه).

اگر داده‌های شما خیلی ساده و دو بعدی باشند، در این صورت SVM خطی را یاد می‌گیرد که آن خط می‌تواند داده‌ها را به دو بخش تقسیم کند.

svm

SVM قادر است که خطی را پیدا کند که داده‌ها را جدا می‌کند.

خب پس اگر SVM فقط یک خط است، پس چرا ما داریم راجع به مدل خطی صحبت می‌کنیم؟

برای این که ما همینطوری نمی‌توانیم به یک خط چیزی را آموزش بدهیم.

در عوض:

در نظر می‌گیریم که داده‌هایی که می‌خواهیم طبقه‌بندی کنیم، می‌توانند به وسیله یک خط از هم تفکیک شوند.
می‌دانیم که یک خط می‌تواند به کمک معادله y=wx+by=wx+b نمایش داده شود.(این همان مدل ما است)
می‌دانیم با تغییر دادن مقدار w و b بی‌نهایت خط وجود خواهد داشت.
برای تعیین این که کدام مقدار w و b بهترینخط جداکننده داده‌ها را به ما می‌دهد، از یک الگوریتم استفاده می‌کنیم.

SVM یکی از این الگوریتم‌ها هست که می‌تواند این کار را انجام دهد.

الگوریتم یا مدل؟

در شروع این پست من نوشتم که SVM یک مدل یادگیری نظارت شده است، و الآن می‌نویسم که آن یک الگوریتم است. چه شده؟ از واژه الگوریتم معمولا آزادانه استفاده می‌شود. برای نمونه، ممکن است که شما جایی بخوانید یا بشنوید که SVM یک الگوریتم یادگیری نظارت شده است. اگر این نکته را در نظر بگیریم که الگوریتم مجموعه‌ای از فعالیت‌ها است که انجام می‌شوند تا به نتیجه مشخصی دست یابیم، می‌بینیم که استفاده از این واژه در اینجا صحیح نیست(منظور از واژه الگوریتم اینجا الگوریتمی است که برای آموزش از آن استفاده می‌کنیم). بهینه‌سازی متوالی کمینه(Sequential minimal optimization) پر استفاده ترین الگوریتم برای آموزش SVM است. با این حال می‌توان از الگوریتم‌های دیگری مثل کاهش مختصات(Coordinate descent) هم استفاده کرد. در کل بیشتر به جزییاتی مثل این علاقمند نیستند، در نتیجه ما هم برای ساده‌تر شدن فقط از واژه الگوریتم SVM استفاده می‌کنیم(بدون ذکر جزییات الگوریتم آموزشی که استفاده می‌کنیم).

SVM یا SVMها؟

بعضی وقت‌ها می‌بینیم که مردم راجع به SVM و بعضی وقت‌ها هم راجع به SVMها صحبت می‌کنند.

طبق معمول ویکی‌پدیا در روشن و شفاف کردن چیزها به ما کمک می‌کند:

در یادگیری ماشینی، ماشین‌های بردار پشتیبان (SVMs) مدل‌های یادگیری نظارت شده به همراه الگوریتم‌های آموزش مربوطههستندکه در تحلیل داده‌های استفاده شده در رگرسیون و طبقه‌بندی از آن‌ها استفاده می‌شود.(ویکی‌پدیا)

پس حالا ما این را می‌دانیم که چندین مدل‌ متعلق به خانواده SVM وجود دارند.

SVMها – ماشین‌های بردار پشتیبان

بر اساس ویکی‌پدیا SVMها همچنین می‌توانند برای دو چیز استفاده شوند، طبقه‌بندی و رگرسیون.

SVM برای طبقه‌بندی استفاده می‌شود.
SVR یا(Support Vector Regression) برای رگرسیون.

پس گفتن ماشین‌های بردار پشتیبان هم دیگه الآن منطقی به نظر میاد. با این وجود این پایان داستان نیست!

طبقه‌بندی

در سال ۱۹۵۷ یک مدل خطی ساده به نام پرسپترون توسط فردی به نام فرانک روزنبلت برای طبقه‌بندی اختراع شد(که در واقع اساس شبکه‌های عصبی ساده‌ای به نام پرسپترون چند لایه است).

چند سال بعد، واپنیک و چروننکیس مدل دیگری به نام «طبقه‌بندی کننده حداکث حاشیه» پیشنهاد دادند و همان‌جا بود که SVM متولد شد.

در سال ۱۹۹۲ واپنیک و همکارانش ایده‌ای داشتند که یک چیزی به نام کلک کرنل(Kernel Trick) را به روش قبلی اضافه کنند تا به آن‌ها اجازه دهد که حتی داده‌هایی که به صورت خطی تفکیک‌پذیر نیستند را هم طبقه‌بندی کنند.

سرانجام در سال ۱۹۹۵، کورتز و واپنیک، طبقه‌بندی کننده حاشیه نرم را معرفی کردند که به SVM اجازه می‌دهد تا بعضی از اشتباهات در طبقه‌بندی را هم بپذیرد.

پس وقتی که ما از طبقه‌بندی صحبت می‌کنیم، چهار ماشین بردار پشتیبان مختلف وجود دارد.

طبقه‌بندی کننده حاشیه حداکثر.
نسخه‌ای که از کلک کرنل استفاده می‌کند.
نسخه‌ای که از حاشیه نرم استفاده می‌کند.
نسخه‌ای که ترکیب همه موارد قبلی است.

و البته آخرین روش معمولا بیشترین کاربرد را دارد. دلیل اصلی این که قهمیدن SVMها در نگاه اول کمی گیج کننده به نظر می‌رسد هم همین موضو ع است که ‌آن‌ها از چندین قطعه تسکیل شده اند که در طول زمان به ‌‌آن‌ها چیزهایی اضافه شده است.

به همین دلیل است که وقتی از یک زبان برنامه‌‌نویسی استفاده می‌کنید می‌پرسید از کدام کرنل باید استفاده کنیم(بخاطر کرنل‌های مختلفی که وجود دارند) و یا کدام مقدار ابرپارامتر C را باید استفاده کنید(برای کنترل تاثیر حاشیه نرم).

رگرسیون

در سال ۱۹۹۶، واپنیک و همکارانش، نسخه‌ای از SVM را پیشنهاد دادند که به جای طبقه‌بندی، عمل رگرسیون را انجام می‌دهد. این مورد به Support Vector Regression یا SVR معروف است. همانند SVM در این مدل نیز از کلک کرنل و ابرپارامتر C استفاده می‌شود.

در آینده مقاله ساده‌ای در مورد توضیح چگونگی استفاده از SVR در زبان R خواهم نوشت و آدرس آن را همین‌جا قرار خواهم داد.

اگر علاقمند هستید که راجع به SVR بیشتر بدانیند، می‌توانید به این آموزش خوب که نوشته Smola and Schölkopft است، مراجعه کنید.

خلاصه تاریخچه

طبقه‌بندی کننده حاشیه حداکثر (۱۹۶۳ یا ۱۹۷۹)
کلک کرنل (۱۹۹۲)
طبقه‌بندی کننده حاشیه نرم (۱۹۹۵)
رگرسیون بردار پشتیبان (۱۹۹۶)

در صورتی که مایلید بیشتر راجع به تاریخچه بدانید، می‌توانید به مقاله مرور همراه با جزییات از تاریخچه مراجعه کنید.

انواع دیگری از ماشین‌های بردار پشتیبان

به دلیل این که SVMها در طبقه‌بندی خیلی موفق بودند، مردم شروع به فکر کردن راجع به این موضوع کردند که چطور می‌توانند از همین منطق در انواع دیگر مسائل استفاده کنند یا این‌ که چطور مشتقات آن را ایجاد کنند. در نتیجه چندین روش مختلف و جالب در خانواده SVM به وجود آمد.

ماشین بردار پشتیبان ساخت‌یافتهکه توانایی پیش‌بینی اشیای ساخت‌یافته را دارد.
ماشین بردار پشتیبان حداقل مربعکه در طبقه‌بندی و رگرسیون استفاده می‌شود.
خوشه‌بندی بردار پشتیبانکه در تحلیل خوشه استفاده می‌شود.
ماشین بردار پشتیبان هدایتیکه در یادگیری نیمه نظارت‌شده استفاده می‌شود.
SVM رتبه‌بندیبرای مرتب کردن نتایج.
ماشین بردار پشتیبان تک کلاسهکه برای تشخیص ناهنجاری استفاده می‌شود.

نتیجه‌گیری

دیدیم که سختی در درک کردن این که SVMها دقیقا چه چیزی هستند، امری طبیعی است. علتش هم این است که چندین SVM برای چندین منظور وجود دارند. مثل همیشه تاریخ به ما اجازه می‌دهد که دید بهتری راجع به چگونگی به وجود آمدن SVMهایی که امروزه وجود دارند، داشته باشیم.

امیدوارم این مقاله دید وسیع‌تری از چشم‌انداز SVM به شما داده باشد و کمک کرده باشد که بهتر این ماشین‌ها را بشناسید و درک کنید.

اگه مایلید که بیشتر راجع به نحوه کار SVM در طبقه‌بندی بدانید، می‌توانید به آموزش‌های ریاضی مربوط به آن مراجعه کنید.

دسامبر 15, 2019/0 دیدگاه /توسط hgadmin

ماشین بردار پشتیبان (svm) قسمت 1

آموزش عمومی پردازش تصویر و بینایی ماشین

ماشین بردار پشتیبانی

ماشین بردار پشتیبان (Support vector machines – SVMs) یکی از روش‌های یادگیری بانظارت است که از آن برای طبقه‌بندی و رگرسیون استفاده می‌کنند.

این روش از جملهٔ روش‌های نسبتاً جدیدی است که در سال‌های اخیر کارایی خوبی نسبت به روش‌های قدیمی‌تر برای طبقه‌بندی از جمله شبکه‌های عصبی پرسپترون نشان داده است. مبنای کاریدسته‌بندی کنندۀ SVM دسته‌بندی خطی داده‌ها است و در تقسیم خطی داده‌ها سعی می‌کنیم خطی را انتخاب کنیم که حاشیه اطمینان بیشتری داشته باشد. حل معادله پیدا کردن خط بهینه برای داده‌ها به وسیله روش‌های QP که روش‌های شناخته شده‌ای در حل مسائل محدودیت‌دار هستند صورت می‌گیرد. قبل از تقسیمِ خطی برای اینکه ماشین بتواند داده‌های با پیچیدگی بالا را دسته‌بندی کند داده‌ها را به وسیلهٔ تابعِ phi به فضای با ابعاد خیلی بالاتر می‌بریم. برای اینکه بتوانیم مسئله ابعاد خیلی بالا را با استفاده از این روش‌ها حل کنیم از قضیه دوگانی لاگرانژ برای تبدیلِ مسئلهٔ مینیمم‌سازی مورد نظر به فرم دوگانی آن که در آن به جای تابع پیچیدهٔ phi که ما را به فضایی با ابعاد بالا می‌برد، تابعِ ساده‌تری به نامِ تابع هسته که ضرب برداری تابع phi است ظاهر می‌شود استفاده می‌کنیم. از توابع هسته مختلفی از جمله هسته‌های نمایی، چندجمله‌ای و سیگموید می‌توان استفاده نمود.

یکی از معروفترین خودآموزها مربوط به است.

کاربردهای SVM

الگوریتم SVM، جز الگوریتم‌های تشخیص الگو دسته بندی می‌شود.از الگوریتم SVM، در هر جایی که نیاز به تشخیص الگو یا دسته بندی اشیا در کلاس‌های خاص باشد می‌توان استفاده کرد.در ادامه به کاربردهای این الگوریتم به صورت موردی اشاره می‌شود:

سیستم آنالیز ریسک، کنترل هواپیما بدون خلبان، ردیابی انحراف هواپیما، شبیه‌سازی مسیر، سیستم راهنمایی اتوماتیک اتومبیل، سیستم‌های بازرسی کیفیت، آنالیز کیفیت جوشکاری، پیش‌بینی کیفیت، آنالیز کیفیت کامپیوتر، آنالیز عملیاتهای آسیاب، آنالیز طراحی محصول شیمیایی، آنالیز نگهداری ماشین، پیشنهاد پروژه، مدیریت و برنامه‌ریزی، کنترل سیستم فرایند شیمیایی و دینامیکی، طراحی اعضای مصنوعی، بهینه‌سازی زمان پیوند اعضا، کاهش هزینه بیمارستان، بهبود کیفیت بیمارستان، آزمایش اتاق اورژانس، اکتشاف روغن و گاز، کنترل مسیر در دستگاه‌های خودکار، ربات، جراثقال، سیستم‌های بصری، تشخیص صدا، اختصار سخن، کلاسه بندی صوتی، آنالیز بازار، سیستم‌های مشاوره‌ای محاسبه هزینه موجودی، اختصار اطلاعات و تصاویر، خدمات اطلاعاتی اتوماتیک، مترجم لحظه‌ای زبان، سیستم‌های پردازش وجه مشتری، سیستم‌های تشخیص ترمز کامیون، زمانبندی وسیله نقلیه، سیستم‌های مسیریابی، کلاسه بندی نمودارهای مشتری/بازار، تشخیص دارو، بازبینی امضا، تخمین ریسک وام، شناسایی طیفی، ارزیابی سرمایه، کلاسه بندی انواع سلول‌ها، میکروبها و نمونه ها، پیش‌بینی فروشهای آینده، پیش‌بینی نیازهای محصول، پیش‌بینی وضعیت بازار، پیش‌بینی شاخصهای اقتصادی، پیش‌بینی ملزومات انرژی، پیش‌بینی واکنش‌های دارویی، پیش‌بینی بازتاب محصولات شیمیایی، پیش‌بینی هوا، پیش‌بینی محصول، پیش‌بینی ریسک محیطی، پیش‌بینی جداول داوری، مدل کردن کنترل فرایند، آنالیز فعالیت گارانتی، بازرسی اسناد، تشخیص هدف، تشخیص چهره، انواع جدید سنسورها، دستگاه کاشف زیر دریایی بوسیله امواج صوتی، رادار، پردازش سیگنالهای تصویری شامل مقایسه اطلاعات، پیگیری هدف، هدایت جنگ افزارها، تعیین قیمت وضعیت فعلی، جلوگیری از پارازیت، شناسایی تصویر /سیگنال، چیدمان یک مدار کامل، بینایی ماشین، مدل کردن غیر خطی، ترکیب صدا، کنترل فرایند ساخت، آنالیز مالی، پیش‌بینی فرایندهای تولید، ارزیابی بکارگیری یک سیاست، بهینه‌سازی محصول، تشخیص ماشین و فرایند، مدل کردن کنترل سیستم‌ها، مدل کردن ساختارهای شیمیایی، مدل کردن سیستم‌های دینامیکی، مدل کردن سیگنال تراکم، مدل کردن قالب‌سازی پلاستیکی، مدیریت قراردادهای سهام، مدیریت وجوه بیمه، دیریت سهام، تصویب چک بانکی، اکتشاف تقلب در کارت اعتباری، ثبت نسیه، بازبینی امضا از چکها، پیش‌بینی ارزش نسیه، مدیریت ریسک رهن، تشخیص حروف و اعدا، تشخیص بیماری و…..

تاریخچه

الگوریتم SVM اولیه در ۱۹۶۳ توسط Vladimir Vapnik ابداع شدو در سال ۱۹۹۵ توسط Vapnik و Corinna Cortes برای حالت غیرخطی تعمیم داده شد.

خلاصه استفاده عملی از SVM

ماتریس الگو را آماده می کنیم. تابع کرنلی را برای استفاده انتخاب می کنیم. پارامتر تابع کرنل و مقدار C را انتخاب می کنیم. برای محاسبه ی مقادیرα_i الگوریتم آموزشی را با استفاده از حل‌کننده‌های QP اجرا می کنیم. داده‌های جدید با استفاده از مقادیرα_i و بردارهای پشتیبان می‌توانند دسته بندی شوند.

مزایا و معایب SVM

آموزش نسبتاً ساده است برخلاف شبکه‌های عصبی در ماکزیمم‌های محلی گیر نمی‌افتد. برای داده‌های با ابعاد بالا تقریباً خوب جواب می‌دهد. مصالحه بین پیچیدگی دسته بندی‌کننده و میزان خطا به‌طور واضح کنترل می‌شود. به یک تابع کرنل خوب و انتخاب پارامتر C نیاز دارد.

ماشین بردار پشتیبان خطی

شکل 1

ما مجموعه داده‌های آزمایش ${\mathcal {D}}$ شامل n عضو(نقطه)را در اختیار داریم که به صورت زیر تعریف می‌شود:

{\mathcal {D}}=\left\{(\mathbf {x} _{i},y_{i})\mid \mathbf {x} _{i}\in \mathbb {R} ^{p},\,y_{i}\in \{-1,1\}\right\}_{i=1}^{n}

جایی که مقدار $y$ برابر ۱ یا -۱ و هر $\mathbf {x} _{i}$ یک بردار حقیقی p-بعدی است. هدف پیدا کردن ابرصفحه جداکننده با بیشترین فاصله از نقاط حاشیه‌ای است که نقاط با $y_{i}=1$ را از نقاط با $y_{i}=-1$ جدا کند. هر ابر صفحه می‌تواند به صورت مجموعه‌ای از نقاط ${\mathbf {x}}$ که شرط زیر را ارضا می‌کند نوشت:

\mathbf {w} \cdot \mathbf {x} -b=0,\,

جایی که . علامت ضرب است.

{\mathbf {w} }

بردار نرمال است، که به ابرصفحه عمود است. ما می خواهیم

{\mathbf {w} }

{\mathbf {b} }

را طوری انتخاب کنیم که بیشترین فاصله بین ابر صفحه‌های موازی که داده‌ها را از هم جدا می‌کنند، ایجاد شود. این ابرصفحه‌ها با استفاده از رابطه زیر توصیف می‌شوند.

\mathbf {w} \cdot \mathbf {x} -b=1\,

\mathbf {w} \cdot \mathbf {x} -b=-1.\,

اگر داده‌های آموزشی جدایی پذیر خطی باشند، ما می‌توانیم دو ابر صفحه در حاشیه نقاط به‌طوری‌که هیچ نقطه مشترکی نداشته باشند، در نظر بگیریم و سپس سعی کنیم، فاصله آن‌ها را، ماکسیمم کنیم. با استفاده از هندسه، فاصله این دو صفحه

{\tfrac {2}{\|\mathbf {w} \|}}

است. بنابراین ما باید

\|\mathbf {w} \|

را مینیمم کنیم. برای اینکه از ورود نقاط به حاشیه جلوگیری کنیم، شرایط زیر را اضافه می کنیم: برای هر

i

of the first class

\mathbf {w} \cdot \mathbf {x} _{i}-b\geq 1\qquad {\text{ for }}\mathbf {x} _{i}

یا

of the second class

\mathbf {w} \cdot \mathbf {x} _{i}-b\leq -1\qquad {\text{ for }}\mathbf {x} _{i}

این می‌تواند به صورت زیر نوشته شود:

y_{i}(\mathbf {w} \cdot \mathbf {x} _{i}-b)\geq 1,\quad {\text{ for all }}1\leq i\leq n.\qquad \qquad (1)

با کنار هم قرار دادن این دو یک مسئله بهینه‌سازی به دست می‌آید:

Minimize (in ${\mathbf {w} ,b}$ )

\|\mathbf {w} \|

subject to (for any $i=1,\dots ,n$ )

y_{i}(\mathbf {w} \cdot \mathbf {x_{i}} -b)\geq 1.\,

فرم اولیه

مسئله بهینه‌سازی مشاهده شده در قسمت قبل، مسئله سختی، برای حل کردن است، زیرا به||w|| وابسته است (نرم w ) . خوشبختانه می‌توانیم، بدون تغییر در مسئله||w|| را با ${\tfrac {1}{2}}\|\mathbf {w} \|^{2}$ جانشین کنیم( عبارت ½ برای آسودگی در محاسبات ریاضی آورده شده). این یک مسئله بهینه سازی (OP)برنامه‌ریزی غیرخطی(QP) است. به‌طور واضح تر :

Minimize (in ${\mathbf {w} ,b}$ ) c

{\frac {1}{2}}\|\mathbf {w} \|^{2}

subject to (for any $i=1,\dots ,n$ )

y_{i}(\mathbf {w} \cdot \mathbf {x_{i}} -b)\geq 1.

می توان عبارت قبل را با استفاده از ضرایب نا منفی لاگرانژ به صورت زیر نوشت که در آن ضرایب لاگرانژ هستند $\alpha _{i}$ :

\min _{\mathbf {w} ,b,{\boldsymbol {\alpha }}}\{{\frac {1}{2}}\|\mathbf {w} \|^{2}-\sum _{i=1}^{n}{\alpha _{i}[y_{i}(\mathbf {w} \cdot \mathbf {x_{i}} -b)-1]}\}

اما فرمول فوق اشتباه است . فرض کنید ما بتوانیم خانواده‌ای از ابرصفحات که نقاط را تقسیم می‌کنند پیدا کنیم . پس همه $y_{i}(\mathbf {w} \cdot \mathbf {x_{i}} -b)-1\geq 0$ . بنا بر این ما می‌توانیم مینیمم را با فرستادن همه $\alpha _{i}$ به $+\infty$ پیدا کنیم. با این حال شرط پیش گفته می‌تواند به صورت پایین بیان شود:

\min _{\mathbf {w} ,b}\max _{\boldsymbol {\alpha }}\{{\frac {1}{2}}\|\mathbf {w} \|^{2}-\sum _{i=1}^{n}{\alpha _{i}[y_{i}(\mathbf {w} \cdot \mathbf {x_{i}} -b)-1]}\}

ما به دنبال نقاط saddle میگردیم.حالا می‌توان این مسئله را به کمک برنامه‌ریزی غیرخطی استاندارد حل کرد. جواب می‌تواند به صورت ترکیب خطی از بردارهای آموزشی بیان شود :

\mathbf {w} =\sum _{i=1}^{n}{\alpha _{i}y_{i}\mathbf {x_{i}} }

تنها چند $\alpha _{i}$ بزرگتر از صفر خواهد بود. $\mathbf {x_{i}}$ متناظر، دقیقاً همان بردار پشتیبان خواهد بود و به شرط را ارضا خواهد کرد. از این می‌توان نتیجه گرفت که بردارهای پشتیبان شرط زیر را نیز ارضا می‌کنند: $y_{i}(\mathbf {w} \cdot \mathbf {x_{i}} -b)=1$ که اجازه می دهد مفدار b تعریف شود. در عمل الگوریتم مقاوم تر خواهد بود اگر از تمام $N_{SV}$ بردار پشتیبان میانگین گرفته شود:

b={\frac {1}{N_{SV}}}\sum _{i=1}^{N_{SV}}{(\mathbf {w} \cdot \mathbf {x_{i}} -y_{i})}

فرم دوگان

استفاده از این واقعیت که $\|\mathbf {w} \|^{2}=w\cdot w$ و جانشینی $\mathbf {w} =\sum _{i=1}^{n}{\alpha _{i}y_{i}\mathbf {x_{i}} }$ می‌توان نشان داد که دوگان SVM به مسئله بهینه‌سازی زیر ساده می‌شود:

Maximize (in $\alpha _{i}$ )

{\tilde {L}}(\mathbf {\alpha } )=\sum _{i=1}^{n}\alpha _{i}-{\frac {1}{2}}\sum _{i,j}\alpha _{i}\alpha _{j}y_{i}y_{j}\mathbf {x} _{i}^{T}\mathbf {x} _{j}=\sum _{i=1}^{n}\alpha _{i}-{\frac {1}{2}}\sum _{i,j}\alpha _{i}\alpha _{j}y_{i}y_{j}k(\mathbf {x} _{i},\mathbf {x} _{j})

subject to (for any $i=1,\dots ,n$ )

\alpha _{i}\geq 0,\,

and to the constraint from the minimization in $b$

\sum _{i=1}^{n}\alpha _{i}y_{i}=0.

در اینجا هسته به صورت $k(\mathbf {x} _{i},\mathbf {x} _{j})=\mathbf {x} _{i}\cdot \mathbf {x} _{j}$ تعریف می‌شود. عبارت $\alpha$ تشکیل یک دوگان برای بردار وزن‌ها مجموعه آموزشی می دهد:

\mathbf {w} =\sum _{i}\alpha _{i}y_{i}\mathbf {x} _{i}.

ماشین بردار پشتیبان چند کلاسی

SVM اساساً یک جداکننده دودویی است. در بخش قبلی پایه‌های تئوری ماشین‌های بردار پشتیبان برای دسته بندی دو کلاس تشریح شد. یک تشخیص الگوی چند کلاسی می‌تواند به وسیله ی ترکیب ماشین‌های بردار پشیبان دو کلاسی حاصل شود. به‌طور معمول دو دید برای این هدف وجود دارد. یکی از آن‌ها استراتژی “یک در مقابل همه ” برای دسته بندی هر جفت کلاس و کلاس‌های باقی‌مانده‌است. دیگر استراتژی “یک در مقابل یک” برای دسته بندی هر جفت است. در شرایطی که دسته بندی اول به دسته بندی مبهم منجر می‌شود.برای مسائل چند کلاسی٬رهیافت کلی کاهش مسئله ی چند کلاسی به چندین مسئله دودویی است. هریک از مسائل با یک جداکننده دودویی حل می‌شود. سپس خروجی جداکننده‌های دودویی SVM با هم ترکیب شده و به این ترتیب مسئله چند کلاس حل می‌شود.

ماشین‌های بردار پشتیبان غیرخطی

ابرصفحه جداکننده بهینه اولین بار توسط Vapnik در سال ۱۹۶۳ ارائه شد که یک دسته‌کننده خطی بود. در سال ۱۹۹۲ ،Bernhard Boser ، Isabelle GuyonوVapnik راهی را برای ایجاد دسته بند غیرخطی، با استفاده قرار دادن هسته برای پیدا کردن ابرصفحه با بیشتر حاشیه، پیشنهاد دادند. الگوریتم نتیجه شده ظاهراً مشابه است، به جز آنکه تمام ضرب‌های نقطه‌ای با یک تابع هسته غیرخطی جایگزین شداند. این اجازه می‌دهد، الگوریتم، برای ابرصفحه با بیشترین حاشیه در یک فضای ویژگی تغییرشکل داده، مناسب باشد. ممکن است، تغییرشکل غیرخطی باشد و فضای تغییر یافته، دارای ابعاد بالاتری باشد. به هر حال دسته‌کننده، یک ابرصفحه در فضای ویژگی با ابعاد بالا است، که ممکن است در فضای ورودی نیز غیرخطی باشد.

اگر از هسته با تابع گوسیین استفاده شود، فضای ویژگی متناظر، یک فضای هیلبرت نامتناهی است. دسته‌کننده ی بیشترین حاشیه، خوش ترتیب است، بنابراین ابعاد نامتناهی، نتیجه را خراب نمی‌کند. هسته‌های متداول به صورت زیر هستند:

چندجمله‌ای (همگن): $k(\mathbf {x_{i}} ,\mathbf {x_{j}} )=(\mathbf {x_{i}} \cdot \mathbf {x_{j}} )^{d}$
چندجمله‌ای (ناهمگن): $k(\mathbf {x_{i}} ,\mathbf {x_{j}} )=(\mathbf {x_{i}} \cdot \mathbf {x_{j}} +1)^{d}$
گوسیین Radial Basis Function: $k(\mathbf {x_{i}} ,\mathbf {x_{j}} )=\exp(-\gamma \|\mathbf {x_{i}} -\mathbf {x_{j}} \|^{2})$ ، for $\gamma >0.$ Sometimes parametrized using $\gamma =1/{2\sigma ^{2}}$
تانژانت هذلولی: $k(\mathbf {x_{i}} ,\mathbf {x_{j}} )=\tanh(\kappa \mathbf {x_{i}} \cdot \mathbf {x_{j}} +c)$ ، for some (not every) $\kappa >0$ and $c<0$

هسته با انتقال $\varphi (\mathbf {x_{i}} )$ با تساوی $k(\mathbf {x_{i}} ,\mathbf {x_{j}} )=\varphi (\mathbf {x_{i}} )\cdot \varphi (\mathbf {x_{j}} )$ در ارتباط است. همچنین مقدار wدر فضای انتقال یافته برابر $\textstyle \mathbf {w} =\sum _{i}\alpha _{i}y_{i}\varphi (\mathbf {x} _{i}).$ است. ضرب نقطه‌ای با w می‌تواند توسط هسته محاسبه شود یعنی $\textstyle \mathbf {w} \cdot \varphi (\mathbf {x} )=\sum _{i}\alpha _{i}y_{i}k(\mathbf {x} _{i},\mathbf {x} )$ . به هر حال در حالت عادی w’ وجود ندارد، به‌طوری‌که $\mathbf {w} \cdot \varphi (\mathbf {x} )=k(\mathbf {w'} ,\mathbf {x} ).$

منبع

ماشین بردار پشتیبان (svm) قسمت 1
ماشین بردار پشتیبان (svm) قسمت 2
ماشین بردار پشتیبان (svm) قسمت 3

دسامبر 14, 2019/0 دیدگاه /توسط daliri

خوشه بندی (Clustering) قسمت 4

آموزش عمومی پردازش تصویر و بینایی ماشین

خوشه‌بندی سلسله مراتبی (Hierarchical Clustering)

برعکس خوشه‌بندی تفکیکی که اشیاء را در گروه‌های مجزا تقسیم می‌کند، «خوشه‌بندی سلسله مراتبی» (Hierarchical Clustering)، در هر سطح از فاصله، نتیجه خوشه‌بندی را نشان می‌دهد. این سطوح به صورت سلسله مراتبی (Hierarchy) هستند.

برای نمایش نتایج خوشه‌بندی به صورت سلسله مراتبی از «درختواره» (Dendrogram) استفاده می‌شود. این شیوه، روشی موثر برای نمایش نتایج خوشه‌بندی سلسله مراتبی است. در تصویر ۲ نتایج خوشه‌بندی سلسله مراتبی روی داده‌های $s = 1, 3, 6, 2, 8, 10$ با استفاده از درختواره را می‌بینید.

تصویر ۲- نمودار دختواره برای داده‌های مربوط s=1,3,6,2,8,10

همانطور که در تصویر ۲ قابل رویت است،‌ ابتدا هر مقدار یک خوشه محسوب می‌شود. در طی مراحل خوشه‌بندی، نزدیکترین مقدارها (براساس تابع فاصله تعریف شده) با یکدیگر ادغام شده و خوشه جدیدی می‌سازند.

در نتیجه براساس تصویر ۲ ابتدا در مرحله اول مقدار اول و چهارم تشکیل اولین خوشه را می‌دهند، زیرا کمترین فاصله را دارند. سپس در مرحله دو، مقدار دوم با خوشه تشکیل شده در مرحله اول ترکیب می‌شود. در مرحله سوم مقدارهای سوم و ششم با هم تشکیل یک خوشه می‌دهند که در مرحله چهارم با مقدار پنجم ترکیب شده و خوشه جدیدی می‌سازند.

در انتها نیز خوشه تشکیل شده در مرحله دوم با خوشه تشکیل شده در مرحله چهارم ادغام شده و خوشه نهایی را ایجاد می‌کنند. همانطور که دیده می‌شود با داشتن شش مقدار خوشه‌بندی سلسله مراتبی، پنچ مرحله خواهد داشت زیرا در هر مرحله فقط یک عمل ادغام انجام می‌شود.

نکته: توجه داشته باشید که مقدارهایی که روی محور افقی دیده می‌شوند، بیانگر موقعیت مقدارها در لیست داده‌ها است و نه خود مقادیر. همچنین محور عمودی نیز فاصله یا ارتفاع بین خوشه‌ها را نشان می‌دهد.

در الگوریتم خوشه‌بندی سلسله مراتبی معمولا با کوچکترین خوشه‌ها شروع می‌کنیم. به این معنی که در ابتدا هر مقدار بیانگر یک خوشه است. سپس دو مقداری که بیشترین شباهت (کمترین فاصله) را دارند با یکدیگر ادغام شده و یک خوشه جدید می‌سازند. بعد از این مرحله، ممکن است دو مقدار یا یک مقدار با یک خوشه یا حتی دو خوشه با یکدیگر ادغام شده و خوشه جدیدی ایجاد کنند.

این عملیات با رسیدن به بزرگترین خوشه که از همه مقدارها تشکیل یافته پایان می‌یابد. به این ترتیب اگر n مقدار داشته باشیم در مرحله اول تعداد خوشه‌ها برابر با n‌ است و در آخرین مرحله یک خوشه باقی خواهد ماند.

برای اندازه‌گیری فاصله بین دو خوشه یا یک مقدار با یک خوشه از روش‌های «پیوند» (Linkage) استفاده می‌شود. از انواع روش‌های پیوند می‌توان به «نزدیکترین همسایه» (Nearest Neighbor) یا «پیوند تکی» (Single Linkage)، «دورترین همسایه» (Furthest Neighbor) یا «پیوند کامل» (Complete Linkage) و همچنین «پیوند میانگین» (Average Linkage) اشاره کرد.

معمولا به این شیوه خوشه‌بندی سلسله مراتبی، روش «تجمیعی» (Agglomerative) می‌گویند.

برعکس اگر عمل خوشه‌بندی سلسله مراتبی به شکلی باشد که با بزرگترین خوشه، عملیات خوشه‌بندی شروع شده و با تقسیم هر خوشه به خوشه‌های کوچکتر ادامه پیدا کند، به آن «خوشه‌بندی سلسله مراتبی تقسیمی» (Divisive Hierarchical Clustering) می‌گویند. در آخرین مرحله این روش، هر مقدار تشکیل یک خوشه را می‌دهد پس n خوشه خواهیم داشت.

هر چند شیوه نمایش خوشه‌بندی سلسله مراتبی تقسیمی نیز توسط درختواره انجام می‌شود ولی از آنجایی که محدودیت‌هایی برای تقسیم یک خوشه به زیر خوشه‌های دیگر وجود دارد، روش تقسیمی کمتر به کار می‌رود.

نکته: در شیوه خوشه‌بندی سلسله مراتبی، عمل برچسب گذاری در طی مراحل خوشه‌بندی اصلاح پذیر نیست. به این معنی که وقتی عضوی درون یک خوشه قرار گرفت هرگز از آن خوشه خارج نمی‌شود.

از الگوریتم‌های معروف برای خوشه‌بندی سلسله مراتبی تجمیعی می‌توان به AGNES و برای تقسیمی به DIANA اشاره کرد.

خوشه‌بندی برمبنای چگالی (Density-Bases Clustering)

روش‌های خوشه‌بندی تفکیکی قادر به تشخیص خوشه‌هایی کروی شکل هستند. به این معنی که برای تشخیص خوشه‌ها از مجموعه داده‌هایی به شکل‌های «کوژ» (Convex) یا محدب خوب عمل می‌کنند. در عوض برای تشخیص خوشه‌ها برای مجموعه داده‌های «کاو» (Concave) یا مقعر دچار خطا می‌شوند. به تصویر ۳ توجه کنید که بیانگر شکل‌های کاو است.

تصویر ۳- مقایسه نتایج خوشه‌بندی تفکیکی با روش چگالی

همانطور که دیده می‌شود میانگین هر دو خوشه در روش k-means در محلی قرار گرفته است که مربوط به خوشه‌ دیگر است. در حالی که خوشه‌بندی برمبنای چگالی به خوبی نقاط را در خوشه‌های درست قرار داده است.

در الگوریتم‌ها خوشه‌بندی برمبنای چگالی، نقاط با تراکم زیاد شناسایی شده و در یک خوشه قرار می‌گیرند. از الگوریتم‌های معروف در این زمینه می‌توان به DBSCAN اشاره کرد که در سال ۱۹۹۶ توسط «استر» (Ester) معرفی شد.

این الگوریتم توانایی شناسایی نقاط دورافتاده را داشته و می‌تواند تاثیر آن‌ها را در نتایج خوشه‌بندی از بین ببرد. شیوه کارکرد این الگوریتم‌ بنا به تعریف‌های زیر قابل درک است:

همسایگی به شعاع : اگر فضای با شعاع $ϵ$ را حول نقطه‌ای x در نظر بگیریم، یک همسایگی ایجاد کرده‌ایم که به شکل $N_{ϵ} (x)$ نشان داده می‌شود. شکل ریاضی این همسایگی به صورت زیر است.

$N_{ϵ} (x) = {y \in D; d (x, y) \leq ϵ}$

بطوری که D مجموعه داده و d تابع فاصله است. تصویر 4 مفهوم همسایگی را نشان می‌دهد.

تصویر ۴- همسایگی و شعاع همسایگی

قابل دسترسی مستقیم (Directly density-reachable): نقطه x را قابل دسترسی مستقیم از y می‌نامند اگر براساس دو پارامتر $N_{m i n}$ و $ϵ$ داشته باشیم:

$x \in N_{ϵ} (y)$

$| N_{ϵ} (y) | \geq N_{m i n}$

در اینجا $| N_{ϵ} (y)$ نشانگر تعداد اعضای همسایگی به شعاع $ϵ$ از نقطه y است.

پس شرط اول به معنی این است که x در همسایگی از y قرار دارد و شرط دوم نیز بیان می‌کند که باید تعداد اعضای همسایگی y از حداقل تعداد اعضای همسایگی بیشتر باشد.

نقطه قابل دسترسی (Density-Reachable): نقطه x را از طرق y‌ نامیده می‌شود، اگر دنباله‌ای از نقاط مثل $x_{1}, x_{2}, \dots, x_{i}$ موجود باشند که نقطه x را به y برسانند. یعنی:

$x = x_{1}, x_{2}, \dots, x_{i} = y$

در این حالت برای مثال $x_{1}$ «قابل دسترسی مستقیم» (Direct Reachable) به $x_{2}$ ‌ نامیده می‌شود.

نقاط متصل (Density-Connected): دو نقطه x و y را متصل گویند اگر براساس پارامترهای $ϵ$ و $N_{m i n}$ نقطه‌ای مانند z وجود داشته باشد که هر دو نقطه x و y از طریق آن قابل دسترسی باشند.
خوشه (Cluster): فرض کنید مجموعه داده D موجود باشد. همچنین C یک زیر مجموعه غیر تهی از D‌ باشد. C را یک خوشه می‌نامند اگر براساس پارمترهای $ϵ$ و $N_{m i n}$ در شرایط زیر صدق کند:

۱- اگر x درون C باشد و y نیز قابل دسترسی به x با پارامترهای $ϵ$ و $N_{m i n}$ باشد، آنگاه y نیز در C‌ است.

۲- اگر دو نقطه x و y در C باشند آنگاه این نقاط براساس پارامترهای $ϵ$ و $N_{m i n}$ نقاط متصل محسوب شوند.

به این ترتیب خوشه‌ها شکل گرفته و براساس میزان تراکمشان تشکیل می‌شوند. نویز یا نوفه (Noise) نیز نقاطی خواهند بود که در هیچ خوشه‌ای جای نگیرند. برای روشن شدن این تعریف‌ها به تصویر 5 توجه کنید.

تصویر ۵- نقاط مرکزی، مرزی، نوفه (نویز)

نکته: با توجه به تعریف خوشه، مشخص است که اندازه هر خوشه از $N_{m i n}$ بیشتر است.

مراحل خوشه‌بندی برمبنای چگالی به این ترتیب است که ابتدا یک نقطه را به صورت اختیاری انتخاب کرده و نقاط قابل دسترس برای آن پیدا می‌شود. اگر x یک نقطه مرکزی باشد (نقطه‌ای که درون خوشه قرار داشته باشد)، خوشه را تشکیل می‌دهد ولی اگر x نقطه‌ای مرزی باشد (نقطه‌ای که در لبه‌های خوشه قرار داشته باشد) آنگاه هیچ نقطه‌ قابل دسترسی برای x وجود نخواهد داشت و الگوریتم از نقطه‌ای دیگری ادامه پیدا می‌کند.

در مراحل خوشه‌بندی ممکن است دو خوشه که به یکدیگر نزدیک باشند، ادغام شوند. فاصله بین دو خوشه برحسب حداقل فاصله بین اعضای دو خوشه (پیوند تکی) سنجیده می‌شود.

نکته: انتخاب مقدار برای پارامترهای $ϵ$ و $N_{m i n}$ مسئله مهمی است که براساس نظر محقق باید به الگوریتم داده شوند. ترسیم نمودار داده‌ها در انتخاب این پارامترها می‌تواند موثر باشد. هرچه داده‌ها در دسته‌های متراکم‌تر دیده شوند بهتر است مقدار $ϵ$ را کوچک در نظر گرفت و اگر لازم است که تعداد خوشه‌ها کم باشند بهتر است مقدار $N_{m i n}$ را بزرگ انتخاب کرد.

خوشه‌بندی برمبنای مدل (Model-Based Clustering)

در روش‌های پیشین، فرضیاتی مبنی بر وجود یک توزیع آماری برای داده‌ها وجود نداشت. در روش «خوشه‌بندی برمبنای مدل» (Model-Based Clustering) یک توزیع آماری برای داده‌ها فرض می‌شود. هدف در اجرای خوشه‌بندی برمبنای مدل، برآورد پارامترهای توزیع آماری به همراه متغیر پنهانی است که به عنوان برچسب خوشه‌ها در مدل معرفی شده.

با توجه به تعداد خوشه‌هایی که در نظر گرفته شده است، مثلا k، تابع درستنمایی را برای پیدا کردن خوشه‌ها به صورت زیر می‌نویسند:

$L_{M} (Θ_{1}, Θ_{2}, Θ_{3}, \dots, Θ_{k}; t_{1}, t_{2}, \dots, t_{k}) = n \prod i = 1 k \sum j = 1 t_{j} f_{j} (x_{i}, Θ_{j})$

در رابطه بالا $t_{j}$ بیانگر احتمال تعلق نقطه به خوشه jام و $f_{j}$ نیز توزیع آمیخته با پارامترهای $Θ_{j}$ است.

در اکثر مواقع برای داده‌ها توزیع نرمال آمیخته در نظر گرفته می‌شود. در چنین حالتی توزیع آمیخته را به فرمی می‌نویسند که درصد آمیختگی (درصدی از داده‌ها که متعلق به هر توزیع هستند) نیز به عنوان پارامتر در مدل حضور دارد.

$f (x) = k \sum j = 1 p_{j} Φ (X; μ_{j}, Σ_{i})$

در رابطه بالا $Φ$ توزیع نرمال با پارامترهای $μ_{j}$ و $Σ_{j}$ برای توزیع jام هستند و $p_{j}$ ‌ نیز درصد آمیختگی برای توزیع jام محسوب می‌شود. در تصویر 6 یک نمونه از توزیع آمیخته نرمال دو متغیره نمایش داده شده است.

تصویر ۶- توزیع آمیخته نرمال دو متغیره

انتخاب‌های مختلفی برای ماتریس واریانس-کوواریانس یا $Σ$ وجود دارد. یکی از این حالت‌ها در نظر گرفتن استقلال و یکسان بودن واریانس برای همه توزیع‌ها است. همچنین می‌توان واریانس هر توزیع را متفاوت از توزیع‌های دیگر در نظر گرفت و بدون شرط استقلال عمل کرد. در حالت اول پیچیدگی مدل و تعداد پارامترهای برآورد شده کم و در حالت دوم پیچیدگی مدل و تعداد پارامترهای برآورده شده زیاد خواهد بود.

برای برآورد پارامترهای چنین مدلی باید از تابع درستنمایی استفاده کرد و به کمک مشتق مقدار حداکثر را برای این تابع بدست آورد. با این کار پارامترهای مدل نیز برآورد می‌شوند. ولی با توجه به پیچیدگی تابع درستنمایی می‌توان از روش‌هایی ساده‌ و سریع‌تری نیز کمک گرفت. یکی از این روش‌ها استفاده از الگوریتم EM‌ (مخفف Expectation Maximization) است. در الگوریتم EM که براساس متغیر پنهان عمل می‌کند، می‌توان به حداکثر مقدار تابع درستنمایی همراه با برآورد پارامترها دست یافت.

در چنین حالتی می‌توان برچسب تعلق هر مقدار به خوشه را به عنوان متغیر پنهان در نظر گرفت. اگر متغیر پنهان را $z_{i j}$ ‌ در نظر بگیریم مقداری برابر با ۱ دارد اگر مشاهده iام در خوشه jام باشد و در غیر اینصورت مقدار آن 0 خواهد بود.

منبع

منابع

1.https://fa.wikipedia.org

2.https://tik4.com

3.https://blog.faradars.org

خوشه بندی (Clustering) قسمت 1
خوشه بندی (Clustering) قسمت 2
خوشه بندی (Clustering) قسمت 3
خوشه بندی (Clustering) قسمت 4

دسامبر 10, 2019/0 دیدگاه /توسط hgadmin

خوشه بندی (Clustering) قسمت 3

آموزش عمومی پردازش تصویر و بینایی ماشین

هدف از خوشه بندی چیست؟

همانطور که می‌دانید از داده‌ کاوی برای کاوش در اطلاعات و کشف دانش استفاده می‌شود. برای اینکار الگوریتم‌های متعددی وجود دارد که هر یک برای هدف خاصی کاربرد دارند

خوشه بندی چیست؟

خوشه بندی

کلاسترینگ(Clustering) یا خوشه‌ بندی از جمله الگوریتم‌های قطعه بندی به حساب می‌آید. الگوریتم خوشه‌بندی اطلاعاتی را که ویژگی‌های نزدیک به هم و مشابه دارند را در دسته‌های جداگانه که به آن خوشه گفته می‌شود قرار می‌دهد. به بیان دیگر خوشه‌بندی همان دسته‌بندی‌های ساده‌ای است که در کارهای روزانه انجام می‌دهیم. وقتی با یک مجموعه کوچک از صفات روبرو باشیم دسته بندی به سادگی قابل اجرا است، برای مثال در یک مجموعه ‌از خودکارهای آبی، مشکی، قرمز و سبز به راحتی می‌توانیم آن‌ها را در ۴ دسته قرار دهیم اما اگر در همین مجموعه ویژگی‌های دیگری مثل سایز، شرکت سازنده، وزن، قیمت و… مطرح باشد کار کمی پیچیده می‌شود. حال فرض کنید در یک مجموعه متشکل از هزاران رکورد و صدها ویژگی قصد دسته بندی دارید، چگونه باید این کار را انجام دهید؟!

بخش بندی داده‌ها به گروه‌ها یا خوشه‌های معنادار به طوری که محتویات هر خوشه ویژگی‌های مشابه و در عین حال نسبت به اشیاء دیگر در سایر خوشه‌ها غیر مشابه باشند را خوشه‌بندی می‌گویند. از این الگوریتم در مجموعه داده‌های بزرگ و در مواردی که تعداد ویژگی‌های داده زیاد باشد استفاده می‌شود.

هدف خوشه بندی (Clustering) یافتن خوشه های مشابه از اشیاء در بین نمونه های ورودی می باشد اما چگونه می توان گفت که یک خوشه بندی مناسب است و دیگری مناسب نیست؟ در حقیقت سوال اصلی این است که کدام روش خوشه بندی برای هر مجموعه داده ای مناسب خواهد بود؟ می توان نشان داد که هیچ معیار مطلقی برای بهترین خوشه بندی وجود ندارد بلکه این بستگی به مساله و نظر کاربر دارد که باید تصمیم بگیرد که آیا نمونه ها بدرستی خوشه بندی شده اند یا خیر؟ با این حال معیار های مختلفی برای خوب بودن یک خوشه بندی ارائه شده است که می تواند کاربر را برای رسیدن به یک خوشه بندی مناسب راهنمایی کند که در بخشهای بعدی چند نمونه از این معیارها آورده شده است. یکی از مسایل مهم در خوشه بندی انتخاب تعداد خوشه ها می باشد. در بعضی از الگوریتم ها تعداد خوشه ها از قبل مشخص شده است و در بعضی دیگر خود الگوریتم تصمیم می گیرد که داده ها به چند خوشه تقسیم شوند.

خوشه بندی داده ها

خوشه بندی یا Clustering یکی از شاخه های یادگیری بدون نظارت (Unsupervised) می باشد و فرآیند خود کاری است که در طی آن، نمونه ها به دسته هایی که اعضای آن مشابه یکدیگر می باشند تقسیم می شوند که به این دسته ها خوشه (Cluster) گفته می شود. بنابراین خوشه مجموعه ای از اشیاء می باشد که در آن اشیاء با یکدیگر مشابه بوده و با اشیاء موجود در خوشه های دیگر غیر مشابه می باشند. برای مشابه بودن می توان معیارهای مختلفی را در نظر گرفت مثلا می توان معیار فاصله را برای خوشه بندی مورد استفاده قرار داد و اشیائی را که به یکدیگر نزدیکتر هستند را بعنوان یک خوشه در نظر گرفت که به این نوع خوشه بندی، خوشه بندی مبتنی بر فاصله نیز گفته می شود. بعنوان مثال در شکل ۱ نمونه های ورودی در سمت چپ به چهار خوشه مشابه شکل سمت راست تقسیم می شوند. در این مثال هر یک از نمونه های ورودی به یکی از خوشه ها تعلق دارد و نمونه ای وجود ندارد که متعلق به بیش از یک خوشه باشد.

خوشه بندی

بعنوان یک مثال دیگر شکل ۲ را در نظر بگیرید در این شکل هر یک از دایره های کوچک یک وسیله نقلیه (شیء) را نشان می دهد که با ویژگی های وزن و حداکثر سرعت مشخص شده اند. هر یک از بیضی ها یک خوشه می باشد و عبارت کنار هر بیضی برچسب آن خوشه را نشان می دهد. کل دستگاه مختصات که نمونه ها در آن نشان داده شده اند را فضای ویژگی می گویند.

خوشه بندی

همانطور که در شکل می بینید وسایل نقلیه به سه خوشه تقسیم شده اند. برای هر یک از این خوشه ها می توان یک نماینده در نظر گرفت مثلا می توان میانگین وسایل نقلیه باری را محاسبه کرد و بعنوان نماینده خوشه وسایل نقلیه باری معرفی نمود. در واقع الگوریتمهای خوشه بندی اغلب بدین گونه اند که یک سری نماینده اولیه برای نمونه های ورودی در نظر گرفته می شود و سپس از روی میزان تشابه نمونه ها با این نماینده های مشخص می شود که نمونه به کدام خوشه تعلق دارد و بعد از این مرحله نماینده های جدید برای هر خوشه محاسبه می شود و دوباره نمونه ها با این نماینده ها مقایسه می شوند تا مشخص شود که به کدام خوشه تعلق دارند و این کار آنقدر تکرار می شود تا زمانیکه نماینده های خوشه ها تغییری نکنند.

خوشه بندی با طبقه بندی (Classification) متفاوت است. در طبقه بندی نمونه های ورودی برچسب گذاری شده اند ولی در خوشه بندی نمونه های ورودی دارای بر چسب اولیه نمی باشند و در واقع با استفاده از روشهای خوشه بندی است که داده های مشابه مشخص و بطور ضمنی برچسب گذاری می شوند. در واقع می توان قبل از عملیات طبقه بندی داده ها یک خوشه بندی روی نمونه ها انجام داد و سپس مراکز خوشه های حاصل را محاسبه کرد و یک بر چسب به مراکز خوشه ها نسبت داد و سپس عملیات طبقه بندی را برای نمونه های ورودی جدید انجام داد.

منبع

آشنایی با خوشه‌بندی (Clustering) و شیوه‌های مختلف آن

الگوریتم‌های متنوع و زیادی برای انجام عملیات خوشه‌بندی در داده‌کاوی به کار می‌رود. آگاهی از الگوریتم‌های خوشه‌بندی و آشنایی با نحوه اجرای آن‌ها کمک می‌کند تا مناسب‌ترین روش را برای خوشه‌بندی داده‌های خود به کار ببرید.

«تحلیل خوشه‌بندی» (Cluster Analysis) نیز مانند «تحلیل طبقه‌بندی» (Classification Analysis) در «یادگیری ماشین» (Machine Learning) به کار می‌رود. هر چند که تحلیل طبقه‌بندی یک روش «با ناظر» (Supervised) محسوب شده ولی خوشه‌بندی روشی «بدون ناظر» (Unsupervised) است.

در این متن، ابتدا خوشه‌بندی را تعریف می‌کنیم و سپس به معرفی گونه‌های مختلف الگوریتم‌های خوشه‌بندی می‌پردازیم.

خوشه‌بندی (Clustering)

«تحلیل خوشه‌بندی» (Cluster Analysis) یا بطور خلاصه خوشه‌بندی، فرآیندی است که به کمک آن می‌توان مجموعه‌ای از اشیاء را به گروه‌های مجزا افراز کرد. هر افراز یک خوشه نامیده می‌شود. اعضاء هر خوشه با توجه به ویژگی‌هایی که دارند به یکدیگر بسیار شبیه هستند و در عوض میزان شباهت بین خوشه‌ها کمترین مقدار است. در چنین حالتی هدف از خوشه‌بندی، نسبت دادن برچسب‌هایی به اشیاء است که نشان دهنده عضویت هر شیء به خوشه است.

به این ترتیب تفاوت اصلی که بین تحلیل خوشه‌بندی و «تحلیل طبقه‌بندی» (Classification Analysis) وجود دارد، نداشتن برچسب‌های اولیه برای مشاهدات است. در نتیجه براساس ویژگی‌های مشترک و روش‌های اندازه‌گیری فاصله یا شباهت بین اشیاء، باید برچسب‌هایی بطور خودکار نسبت داده شوند. در حالیکه در طبقه‌بندی برچسب‌های اولیه موجود است و باید با استفاده از الگوی‌های پیش‌بینی قادر به برچسب گذاری برای مشاهدات جدید باشیم.

با توجه به روش‌های مختلف اندازه‌گیری شباهت یا الگوریتم‌های تشکیل خوشه‌،‌ ممکن است نتایج خوشه‌بندی برای مجموعه داده ثابت متفاوت باشند. شایان ذکر است که تکنیک‌های خوشه‌بندی در علوم مختلف مانند، گیاه‌شناسی، هوش مصنوعی، تشخیص الگوهای مالی و … کاربرد دارند.

روش‌های خوشه‌بندی

اگر چه بیشتر الگوریتم‌ها یا روش‌های خوشه‌بندی مبنای یکسانی دارند ولی تفاوت‌هایی در شیوه اندازه‌گیری شباهت یا فاصله و همچنین انتخاب برچسب برای اشیاء هر خوشه در این روش‌ها وجود دارد.

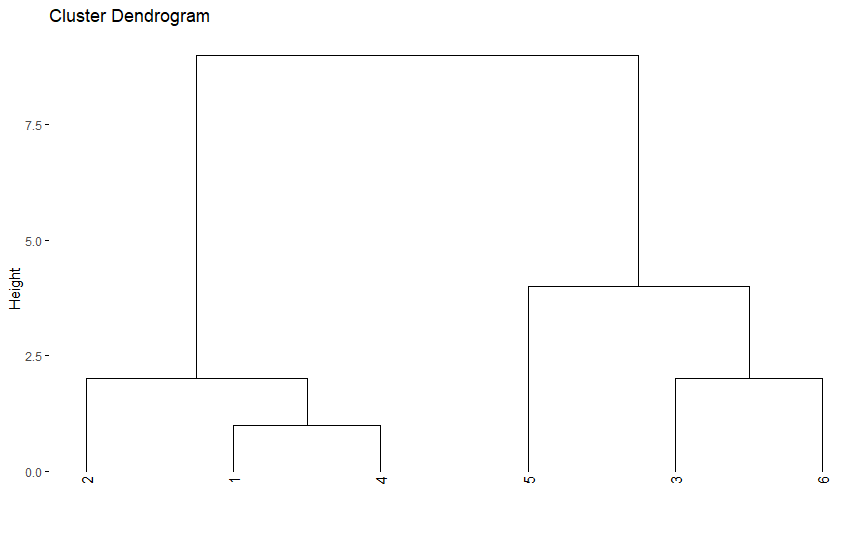
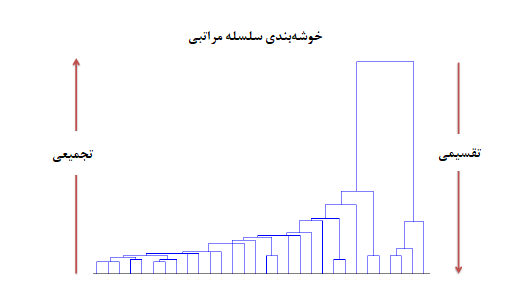
هر چند ممکن است امکان دسته‌بندی روش‌ها و الگوریتم‌ها خوشه‌بندی به راحتی میسر نباشد،‌ ولی طبقه‌بندی کردن آن‌ها درک صحیحی از روش خوشه‌بندی بکار گرفته شده در الگوریتم‌ها به ما می‌دهد. معمولا ۴ گروه اصلی برای الگوریتم‌های خوشه‌بندی وجود دارد. الگوریتم‌های خوشه‌بندی تفکیکی، الگوریتم‌های خوشه‌بندی سلسله مراتبی، الگوریتم‌های خوشه‌بندی برمبنای چگالی و الگوریتم‌های خوشه‌بندی برمبنای مدل. در ادامه به معرفی هر یک از این گروه‌ها می‌پردازیم.

خوشه‌بندی تفکیکی (Partitioning Clustering)

در این روش، براساس n‌ مشاهده و k گروه، عملیات خوشه‌بندی انجام می‌شود. به این ترتیب تعداد خوشه‌ها یا گروه‌ها از قبل در این الگوریتم مشخص است. با طی مراحل خوشه‌بندی تفکیکی، هر شیء فقط و فقط به یک خوشه تعلق خواهد داشت و هیچ خوشه‌ای بدون عضو باقی نمی‌ماند. اگر نشانگر وضعیت تعلق $x_{i}$ به خوشه $c_{j}$ باشد تنها مقدارهای ۰ یا ۱ را می‌پذیرد. در این حالت می‌نویسند:

$l_{i j} = 1, x_{i} \in c_{j} o r l_{i j} = 0, x_{i} \notin c_{j}$

هر چند این قانون‌ها زمانی که از روش «خوشه‌بندی فازی» (Fuzzy Clustering) استفاده می‌شود، تغییر کرده و برای نشان دادن تعلق هر شئی به هر خوشه از درجه عضویت استفاده می‌شود. به این ترتیب میزان عضویت $x_{i}$ به خوشه $c_{j}$ مقداری بین ۰ و ۱ است. در این حالت می‌نویسند:

$l_{i j} \in [0, 1]$

معمولا الگوریتم‌های تفکیکی بر مبنای بهینه‌سازی یک تابع هدف عمل می‌کنند. این کار براساس تکرار مراحلی از الگوریتم‌های بهینه‌سازی انجام می‌شود. در نتیجه الگوریتم‌های مختلفی بر این مبنا ایجاد شده‌اند. برای مثال الگوریتم «k-میانگین» (K-means) با تعیین تابع هدف براساس میانگین فاصله اعضای هر خوشه نسبت به میانگینشان، عمل می‌کند و به شکلی اشیاء را در خوشه‌ها قرار می‌دهد تا میانگین مجموع مربعات فاصله‌ها در خوشه‌ها، کمترین مقدار را داشته باشد. اگر مشاهدات را با x نشان دهیم، تابع هدف الگوریتم «k-میانگین» را می‌توان به صورت زیر نوشت:

$E = k \sum j = 1 \sum x \in c_{j} d i s t (x, μ_{c})$

که در آن $μ_{c j}$ میانگین خوشه‌ $c_{j}$ و dist نیز مربع فاصله اقلیدسی است.

به این ترتیب با استفاده از روش‌های مختلف بهینه‌سازی می‌توان به جواب مناسب برای خوشه‌بندی تفکیکی رسید. ولی از آنجایی که تعداد خوشه‌ها یا مراکز اولیه باید به الگوریتم داده شود، ممکن است با تغییر نقاط اولیه نتایج متفاوتی در خوشه‌بندی بدست آید. در میان الگوریتم‌های خوشه‌بندی تفکیکی، الگوریتم k-میانگین که توسط «مک‌کوئین» (McQueen) جامعه شناس و ریاضیدان در سال ۱۹۶۵ ابداع شد از محبوبیت خاصی برخوردار است.

نکته: در شیوه خوشه‌بندی تفکیکی با طی مراحل خوشه‌بندی، برچسب عضویت اشیاء به هر خوشه براساس خوشه‌های جدیدی که ایجاد می‌شوند قابل تغییر است. به این ترتیب می‌توان گفت که الگوریتم‌های خوشه‌بندی تفکیکی جزء الگوریتم‌های «یادگیری ماشین بدون ناظر» (Unsupervised Machine Learning) محسوب می‌شوند.

در تصویر ۱ نتایج ایجاد ۴ خوشه‌ روی داده‌های دو بعدی به کمک الگوریتم k-میانگین نمایش داده شده است. داشتن حالت کروی برای داده‌ها به ایجاد خوشه‌های مناسب در الگوریتم k-میانگین کمک می‌کند.

تصویر ۱- خوشه‌بندی k-میانگین برای داده‌های دو بعدی

دسامبر 9, 2019/0 دیدگاه /توسط hgadmin

خوشه بندی (Clustering) قسمت 2

آموزش عمومی پردازش تصویر و بینایی ماشین

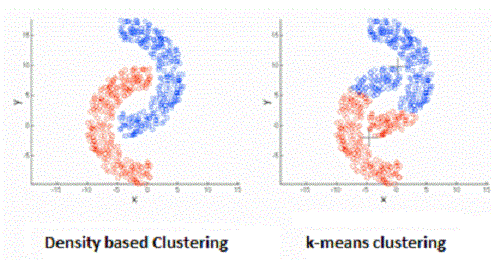
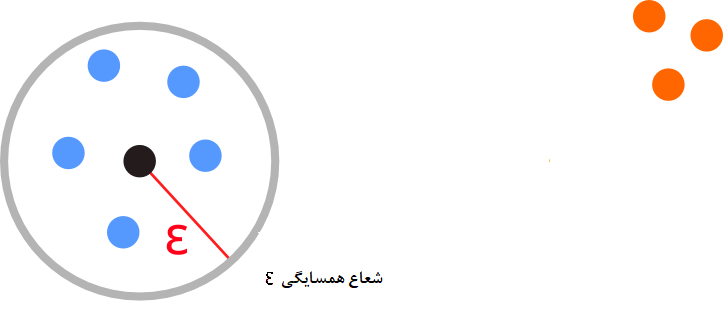
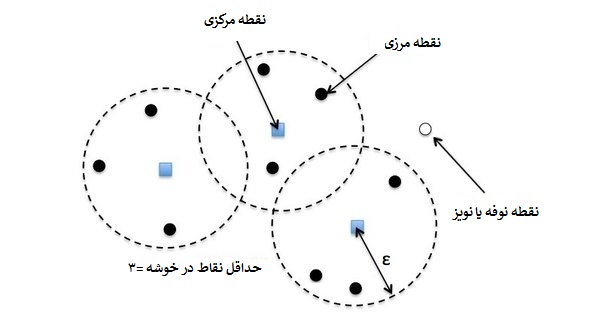
چلامارزیابی مدل خوشه‌بندی

ارزیابی (یا «اعتبار سنجی») نتایج خوشه بندی به همان اندازه خوشه بندی سخت است. رویکردهای محبوب شامل ارزیابی “درونی” است که در آن خوشه بندی به یک عدد کیفیت واحد خلاصه می‌شود، ارزیابی “خارجی”، که در آن خوشه بندی با طبقه بندی “ground truth” موجود، ارزیابی “دستی” توسط متخصص و ارزیابی “غیر مستقیم ” با استفاده از خوشه بندی در برنامه مورد نظر مقایسه می‌شود.

مشکلی که ارزیابی خارجی دارد این است که اگر ما برچسبهای “ground truth” داشته باشیم، دیگر نیازی به خوشه نخواهیم داشت و در برنامه‌های کاربردی معمولا چنین برچسب‌هایی را نداریم. از سوی دیگر، برچسب‌ها فقط یک پراکندگی از مجموعه داده نشان می‌دهد، که به این معنی نیست که خوشه ای متفاوت و شاید حتی بهتر از آن وجود نداشته باشد.

بنابراین هیچکدام از این روشها نهایتا نمیتوانند کیفیت واقعی خوشه بندی را قضاوت کنند، اما اینکار نیاز به ارزیابی انسانی دارد که بسیار ذهنی است.

ارزیابی داخلی

هنگامی که یک نتیجه خوشه بندی ای که بر اساس داده‌های خودش خوشه بندی شده‌است، ارزیابی شود، ارزیابی داخلی نامیده می‌شود.اگر از استاندارد gold استفاده شود، اندازه گیری خارجی نامیده می‌شوند و در بخش بعدی مورد بحث قرار می‌گیرد .(اگر متقارن باشد، می‌تواند اندازه گیری بین خوشه ایی برای ارزیابی داخلی استفاده شود.) روش‌ها معمولا بهترین عدد را برای الگوریتمی که درون خوشه شباهت زیاد و بین خوشه‌ها ، شباهت کم باشد،تولید می‌کند.این ارزیابی به سمت الگوریتم‌هایی است که از یک مدل خوشه ای استفاده می‌کنند. به عنوان مثال، خوشه بندي k-means به‌طور طبيعي به فضاهاي شئي بهينه مي كند و معيار داخلي مبتني بر فاصله، احتمالا از خوشه بندي به دست مي آيد.

بنابراین، اقدامات ارزیابی داخلی برای درک وضعیتی که یک الگوریتم بهتر از دیگری عمل می‌کند، مناسب است، اما این به این معنی نیست که یک الگوریتم نتیجه‌های معتبرتری را نسبت به دیگری تولید کند.

بیش از دوازده اندازه گیری ارزیابی داخلی وجود دارد. به عنوان مثال، برای ارزیابی کیفیت خوشه بندی می‌توان از روش‌های زیر استفاده کرد.

شاخص Davies–Bouldin

شاخصDavies–Bouldin را می‌توان با فرمول زیر محاسبه کرد:

$D={\frac {\min _{1\leq i<j\leq n}d(i,j)}{\max _{1\leq k\leq n}d^{\prime }(k)}}\,,$

که n تعداد خوشه و $c_{x}$ مرکز خوشه x و σx فاصله متوسط همه عناصر در خوشه x و $d(c_{i},c_{j})$ فاصله بین مرکزهای $c_{i}$ و $c_{j}$ است.از آنجا که الگوریتم‌هایی که خوشه‌ها را با فاصله‌های درونی خوشه ای کم (شباهت بین خوشه ای بالا) و فاصله‌های بین خوشه ای بالا (شباهت بین خوشه ای پایین) تولید می‌کنند، یک شاخص Davies–Bouldin پایین خواهیم داشت، الگوریتم خوشه بندی که مجموعه ای از خوشه‌های با کوچکترین شاخصDavies–Bouldin ، بهترین الگوریتم بر اساس این معیار است.

شاخصDunn

هدف شاخص Dunn شناسایی خوشه‌های متراکم و جداسازی آنهاست و به عنوان نسبت بین کمترین فاصله بین خوشه ای تا حداکثر فاصله بین خوشه ای تعریف شده‌است. برای هر قسمت خوشه، شاخص دان را می‌توان با فرمول زیر محاسبه کرد:

$D={\frac {\min _{1\leq i<j\leq n}d(i,j)}{\max _{1\leq k\leq n}d^{\prime }(k)}}\,$

که d (i، j) فاصله بین خوشه‌های i و j را نشان می‌دهد و d ‘(k) فاصله بین خوشه ایی خوشه k را اندازه گیری می‌کند. فاصله بین خوشه ای d (i، j) بین دو خوشه ممکن است هر تعداد از اندازه گیری‌های فاصله، مانند فاصله بین centroids از خوشه‌ها باشد. به‌طور مشابه، فاصله بین خوشه ای d ‘(k) ممکن است از روش‌های مختلف اندازه گیری شود، مانند فاصله حداکثر بین هر جفت المان در خوشه k.

از آنجایی که معیار داخلی به دنبال خوشه‌هایی با شباهت بین خوشه ای بالا و شباهت بین خوشه ای کم است، الگوریتم‌هایی که خوشه‌ها را با شاخص Dunn بالایی تولید می‌کنند بیشتر مطلوب است.

ضریب Silhouette

ضریب Silhouette در مقایسه با فاصله میانگین تا عناصر در خوشه‌های مشابه با میانگین فاصله تا عناصر در خوشه‌های دیگر، مقایسه می‌شود. اشیاء با Silhouette بالا به خوبی خوشه بندی می‌شوند، اشیاء باSilhouette کم ممکن است ناپایدار باشند. این شاخص با خوشه بندی k-means کار می‌کند و همچنین برای تعیین تعداد مطلوب خوشه‌ها استفاده می‌شود.

ارزیابی خارجی

در ارزیابی خارجی، نتایج خوشه بندی بر اساس داده‌هایی که برای خوشه بندی استفاده نشدند، مانند برچسب‌های کلاس شناخته شده و معیارهای خارجی ارزیابی می‌شود. چنین معیارهایی قبل از طبقه بندی اغلب توسط متخصص تعیین می‌شود. بنابراین مجموعه معیارها می‌تواند به عنوان یک استاندارد gold برای ارزیابی استفاده شود. این نوع روش‌های ارزیابی اینکه چقدر خوشه بندی به کلاس‌های معیاری پیش تعیین شده نزدیک است، را تعیین می‌کند. با این حال، اینکه آیا این برای داده‌های واقعی مناسب است یا فقط بر روی مجموعه داده‌های مصنوعی با ground truth است، مورد بحث قرار گرفته‌است ، از آنجا که کلاس‌ها می توانند ساختار داخلی داشته باشند، ویژگی‌های موجود ممکن است اجازه جدا شدن خوشه‌ها یا کلاس‌ها را ندهند.

همانند ارزیابی داخلی، چند اندازه گیری برای ارزیابی خارجی وجود دارد که در ادامه چند روش بیان شده‌است.

Purity: خلوص برای خوشه‌هایی که دارای یک کلاس واحد هستند،اندازه گیری می‌شود.برای محاسبهٔ آن ، برای هر خوشه، تعداد نقاط داده از کلاس معمول در خوشهٔ مورد نظر شمرده می‌شود ،سپس تمام خوشه‌ها را جمع شده و بر تعداد نقاط داده تقسیم می‌شود. با توجه به مجموعه ای از خوشه‌های M و برخی از مجموعه ای از کلاس‌های D، هر دو پارامتر با N نقطه داده، خلوص را می‌توان به صورت زیر تعریف کرد:

${\frac {1}{N}}\sum _{m\in M}\max _{d\in D}{|m\cap d|}$

اندازه گیری رند (ویلیام رند، 1971)

شاخص رند اینکه خوشه‌ها (که توسط الگوریتم خوشه بندی بازمی گردند) به معیار طبقه بندی‌ها چقدر شبیه‌اند را محاسبه می‌کند. همچنین می توانید شاخص رند را به عنوان اندازه گیری درصد تصمیمات درست که توسط الگوریتم ساخته شده‌است را استفاده کرد. که می‌توان با استفاده از فرمول زیر محاسبه کرد:

$RI={\frac {TP+TN}{TP+FP+FN+TN}}$

TP تعداد مثبت صحیح و TN تعداد منفی صحیح وFP تعداد مثبت کاذب وFN تعداد منفی‌های کاذب می‌باشد .

اندازه گیری F

اندازه گیری F را می‌توان برای تعادل مشارکت منفی‌های کاذب با استفاده از وزن دادن از طریق پارامتر β≥0 استفاده کرد.

$P={\frac {TP}{TP+FP}}$

$R={\frac {TP}{TP+FN}}$

که pنرخ دقت و R نرخ فراخوان است. F را با استفاده از فرمول زیر محاسبه شده‌است:

$F_{\beta }={\frac {(\beta ^{2}+1)\cdot P\cdot R}{\beta ^{2}\cdot P+R}}$

شاخص Jaccard

شاخص Jaccard برای اندازه گیری شباهت بین دو مجموعه داده استفاده می‌شود. شاخص Jaccard مقداري بين 0 و 1 دارد. شاخص 1 بدين معني است که دو مجموعه داده يکسان هستند و شاخص 0 نشان مي دهد که مجموعه داده‌ها هيچ عنصر مشترکي ندارند. شاخص Jaccard توسط فرمول زیر تعریف می‌شود:

$J(A,B)={\frac {|A\cap B|}{|A\cup B|}}={\frac {TP}{TP+FP+FN}}$

شاخص Dice

اندازه گیری متقارنDice دو برابر وزن TP است در حالی کهTN نادیده گرفته می‌شود و برابر با F1 است – اندازه گیری F با β = 1 :

$J(A,B)={\frac {|A\cap B|}{|A\cup B|}}={\frac {2TP}{2TP+FP+FN}}$

شاخص Fowlkes-Mallows (E. B. Fowlkes & C. L. Mallows 1983)

شاخص Fowlkes-Mallows شباهت میان خوشه‌های بازگشتی توسط الگوریتم خوشه بندی و معیارهای طبقه بندی را محاسبه می‌کند. هر چه مقدار شاخص Fowlkes-Mallows بیشتر باشد خوشه‌ها و معیارهای طبقه بندی مشابه هستند.این شاخص را می‌توان با استفاده از فرمول زیر محاسبه کرد:

$FM={\sqrt {{\frac {TP}{TP+FP}}\cdot {\frac {TP}{TP+FN}}}}$

کهTP تعداد مثبت واقعی وFP تعداد مثبت کاذب وFN تعداد منفی‌های کاذب است. FM شاخص میانگین هندسی دقت و فراخوانی P, R است و همچنین به عنوان اندازه گیری G شناخته شده‌است، در حالی که اندازه گیری F میانگین هارمونیک آن‌ها است. علاوه بر این، دقت و یادآوری نیز به عنوان شاخص والاس $B^{I}$ و $B^{II}$ شناخته شده‌است.

اطلاعات متقابل، اندازه گیری نظری اطلاعاتی است که چقدر اطلاعات بین خوشه بندی و طبقه بندی ground-truth است که می‌تواند تشابه غیر خطی بین دو خوشه بندی را تشخیص دهد.

ماتریسconfusion

یک ماتریس confusion می‌تواند برای به سرعت نتایج یک طبقه بندی (یا خوشه بندی) الگوریتم را نمایش دهد و نشان می‌دهد که چگونه یک خوشه از خوشه استاندارد gold متفاوت است.

تمایل خوشه

هدف از اندازه گیری تمایل خوشه،این است که چه درجه ای خوشه‌ها در داده‌های خوشه بندی شده وجود داردو ممکن است قبل از تلاش برای خوشه سازی به عنوان یک آزمون اولیه انجام شود. یکی از راه‌های انجام این کار این است که داده‌ها با دادههای تصادفی مقایسه شود. در اصل ،داده‌های تصادفی نباید خوشه ای داشته باشند.

آمار Hopkins

فرمول‌های متعدد از آمار هاپکینز وجود دارد. یک نمونه به این صورت می‌باشد که : X مجموعه ای از n نقاط داده درd بعد است. یک نمونه تصادفی (بدون جایگزینی)

m≪n با اعضای xi را در نظر بگیرید .همچنین یک مجموعه Y از m نقطه داده با توزیع یکنواخت رندوم یکنواخت تولید کنید.دو فاصله اندازه گیری، ui فاصله از yi∈Y از نزدیک‌ترین همسایه اش در X و $w_i$ فاصله ازxi∈X از نزدیک‌ترین همسایه اش در X است. آمار Hopkins به صورت زیر تعریف می‌شود:

$H={\frac {\sum _{i=1}^{m}{u_{i}^{d}}}{\sum _{i=1}^{m}{u_{i}^{d}}+\sum _{i=1}^{m}{w_{i}^{d}}}}\,$

کاربرد

زیست شناسی، زیست‌شناسی محاسباتی و بیوانفورماتیک

بوم‌شناسی گیاه و حیوانات

تجزیه و تحلیل خوشه ای برای توصیف و مقایسه مقادیر مکانی و زمانی جوامع ارگانیسم‌ها در محیط‌های ناهمگن استفاده می‌شود؛ از آن نیز در سیستماتیک گیاه برای تولید phylogenies مصنوعی یا خوشه‌های ارگانیسم (افراد) در گونه، جنس و یا سطح بالاتر که دارای تعدادی از ویژگی‌های مشترک است، استفاده می‌شود.

Transcriptomics

خوشه بندی برای ساخت گروهی از ژن‌ها با الگوی بیان مربوطه به عنوان الگوریتم خوشه بندی HCS استفاده می‌شود. اغلب این گروه‌ها حاوی عملکرد پروتئین‌های مرتبط هستند، مانند آنزیم‌ها برای یک مسیر خاص، یا ژن‌هایی که هم تنظیم می‌شوند. آزمایشات با توان بالا با استفاده از نشانگرهای ترتیبی بیان شده (ESTs) یا میکروآرایه‌های DNA می‌تواند یک ابزار قدرتمند برای حاشیه‌نویسی ژنوم، یک جنبه عمومی ژنومیک باشد.

تجزیه و تحلیل متوالی

خوشه بندی برای دسته بندی توالی‌های همولوگ به خانواده‌های ژن ،مورد استفاده قرار می‌گیرد.به‌طور کلی این مفهوم بسیار مهمی در بیوانفورماتیک و زیست‌شناسی تکاملی است.

سیستم عامل‌های ژنوتایپ با بازده بالا

الگوریتم خوشه بندی به‌طور خودکار برای تعیین ژنوتیپ‌ها استفاده می‌شود.

خوشه بندی ژنتیک انسانی

شباهت داده‌های ژنتیکی در خوشه بندی برای به دست آوردن ساختار جمعیت استفاده می‌شود.

پزشکی

تصویربرداری پزشکی

در PET، تجزیه خوشه ای می‌تواند برای تمایز بین انواع مختلف بافت در یک تصویر سه بعدی برای بسیاری از اهداف مختلف مورد استفاده قرار گیرد.

تجزیه و تحلیل فعالیت ضد میکروبی

تجزیه خوشه ای می‌تواند برای تجزیه و تحلیل الگوهای مقاومتی آنتی بیوتیکی، طبقه بندی ترکیبات ضد میکروبی مطابق با مکانیسم عمل آن ها، طبقه بندی آنتی بیوتیک‌ها بر اساس فعالیت ضد باکتری آن‌ها استفاده شود.

بخش بندی IMRT

خوشه بندی می‌تواند برای تقسیم یک نقشه فلوئنسی به مناطق مجزا برای تبدیل به زمینه‌های قابل ارائه در پرتودرمانی براساس MLC استفاده شود.

کسب و کار و بازاریابی

تحقیقات بازار

تجزیه و تحلیل خوشه ای در تحقیقات بازار به‌طور گسترده در کار با داده‌های چندمتغیره از نظرسنجی‌ها و پانل‌های آزمایش استفاده می‌شود. محققان بازار از تحلیل خوشه ای استفاده می‌کنند تا جمعیت عمومی مصرف کنندگان را به بخش‌های بازار تقسیم کنند و به درک بهتر روابط بین گروه‌های مختلف مصرف کنندگان / مشتریان بالقوه و برای استفاده در تقسیم بندی بازار، موقعیت محصول، توسعه محصول جدید و انتخاب تست بازار کمک می‌کند.

گروه بندی اقلام خرید

خوشه بندی را می‌توان برای دسته بندی تمام اقلام خرید موجود در وب به مجموعه ای از محصولات منحصر به فرد استفاده کرد. به عنوان مثال، تمام اقلام در eBay را می‌توان به محصولات منحصر به فرد گروه بندی کرد.

وب جهان گستر

تجزیه و تحلیل شبکه اجتماعی

در مطالعه شبکه‌های اجتماعی، خوشه بندی ممکن است برای تشخیص ارتباط جوامع در گروه‌های بزرگ مردم استفاده شود.

گروه بندی نتایج جستجو

در فرایند گروه بندی هوشمند از فایل‌ها و وب سایت ها، خوشه بندی ممکن است برای ایجاد یک مجموعه مناسب تر از نتایج جستجو در مقایسه با موتورهای جستجوی معمول مانند Google استفاده شود. در حال حاضر تعدادی از ابزارهای خوشه سازی مبتنی بر وب مانند Clusty وجود دارد.

بهینه سازی نقشه Slippy

در نقشه Flickr از عکس‌ها و سایر krai سایت‌ها از خوشه بندی برای کاهش تعداد نشانگرها در یک نقشه استفاده شده‌است. این باعث می‌شود که هر دو سریعتر و میزان خطای بصری را کاهش دهد.

علوم کامپیوتر

تکامل نرم افزار

خوشه بندی در تکامل نرم افزار مفید است، زیرا آن را با اصلاح قابلیت‌هایی که پراکنده شده‌است، کمک می‌کند تا خواص میراث را در کد کاهش دهد. این یک نوع بازسازی است و از این رو، راه مستقیم نگهداری پیشگیرانه است.

بخش بندی تصویر

خوشه بندی می‌تواند برای تقسیم یک تصویر دیجیتال به مناطق مشخص برای تشخیص مرز یا تشخیص شی مورد استفاده قرار گیرد.

الگوریتم‌های تکاملی

خوشه بندی ممکن است برای شناسایی nichهای مختلف در جمعیت یک الگوریتم تکاملی استفاده شود تا فرصت تولید مجد را به‌طور یکنواخت تر بین گونه‌ها یا گونه‌های در حال رشد توزیع کرد.

سیستم توصیه گر

سیستم‌های توصیه شده به منظور توصیف ایتم جدید بر اساس سلیقه کاربر طراحی شده‌اند. گاهی اوقات از الگوریتم خوشه بندی برای پیش‌بینی ترجیحات کاربر بر اساس ترجیحات دیگر کاربران در خوشه کاربر استفاده می‌کنند.

روش مارکوف مونت کارلو زنجیره ای

خوشه بندی اغلب برای تعیین مکان و تشخیص اکسترمم در توزیع هدف، مورد استفاده قرار می‌گیرد.

تشخیص ناهنجاری

ناهنجاری‌ها معمولا – به صراحت یا به‌طور ضمنی – با توجه به ساختار خوشه ای در داده‌ها تعریف می‌شود.

علوم اجتماعی

تجزیه و تحلیل جرم

از تجزیه و تحلیل خوشه ای می‌توان برای شناسایی مناطق که در آن موارد بیشتر از انواع خاصی از جرم وجود دارد استفاده شود. با شناسایی این مناطق متمایز یا “hot spot” که جرم مشابهی در طی یک دوره زمانی اتفاق افتاده است، می‌توان منابع اجرای قانون را به‌طور مؤثرتر مدیریت کرد.

داده کاوی آموزشی

به عنوان مثال، تجزیه و تحلیل خوشه ای برای شناسایی گروه‌های مدارس یا دانشجویانی با ویژگی مشابه استفاده می‌شود.

تایپولوژی ها

در داده‌های نظرسنجی، پروژه‌هایی نظیر آنچه که توسط مرکز تحقیقاتی Pew انجام شده، از تجزیه و تحلیل خوشه ای استفاده می‌کنند تا نوع‌شناسی عقاید، عادت‌ها و جمعیت شناسایی را که ممکن است در سیاست و بازاریابی سودمند باشد، شناسایی کند.

و کاربردهای دیگر

در زمینه رباتیک

الگوریتم خوشه بندی برای آگاهی موقعیت رباتیک برای ردیابی اشیاء و تشخیص خروجی‌ها در داده‌های سنسور استفاده می‌شود.

شیمی محاسباتی

به عنوان مثال، برای پیدا کردن شباهت ساختاری و غیره، به عنوان نمونه، 3000 ترکیب شیمیایی در فضای 90 شاخص توپولوژیکی ،خوشه بندی شدند.

اقلیم شناسی

برای پیدا کردن آب و هوایی و یا الگوهای فشار جو در سطح دریا مورد نظر است.

زمین‌شناسی نفت

تجزیه و تحلیل خوشه ای برای بازسازی داده‌های اصلی ازدست رفته سوراخ پایین یا منحنی‌های لگاریتمی از دست رفته به منظور بررسی خواص مخزن استفاده می‌شود.

جغرافیای فیزیکی

خوشه بندی خواص شیمیایی در مکان‌های مختلف نمونه.

منبع

خوشه بندی (Clustering) قسمت 1
خوشه بندی (Clustering) قسمت 2
خوشه بندی (Clustering) قسمت 3

دسامبر 8, 2019/0 دیدگاه /توسط hgadmin

خوشه بندی (Clustering) قسمت 1

آموزش عمومی پردازش تصویر و بینایی ماشین

در خوشه بندی، هدف تقسیم داده به گروه‌های مختلف است که با رنگ‌های مختلف در اینجا نشان داده شده‌اند.

در تجزیه و تحلیل خوشه یا خوشه بندی، گروه بندی مجموعه ای از اشیاء انجام می‌شود اینکار به این صورت است که اشیاء در یک گروه (به نام خوشه) در مقایسه با دیگر دسته‌ها (خوشه ها) مشابه تر هستند. این وظیفه اصلی داده کاوی اکتشافی است و یک روش معمول برای تجزیه و تحلیل داده‌های آماری است که در بسیاری از زمینه‌ها از جمله یادگیری ماشین، تشخیص الگو،تجزیه و تحلیل تصویر، بازیابی اطلاعات، بیوانفورماتیک، فشرده سازی داده‌ها و گرافیک کامپیوتری استفاده می‌شود.

هدف خوشه بندی

تجزیه و تحلیل خوشه ای خود یک الگوریتم خاص نیست، بلکه روند کلی است و می‌تواند توسط الگوریتم‌های مختلفی به دست آید که در درک آنچه که یک خوشه را تشکیل می دهند و نحوه کارآمدی آن‌ها را پیدا می‌کند.

اصطلاحات خوشه‌ها شامل گروه‌هایی با فاصله‌های کم بین اعضای خوشه، مناطق متراکم فضای داده، فواصل و یا توزیع‌های آماری خاص است. بنابراین خوشه بندی می‌تواند به عنوان یک مسئله بهینه سازی چند هدفه صورت گیرد. الگوریتم خوشه بندی مناسب و تنظیمات پارامتر (از جمله پارامترهایی مانند تابع فاصله مورد استفاده، آستانه تراکم یا تعداد خوشه مورد انتظار) بستگی به تنظیم مجموعه داده‌ها توسط فرد و استفاده خاص فرد از نتایج دارد. تجزیه و تحلیل خوشه ای یک روش اتوماتیک نیست، بلکه یک فرآیند تکراری از کشف دانش یا بهینه سازی چند هدفه تعاملی است که شامل آزمایش و شکست است. اغلب لازم است که داده‌های پیش پردازش شده و پارامترهای مدل اصلاح شوند تا نتیجه حاصل ، همان نتیجهٔ دلخواه باشد.

علاوه بر اصطلاحات خوشه بندی، تعدادی از اصطلاح با معانی مشابه وجود دارد، از جمله طبقه بندی خودکار، طبقه بندی عددی، روش‌شناسی و تجزیه و تحلیل توپولوژیکی. تفاوت‌های کم اغلب در نتایج استفاده می‌شود: در داده کاوی، نتیجه گروه‌ها مورد توجه هست و در طبقه بندی خودکار، قدرت تشخیصی مورد توجه است.

تجزیه و تحلیل خوشه ای در انسان‌شناسی توسط Driver و Kroeber در سال 1932 آغاز شد و در روان‌شناسی توسط زوبین در سال 1938 و رابرت تیرون در سال 1939 معرفی شد و در سال 1943 برای طبقه بندی نظریه رفتاری در روانشناسی شخصیت توسط Cattell استفاده شده‌است.

تعریف

مفهوم “خوشه” را دقیقا نمیتوان تعریف کرد،یکی از دلایلش این است که الگوریتم‌های خوشه بندی زیادی وجود دارد. همهٔ آن‌ها یک قسمت مشترک دارند و آن یک گروه از اشیاء داده است. با این حال، محققان از مدل‌های مختلف خوشه استفاده می‌کنند و برای هر یک از این مدل‌های خوشه، الگوریتم‌های مختلفی را می‌توان ارائه داد. مفهوم یک خوشه، همانطور که توسط الگوریتم‌های مختلف یافت می‌شود، به‌طور خاصی در خواص تفاوت دارند. درک این مدلهای خوشه ، کلید فهمیدن تفاوت بین الگوریتم‌های مختلف است. مدل‌های خوشه ای معمول عبارتند از:

مدل‌های متصل: به عنوان مثال، خوشه بندی سلسله مراتبی، مدل‌هایی براساس فاصله متصل را ایجاد می‌کند.
مدل‌های مرکزی: به عنوان مثال، الگوریتم k-means ، هر خوشه را با یک بردار متوسط نشان می‌دهد.
مدل‌های توزیع: خوشه‌ها با استفاده از توزیع‌های آماری، مانند توزیع نرمال چند متغیره که در الگوریتم حداکثر انتظار ، استفاده شده‌است.
مدلهای تراکم: به عنوان مثال، DBSCAN و OPTICS خوشه را به عنوان مناطق متراکم متصل در فضای داده تعریف می‌کنند.
مدل‌های زیر فضایی: در biclustering (که به عنوان خوشه مشترک یا خوشه ای دو حالت شناخته می‌شود)، خوشه‌ها با هر دو اعضای خوشه و ویژگی‌های مرتبط مدل سازی می‌شوند.
مدل‌های گروهی: برخی از الگوریتم‌ها یک مدل تصحیح شده برای نتایج خود را ارائه نمی دهند و فقط اطلاعات گروه بندی را ارائه می دهند.
مدل‌های مبتنی بر گراف: یک کلاس، یعنی یک زیر مجموعه از گره‌ها در یک گراف به طوری که هر دو گره در زیر مجموعه با یک لبه متصل می‌شود که می‌تواند به عنوان یک شکل اولیه از خوشه مورد توجه قرار گیرد.
مدل‌های عصبی: شبکه عصبی غیرقابل نظارت ، شناخته شده‌ترین نقشه خود سازمانی است و معمولا این مدل‌ها می توانند به عنوان مشابه با یک یا چند مدل فوق شامل مدل‌های زیر فضایی، زمانی که شبکه‌های عصبی یک فرم تجزیه و تحلیل مؤلفه اصلی یا مستقل تجزیه و تحلیل المان می‌باشد .

“خوشه بندی” اساسا مجموعه ای از خوشه‌ها است که معمولا شامل تمام اشیاء در مجموعه داده‌ها می‌شود. علاوه بر این، می‌توان رابطه خوشه‌ها را به یکدیگر تعریف کند، به عنوان مثال، سلسله مراتب خوشه‌های تعبیه شده در یکدیگر.

خوشه بندی را می‌توان براساس سختی تمایز به صورت زیر مشخص کرد:

خوشه بندی سخت: هر شیء متعلق به خوشه است یا نه.
خوشه بندی نرم (همچنین: خوشه فازی): هر شیء به درجه خاصی از هر خوشه متعلق است (به عنوان مثال، احتمال وابستگی به خوشه)

همچنین امکان تمایز دقیق تر وجود دارد، مثلا:

خوشه بندی جداسازی دقیق ( پارتیشن بندی): هر شیء دقیقا به یک خوشه متعلق است.
خوشه بندی جداسازی دقیق با ناپیوستگی: اشیاء می توانند به هیچ خوشه ای تعلق نداشته باشند.
خوشه بندی همپوشانی (همچنین: خوشه بندی جایگزین، خوشه بندی چندگانه): اشیاء ممکن است متعلق به بیش از یک خوشه باشد؛ معمولا خوشه‌های سخت را شامل می‌شود
خوشه بندی سلسله مراتبی: اشیایی که متعلق به خوشه فرزند هستند، متعلق به خوشه پدر و مادر هم هستند.
خوشه بندی زیر فضا: در حالی که خوشه بندی همپوشانی، که در یک زیر فضای منحصر به فرد تعریف شده ، انتظار نمی رود که خوشه‌ها با همپوشانی داشته باشند.

الگوریتم

همانطور که در بالا ذکر شد، الگوریتم‌های خوشه بندی را می‌توان بر اساس مدل خوشه ای طبقه بندی کرد. در ادامه نمونه‌های برجسته ای از الگوریتم‌های خوشه بندی بیان شده‌است، زیرا احتمالا بیش از 100 الگوریتم خوشه بندی منتشر شده وجود دارد. همه مدلها برای خوشه هایشان بیان نشده اند، بنابراین نمی توان به راحتی دسته بندی کرد.

الگوریتم خوشه بندی عینی “صحیح” وجود ندارد، اما همانطور که اشاره شد، “خوشه بندی در چشم بیننده است.” بهترین الگوریتم خوشه بندی برای یک مسئله خاص، اغلب باید به صورت تجربی انتخاب شود، مگر اینکه یک دلیل ریاضی برای ترجیح دادن یک مدل خوشه بر دیگری وجود داشته باشد. لازم به ذکر است که یک الگوریتم که برای یک نوع مدل طراحی شده‌است و در یک مجموعه داده ای که شامل تفاوت اساسی مدل است، شکست می خورد. به عنوان مثال، k-means نمیتواند خوشه‌های غیرمحدب را پیدا کند.

خوشه بندی براساس اتصال (خوشه بندی سلسله مراتبی)

خوشه بندی براساس اتصال، که همچنین به عنوان خوشه بندی سلسله مراتبی شناخته می‌شود، بر مبنای ایده اصلی اشیائی است که بیشتر مربوط به اشیای نزدیک، نسبت به اشیاء دورتر است. این الگوریتم‌ها “اشیا” را برای ایجاد “خوشه ها” بر اساس فاصله آن‌ها متصل می‌کنند. خوشه را می‌توان به طورکلی با حداکثر فاصله مورد نیاز برای اتصال قطعات خوشه توصیف کرد. در فاصله‌های مختلف، خوشه‌های متفاوتی شکل می‌گیرند که می‌تواند با استفاده از یک دندروگرام نشان داده شود، که توضیح می‌دهد که نام معمول “خوشه بندی سلسله مراتبی” از آن می آید: این الگوریتم‌ها یک پارتیشن بندی مچموعه داده را ارائه نمی دهند، بلکه یک سلسله مراتب گسترده ای از خوشه‌هایی که در فاصله‌های معینی با یکدیگر ادغام می‌شوند، ارائه میدهد. در یک دندروگرام، محور y نشان دهنده فاصله ای است که خوشه‌ها ادغام می‌کنند، در حالی که اشیا در امتداد محور x قرار می‌گیرند به طوری که خوشه‌ها با هم مخلوط نمی‌شوند.

خوشه بندی سلسله مراتبی شامل دو نوع خوشه بندی می‌باشد:

single linkage -1 این روش که به روش Bottom-Up و Agglomerative نیز معروف است روشی است که در آن ابتدا هر داده به عنوان یک خوشه در نظر گرفته می‌شود. در ادامه با به کارگیری یک الگوریتم هر بار خوشه‌های دارای ویژگی‌های نزدیک به هم با یکدیگر ادغام شده و این کار ادامه می‌یابد تا به چند خوشهٔ مجزا برسیم. مشکل این روش حساس بودن به نویز و مصرف زیاد حافظه می‌باشد.

complete linkage -2 در این روش که به روش Top-Down و Divisive نیز معروف است ابتدا تمام داده‌ها به عنوان یک خوشه در نظر گرفته شده و با به کارگیری یک الگوریتم تکرار شونده هربار داده‌ای که کمترین شباهت را با داده‌های دیگر دارد به خوشه‌های مجزا تقسیم می‌شود. این کار ادامه می‌یابد تا یک یا چند خوشه یک عضوی ایجاد شود. مشکل نویز در این روش برطرف شده‌است.

مثال هایی از خوشه linkage

خوشه بندی براساس centroid

در خوشه بندی براساس centroid، خوشه‌ها با یک بردار مرکزی نشان داده می‌شوند، که ممکن است لزوما جزء مجموعه داده نباشد. هنگامی که تعدادی از خوشه‌ها به k متصل می‌شوند، خوشه بندی k-means یک تعریف رسمی را به عنوان یک مسئله بهینه سازی ارائه می‌دهد.

روش میانگین k در عین سادگی یک روش بسیار کاربردی و پایه چند روش دیگر مثل خوشه بندی فازی و Segment-wise distributional clustering Algorithm می‌باشد.روش کار به این صورت است که ابتدا به تعداد دلخواه نقاطی به عنوان مرکز خوشه در نظر گرفته می‌شود. سپس با بررسی هر داده، آن را به نزدیک‌ترین مرکز خوشه نسبت می‌دهیم. پس از اتمام این کار با گرفتن میانگین در هر خوشه می‌توانیم مراکز خوشه و به دنبال آن خوشه‌های جدید ایجاد کنیم. (با تکرار مراحل قبل)از جمله مشکلات این روش این است که بهینگی آن وابسته به انتخاب اولیه مراکز بوده و بنابراین بهینه نیست. مشکلات دیگر آن تعیین تعداد خوشه‌ها و صفر شدن خوشه‌ها می‌باشد.

K-means دارای تعدادی خواص نظری است. اول، فضای داده را به یک ساختار معروف به یک نمودار Voronoi تقسیم می‌کند. دوم، به لحاظ مفهومی نزدیک به طبقه بندی نزدیکترین همسایه است و به همین علت در یادگیری ماشین محبوب است. سوم، می‌توان آن را به عنوان تنوع خوشه بندی براساس مدل مشاهده کرد.

مثال هایی از خوشه بندی k-means

خوشه بندی براساس توزیع

این مدل خوشه بندی که دقیقا مربوط به آمار می‌باشد، بر اساس مدل‌های توزیع است.خوشه‌ها به راحتی می توانند به عنوان اشیایی تعریف می‌شوند که به احتمال زیاد ب توزیع یکسانی دارند. یک ویژگی خوب این رویکرد این است که با نمونه برداری از اشیاء تصادفی از یک توزیع، دقیقا شبیه نحوه تولید مجموعه داده‌های مصنوعی است. مبنای نظری این روش‌ها عالی است، ولی مشکل اصلی overfitting دارند، مگر اینکه محدودیت‌ها بر پیچیدگی مدل قرار بگیرد.

یک روش شناخته شده ،مدل مخلوط گاوس (با استفاده از الگوریتم حداکثر سازی انتظار) است. مجموعه داده‌ها معمولا با یک ثابت (برای جلوگیری از overfitting) تعداد توزیع‌های گاوسی که به صورت تصادفی استفاده شده و به منظور مناسب تر کردن مجموعه داده مدل ، پارامترهای آن به‌طور تکراری بهینه شده‌است که به یک بهینه محلی همگرا می‌شود، بنابراین در طول چند اجرا ممکن است نتایج متفاوتی تولید کند. به منظور به دست آوردن خوشه بندی سخت، اشیاء اغلب به توزیع گاوسی که به احتمال زیاد متعلق به آنهاست، اختصاص داده است که برای خوشه بندی نرم، اینکار لازم نیست.خوشه بندی مبتنی بر توزیع، مدل‌های پیچیده ای را برای خوشه‌ها ایجاد می‌کند که می‌تواند همبستگی و وابستگی ویژگی را نشان دهد.

مثال های Expectation-maximization (EM)

خوشه بندی براساس Density

در این تکنیک این اصل مطرح می‌شود که خوشه‌ها مناطقی با چگالی بیشتر هستند که توسط مناطق با چگالی کمتر از هم جدا شده‌اند. یکی از مهم‌ترین الگوریتم‌ها در این زمینه الگوریتم DBSCAN است.

روش این الگوریتم به این صورت است که هر داده متعلق به یک خوشه در دسترس چگالی سایر داده‌های همان خوشه است، ولی در دسترسی چگالی سایر داده‌های خوشه‌های دیگر نیست.(چگالی داده همسایگی به مرکز داده و شعاع همسایگی دلخواه ε است)مزیت این روش این است که تعداد خوشه‌ها به صورت خودکار مشخص می‌شود. در تشخیص نویز نیز بسیار کاراست.

مثال هایی برای خوشه بندی براساس Density

پیشرفت های اخیر

در سال‌های اخیر تلاش‌های قابل توجهی در بهبود عملکرد الگوریتم‌های موجود انجام شده‌است.با توجه به نیازهای جدید به پردازش داده‌های خیلی بزرگ، تمایل به کاربرد خوشه‌های تولید شده برای عملکرد تجاری افزایش یافته‌است. این امر منجر به توسعه روش‌های پیش خوشه سازی مانند خوشه بندیcanopy می‌شود که می‌تواند داده‌های حجیم را به‌طور مؤثر پردازش کند.

برای داده‌های با ابعاد بزرگ، بسیاری از روش‌های موجود به علت ابعاد شکست خورده است، که باعث می‌شود که توابع خاص فاصله در فضاهای بزرگ بعدی مشکل ساز باشند. این باعث شد که الگوریتم‌های خوشه بندی جدید برای داده‌های با ابعاد بزرگ ، بر خوشه بندی زیر فضایی تمرکز کنند و استفاده شود.

چندین سیستم خوشه بندی مختلف مبتنی بر اطلاعات متقابل پیشنهاد شده‌است. یکی از آن ها، تغییرات اطلاعات مارینا مالگا است که یکی دیگر از خوشه بندی سلسله مراتبی را فراهم می‌کند. با استفاده از الگوریتم‌های ژنتیکی، طیف گسترده ای از تناسب توابع مختلف، از جمله اطلاعات متقابل، می‌تواند بهینه سازی شود،پیشرفت اخیر در علوم کامپیوتری و فیزیک آماری، منجر به ایجاد انواع جدیدی از الگوریتم‌های خوشه بندی شده‌است.

خوشه بندی (Clustering) قسمت 1
خوشه بندی (Clustering) قسمت 2
خوشه بندی (Clustering) قسمت 3

دسامبر 7, 2019/0 دیدگاه /توسط daliri