الگوریتم بهینهسازی دومرحلهای ازدحام ذرات
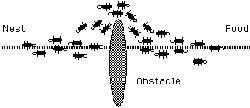
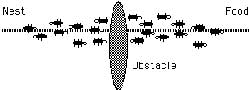
ر این مقاله روشی جدید مبتنی بر هوش جمعی برای حل مسائل بهینه سازی با روش الگوریتم بهینهسازی دومرحلهای ازدحام ذرات (particle swarm optimization algorithm) ارائه میشود. روش پیشنهادی, با استفاده از دو مرحله تحرک و همگرایی جمعیت, به نتایج جالبی در انواع توابع میرسد. در این روش جمعیت اولیه ذرات مقداردهی شده و سپس این ذرات در هر مرحله ابتدا خود را از نواحی نامناسب دور کرده و پس از آن به نواحی مناسب مهاجرت میکنند و در نهایت در این نواحی سعی در نزدیک شدن به نقاط بهینه را دارند. ویژگی الگوریتم، نتیجه گرفتن در توابع با ابعاد بالا و همچنین توابع دارای اکسترممهای محلی زیاد است. حرکت در جهت دور شدن از نواحی نامناسب، باعث میشود تا الگوریتم در مواجه با مسائل با ابعاد بسیار بزرگ و نیز مسائلی که در آنها جمعیت دارای توزیع اولیه نامناسبی است نیز به خوبی عمل کرده و نتایج مناسبی از خود نشان دهد. پراکندگی نامناسب جمعیت اولیه, در الگوریتم بهینهسازی گروه ذرات تأثیر منفی دارد. این الگوریتم با مهاجرت کلی ذرات به سمت فضای مناسب، به نقاط بهینه همگرا میشود. در انتها ضمن آزمودن روش پیشنهادی بر روی چند تابع محک شناخته شده و مقایسه با الگوریتم بهینهسازی گروه ذرات مشاهده میشود که روش پیشنهادی به نتایج بهتری میرسد.
psoیک الگوریتم رایانهای مبتنی بر جمعیت و کترهای برای حل مسئلهاست. PSOیک نوع هوش جمعی مبتنی بر اصول روانشناسی اجتماعی و فراهم آوردن بینشی در رفتار اجتماعی و کمک کردن به کاربردهای مهندسی است.
الگوریتمPSO برای اولین بار در ۱۹۷۵ توسط Kennedyو C.Eberhart توصیف شد. این تکنیکها بسیار رشد کردهاند و نسخه اصلی این الگوریتم بهطور واضحی در نسخههای امروزی قابل شناخت است. تاثیرگذاری اجتماعی و یادگیری اجتماعی یک شخص را قادر میسازد تا ثبات دانستنیهایش را برقرار سازد. انسانها مسائلشان را به کمک صحبت با دیگران و نیز به کمک برهم کنش با باورهایشان، گرایش هایشان و تغییر رفتارشان حل میکنند؛ این تغییرات را میتوان بهطور نمونه به شکل حرکت افراد به سوی یکدیگر در فضای آگاهی اجتماعی مجسم کرد.
ذرات جمعی شبیه سازی شده، این نوع از بهینهسازی اجتماعی میباشند. مسئله داه شده و چند راه برای ارزیابی مسئله پیشنهادی به ….. در شکل کلی “تابع شایستگی”حضور دارند. ساختار ارتباطی یا شبکه اجتماعی برای واگذار کردن هر همسایگی به یک فرد تعریف شده تا آن فرد با آن همسایگی بر هم کنش داشته باشد. سپس گروه کارگزاران به عنوان مهمانهای سرزده برای راه حلهای مسئله تعریف میشوند که آنها را به نام “ذرات” نیز میشناسیم؛ از این رو آنها را “ذرات دسته جمعی” نام نهادهایم.
یک فرایند تکراری برای بهبود کاندیداها در طی حرکت ذرات در نظر گرفته شدهاست. ذرات مکرراً شایستگی راه حلهای کاندیدا را ارزیابی میکنند و موقعیتی را که در آن بهترین موفقیت را داشتهاند، به خاطر می سپارند. بهره راه حل کارگزاران “بهترین ذره” یا “بهترین محل” نامیده میشود. هر ذره این اطلاعات را برای دیگر ذرات موجود در همسایگی قابل دسترسی میکند.
همچنین آنها نیز میتوانند ببینند که دیگر ذرات موجود در همسایگی در کجا بهترین موفقیت را داشتهاند.
رکتها در فضای جستجو بوسیلهٔ موفقیتهای قبلی ؛ با افرادی که بیشتر مواقع همگرایی دارند، سرانجام بهتر از حالتی است که نزدیک شدن به جواب بوسیله عواملی فاقد هوش جمعی ولی با همین روش صورت گیرد.
گروه به صورت نمونه بوسیله ذرات در فضای چند بعدی که مکان و سرعت دارد، مدل سازی میشود.
این ذرات در میان این ابر فضا(فضای دارای بیش از سه بعد) پرواز میکنند و دو توانایی ضرورری دارند:
۱-حافظهای برای ذخیرهسازی بهترین مکان خود۲-آگاهی در مورد بهترین موقعیت در همسایگی خود یا در کل فضای پاسخها اعضای دسته جمعی مکانهای خوب را به یکدیگر از طریق ارتباط انتقال میدهند و موقعیت و سرعتشان را با مکانهای خوب تنظیم میکنند.
هر ذره برای اعمال تغییری مناسب در مکان و سرعت خود اطلاعات زیر را دارا میباشد:
۱-“بهترین عمومی” که برای همه شناخته شدهاست و هنگامی که هر ذره بهترین مکان جدیدی را شناسایی کند، فوراً برای بقیه ذرات اطلاعات مربوطه را به روزرسانی میکند.
۲-“بهترین همسایگی”که ذره از طریق ارتباط با زیر مجموعههای گروه، آن را بدست میآورد.
۳-“بهترین محلی”که بهترین راه حلی است که ذره تاکنون تجربه کردهاست.
همه ذرات شروع به تأثیرپذیری از “بهترین عمومی” میکنند تا سرانجام به آن نزدیک شوند. ذرات در فضای جستجو در نزدیکی “بهترین عمومی” سیر میکنند و بقیه فضا را کاوش نمیکنند، به این پدیده”همگرایی” گفته میشود. اگر ضریب اینرسی سرعت را کوچک انتخاب کنیم، تمام ذرات میتوانند سرعتشان را کاهش دهند تا اینکه در “بهترین عمومی” به سرعت صفر نزدیکتر شوند. یک را خروج از وضعیت همگرایی اولیه(نامطلوب) این است که دوباره به موقعیت ذرات (پس از رخ دادن همگرایی)مقدار اولیه بدهیم.
منبع
الگوریتم بهینه سازی ازدحام ذرات(PSO)

مقدمه
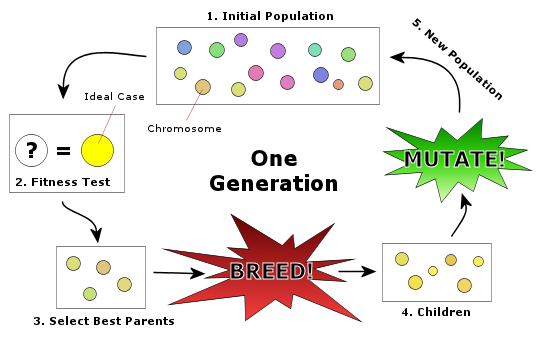
PSO(الگوریتم بهینه سازی ازدحام ذرات PSO) از دسته الگوریتم های بهینه سازی است که بر مبنای تولید تصادفی جمعیت اولیه عمل می کنند. در این الگوریتم با الگوگیری و شبیه سازی رفتار پرواز دسته جمعی (گروهی) پرندگان یا حرکت دسته جمعی (گروهی) ماهی ها بنا نهاده شده است. هر عضو در این گروه توسط بردار سرعت و بردار موقعیت در فضای جستجو تعریف می گردد. در هر تکرار زمانی، موقعیت جدید ذرات با توجه به برار سرعت و بردار موقعیت در فضای جستجو تعریف می گردد. در هر تکرار زمانی، موقعیت جدید ذرات با توجه به بردار سرعت فعلی، بهترین موقعیت یافت شده توسط آن ذره و بهترین موقعیت یافت شده توسط بهترین ذره موجود در گروه، به روز رسانی می گردد. این الگوریتم ر ابتدا برای پارامترهای پیوسته تعریف شده بود اما با توجه به اینکه در برخی از کاربردها با پارامترهای گسسته سروکار داریم، این الگوریتم به حالت گسسته نیز بست داده شده است. الگوریتم بهینه سازی ازدهام ذرات را در حالت گسسته با (BPSO) معرفی می گردد. در این الگوریتم موقعیت هر ذره با مقدار یک تعریف می گردد. در این الگوریتم موقعیت هر ذره با مقدارباینری صفر و یا یک نشان داده می شود. در BPSO مقدار هر ذره می تواند از صفر به یک و یا از یک به صفر تغییر کند. سرعت هر ذره نیز به عنوان احتمال تغییر هر ذره به مقدار یک تعریف می گردد. در این فصل بخش های مختلف این الگوریتم معرفی و بررسی خواهد شد.

تعاریف اولیه الگوریتم PSO
فرض کنید یک فضای جستجوی d بعدی داریم. i اُمین ذره در این فضای d بعدی باب بردار موقعیت Xi به شکل زیر توصیف می گردد:
بردار سرعت i اُمین ذره نیز با بردار Vi به شکل زیر تعریف می گردد:
بهترین موقعیتی که ذره i اُم پیدا کرده است را با Pi .best تعریف می کنیم:
بهترین موقعیتی که بهترین ذره در بین کل ذرات پیدا کرده است را با Pg .best به صورت زیر تعریف می کنیم:
برای به روز رسانی محل هر کدام از ذرات از رابطه زیر استفاده می کنیم:
- W : ضریب وزنی اینرسی (حرکت در مسیر خودی) که نشان دهنده میزان تأثیر بردار سرعت تکرار قبل
 بر روی بردار سرعت در تکرار فعلی
بر روی بردار سرعت در تکرار فعلی  است.
است. - c1 : ضریب ثابت آموزش (حرکت در مسیر بهترین مقدار ذره مورد بررسی)
- c2 : ضریب ثابت آموزش (حرکت در مسیر بهترین ذره یافت شده در بین کل جمعیت)
- rand1 , rand2: دو عدد تصادفی با توزیع یکنواخت در بازه 0 تا 1
- (Vi(t-1 بردار سرعت در تکرار (t-1) ام
- (Xi(t-1 بردار موقعیت در تکرار (t-1) ام
برای جلوگیری از افزایش بیش از حد سرعت حرکت یک ذره در حرکت از یک محل به محل دیگر (واگرا شدن بردار سرعت)، تغییرات سرعت را به رنج Vmin تا Vmax محدود می کنیم؛ یعنی![]() . حد بالا و پایین سرعت با توجه به نوع مسئله تعیین می گردد.
. حد بالا و پایین سرعت با توجه به نوع مسئله تعیین می گردد.
محدود سازی فضا
بعضی از مسائل دامنه تعریفی خاصی برای پارامترهای خود دارند و تنها در این دامنه دارای مقداری محدود، منطقی و تعریف شده هستند. به عبارت دیگر اگر در مسئله مورد بررسی قید و یا قیودی وجود داشته باشد، باید توسط مکانیزمی این قیود لحاظ گردند تا از ورود ذرات به فضای غیر مجاز جلوگیری شود. این مکانیزم را اصطلاحاً محدودسازی فضا می نامند. اگر از این مکانیزم ها استفاده نشود، پاسخ پیدا شه توسط الگوریتم اشتباه و یا غیر قابل اطمینان است. مثلاً تابع زیر برای مقادیر منفی x در اکثر زبان های برنامه نویسی، خطا محسوب می شود.
مکانیزمی که برای لحاظ کردن این قید استفاده می شود، بصورت زیر است:
x=max(0,x)
در تابع فوق مقادیر مجاز x؛ یعنی 0≤x بدون هیچ گونه تغییری نگاشت می شوند اما مقادیر غیر مجاز x؛ یعنی 0>x به مقدار مجاز x=0 نگاشت می شوند. در حالت کلی تر اگر بخواهیم محل ذرات بصورت ![]() باشد، برای محدودسازی می توان از رابطه زیر استفاده کرد:
باشد، برای محدودسازی می توان از رابطه زیر استفاده کرد:
با استفاده از رابطه فوق محل ذراتی که در خارج از محدوده تعریف شده قرار داشته باشند به داخل محدوده مجاز نگاشت می شوند و محل سایر ذراتی که در محدوده مجاز قرار دارند تغییری داده نمی شود.
مراحل اجرای الگوریتم PSO
بعضاً در مراجع مختلف در نحوه تفکیک مراحل اجرای الگوریتم اختلافاتی دیده می شود؛ یعنی در یک مواقع مراحل بصورت تفکیک شده تری ذکر می شوند و در برخی مواقع دو یا تعداد بیشتری از مراحل را با هم ترکیب کرده و تبدیل به یک مرحله می کنند. اما این موضوع اشکالی در برنامه نویسی های انجام شده ایجاد نمی کند زیرا آنچه که مهم است اجرا شدن مراحل برنامه به ترتیبی که در ادامه خواهد آمد، است و نحوه تفکیک این مراحل. مثلاً در برخی مراجع مرحله 4 و 5 را با هم ترکیب می کنند؛ یعنی مرحله به روز رسانی سرعت ذرات و انتقال ذرات به محل های جدید را به عنوان یک مرحله در نظر می گیرند. این تغییر اشکالی در روند اجرای الگوریتم ایجاد نخواهد کرد.
مرحله 1، تولید تصادفی جمعیت اولیه ذرات
تولید تصادفی جمعیت اولیه بطور ساده عبارت است از تعیین تصادفی محل اولیه ذرات با توزیع یکنواخت در فضای حل (فضای جستجو). مرحله تولید تصادفی جمعیت اولیه تقریباً در تمامی الگوریتم های بهینه سازی احتمالاتی وجود دارد. اما در این الگوریتم علاوه بر محل تصادفی اولیه ذرات، مقداری برای سرعت اولیه ذرات نیز اختصاص می یابد. رنج پیشنهادی اولیه برای سرعت ذرات را می توان از رابطه زیر استخراج کرد.
انتخاب تعداد ذرات اولیه
می دانیم که افزایش تعداد ذرات اولیه موجب کاهش تعداد تکرارهای لازم برای همگرا شدن الگوریتم می گردد. اما گاهی مشاهده می شود که کاربران الگوریتم های بهینه سازی تصور می کنند که این کاهش در تعداد تکرارها به معنی کاهش زمان اجرای برنامه برای رسیدن به همگرایی است، در حالی که چنین تصوری کاملاً غلط است. هرچند که افزایش تعداد ذراات اولیه کاهش تعداد تکرارها را در پی دارد. اما افزایش در تعداد ذرات باعث می گردد که الگوریتم در مرحله ارزیابی ذرات زمان بیشتری را صرف نماید که این افزایش در زمان ارزیابی باعث می شود که زمان اجرای الگوریتم تا رسیدن به همگرایی با وجود کاهش در تعداد تکرارها، کاهش نیابد. پس افزایش تعداد ذرات نمی تواند برای کاهش زمان اجرای الگوریتم مورد استفاده قرار گیرد. تصور غلط دیگری وجود دارد و آن این است که برای کاهش زمان اجرای الگوریتم می توان تعداد ذرات را کاهش داد. این تصور نیز وجود دراد و آن این است که برای کاهش زمان لازم برای ارزیابی ذرات می گردد، اما برای این که الگوریتم به جواب بهینه برسد. تعداد تکرارها افزایش می یابد. (اگر شرط همگرایی را عدم تغییر در هزینه بهترین عضو در چندین تکرار متوالی در نظر بگیریم) که در نهایت باعث می شود زمان اجرای برنامه برای رسیدن به پاسخ بهینه کاهشی نداشته باشد. همچنین باید متذکر شد که کاهش تعداد ذرات ممکن است موجب گیر افتادن در مینیم های محلی شود و الگوریتم از رسیدن به مینیمم اصلی باز ماند. اگر ما شرط همگرایی را تعدا تکرارها در نظر گرفته باشیم، هرچند با کاهش تعداد ذرات اولیه زمان اجرای الگوریتم کاهش می یابد اما جواب به دست آمده، حل بهینه ای برای مسئله نخواهد بود. زیرا الگوریتم بصورت ناقص اجرا شده است.
بطور خلاصه، تعداد جمعیت اولیه با توجه به مسئله تعیین می گردد. در حالت کلی تعداد ذرات اولیه مصالحه ای بین پارامترهای درگیر در مسئله است. بطور تجربی انتخاب جمعیت اولیه ذرات به تعداد 20 تا 30 ذره انتخاب مناسبی است که تقریباً برای تمامی مسائل تست به خوبی جواب می دهد. می توانید تعداد ذرات را کمی بیشتر از حد لازم نیز در نظر بگیرید تا کمی حاشیه ایمنی در مواجهه با مینیمم های محلی داشته باشید.
ارزیابی تابع هدف (محاسبه هزینه یا برآزندگی) ذرات
در این مرحله باید هر یک از ذرات را که نشان دهنده یک حل برای مسئله مورد بررسی است، ارزیابی کنیم. بسته به مسئله مورد بررسی، روش ارزیابی متفاوت خواهد بود. مثلاً اگر امکان تعریف یک تابع ریاضی برای هدف وجود داشته باشد، با جایگذاری پارامترهای ورودی (که از بردار موقعیت ذره استخراج شده اند) در این تابع ریاضی، به راحتی مقدار هزینه این ذره محاسبه خواهد شد. توجه داشته باشید که هر ذره حاوی اطلاعات کاملی از پارامترهای ورودی مسئله است که این اطلاعات استخراج شده و در تابع هدف قرار می گیرد.
گاهی اوقات امکان تعریف یک تابع ریاضی برای ارزیابی ذرات وجود ندارد. این حالت زمانی پیش می آید که ما الگوریتم را با یک نرم افزار دیگر لینک کرده باشیم و یا الگوریتم را برای داده های تجربی (آزمایش) استفاده می کنیم. در این گونه موارد باید اطلاعات مربوط به پارامترهای ورودی نرم افزار یا آزمایش را از بردار موقعیت ذرات استخراج کرده و در اختیار نرم افزار لینک شده با الگوریتم جایگذاری کرد و یا درآزمایش مربوطه اعمال نمود. با اجرای نرم افزار و یا انجام آزمایش و مشاهده و اندازه گیری نتایج هزینه ای را که هر یک از ذرات در پی دارند مشخص خواهد شد.
ثبت بهترین موقعیت برای هر ذره (Pi .best) و بهترین موقعیت در بین کل ذره ها (Pg .best)
در این مرحله با توجه به شماره تکرار، دو حالت قابل بررسی است:
- اگر در تکرار اول باشیم (t=1). موقعیت فعلی هر ذره را به عنوان بهترین محل یافت شده برای آن ذره در نظر می گیریم.
در سایر تکرارها مقدار هزینه به دست آمده برای ذرات در مرحله 2 را با مقدار بهترین هزینه به دست آمده برای تک تک ذرات مقایسه می کنیم. اگر این هزینه کمتر از بهترین هزینه ثبت شده برای این ذره باشد، آنگاه محل و هزینه این ذره جایگزین مقدار قبلی می گردد. در غیر این صورت تغییری در محل و هزینه ثبت شده برای این ذره ایجاد نمی شود؛ یعنی:
به روز رسانی بردار سرعت تمامی ذره ها
ضرایب w,c1, c2 با توجه به مسئله مورد نظر به روش تجربی تعیین می گردند. اما به عنوان یک قانون کلی در نظر داشته باشید که w باید کمتر از یک باشد زیرا اگر بزرگتر از یک انتخاب شود، (V(t دائماً افزایش می یابد تا جایی که واگرا گردد. همچنین توجه داشته باشید، هرچند در تئوری ضریب w می تواند منفی نیز باشد اما در استفاده عملی از این الگوریتم هیچ گاه این ضرایب را منفی در نظر نگیرید زیرا منفی بودن w موجب ایجاد نوسان در (V(t می شود. انتخاب مقدار کوچک برای این ضریب (w) نیز مشکلاتی را در پی خواهد داشت. اغلب در الگوریتم PSO مقدار این ضریب را مثبت و در رنج 0.7 تا 0.8 در نظر می گیرند. c2و c3 نیز نباید زیاد بزرگ انتخاب شوند زیرا انتخاب مقادیر بزرگ برای این دو ضریب باعث انحراف شدید ذره از مسیر خودی می شود. اغلب در الگوریتم PSO مقدار این ضرایب را مثبت و در رنج 1.5 الی 1.7 در نظر می گیرند.
لازم به یادآوری است که الزاماً مقادیر پیشنهادی فوق تنها انتخاب های ممکن برای ضرایب w,c1, c2نیست بلکه با توجه به مسئله مورد بررسی ممکن است انتخاب های بهتری غیر از موارد فوق وجود داشته باشد.
تست همگرایی
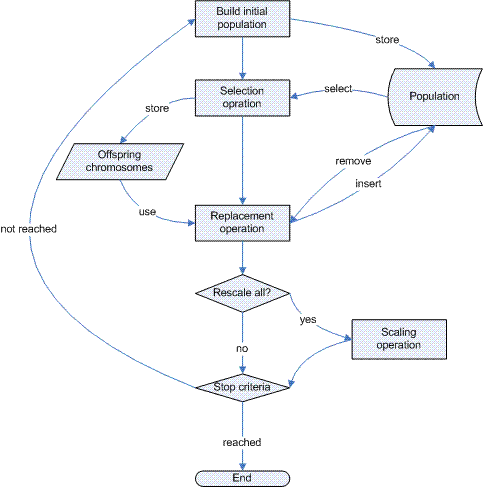
تست همگرایی در این الگوریتم مانند سایر الگوریتم های بهینه سازی است. برای بررسی الگوریتم روش های گوناگونی وجود دارد. برای مثال می توان تعداد مشخصی تکرار را از همان ابتدا معلوم کرد و در هر مرحله بررسی کرد که آیا تعداد تکرارها به مقدار تعیین شده رسیده است؟ اگر تعداد تکرارها کوچکتر از مقدار تعیین شده اولیه باشد، آن گاه باید به مرحله 2 بازگردید در غیر این صورت الگوریتم پایان می پذیرد. روش دیگری که اغلب در تست همگرایی الگوریتم استفاده می شود، این است که اگر در چند تکرار متوالی مثلاً 15 یا 20 تکرار تغییری در مقدار هزینه بهترین ذره ایجاد نگردد، آنگاه الگوریتم پایان می یابد، در غیر این صورت باید به مرحله 2 بازگردید. دیاگرام گردشی (فلوچارت) الگوریتم PSO در شکل نشان داده شده است.

فلوچارت الگوریتم pso
منبع
منابع
بهینهسازی ازدحام ذرات (PSO) قسمت 1
بهینهسازی ازدحام ذرات (PSO) قسمت 2

































.jpg)