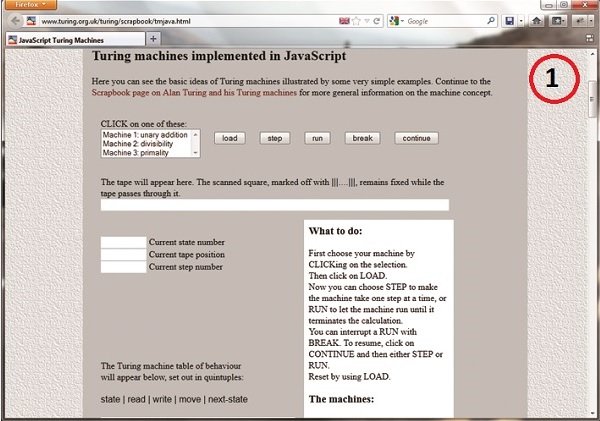
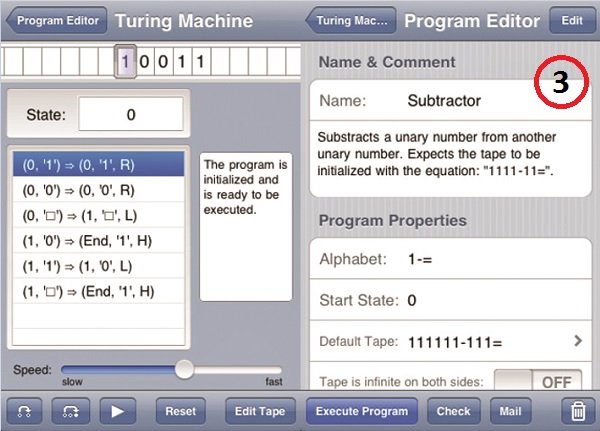
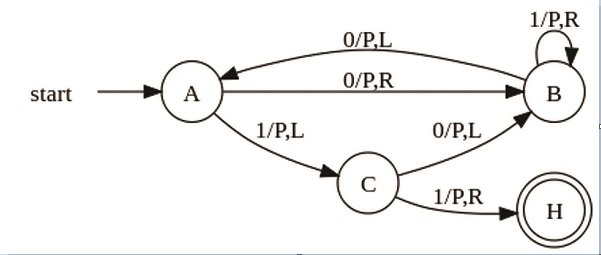
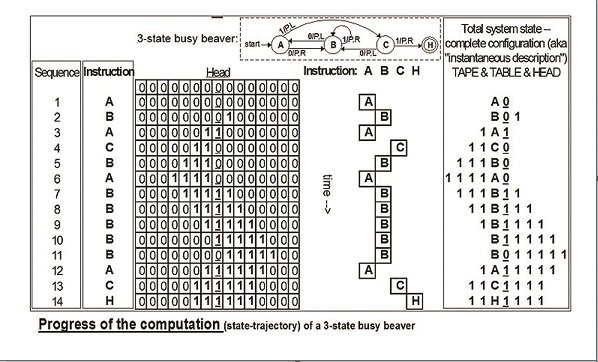
استراتژی الگوریتم های تکاملی (evolutionary strategy) (ES)
۱−۱مقدمه
الگوریتم های تکاملی(ES) یکی از روش های تکاملی می باشد. که با یک جمعیت اولیه شروع می شود در این روش بعد از انتخاب والدین از روش های تکثیر برای تولید نسل جدید استفاده می شود که در برنامه های حاضر از روش Discrete Recombination استفاده شده است. جهش نیز در یافتن مکان های جدید و جستجوی بهتر فضای جستجو کمک می کند.
۱−۲شرح الگوریتم ES
۱−۲−۱تعیین جمعیت اولیه :
ابتدا یک جمعیت اولیه در بازه مورد نظر تعیین می کنیم. این جمعیت به صورت یک ماتریس با تعداد سطر برابر با تعداد جمعیت، و تعداد ستون برابر با تعداد متغیرهای مساله می باشد.
۱−۲−۲تولید مثل Recombination:
در اینجا از روش Discrete Recombination استفاده شده است.
در این روش ابتدا دو والد را برای آمیزش در نظر می گیریم که این کار از طریق انتخاب دو عدد رندوم و در نظر گرفتن یک میزان احتمال برای انجام آمیزش صورت می گیرد.
در انتها از روش (µ+λ) یعنی افزودن تعداد فرزندان تولیدی به نسل قبل و انتخاب بهترین آنها برای نسل بعد استفاده می شود.
۱−۲−۳ جهش (mutation)
انجام این عمل ما را در رسیدن به نقطه جدید کمک می کند. اصولا جهش با اضافه نمودن یک عدد گوسی به جمعیت مورد نظر صورت می گیرد.
را می توان در هر مرحله آبدیت نمود. بدین منظور در این برنامه از روش Additive استفاده شده است که روابط آن به صورت زیر می باشد.
σij(t + 1) = σij(t) + ησij(t)Nij(0, 1)
و در نهایت جهش به صورت زیر انجام می گیرد:
۱−۲−۴ انتخاب (selection)
حال مجموعه ای از والدین و فرزندان را داریم که بهترین آنها را با توجه به مساله مورد بررسی برای تولید نسل بعد انتخاب می کنیم.
۲– برنامه ریزی تکاملی (evolutionary programming)(EP)
۲-۱ مقدمه
الگوریتم EP بسیار شبیه الگوریتم ES می باشد تنها تفاوت این دو الگوریتم در مرحله Recombination و Selection می باشد. EP دارای هیچگونه Recombination نمی باشد و اعضا تنها از طریق جهش تغییر پیدا می کنند.
۲−۲ جهش(mutation)
برای انجام این عمل از روش Additive استفاده شده است که روابط آن به صورت زیر بوده و توضیحات کامل تر آن در قسمت ES آورده شد.
σij(t + 1) = σij(t) + ησij(t)Nij(0, 1)
۲−۳ انتخاب(selection)
در الگوریتم EP برای انتخاب نسل بعد چندین روش وجود دارد که دو روش متداول ان در زیر توضیح داده شده است:
۲−۳−۱ انتخاب به روش مسابقه ای Selection Tournament
در این روش دو عضو از جمعیت موجود( مجموع جمعیت اولیه و جمعیت جهش یافته) به صورت تصادفی انتخاب شده و مقدار شایستگی آنها با هم مقایسه شده و فرد شایسته تر برای حضور در نسل بعد انتخاب می شود. در الگوریتم EP نوشته شده فرد پیروز از جمعیت اولیه خارج شده و به فرد بازنده شانس دوباره داده می شود.
۲−۳−۲ انتخاب بر اساس امتیاز Rank based Selection
در این روش نیز دو فرد از جمعیت به صورت تصادفی انتخاب می شوند و مقدار شایستگی آنها با هم مقایسه می شود. در اینجا به فرد پیروز امتیاز تعلق می گیرد. این کار چندین بار تکرار می شود تا امتیازاتی به اعضای جمعیت تعلق گیرد. حال نسل جدید بر اساس امتیازات در یافتی انتخاب می شوند.
ﻳﻚ اﻟﮕﻮرﻳﺘﻢ ﺗﻜﺎملی ﭼﻴﺴﺖ؟
اﻳﺪه اﺻﻠﻲ ﻳﻚ اﻟﮕﻮرﻳﺘﻢ ﺗﻜﺎﻣﻠﻲ ﭼﻴﺴﺖ؟
اﻳﺪه اصلی ﻳﻚ ﻣﺤﻴﻂ از ﺟﻤﻌﻴﺘﻲ از اﻓﺮاد ﺑﺎ ﻣﻨﺎﺑﻊ ﻣﺤﺪود ﺗﺸﻜﻴﻞ ﻣﻲ ﺷﻮد.
رقابت ﺑﺮاي اﻳﻦ ﻣﻨﺎﺑﻊ ﺑﺎﻋﺚ اﻧﺘﺨﺎب اﻓﺮادي ﻣﻲ ﺷﻮد ﻛﻪ ﺑﻬﺘﺮ از ﺑﻘﻴﻪ ﺑﺎ ﻣﺤﻴﻂ تطبیق یافته اﻧﺪ. این اﻓﺮاد ﺑﻪ ﻋﻨﻮان واﻟﺪ ﺑﻪ ﻣﻨﻈﻮر اﻳﺠﺎد اﻓﺮاد ﺟﺪﻳﺪ از ﻃﺮﻳﻖ آﻣﻴﺰش و ﺟﻬﺶ عمل می کنند. برازندگی افراد جدید ارزیابی می شود و سپس این افراد جدید به منظور بقاء به رقابت می پردازند. در ﻃﻮل زﻣﺎن اﻧﺘﺨﺎب ﻃﺒﻴﻌﻲ ﺑﺎﻋﺚ اﻓﺰاﻳﺶ برازندگی ﺟﻤﻌﻴﺖ ﻣﻲ ﺷﻮد.
الگوریتم های تکاملی در دسته الگوریتم های “تولید و تست” قرار می گیرند.

شمای کلی الگوریتم های تکاملی
ویژگی های الگوریتم های تکاملی:
اﻟﮕﻮرﻳﺘﻢ ﻫﺎی ﺗﻜﺎملی مبتنی ﺑﺮ ﺟﻤﻌﻴﺖ می ﺑﺎﺷﻨﺪ: ﻣﺠﻤﻮﻋﻪ ای از راه حل های کاندیدا را به طور همزمان پردازش می کنند.
الگوریتم های تکاملی اغلب از عملگر آمیزش به منظور ترکیب اطلاعات موجود در چندین راه حل در یک راه حل جدید استفاده می کنند.
3- الگوریتم های تکاملی اتفاقی(غیر قطعی) می باشند.
شبه کد یک الگوریتم تکاملی
BEGIN
INITIALISE population with random candidate solutions;
EVALUATE each candidare;
REPEAT UNTIL ( TERMINATION CONDITION is satisfied ) DO
SELECT parents;
RECOMBINE pairs of parents;
MUTATE the resulting offspring;
EVALUATE new candidates;
SELECT individuals for the next generation;
OD
END
انواع مختلف الگوریتم های تکاملی
از نظر تکنیکی، اناوع مختلف الگوریتم ها تکاملی در نحوه باز نمایی با یکدیگر تفاوت دارند:
- رشته دودویی : الگوریتم های ژنتیک
- بردارهایی از اعداد حقیقی: استراتژی های تکامل
- ماشین های متناهی الحالت: برنامه نویسی تکاملی
- درخت ها: برنامه نویسی ژنتیک
بهترین استراتژی
- انتخاب بازنمابب مناسب(طبیعی یا ساده) برای مسأله
مثال 1: حل یک مسأله ارضاء پذیری ![]() رشته های بیتی به طول n
رشته های بیتی به طول n ![]() الگوریتم ژنتیک
الگوریتم ژنتیک
مثال 2: توسعه یک برنامه کامپیوتری برای انجام بازی چکر ![]() درخت
درخت ![]() برنامه نویسی ژنتیک
برنامه نویسی ژنتیک
- انتخاب عملگرهای مناسب برای نحوه بازنمایی
- عملگرهای انتخاب تنها از مقدار برازندگی استفاده می کنند و بنابراین به بازنمایی بستگی ندارند.
مؤلفه های یک الگوریتم تکاملی
به منظور تعریف یک الگوریتم تکاملی خاص باید مؤلفه های زیر مشخص شوند:
- بازنمایی (نحوه تعریف افراد)
- تابع ارزیابی (یا تابع برازندگی)
- جمعیت
- مکانیزم انتخاب والد
- عملگرهای ژنتیکی(آمیزش و جش)
- مکانیزم انتخاب بازنده (استراتژی جایگزینی)
علاوه بر این موارد، باید نحوه تولید جمعیت اولیه و شرط (شرایط) توقف الگوریتم نیز مشخص شوند.
روش های بازنمایی(تعریف افراد)
راه حل های کاندیدا(افراد9 در فضای فنوتایپ قرار دارند. این راه حل ها به صورت کروموزوم ها کد می شوند که در فضای زنوتایپ قرار دارند.
- کد کردن: فنو تایپ
 ژنو تایپ (لزوماً یک به یک نمی باشد)
ژنو تایپ (لزوماً یک به یک نمی باشد) - دیکود کردن: ژنو تایپ
 فنو تایپ (باید یک به یک باشد)
فنو تایپ (باید یک به یک باشد)
مثالی در این زمینه می تواند، بیشینه سازی تابع ![]() در بازه ی صفر تا 15
در بازه ی صفر تا 15
کروموزوم ها حاوی ژن ها می باشند که محل قرار گرفتن زن در کروموزوم Locus و مقدار ژن Allele نام دارد.
برای یافتن بهینه سراسری، هر راه حل امکان پذیر باید بتواند در فضای ژنوتایپ بازنمایی شود.
تابع ارزیابی(برازندگی)
بیانگر نیازمندیهایی است که جکعیت باید با آنها تطبیق یابد. نوعی تابع کیفیت یا تابع هدف است و به هر فنوتایپ یک مقدار برازندگی(عدد حقیقی) نسبت می دهد و اساس انتخاب را تشکیل می دهد. بنابراین هر قدر مقادیر متفاوت تری را نسبت دهد، بهتر است. نوعاً برازندگی کمیتی است که باید بیشینه شود. تبدیل یک مسأله کمینه سازی به یک مسأله بیشینه سازی و بر عکس کار ساده ای می باشد.
جمعیت
نقش جمعیت نگهداری راه حل های ممکن برای مسأله می باشد که معمولاً دارای اندازه ثابتی می باشد و یک چندمجموعه از ژنوتایپ ها می باشد.
معمولاً عملگرهای انتخاب کل جمعیت را در نظر می گیرند، یعنی احتمال تکثیر هر کروموزوم نسبت به نسل فعلی محاسبه می شود. تعداد برازندگی ها/فنوتایپ ها/ژنوتایپ های متفاوت در جمعیت معرف تنوع آن جمعیت می باشد.
مکانیزم انتخاب
افراد را بر اساس مقدار برازندگی آنها به عنوان والد برای تولید نسل انتخاب می کند. معمولاً احتمالاتی می باشد:
- راه حل هایی که دارای کیفیت بالاتری هستند نسبت به راه حل هایی که دارای کیفیت پایین تری می باشند، شانس بیشتری برای انتخاب شدن دارند.
- اما چنین چیزی تضمین شده نیست.
- حتی بدترین فرد حاضر در جمعیت نیز شانس انتخاب شدن دارد.
همین طبیعت غیر قطعی به فرار از بهینه های محلی کمک می کند.
عملگرهای ژنتیکی
نقش آنها تولید راه حل های کاندیدای جدید می باشد. این عملگرها معمولاً بر اساس چندی(تعداد ورودی) در دو دسته قرار می گیرند:
- چندی = 1: عملگرهای جهش
- چندی> 1: عملگرهای امیزش
- چندی = 2: عملگر crossover
بحث های بسیاری در مورد اهمیت نسبی عملگرهای ژنتیکی(آمیزش و جهش) وجود دارد. امروزه اغلب الگوریتم های تکاملی از هر دو استفاده می کنند. انتخاب عملگرهای ژنتیکی خاص، وابسته به نحوه بازنمایی می باشد.
عملگر جهش
بر روی یک ژنوتایپ عمل می کند و یک ژنوتایپ جدید ایجاد می کند. در جهش، عنصر تصادفی بودن یک عنصر ضر.ری می باشد و باعث تمایز آن از دیگر عملگرهای هیوریستیک می شود. اهمیت آن بستگی به روش بازنمایی و نوع الگوریتم تکاملی دارد:
- در GA دودویی- یک عملگر پس زمینه و مسئول حفظ و ایجاد تنوع می باشد
- در EP برای ماشین های متناهی الحالت و متغیرهای پیوسته – تنها عملگر جستجو
- در GP – به ندرت استفاده می شود.
عملگر جهش می تواند تضمین کننده پیوستگی فضای جستجو باشد(اثبات همگرایی).
عملگر آمیزش
اطلاعات والدین را در فرزندان ادغام می کند. انتخاب اینکه چه اطلاعاتی باید ادغام شوند، اتفاقی می باشد. اغلب فرزندان ممکن است بدتر و یا مانند والدینشان باشند. این عملگر با این امید انجام می شود که برخی از فرزندان با ترکیب عناصر ژنوتایپ ها که منجر به ایجاد ترکیب های بهتری از ویژگی ها می شوند، از والدینشان بهتر باشند. این اصل هزاران سال توسط پرورش دهندگان گیاهان و حیوانات استفاده شده است.
جایگزینی
اغلب الگوریتم های تکاملی از یک اندازه ثابت برای جمعیت استفاده می کنند و بنابراین به روشی برای رفتن به نسل بعدی(با انتخاب افراد از میان والدین و فرزندان) نیاز دارند. اغلب قطعی می باشد :
- مبتنی بر برازندگی: مثلاً رتبه بندی والدین + فرزندان بر اساس برازندگی ها و انتخاب بهتریت ها
- مبتنی بر سن: به تعداد والدین فرزند ایجاد می شود و سپس تمامی والدین حذف می شوند.
برخی مواقع به صورت ترکیبی(elitism)
مقدار دهی جمعیت اولیه و توقف
مقدار دهی جمعیت اولیه معمولاً به صورت تصادفی می باشد. می تواند شامل راه حل های موجود باشد و یا از هیوریستسک های خاص مسأله برای ایجاد جمعیت اولیه استفاده کند. شرایط توقف در هر نسلی بررسی می شود:
- رسیدن به یک مقدار خاص از برازندگی
- رسیدن به یک حداکثر تعداد مجاز از نسل ها
- رسیدن به یک سطح حداقل از نظر تنوع
- رسیدن به یک تعداد مشخص از نسل های متوالی بدون بهبود برازندگی
الگوریتم های تکاملی در مفهوم
دیدگاه های زیادی در مرود استفاده از الگوریتم های کاملی به عنوان یک ابزار قوی در حل مسأله وجود دارد. برای اغلب مسائل یک ابزار خاص مسأله ممکن است :
- از یک الگوریتم جستجوی عمومی بر روی اغلب نمونه ها بهتر عمل کند.
- کاربرد محدودی داشته باشد
- بر روی تمام نمونه ها به خوبی عمل نکند.
هدف فراهم کردن یک ابزار قوی با عملکرد خوب بر روی گستره وسیعی از مسائل و نمونه ها می باشد.