نحوه عملکرد الگوریتم های ایمنی مصنوعی
الگوریتم های مطرح شده در سیستم های ایمنی مصنوعی را می توان به سه دسته تقسیم بندی نمود. دسته اول الگوریتم هایی که بر مبنای انتخاب جامعه سلول های B ایجاد شده اند. دسته دوم الگوریتم هایی که بر مبنای انتخاب معکوس سلول های T ایجاد شده اند. دسته سوم الگوریتم هایی که بر مبنای تئوری شبکه ایمنی بوجود آمده اند.
الگوریتم انتخاب جامعه (Clonal Selection)
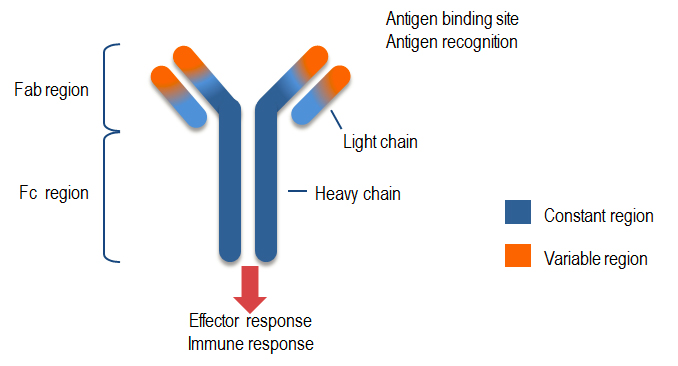
این الگوریتم بر مبنای انتخاب جامعه سلول های B ایجاد شده است.بخش های اصلی این الگوریتم شامل شناسایی آنتی ژن، تکثیر و جهش سلول های B (آنتی بادی ها) و ایجاد سلول های حافظه است. در این الگوریتم اکثر سلول ها برای تکثیر انتخاب می شوند اما از همه سلول ها به یک اندازه تکثیر نمی شوند؛ بلکه سلول هایی که میل ترکیبی بیشتری دارند ، بیشتر تکثیر می شوند.
از طرف دیگر سلول هایی که میل ترکیبی کمتری داشته اند بیشتر تغییر می یابند. به بیان دیگر تکثیر نسبت مستقیمی با میل ترکیبی و جهش نسبت عکس با میل ترکیبی دارد. بدین ترتیب میل ترکیبی سلول ها به مرور زمان افزایش یافته و تنوع نیز حفظ می شود.
مراحل الگوریتم انتخاب جامعه
مراحل الگوریتم انتخاب جامعه عبارتند از :


الگوریتم انتخاب معکوس (Negative Selection)
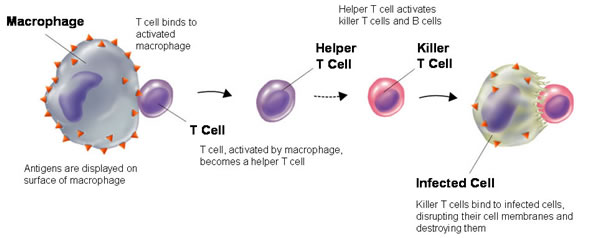
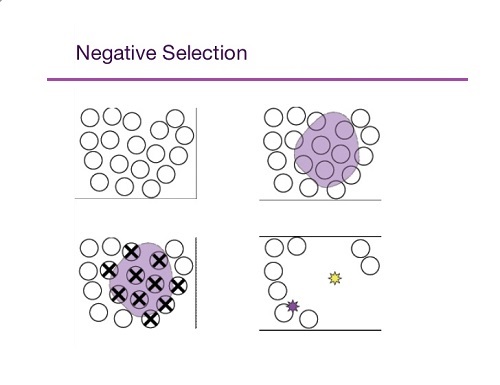
این الگوریتم بر مبنای سلول های T ایجاد شده است.سلول های T می توانند سلول های خودی و غیر خودی را از یکدیگر تشخیص دهند.الگوریتم انتخاب معکوس دو مرحله دارد. مرحله اول که مرحله یادگیری است مشابه کار تیموس را انجام می دهد. یعنی سلول هایی که سلول های خودی را شناسایی می کنند را حذف می کند. مرحله دوم، مرحله نظارت یا اجراء است. در این مرحله الگوها (آنتی ژن ها) با سلول های T باقیمانده از مرحله اول مقایسه شده و در صورت شناسایی حذف می شوند. این الگوریتم در شناسایی الگو و امنیت نظارتی کاربرد دارد.
مراحل الگوریتم انتخاب معکوس
فرض می کنیم S مجموعه الگوهای خودی باشد که باید محافظت شده و مجموعه A نیز محافظ ها می باشند.


با توجه به مراحل فوق این الگوریتم دارای قابلیت یادگیری است. پس از یادگیری از مجموعه A در مرحله نظارت یا اجراء استفاده می شود.در این مرحله هر الگوی ورودی با الگوهای جدیددر مجموعه A مقایسه می شود و در صورتی که میل ترکیبی آنها از یک حد آستانه ای بیشتر شود ، الگوی ورودی به عنوان یک الگوی غیرخودی حذف می شود.
الگوریتم شبکه ایمنی (Immune Network)
الگوریتم انتخاب جامعه دارای چند مشکل است. اول اینکه آنتی بادی های حاصل از این الگوریتم نسبت به آخرین داده های ورودی یعنی آنتی ژن ها تنظیم می شوند. دوم اینکه آنتی بادی ها تمایل دارند که در نزدیکی یکدیگر تجمع کنند.به بیان دیگر چندین آنتی بادی مقداری نزدیک به هم بدست می آورند. الگوریتم شبکه ایمنی مصنوعی این دو نقص الگوریتم انتخاب جامعه را برطرف می نماید.
در یک شبکه ایمنی مصنوعی ، برای آنتی بادی بجز میل ترکیبی با آنتی ژن ، معیارهای ارزیابی دیگری نیز وجود دارد.معیار ارزیابی اصلی در شبکه ایمنی مصنوعی میزان تحریک شدن آنتی بادی است.میزان تحریک آنتی بادی بر مبنای میل ترکیبی آنتی بادی با آنتی بادی های دیگر و میل ترکیبی سایر آنتی بادی ها با آنتی بادی مورد نظر محاسبه می شود.در صورتیکه یک آنتی بادی ، آنتی بادی دیگر یا آنتی ژن را شناسایی کند ، تحریک می شود اما از طرف دیگر شناسایی شدن یک آنتی بادی توسط آنتی بادی دیگر تاثیر بازدارندگی بر روی آن دارد. میزان تحریک یک آنتی بادی بطور کلی از رابطه زیر بدست می آید:
S = Nt – ct + Ag
Nt : میزان تحریک شدن آنتی بادی توسط شبکه است.
ct : میزان بازدارندگی شبکه ای آنتی بادی می باشد.
A : میزان تحریک آنتی بادی توسط آنتی ژن است.
به دلیل هزینه محاسباتی زیاد رابطه فوق ، الگوریتم های مختلفی برای شبکه ایمنی مصنوعی ارائه شده که از نسخه ساده شده رابطه فوق استفاده می نمایند.
مراحل الگوریتم شبکه ایمنی مصنوعی
الگوریتم شبکه ایمنی مصنوعی را می توان بطور کلی به صورت زیر تعریف کرد:


الگوریتم aiNET
الگوریتم های متفاوتی برای شبکه ایمنی مصنوعی مطرح شده است که هر یک از آنها بخش های مختلف را به روش خود تعریف کرده اند. یکی از الگوریتم های معروف؛ الگوریتم aiNET می باشد. طبق تعریف aiNET گرافی وزن دار است که ممکن است کاملا همبند نباشد. گره های این گراف را آنتی بادی ها تشکیل می دهند و وزن لبه ها نمایانگر استحکام ارتباط میان دو گره می باشد. مراحل الگوریتم aiNET عبارتند از :


مراحل ۱،۲ تا ۸،۲ در الگوریتم فوق انتخاب جامعه می باشد. در مرحله ۴،۲ جهش از رابطه ![]() بدست می آید که در آن c’ ماتریس آنتی ژن، c جامعه آنتی بادی ها و ضریب یادگیری یا نرخ جهش است. نرخ جهش در این الگوریتم از حاصل ضرب یک عدد ثابت و یک عدد تصادفی با توزیع یکنواخت در بازه صفرو یک در فاصله آنتی بادی و آنتی ژن بدست می آید.
بدست می آید که در آن c’ ماتریس آنتی ژن، c جامعه آنتی بادی ها و ضریب یادگیری یا نرخ جهش است. نرخ جهش در این الگوریتم از حاصل ضرب یک عدد ثابت و یک عدد تصادفی با توزیع یکنواخت در بازه صفرو یک در فاصله آنتی بادی و آنتی ژن بدست می آید.
در الگوریتم فوق، جامعه سازی متناسب با میل ترکیبی باعث می شود که عمل استخراج در نزدیکی پاسخ به خوبی انجام شود زیرا هرچه آنتی بادی به آنتی ژن نزدیک تر باشد، نمونه های مشابه بیشتری تولید می کند و در نتیجه عمل استخراج بهتری انجام می شود.
جهش نیز با توجه به رابطه ای که بیان شد، منتاسب با عکس میل ترکیبی است. یعنی هرچه میل ترکیبی بیشتر باشد (فاصله کمتر)، جهش ها کوچکتر می شود و عمل استخراج صورت می پذیرد و هرچه میل ترکیبی کمتر باشد (فاصله بیشتر) در نتیجه جهش های برزگتری انجام می شود. بدین ترتیب آنتی بادی هایی که از جواب دور هستند عمل اکتشاف و آنتی بادی هایی که نزدیک جواب هستند عمل استخراج را انجام خواهند داد.
مراحل ۹،۲ و ۴ به ترتیب اعمال بازدارندگی جامعه و شبکه را انجام خواهند داد. در مرحله ۹،۲ الگوریتم عمل بازدارندگی روی مجموعه اعضاء جامعه ایجاد شده برای هر آنتی زن جاری انجام می گیرد و در مرحله ۴ این عمل بر روی تمامی آنتی بادی های شبکه انجام می شود. این دو مرحله باعث می شوند آنتی بادی هایی که آنتی ژن های مشابهی را شناسایی می کنند، حذف شوند.
پارامتر حد آستانه، انعطاف پذیری شبکه، دقت خوشه بندی و میزان اختصاص بودن هر یک از آنتی بادی ها را تعیین می کند. هرچه مقدار کوچکتر باشد، آنتی بادی های شبکه می توانند به هم نزدیکتر شوند و در نتیجه دقت خوشه بندی شبکه و میزان اختصاص بودن بیشتر می شود. از طرف دیگر هرچه اتدازه بزرگتر شود، هر آنتی بادی محدوده بزرگتری را شناسایی می کند و در نتیجه شبکه از نظر حاصل از نظر تعداد آنتی بادی کوچک تر می شود و دقت خوشه بندی آن کمتر می شود.
پس از مرحله ۵ الگوریتم، خروجی شبکه به صورت مجموعه ای از آنتی بادی ها (گره های گراف) و میل ترکیبی آنها (لبه های گراف) بدست می آید که یک گراف کامل است. به منظور انجام عمل خوشه بندی، باید تعدادی از یال های گراف حذف شوند تا گراف خوشه های مختلف گراف از یکدیگر جدا شوند. برای این منظور می توان از مقدار آستانه استفاده کرد اما این روش کارایی ندارد.
در سال ۲۰۰۰ میلادی کاسترو در همایش شبکه های عصبی مصنوعی در ریودژانیروی برزیل، روش دیگری ارائه نمود. در روش کاسترو ابتدا درخت پوشای مینیمم گراف محاسبه شده و سپس یال هایی که مقدار آنها از یال های هم جوارشان به صورت مشخصی بیشتر است حذف می شوند. گره های باقیمانده به یک کلاس تعلق دارند.

معرفی انواع کاربرد سیستم های ایمنی مصنوعی
به طور کلی، سیستمهای ایمنی مصنوعی جزء الگوریتمهای الهام گرفته شده از بیولوژی هستند. این نوع الگوریتمها، الگوریتم هایی کامپیوتری هستند که اصول و ویژگیهای آنها نتیجه بررسی در خواص وفقی و مقاومت نمونهها بیولوژیکی است. سیستم ایمنی مصنوعی نوعی الگو برای یادگیری ماشین است. یادگیری ماشین، توانایی کامپیوتر برای انجام یک کار با یادگیری دادهها یا از روی تجربه است. تعریف کاسترو از سیستم ایمنی عبارتست از :
“سيستم هاي وفقي كه با الهام از ايمونولوژي نظري و توابع، اصول و مدل هاي ايمني مشاهده شده به وجود آمدهاند و برای حل مسائل مورد استفاده قرار میگیرند.”
كاسترو و تيميس سه ویژگی زیر را برای الگوريتم ايمني مصنوعي معرفی نموده اند:
۱٫ در هر الگوريتم ايمني مصنوعي، حداقل بايد يك جزء ايمني مانند لنفوسيت ها وجود داشته باشد.
۲٫ در هر الگوريتم ايمني مصنوعي بايد ايده اي برگرفته از بيولوژي نظري يا تجربي استفاده شود.
۳٫ الگوريتم ايمني مصنوعي طراحي شده بايد به حل مسئله اي كمك كند.
بر اساس سه ویژگی فوق، كاسترو و تيميس، اولين الگوريتم هاي ايمني مصنوعي را در سال ۱۹۸۶ طراحي كردند. در همان سال فارمر مدلی برای تئوری شبکه ایمنی ارائه کرد و بر اساس این مدل اعلام کرد که “سیستم ایمنی قادر به یادگیری، به خاطر سپردن و تشخیص الگوست.” بعد از نظر فارمر، توجه به سیستم ایمنی مصنوعی به عنوان یک مکانیزم یادگیری ماشین شروع شد. پس از آن به تدریج سیستم ایمنی مصنوعی ، در زمینههای مختلف وفق پذیر و جذاب بودن خود را نشان داد.
سیستم ایمنی علاوه بر توانایی تشخیص الگو، صفات دیگری از قبیل یادگیری، حافظه، خود سازماندهی و از منظر مهندسی، خصوصیات دیگری مانند تشخیص بیقاعدگی، تحمل خطا، توزیعپذیری و مقاومت بالا دارا می باشد. از زمان آغاز بحث سیستم ایمنی مصنوعی ، این سیستم برای اهداف متنوعی به کار گرفته شده است. این کاربردها را می توان تحت ۹ عنوان کاربردی دستهبندی نمود. این عناوین کاربردی عبارتند از :
۱٫ تشخیص عیب (Fault Detection)
۲٫ تشخیص ناهنجاری (Anomaly Detection)
۳٫ تشخیص نفوذ (Intrusion Detection)
۴٫ امنیت اطلاعات (Information Security)
۵٫ مسائل بهینه سازی (Optimization Problems)
۶٫ دسته بندی الگوها (Patterns Classification)
۷٫ زمانبندی (Scheduling)
۸٫ خوشه بندی (Clustering)
۹٫ سیستم های یادگیرنده (Learning Systems)
در ادامه به تشریح دو مثال از کاربردهای سیستم ایمنی مصنوعی می پردازیم.
سیستم ایمنی مصنوعی (AIS) قسمت 1
سیستم ایمنی مصنوعی (AIS) قسمت 2
سیستم ایمنی مصنوعی (AIS) قسمت 3
سیستم ایمنی مصنوعی (AIS) قسمت 4
سیستم ایمنی مصنوعی (AIS) قسمت 5
سیستم ایمنی مصنوعی (AIS) قسمت 6