معرفی سیستم ایمنی مصنوعی(Artificial Immune System)
ایمنی از مولکول ها،سلول ها و قوانینی تشکیل شده که از آسیب رساندن عواملی مانند پاتوژن ها(Pathogens) به بدن جلوگیری می کند، قسمتی از پاتوژن به نام آنتی ژن(Antigen) که توسط این سیستم قابل شناسایی و موجب فعال شدن پاسخ سیستم ایمنی می شود. یک نمونه ای از پاسخ سیستم ایمنی ترشح آنتی بادی توسط سلول های B ،که آنتی بادی ها مولکول های شناساگری به شکل Y هستند که به سطح سلول های B متصل است و با یکسری قوانین از پیش تعریف شده آنتی ژن را شناسایی می کنند. مولکول های آنتی بادی قسمتی از آنتی ژن را به نام اپیتوپ شناسایی می کنند،ناحیه ای از آنتی بادی که وظیفه شناسایی و اتصال به آنتی ژن را دارد پاراتوپ گویند که با نام V شناخته می شود، که به منظور ایجاد بیشترین میزان تطابق با آنتی ژن ها می توانند شکل خود را تغییر دهند و به همین دلیل ناحیه متغیر نامیده می شود.

سطوح سیستم ایمنی
1. اولين سطح – پوست
2. دومین سطح – ايمني فيزيولوژيکي
- اشک چشم ، بزاق دهان ، عرق و …
3. سومین سطح – ایمنی ذاتی
- پاسخ عمومی به آنتی ژن ها
- بسیار کند
4. چهارمین سطح – ایمنی اکتسابی
- پاسخ اختصاصی به آنتی ژن ها
- بسیار سریع

ایمنی ذاتی(Innate Immunity)
سیستم ایمنی ذاتی برای تشخیص و حمله تعداد کمی از مهاجمان تنظیم و برنامه ریزی شده که این سیستم پاتوژن ها را در برخورد اولیه نابود می سازد و سیستم ایمنی اکتسابی برای فعال شدن و ایجاد واکنش نیاز به وقت دارد و وظیفه سیستم ایمنی این است که به سرعت در برابر مهاجمان واکنش نشان می دهد و حمله را تحت کنترل خود قرار داده تا سیستم ایمنی اکتسابی پاسخ موثرتری را فراهم نماید، هنگامی که ایمنی ذاتی فعال می شود فقط برای چند روزی فعال می ماند.

واکنش دستگاه ایمنی ذاتی نسبت به عفونت
ایمنی اکتسابی (Adaptive Immunity)
این ایمنی هنگامی که فعال می شود برای هفته ها فعال می ماند و وظیفه ایمنی اکتسابی این است زمانی که ایمنی ذاتی به هر دلیلی کارآیی ندارد پاتوژن ها را از بین می برد. و ناکارا بودن ایمنی ذاتی یعنی اینکه نمی تواند پاسخ خاصی را برای پاتوژن مهاجم ایجاد کند و سیستم ایمنی اکتسابی وارد عمل می شود که برخلاف سیستم ایمنی ذاتی پاسخ ایمنی اکتسابی خاص و حافظه دارد و زمانی که یکبار پاتوژن به بدن حمله می کند و سیستم پاسخی را برای آن ایجاد می کند و آنرا به خاطر می سپارد و در برخورد های بعدی پاسخ سریع تری را برای مقابله با پاتوژن تولید می کند.
لنفسیت ها (Lymphocytes)
شناسایی آنتی ژن ها برعهده گلبول های سفید خون که لنفسیت نام دارد و دو نوع لنفسیت B و لنفسیت T داریم و در ادامه در مورد هر کدام توضیح خواهیم داد.
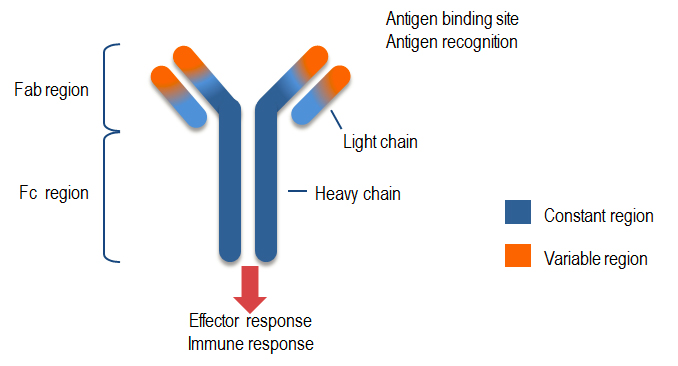
لنفسیت های نوع B
سلول های بنیادی که در مغز استخوان تولید می شوند و هر سلول B تعداد گیرنده سلولی (B-Cell Receptor) یا آنتی بادی(Antibody) در سطح خود دارد و هرکدام از این آنتی بادی ها دارای اشکال متفاوتی هستند که هر شکلی شبیه به سلول B را دارند و در نتیجه آنتی بادی هایی که توسط سلول B ساخته شده اند به مجموعه مشابهی از الگوهایی مولکولی متصل می شوند. آنتی بادی های سلول B دو ارزشی و دو عملکردی هستند، دو ارزشی به این دلیل که از طریق دو بازوی Fab به دو آنتی ژن متصل می شوند و از طریق قسمت FC به پذیرنده خاص روی سطح سلول های ایمنی دیگر وصل می شوند. اتصال به آنتی ژن دو نقش را بازی می کند که نقش اصلی آن برچسب زدن به آنتی ژن به عنوان یک مخرب تا مابقی سلول های سیستم ایمنی آن را تخریب کنند به این عملیات آماده مرگ می گویند، این کار با اتصال نواحی Fab آنتی بادی به آنتی ژن صورت می گیرد و ناحیه FC دستنخورده باقی می ماند تا اتصال با سلول های ایمنی دیگر مانند ماکروفاژها(Macrophages) صورت می پذیرد، یک آنتی بادی از دو زنجیره سبک مشابه (L) و دو زنجیره سنگین مشابه (H) تشکیل شده است که در شکل زیر نشان داده شده است.
لنفسیت های نوع T
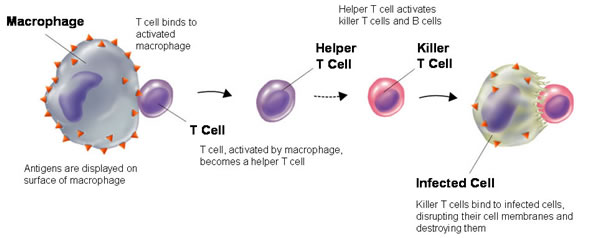
یکی از چالش های سیستم ایمنی تشخیص سلول های خودی از غیر خودی (عوامل بیماری زا) است زیرا در سطح خارجی سلول های خودی آنتی ژن وجود دارد و وظیفه سلول T تشخیص آنتی ژن های سلول های خودی که به آنها آنتی ژن خودی گفته می شود از آنتی ژن های عوامل بیماری زا که به آن آنتی ژن های غیر خودی گفته می شود. سلول های T از سلول های بنیادی مغز استخوان تولید و وارد خون می شوند سلول های T نابالغ گفته می شود که این سلول های نابالغ از طریق جریان خون وارد غده تیموس می شوند و در این غده بخشی محافظت شده وجود دارد که در آن تنها سلول های خودی وجود دارد که نمی تواند هیچ عامل بیماری زایی در بدن وجود داشته باشد.
سلول های T به چند دسته تقسیم می شوند: دسته اول سلول های T کشنده، زمانی که سلولی را شناسایی می کنند آن را از بین می برند. دسته دیگر سلول های T کمکی، آنتی بادی ها به سلول های B متصل هستند اما سلول های B آنتی ژن های خودی را از آنتی ژن های غیرخودی تشخیص نمی دهند به سلول T احتیاج دارند و پاسخ ایمنی سلول های B زمانی تولید می شود که سلول B و یک سلول T کمکی به طور همزمان یک آنتی ژن را شناسایی می کنند.
ویژگی های سیستم ایمنی بدن
سیستم ایمنی بدن شامل خصوصیاتی که بالطبع سیستم ایمنی مصنوعی از آن پیروی می کند که به صورت خلاصه در مورد هر کدام توضیح داده شده است:
1- قابلیت تشیخص الگو توسط آنتی بادی ها: این تشخیص الگو با استفاده از یک آستانه انجام می شود و زمانی که تحریک الگویی از یک آستانه بالاتر رفت به عنوان یک سلول خودی شناخته می شود.
2- تطبیقی بودن سیستم ایمنی با رخدادها و محیط: بدن انسان با محیط طبیعی خود در ارتباط است و همچنین مواد مفید یا مضر (عوامل بیماری زا) که وارد بدن انسان می شوند متغیر هستند به همین دلیل سیستم ایمنی به صورت پویا با تغییرات برخورد می کند و با وجود تغییر عوامل بیماری زا را تشخیص داده و با آنها مبارزه می کند.
3- قابلیت یادگیری: سیستم ایمنی بدن قادر است که ویروس های جدیدی را که مشاهده می کند به خاطر می سپارد.
4- همکاری گروهی: در سیستم ایمنی سلول ها به صورت گروهی، موازی و توزیع شده برای تشخیص و انهدام همکاری دارند.
5- چند لایه ای بودن: هیچ موجودیتی در سیستم ایمنی بدن انسان یک مکانیزم کامل امنیتی و دفاعی را فراهم نمی کند بلکه هر لایه سیستم ایمنی به صورت مستقل عمل کرده و با بقیه لایه ها در ارتباط است.
6- تنوع و گوناگونی: سیستم ایمنی بدن در برابر انواع مختلفی از نفوذها مقاومت کرده و تسلیم نمی شود.
7- بهینه بودن منابع: در سیستم ایمنی با ایجاد مرگ سلولی و تکثیر سلولی، یک نمونه فضای کوچکی از فضای جستجوی آنتی ژن ها در هر زمان نگه داری می کنند.
8- پاسخ انتخابی: در سیستم ایمنی بدن پس از شناسایی یک آنتی ژن پاسخ های متفاوتی داده می شود که به یک شکل عمل نمی کنند.
9- تنظیم تعداد سلول های ایمنی توسط سیستم ایمنی
سیستم ایمنی مصنوعی
یک الگویی برای یادگیری ماشین است و یادگیری ماشین یعنی توانایی کامپیوتر برای انجام یک کار با یادگیری داده ها از روی تجربه است.
کاربردهای سیستم ایمنی مصنوعی
AIS یکی از الگوریتم های الهام گرفته از سیستم ایمنی بدن انسان است و راه حل هایی را برای مسائل پیچیده ارائه داده اند و از جمله کاربردهای آن عبارتند از:
خوشه بندی (Clustering)
زمانبندی (Scheduling)
تشخیص عیب (Fault Detection)
تشخیص ناهنجاری (َAnomaly Detection)
امنیت اطلاعات (Security Infrmation)
مسائل بهینه سازی (Optimization problems)
دسته بندی الگوها (Patterns Classification)
سیستم های یادگیرنده (Learning system)
تشخیص نفوذ (Intrusion Detection)
مراحل سیستم ایمنی مصنوعی
برای حل مساله با استفاده از AIS باید 3 مرحله زیر انجام پذیرد:
1- نحوه نمایش داده های مساله (تعریف فضای شکل)
2- معیار اندازه گیری میل ترکیبی
3-انتخاب یک الگوریتم ایمنی مصنوعی برای حل مساله
فضای شکل (Shape Space)
سیستم ایمنی بر مبنای شناسایی الگو یا شناسایی شکل آنتی ژن است و می توان این سیسستم را فضایی مملوء از اشکال مختلف تشبیه کرد و هدف پیدا کردن مکمل اشکال و در نتیجه شناسایی آنها است، یعنی پیدا کردن تعدادی شکل بهینه یا آنتی بادی در فضای شکل که مکمل تمامی شکل های موجود در داده های مسئله آنتی ژن است. آنتی ژن ها به صورت آرایه ای از اعداد نمایش داده می شود و هر شیوه های که برای نمایش آنتی ژن استفاده می شود برای نمایش آنتی بادی هم نیز استفاده می شود (نحوه نمایش آنتی بادی و آنتی ژن یکسان است).
نحوه محاسبه و میل ترکیبی آنتی بادی با آنتی ژن
هر چه آنتی بادی میل ترکیبی بیشتری با آنتی ژن داشته باشد یعنی هر چه فاصله آنتی بادی و آنتی ژن کمتر شود مکمل بهتری برای آنتی ژن است و میل ترکیبی را می توان به صورت شباهت آرایه ها در نظر گرفت. که بر همین اساس در الگوریتم AIS از فاصله به عنوان معیار ارزیابی خوب یا بد بودن یک آنتی بادی استفاده می شود.
الگوریتم های AIS
الگوریتم های AIS به 3 دسته تقسیم می شوند:
1- دسته اول الگوریتم هایی که بر مبنای انتخاب کلونی سلول های B ایجاد شده اند.
2- دسته دوم الگوریتم هایی که بر مبنای انتخاب معکوس سلول های T ایجاد شده اند.
3- دسته سوم بر مبنای تئوری شبکه ایمنی ایجاد شده اند.
انتخاب کلونی (Clonal Selection)
زمانی که سلول B آنتی ژن را شناسایی می کند و سلول های B شروع به تکثیر شدن می کنند و تعداد زیادی سلول B یکسان و مشابه تولید می شود، 12 ساعت طول می کشد که یک سلول B رشد کرده و به دو سلول تبدیل شود و بعد از تحریک شدن دوره تکثیر حدودا یک هفته طول می کشد و از یک سلول 2 به توان 14 (16000) سلول مشابه تولید می شود و هر چه میل پیوندی بین سلول B و آنتی ژن بیشتر شود نرخ تکثیر بیشتر خواهد شد، در نتیجه سلول های B با میل پیوندی بالاتر، کلونی بیشتری تولید می کنند که اصل انتخاب کلونی نام دارد.
اصل انتخاب کلونی در AIS الگوریتم خاص خودش را دارد که بعد از تکثیر شدن سلول های B شروع به بالغ شدن می کنند که این فرایند در 3 مرحله صورت می پذیرد:
1- دگرگونی ایزوتایپ
2- بلوغ میل پیوندی
3- تصمیم گیری بین حافظه یا پلاسما شدن سلول B
AIS با دگرگونی ایزوتوپ در گیر نیست ولی دو مرحله بعدی در AIS مهم می باشند. ابرجهش سومانیک قسمتی از بلوغ میل پیوندی که قسمت مهمی در AIS بشمار می آید و جهش میل پیوندی آنتی بادی را می تواند کاهش یا افزایش می دهد.
سلول B در صورتی که به تکثیر ادامه می دهد که جهش باعث افزابش میل پیوندی شده باشد و آنتی بادی به طور مداوم توسط آنتی ژن تحریک می شود و تلاش برای ایجاد سلول های B بهتری دارد که فرایند بلوغ پیوندی نام دارد.گام بعدی فرایند بلوغ پیوندی انتخاب بین حافظه یا پلاسما شدن سلول B است که سلول های پلاسما سازندگان آنتی بادی هستند و در حجم زیادی آنتی بادی ترشح می کنند و عمر زیادی ندارند و حالت دیگر تبدیل سلول های B به سلول های حافظه که این سلول ها میل پیوندی زیادی با آنتی ژن دارند و هدف بخاطر سپردن این آنتی ژن برای آینده است. سلول های حافظه علاوه بر تنظیم شدن به یک نوع خاص آنتی ژن، در آینده هم برای فعال شدن نیاز به تحریک شدن کمتری دارند و در نتیجه سرعت و کارآیی پاسخ ایمنی را زمانی که پاتوژن برای بار دوم به بدن حمله می کند زیاد می شود.

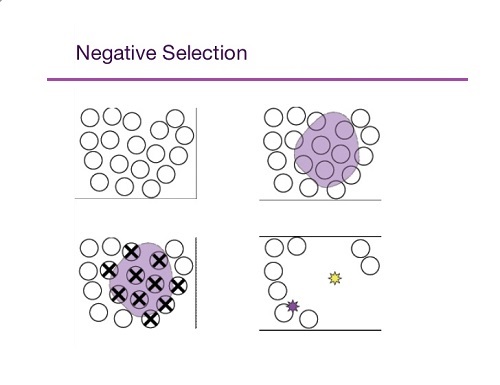
انتخاب معکوس (Negative Selection)
میل ترکیبی سلول های T نابالغ با سلول های موجود در تیموس بررسی می شود و هرکدام از سلول های T نابالغ میل ترکیبی زیادی با یکی از سلول ها داشته باشند حذف می شوند و سایر سلول های T وارد جریان خون می شوند که به این گونه انتخاب در آن برای حدف شدن انتخاب می شود انتخاب معکوس گویند.
تئوری شبکه ایمنی (Immune Network Theory)
آنتی بادی های موجود بر روی B-Cell ها می توانندعلاوه بر تشخیص آنتی ژن، آنتی بادی را هم می توانند تشخیص بدهند و باعث می شود سیستم ایمنی رفتاری پویا داشته که از آن در AIS استفاده می شود، و بر اساس این تئوری هر آنتی بادی قسمتی به نام ایدوتوپ دارد که توسط آنتی بادی دیگر قابل شناسایی است که در نتیجه آنتی بادی ها با شناسایی کردن یکدیگر سیگنال هایی را ارسال می کنند که می توانند یکدیگر را تحریک کنند و بدین ترتیب این شناسائی و تاثیر گذاری بر روی یکدیگر باعث پویایی شبکه ایمنی مصنوعی می شود. به مجموعه آنتی بادی ها که یکدیگر را شناسایی می کنند شبکه ایمنی یا ایدوتوپی گفنه می شود.

در هر الگوریتم AIS باید به 3 نکته توجه داشت:
1- در هر الگوریتم AIS باید حداقل یک جزء ایمنی مانند لنفسیت باشد.
2- در هر الگوریتم AIS باید ایده ای برگرفته از بیولوژی نظری یا تجربی باشد.
3- الگوریتم AIS که طراحی می شود باید به حل مسئله کمک کند.
مقایسه سیستم ایمنی طبیعی و الگوریتم های ایمنی مصنوعی

برگرفته از پایان نامه بنت الهدی حلمی – دانشگاه علم و صنعت – تحت عنوان استخراج قوانین انجمنی با استفاده از سیستم ایمنی مصنوعی
استخراج قوانین انجمنی با استفاده از سیستم ایمنی مصنوعی
2.برگرفته از مقاله سید امیر احسانی ، امیر مسعود افتخاری مقدم – دانشگاه آزاد اسلامی واحد قزوین – تحت عنوان کاهش معناگری داده با استفاده از سیستم های ایمنی مصنوعی
کاهش معناگری داده با استفاده از سیستم های ایمنی مصنوعی







































![{\displaystyle \min _{\mathbf {w} ,b,{\boldsymbol {\alpha }}}\{{\frac {1}{2}}\|\mathbf {w} \|^{2}-\sum _{i=1}^{n}{\alpha _{i}[y_{i}(\mathbf {w} \cdot \mathbf {x_{i}} -b)-1]}\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b140ef307512ccbafd34429bf40ee6523eac03a)


![{\displaystyle \min _{\mathbf {w} ,b}\max _{\boldsymbol {\alpha }}\{{\frac {1}{2}}\|\mathbf {w} \|^{2}-\sum _{i=1}^{n}{\alpha _{i}[y_{i}(\mathbf {w} \cdot \mathbf {x_{i}} -b)-1]}\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c411ce7bd4a910dba7b0a5a0ee3191146665dec1)


























