مسئله کوله پشتی قسمت 1

مسئله ی کوله پشتی

مسئله کوله پشتی که با عنوان‌های Knapsack یا Rucksack مطرح می‌شود، مسئله‌ای در بهینه‌سازی ترکیبیاتی است. فرض کنید مجموعه‌ای از اشیا، که هر کدام داری وزن و ارزش خاصی هستند در اختیار دارید. به هر شی تعدادی را تخصیص دهید به‌طوری‌که وزن اشیا انتخاب شده کوچکتر یا مساوی حدی از پیش تعیین شده، و ارزش آن‌ها بیشینه شود. علت نامگذاری این مسئله، جهانگردی است که کوله پشتی ای با اندازهٔ محدود دارد و باید آن را با مفیدترین صورت ممکن از اشیا پر کند.

معمولاً در تخصیص منابع با محدودیت‌های مالی، با این مسئله روبرو هستیم. همچنین مسائلی از این قبیل در ترکیبیات، نظریه پیچیدگی محاسباتی،رمزنگاری و ریاضیات کاربردی به چشم می‌خورد.

نسخهٔ مسئله تصمیم برای مسئلهٔ کوله پشتی، این سؤال است: “آیا ارزش V با انتخاب اشیایی با مجموع وزن کمتر یا مساوی W، قابل دستیابی است؟”

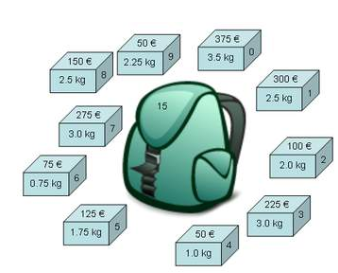
نمونه‌ای از مسئلهٔ کوله پشتی یک بعدی: چه جعبه‌هایی باید انتخاب شوند تا مقدار پول بیشینه شود اما وزن جعبه‌های مذکور بیشتر از ۱۵ کیلوگرم نشود؟ یک مسئله چند محدودیتی، می‌تواند هم وزن و هم حجم جعبه‌ها را در نظر بگیرد. مدل‌سازی اندازه و شکل جعبه‌ها، یک مسئله بسته‌بندی است.
(راه حل: اگر هر تعداد دلخواهی از جعبه‌ها در دسترس باشد، ۳ جعبهٔ زرد و ۳ جعبهٔ خاکستری پاسخ‌اند. اما اگر مطابق شکل باشد، یعنی از هر جعبه فقط یکی داشته باشیم، تمامی جعبه‌ها به جز جعبهٔ سبز را انتخاب می‌کنیم)

تعریف

مسئله کوله پشتی چیست؟ فرض کنید که جهانگردی می‌خواهدکوله پشتی خود را با انتخاب حالتهای ممکن از بین وسائل گوناگونی که بیشترین راحتی را برایش فراهم می‌سازند پر کند. این مسئله می‌تواند با شماره‌گذاری این وسائل از ۱ تا n و تعریف برداری از متغیرهای دودویی(Binary) (j = ۱٬۲,۳…n) به صورت ریاضی فرمول بندی شود. به این معنی که: اگر شیء j ام انتخاب شود در غیر اینصورت وقتی میزان راحتی باشد که وسیله j ا م فراهم می‌آورد و وزن آن و c اندازه کوله پشتی باشد. مسئله ما انتخاب برداری از بین بردارهای دودویی x است، که محدودیت را برآورده کند. بطوری‌که تابع هدف ماکزیمم مقدار خود را بگیرد به عنوان نمونه‌ای از مسائلی که می‌توانند به صورت مسئله کوله پشتی فرمول بندی شوند، مسئله زیر را در نظر بگیرید: فرض کنید که شما مایل به سرمایه‌گذاری همه یا قسمتی ازسرمایه‌تان باشید. اگر مبلغی که برای سرمایه‌گذاری در نظر گرفتید c دلار باشد و n مورد برای سرمایه‌گذاری ممکن باشد، اجازه دهیدکه سود حاصل از سرمایه‌گذاری j ام و مقدار دلارهایی باشد که آن سرمایه‌گذاری لازم دارد. بدین ترتیب جواب بهینه مسئله کوله پشتی که تعریف کردیم به ما این امکان را می دهدکه بهترین حالت ممکن را از بین حالتهای مختلف سرمایه‌گذاری انتخاب کنیم. در این رابطه باید روشی برای حل این مسئله پیدا کرد. یک روش ابتدایی که در نگاه اول توجه ما را به خود جلب می‌کند، عبارت از برنامه‌نویسی برای کامپیوتر به منظور امتحان کردن تمامی بردارهای دودویی ممکن x است، تا از بین بردارهایی که محدودیت مسئله را ارضاء می‌کنند بهترین را انتخاب کند. متأسفانه تعداد چنین بردارهایی است. بطوری‌که یک کامپیوتر فرضی که می‌تواند یک بیلیون بردار را در یک ثانیه امتحان کند؛ برای n = ۶۰ بیش از ۳۰ سال وقت لازم دارد و بیش از ۶۰ سال برای n = ۶۱ و ده‌ها قرن برای n = ۶۵ والی آخر. با این وجود، با استفاده از الگوریتمهایی خاص می‌توان در بسیاری موارد مسئله‌ای با n = ۱۰۰ ۰۰۰ را در عرض چند ثانیه روی یک کامپیوتر کوچک حل کرد __________________

فرض کنید n جسم داریم که از 1 تا n شماره‌گذاری شده‌اند. جسم {\displaystyle i} ام ارزشی معادل {\displaystyle v_{i}}و وزنی برابر با w_i دارد. معمولاً فرض می‌شود که وزن‌ها و ارزش‌ها نامنفی‌اند. برای ساده‌تر شدن نمایش، بدون کم شدن از کلیت مسئله می‌توان فرض کرد اشیا به ترتیب صعودی بر حسب وزنشان مرتب شده‌اند. بیشترین وزنی که می‌توان در کوله پشتی حمل کرد،W است.

معروف‌ترین نوع از این مسئله، مسئلهٔ کوله پشتی ۰ و ۱ است. یعنی تعداد از هر شی، یا ۰ است (آن شی را انتخاب نمی‌کنیم) یا ۱ (آن شی انتخاب می‌شود). مسئلهٔ کوله پشتی ۰ و ۱ را می‌توان به این صورت، به زبان ریاضی بیان کرد:

  • مقدار {\displaystyle \qquad \sum _{i=1}^{n}v_{i}x_{i}} را بیشینه کنید.
  • به‌طوری‌که {\displaystyle \qquad \sum _{i=1}^{n}w_{i}x_{i}\leqslant W,\quad x_{i}\in \{0,1\}}

مسئلهٔ کوله پشتی کران دار، نسخهٔ دیگری از این سؤال است که در آن تعداد اشیا (x_i) عددی صحیح و نامنفی و حد اکثر برابر با{\displaystyle c_{i}} است. به بیان ریاضی:

  • مقدار {\displaystyle \qquad \sum _{i=1}^{n}v_{i}x_{i}}را بیشینه کنید.
  • به‌طوری که{\displaystyle \qquad \sum _{i=1}^{n}w_{i}x_{i}\leqslant W,\quad x_{i}\in \{0,1,\ldots ,c_{i}\}}

مسئلهٔ کوله پشتی بیکران (UKP)، هیچ محدودیتی روی تعداد اشیا قائل نمی‌شود. یعنی از هر شی، به هر تعداد دلخواهی می‌توان انتخاب کرد. نسخه‌ای ازین سؤال که بیش از همه مورد توجه قرار می‌گیرد، دارای ویژگی‌های زیر است:

  • یک مسئله تصمیم است.
  • مسئله ۰ و ۱ است.
  • برای هر شی، وزن و ارزش آن برابرند. یعنی{\displaystyle w_{i}=v_{i}}.

دقت کنید که در این مورد خاص، این مسئله هم ارز است با: ” مجموعه‌ای از اعداد صحیح نا منفی داده شده‌است. آیا زیر مجموعه‌ای از آن وجود دارد که جمع اعضایش دقیقاً W شود؟” و چنانچه وزن‌های منفی هم قابل قبول باشند، و W برابر با {\displaystyle 0} در نظر گرفته شود، مسئله عبارت است از: ” مجموعه‌ای از اعداد صحیح داده شده‌است. آیا زیر مجموعه‌ای غیر تهی از آن هست که جمع اعضایش {\displaystyle 0} شود؟” این مسئله خاص، مسئله جمع زیرمجموعه‌ها نامیده می‌شود. در رمزنگاری، هر گاه از مسئله کوله پشتی نام برده می‌شود، منظور مسئله جمع زیرمجموعه‌ها است.

چنانچه چند کوله پشتی داشته باشیم، مسئله تبدیل به سؤال bin packing می‌شود.

پیچیدگی محاسباتی

از دید علوم کامپیوتر، مسئلهٔ کوله پشتی شایان توجه است زیرا:

  • الگوریتمی با زمان اجرای شبه چندجمله‌ای با استفاده از برنامه‌نویسی پویا دارد.
  • الگوریتمی تقریبی با زمان چندجمله‌ای دارد که از الگوریتم‌های با زمان شبه چندجمله‌ای به عنوان یک زیر-برنامه استفاده می‌کند.
  • حل دقیق این سؤال، مسئله‌ای از نوع NP-complete است؛ بنابراین پیش‌بینی شده که راه حلی که هم درست و هم سریع باشد (با زمان اجرای چندجمله‌ای) برای هر ورودی دلخواه، ندارد.

مسئله جمع زیر مجموعه‌ها که نسخه‌ای از مسئلهٔ کلی کوله پشتی است، به عنوان یکی از 21 مسئلهٔ NP-کاملِ Karp مطرح است.

تلاش‌هایی برای استفاده از مسئلهٔ جمع زیر مجموعه‌ها به عنوان اصل در سیستم‌های رمزنگاری کلید عمومی، مانند سیستم رمزنگاری کوله پشتی مرکل-هلمن انجام شد. در این روش‌ها، معمولاً ازگروه‌هایی به جز اعداد صحیح استفاده می‌شد. Merkle-Hellman و الگوریتم‌های مشابه دیگر بعداً با شکست روبرو شدند، زیرا مسائل خاصی که تولید می‌کردند در زمان چندجمله‌ای قابل حل بودند.

در خیلی از تحقیقات سعی می‌شود به این سؤال پاسخ داده شود که نمونه‌های سخت مسئلهٔ کوله پشتی چه هستند؟ یا از دید دیگر، چه ویژگی‌هایی از مثال‌های مسئلهٔ کوله پشتی، باعث می‌شود در زمانی معقولتر نسبت به آنچه در صورت کلی NP-completeِ سؤال مطرح است، حل شوند. . الگوریتم‌های زیادی بر پایه ی: برنامه‌نویسی پویا، روش تقسیم و حد، یا ترکیبی از هر دو روش برای این مسئله وجود دارند.

راه حل برنامه‌نویسی پویا

مسئلهٔ کوله پشتی بیکران

اگر تمام وزن‌ها ({\displaystyle w_{1},\ldots ,w_{n},W}) اعداد صحیح نامنفی باشند، مسئلهٔ کوله پشتی در زمانی شبه چندجمله‌ای با استفاده از برنامه‌نویسی پویا قابل حل است.

برای سادگی فرض کنید تمام وزن‌ها اکیداً مثبت اند ({\displaystyle w_{i}>0}). می‌خواهیم جمع ارزش کالاهای انتخاب شده را بیشینه کنیم با این فرض که مجموع وزن آن‌ها حداکثر{\displaystyle W} شود. حال برای هر {\displaystyle w<W}، مقدار {\displaystyle m[w]} را بیشترین ارزش قابل دستیابی تعریف کنید به‌طوری‌که جمع وزن اشیا انتخاب شده حد اکثر w شود. بدیهی است که {\displaystyle m[W]} پاسخ مورد نظر است.

دقت کنید که {\displaystyle m[w]} ویژگی‌های زیر را دارد:

  • {\displaystyle m[0]=0\,\!} (جمع اعضای مجموعهٔ تهی ۰ است)
  • {\displaystyle m[w]=\max _{w_{i}\leq w}(v_{i}+m[w-w_{i}])} که {\displaystyle v_{i}} ارزش شی i ام است.

بیشترین ارزش قابل دستیابی از مجموعهٔ تهی، ۰ است. برای محاسبهٔ هر کدام از {\displaystyle m[w]}‌ها، باید n شی را بررسی کرد. همچنین آرایهٔ W، m عنصر دارد. بنابراین زمان اجرای این الگوریتم {\displaystyle O(nW)}است. بدیهی است با تقسیم کردن {\displaystyle w_{1},\,w_{2},\,\ldots ,\,w_{n},\,W} بر بزرگترین مقسوم علیه مشترک شان، می‌توان زمان اجرای الگوریتم را بهینه کرد.

پیچیدگی زمانی {\displaystyle O(nW)} تناقضی با NP-complete بودن مسئلهٔ کوله پشتی ندارد. زیرا W برخلاف n، برحسب ورودی چندجمله‌ای نیست. طول W ِ ورودی، متناسب با تعداد بیت‌های لازم برای نمایش W، یعنی {\displaystyle \log W} است، نه خود {\displaystyle W}.

مسئلهٔ کوله پشتی ۰ و ۱

روش مشابهی با استفاده از برنامه‌سازی پویا برای حل مسئله کوله پشتی ۰ و ۱ با پیچیدگی زمانی شبه چندجمله‌ای وجود دارد. مانند بالا، فرض کنید {\displaystyle w_{1},\,w_{2},\,\ldots ,\,w_{n},\,W}‌ها اعداد صحیح اکیداً مثبتی هستند. {\displaystyle m[i,w]} را بیشترین ارزش قابل دستیابی، با استفاده از اشیای ۱ تا i با حد اکثر وزن w تعریف کنید.

{\displaystyle m[i,w]} را می‌توان به‌طور بازگشتی، مطابق زیر تعریف کرد:

  • {\displaystyle m[0,\,w]=0}
  • {\displaystyle m[i,\,0]=0}
  • {\displaystyle m[i,\,w]=m[i-1,\,w]} اگر {\displaystyle w_{i}>w\,\!}
  • {\displaystyle m[i,\,w]=\max(m[i-1,\,w],\,m[i-1,w-w_{i}]+v_{i})} اگر {\displaystyle w_{i}\leqslant w}.

پاسخ با محاسبهٔ {\displaystyle m[n,W]} بدست می‌آید. برای کارآمد شدن راه حل، می‌توان از جدولی برای نگهداری نتایج محاسبات قبلی استفاده کرد؛ بنابراین پیچیدگی زمانی آن {\displaystyle O(nW)} و حافظه {\displaystyle O(nW)}خواهد شد. همچنین می‌توان حجم حافظه را به {\displaystyle O(W)} کاهش داد. به این ترتیب که آرایهٔ یک بعدی{\displaystyle m[w]}، ارزش بهینه تا کنون را نشان می‌دهد. از {\displaystyle i=1} شروع کرده، آرایه را پر می‌کنیم. سپس با حرکت بر روی i، مقدار {\displaystyle m[w]} را با افزدون یک شی جدید به انتخاب‌ها، به روز آوری می‌کنیم.

الگوریتم دیگری برای مسئله کوله پشتی ۰ و ۱، در سال ۱۹۷۴ ارائه شد که گاهی «رویارویی در میانه» نیز نامیده می‌شود. این الگوریتم نسبت به تعداد اشیا نمایی است. (این اسم، از الگوریتمی مشابه در رمزنگاری نشات گرفته‌است). هنگامی که W نسبت به n بسیار بزرگتر باشد (یعنیW از 2^n هم بزرگتر باشد)، این الگوریتم نسبت به روش پویا از نظر زمانی بهینه تر است. برای مثال فرض کنیدw_i‌ها نامنفی باشند، اما صحیح نباشند. در اینجا نیز می‌توان از روش پویا استفاده کرد: اگر عددها d رقم بعد از اعشار داشته باشند، کافی است آن‌ها را در {\displaystyle 10^{d}} ضرب و سپس رند کرد (با استفاده از محاسبات ممیز ثابت). روش پویا با این تغییرات، از مرتبهٔ زمانی {\displaystyle O(nW*10^{d})} و حافظهٔ {\displaystyle O(W*10^{d})} خواهد بود.

الگوریتم «رویارویی در میانه» به صورت زیر است:

  1. مجموعهٔ {\displaystyle {1,2,\ldots ,n}} را به دو مجموعهٔ A و B با اندازهٔ نسبتاً برابر تقسیم کنید.
  2. ارزش‌ها و وزن‌های هر زیر مجموعه از هریک ازA و B را بدست آورید.
  3. برای هر زیرمجموعه از A، بهترین مکملB را از زیر مجموعه‌هایش انتخاب کنید: به عبارتی زیر مجموعه‌ای از B با بیشترین جمع ارزش کالاها، به نحوی که جمع وزن‌های دو زیر مجموعه، از {\displaystyle W} بیشتر نشود. بیشترین ارزش بدست آمده را ذخیره کنید.

این الگوریتم از مرتبهٔ حافظهٔ {\displaystyle O(2^{n/2})} است و با پیاده‌سازی بهینه گام ۳، از مرتبهٔ زمانی{\displaystyle O(n*2^{n/2})} می‌شود. (برای مثال با مرتب کردن زیرمجموعه‌های B بر حسب وزن، چشم پوشی از زیر مجموعه‌هایی از B که وزنی بیشتر از سایر زیر مجموعه‌ها با ارزش بزرگتر/مساوی دارند و استفاده از جستجوی دودویی برای یافتن بهترین تطابق). مانند روش رویارویی در میانه در رمز نگاری، استفاده از این الگوریتم با هزینه کردن حافظه (مرتبهٔ نمایی به جای مقدار ثابت) باعث بهینه شدن زمان اجرا می‌شود. می‌دانیم چنانچه بخواهیم تمام زیر مجموعه‌های {1…n} را به روش brute force بررسی کنیم، مرتبهٔ زمانی {\displaystyle O(n*2^{n})} خواهد شد اما با این الگوریتم آن را بهینه کردیم.

الگوریتم تقریبی حریصانه

George Dantzig الگوریتمی تقریبی از نوع حریصانه برای حل مسئله کوله پشتی بیکران ارائه داد.

به این ترتیب که اشیا را به ترتیب نزولی بر حسب ارزش به واحد وزن مرتب می‌کند ({\displaystyle v_{i}/w_{i}}) سپس از شی شماره ۱ شروع می‌کند. بیشترین تعداد ممکن از آن را در کوله پشتی قرار می‌دهد، تا زمانی که دیگر جای خالی ای برای آن نوع باقی نماند. آنگاه سراغ شی بعدی می‌رود. (دقت کنید که در این نسخه از سؤال، محدودیتی برای تعداد اشیا نداریم) اگر m بیشینه ارزش اشیایی باشد که در کوله پشتی جا می‌شوند، این الگوریتم حداقل به مقدار {\displaystyle m/2} دست می‌یابد. اما اگر تعداد مجاز از هر شی محدود باشد، ممکن است خروجی این الگوریتم از پاسخ بهینه بسیار دور باشد.

مسئله کوله پشتی قسمت 1
مسئله کوله پشتی قسمت 2

/توسط