خوشه بندی k میانگین (k-means Clustering) قسمت 2
معایب و مزایای خوشهبندی k-میانگین
از آنجایی که در این روش خوشهبندی، محاسبه فاصله بین نقاط توسط تابع فاصله اقلیدسی انجام میشود، از این الگوریتمها به صورت استاندارد، فقط برای مقدارهای عددی (و نه ویژگیهای کیفی) میتوان استفاده کرد. از طرف دیگر با توجه به محاسبات ساده و سریع آنها، پرکاربرد و موثر است. از طرف دیگر نسخههای تعمیم یافته از روش خوشه بندی k-میانگین نیز وجود دارد که با توابع فاصله دیگر مانند فاصله منهتن و یا فاصلههایی که برای دادههای باینری قابل استفاده است، مراحل خوشهبندی را انجام میدهد.
به منظور ارزیابی نتایج خوشهبندی از معیارهای متفاوتی کمک گرفته میشود. ممکن است از قبل برچسب خوشهها مشخص باشد و بخواهیم کارایی الگوریتم را با توجه به مقایسه برچسبهای واقعی و حاصل از خوشهبندی، اندازهگیری کنیم. در این حالت، شاخصهای ارزیابی بیرونی، بهترین راهنما و معیار برای سنجش صحت نتایج خوشهبندی محسوب میشوند. معمولا به این برچسبها، استاندارد طلایی (Golden Standard) و در کل چنین عملی را ارزیابی Benchmark میگویند. برای مثال شاخص رَند (Rand Index) یکی از این معیارها و شاخصهای بیرونی است که از محبوبیت خاصی نیز برخوردار است.
از طرف دیگر اگر هیچ اطلاعات اولیه از ساختار و دستهبندی مشاهدات وجود نداشته باشد، فقط ملاک ارزیابی، میتواند اندازههایی باشد که میزان شباهت درون خوشهها و یا عدم شباهت یا فاصله بین خوشهها را اندازه میگیرند. بنابراین برای انتخاب بهتر و موثرترین روش خوشهبندی از میزان شباهت درون خوشهها و شباهت بین خوشهها استفاده میشود. روشی که دارای میزان شباهت بین خوشهای کم و شباهت درون خوشهای زیاد باشد مناسبترین روش خواهد بود. این معیارها را به نام شاخصهای ارزیابی درونی میشناسیم. به عنوان مثال شاخص نیمرخ (silhouette) یکی از این معیارها است که شاخصی برای سنجش مناسب بودن تعلق هر مشاهده به خوشهاش ارائه میدهد. به این ترتیب معیاری برای اندازهگیری کارایی الگوریتم خوشهبندی بدست میآید.
منبع
KMeans شاید سادهترین الگوریتمِ خوشهبندی باشد که در بسیاری از مواقع جزوِ بهترین الگوریتمهای خوشهبندی نیز هست. این الگوریتم از دسته الگوریتمهایی است که بایستی تعداد خوشهها (گروه ها) را از قبل به او گفته باشیم. فرض کنید یک سری داده داریم و مانندِ درسِ شبکه های عصبی دو دسته داده داریم (پراید و اتوبوس) با این تفاوت که در یک مسئلهی خوشهبندی، نمیدانیم که کدام پراید است کدام اتوبوس؟ و فقط یک سری داده با دو ویژگی (طول ماشین و ارتفاع ماشین) در اختیار داریم. اجازه دهید اینبار این دو دسته را بدون دانستنِ برچسبِ آن ها بر روی نمودار رسم کنیم (برای اینکه بدانید چگونه این نمودار رسم می شود و بُعدهای مختلف آن چگونه ساخته میشود، درسِ شبکهی عصبی را خوانده باشید) به صورت ساده، ما یک تعداد ماشین (اتومبیل) داریم که هر کدام ارتفاع و طولِ مشخصی را دارند. آنها را به این گونه در دو بُعد در شکلِ زیر نمایش میدهیم):
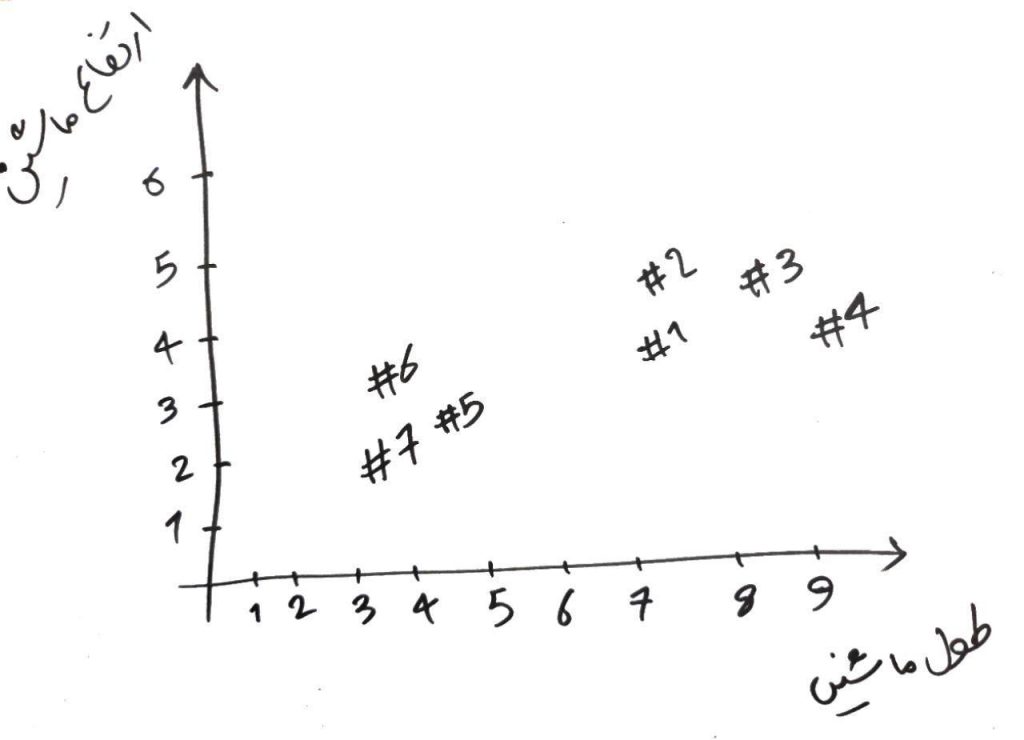
برای مثال، ماشین شمارهی ۴#، دارای طولِ ۹ و ارتفاع ۴ است. در الگوریتمِ KMeans بایستی تعدادی نقطه در فضا ایجاد کنیم. تعداد این نقاط باید به تعداد خوشههایی که میخواهیم در نهایت به آن برسیم، باشد (مثلا فرض کنید میخواهیم دادهها را به ۲خوشه تقسیمبندی کنیم، پس ۲نقطه به صورت تصادفی در فضای ۲بُعدیِ شکلِ بالا رسم میکنیم). شکل زیر را نگاه کنید:
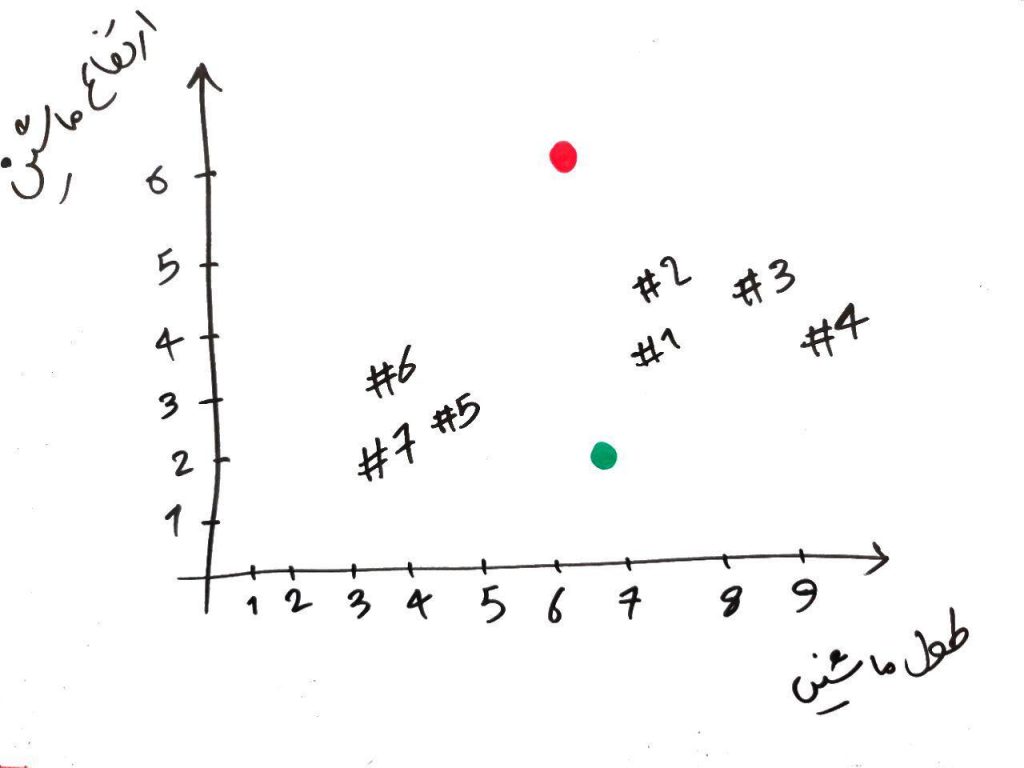
الان ما دو نقطهی سبز و قرمز انتخاب کردیم و این دو نقطه را جایی در فضا (به صورت تصادفی) قرار دادیم. حال فاصلهی هر کدام از نمونهها را (۷ماشین) با این دو نقطه حساب میکنیم. برای این کار میتوانیم از فاصله منهتن (Manhatan) استفاده کنیم. در واقع برای هر کدام از نمونهها نسبت به دو نقطهی سبز و قرمز در هر بُعد، با هم مقایسه کرده و از هم کم (تفاضل) میکنیم، سپس نتیجهی کم کردنِ هر کدام از بُعد ها را با یکدیگر جمع میکنیم.
بعد از محاسبهی فاصلهی هر کدام از نمونهها با دو نقطهی سبز و قرمز، برای هر نمونه، اگر آن نمونه به نقطهی سبز نزدیکتر بود، آن نمونه سبز میشود (یعنی به خوشهی سبزها می رود) و اگر به قرمز نزدیکتر بود به خوشهی قرمزها می رود. مانند شکل زیر برای مثال بالا:
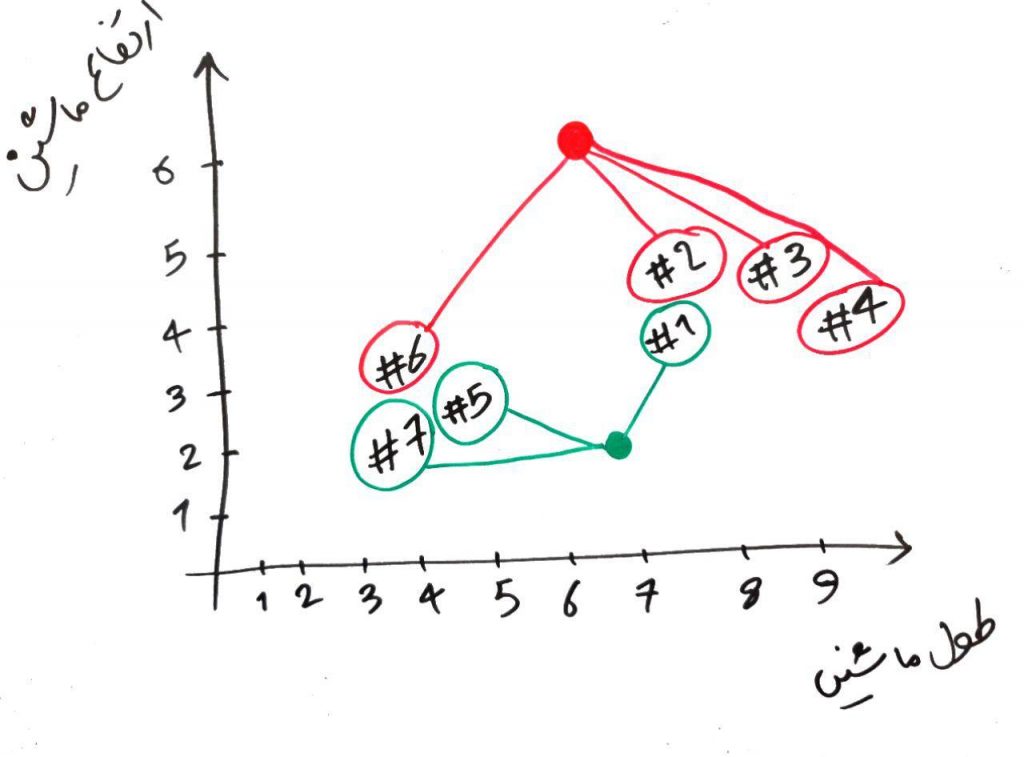
الان یک مرحله از الگوریتم را تمام کرده ایم. یعنی یک دور از الگوریتم تمام شد و میتوانیم همین جا هم الگوریتم را تمام کنیم و نقاطی که سبز رنگ شده اند را در خوشهی سبزها و نقاطی که قرمز رنگ شدهاند را در خوشهی قرمزها قرار دهیم. ولی الگوریتمِ KMeans را بایستی چندین مرتبه تکرار کرد. ما هم همین کار را انجام میدهیم. برای شروعِ مرحلهی بعد، باید نقطهی سبز و قرمز را جابهجا کنیم و به جایی ببریم که میانگینِ نمونههای مختلف در خوشهی مربوط به خودشان قرار دارد. یعنی مثلا برای نقطه قرمز بایستی نقطه را به جایی ببریم که میانگینِ نمونههای قرمزِ دیگر (در مرحلهی قبلی) باشد. برای نقطه سبز هم همین طور. این کار را در شکل زیر انجام دادهایم:
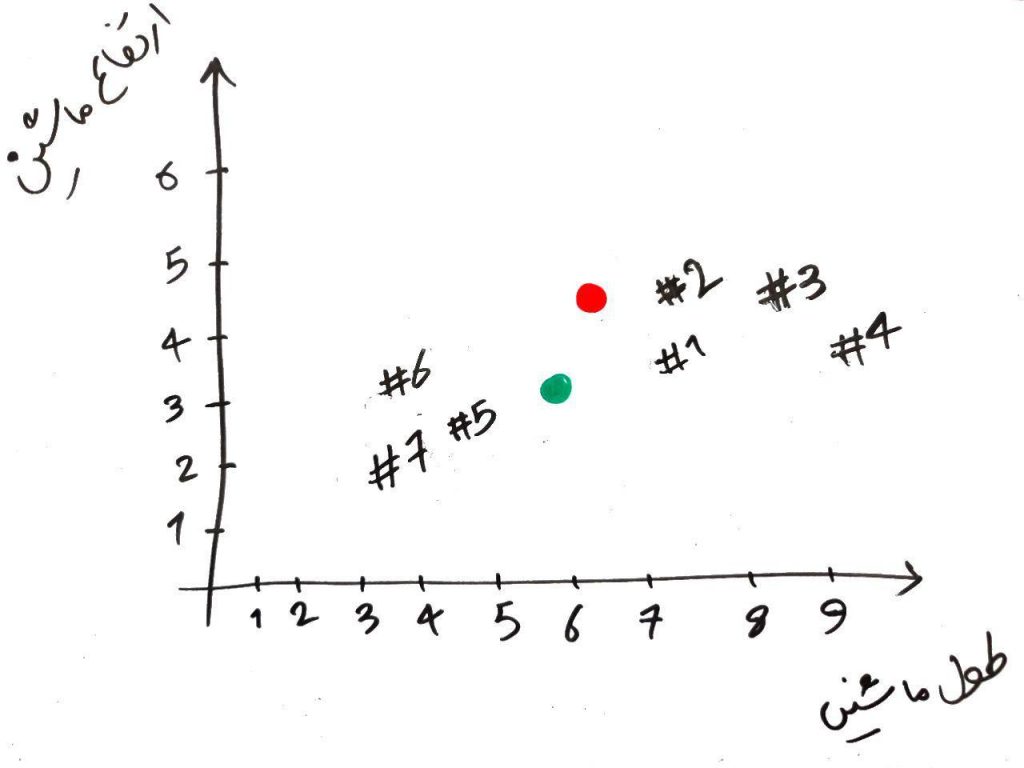
الان دو نقطه قرمز و سبز جابهجا شدند. حال بایستی دوباره تمامیِ نمونهها را هر کدام با دو نقطهی سبز و قرمز مقایسه کنیم و مانند دور قبلی، آن نمونههایی که به نقطهی قرمز نزدیکتر هستند، خوشهی قرمز و آن هایی که به نقطهی سبز نزدیک هستند رنگِ سبز میگیرند. مانند شکل زیر:
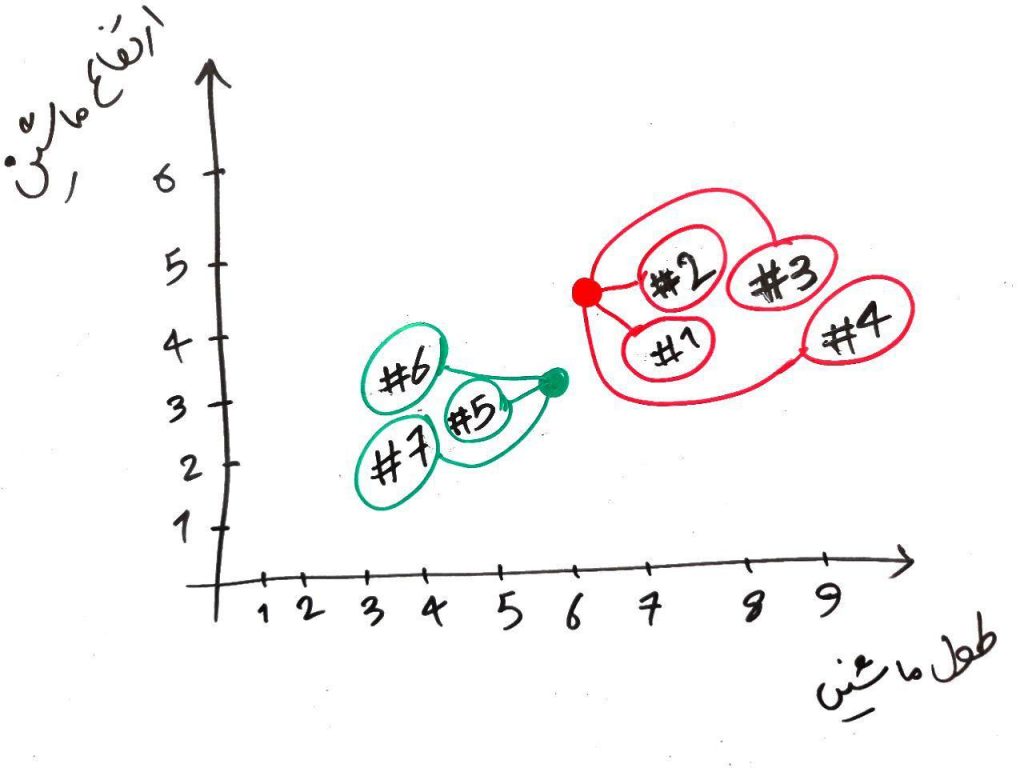
دورِ دوم نیز به اتمام رسید و به نظرْ الگوریتم خوشههای خوبی را تشخیص داد. ولی اجازه بدهید یک دور دیگر نیز الگوریتم را ادامه دهیم. مانند شکل زیر دور سوم را انجام می شود (یعنی نقاطِ قرمز و سبز به مرکز خوشهی خود (در مرحلهی قبلی) میروند و فاصلهی هر کدام از نمونهها دوباره با نقاطِ قرمز و سبز (در محلِ جدید) محاسبه شده و هر کدام همرنگِ نزدیکترین نقطهی قرمز یا سبز میشود):
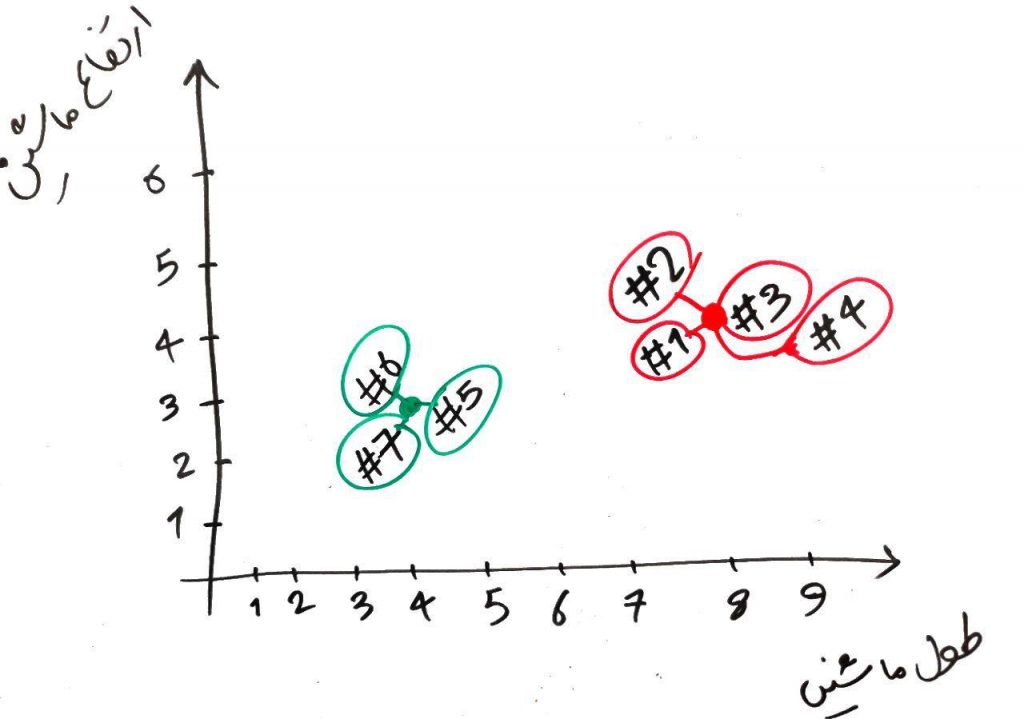
همان طور که میبینید در انتهای دورِ سوم، تغییری در خوشهی هر کدام از نمونهها رخ نداد. یعنی سبزها سبز ماندند و قرمزها، قرمز.این یکی از شروطی است که میتواند الگوریتم را خاتمه دهد. یعنی الگوریتمْ وقتی به این حالت رسید که در چند دورِ متوالی تغییری در خوشهی نمونهها (در اینجا ماشینها) به وجود نیامد، یعنی الگوریتمْ دیگر نمیتواند زیاد تغییر کند و این حالتِ پایانی برای خوشههاست. البته میتوان شرطی دیگر نیز برای پایان الگوریتم در نظر گرفت. برای مثال الگوریتمْ حداکثر در ۲۰دورِ متوالی میتواند عملیات را انجام دهد و دورِ ۲۰ام آخرین دورِ الگوریتم خواهد بود و الگوریتم دیگر بیشتر از آن پیشروی نخواهد کرد. به طور کل در الگوریتمهای مبتنی بر دور (Iterative Algorithms) میتوان تعدادِ دورها را محدود کرد تا الگوریتمْ بینهایت دور نداشته باشد.
همان طور که دیدیم، این الگوریتم میتواند یک گروهبندیِ ذاتی برای دادهها بسازد، بدون اینکه برچسب دادهها یا نوع آنها را بداند.
کاربردهای خوشهبندی بسیار زیاد است. برای مثال فرض کنید میخواهید مشتریانِ خود را (که هر کدام دارای ویژگیهای مختلفی هستند) به خوشههای متفاوتی تقسیم کنید و هر کدام از خوشهها را به صورتِ جزئی مورد بررسی قرار دهید. ممکن است با مطالعهی خوشههایی از مشتریان به این نتیجه برسید که برخی از آنها که تعدادشان هم زیاد است، علارغم خرید با توالیِ زیاد، در هر بار خرید پول کمتری خرج میکنند. با این تحلیلهایی که از خوشهبندی به دست میآید یک مدیرِ کسب و کار میتواند به تحلیلدادهها و سپس تصمیمگیریِ درستتری برسد.
منبع
مروری بر الگوریتم K-Means
برای مشخص کردن شباهت دادهها از معیار و راههای مختلفی استفاده میشه که یکی از اونا فاصله اقلیدسی هست و در اینجا هم ما از اون استفاده میکنیم.
اساس کار این الگوریتم به این صورت هست که اول باید تعداد خوشههایی که مد نظر داریم رو مشخص کنیم. بعد از اون الگوریتم از مجموعه داده موجود، به تعداد خوشههایی که مشخص کردیم میاد و به صورت تصادفی تعدادی رو به عنوان مرکز هر خوشه انتخاب میکنه. در مراحل بعدی به این خوشهها دادههای دیگری رو اضافه میکنه و میانگین دادههای هر خوشه رو به عنوان مرکز اون خوشه در نظر میگیره. بعد از انتخاب مراکز خوشه جدید، دادههای موجود در خوشهها دوباره مشخص میشن. دلیلش هم این هست که در هر خوشه با انتخاب مرکز خوشه جدید ممکنه که بعضی از دادههای اون خوشه از اون به بعد به خوشه(های) دیگهای تعلق پیدا کنن.
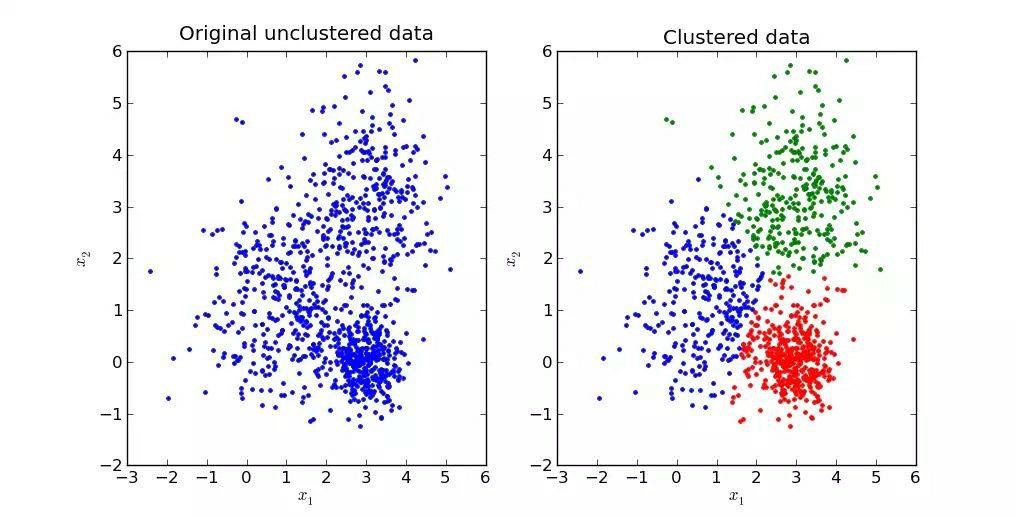
در شکل زیر نمونهای از خوشهبندی نشون داده شده که در اون دادهها به سه خوشه تقسیم و به کمک سه رنگ نمایش داده شدن.
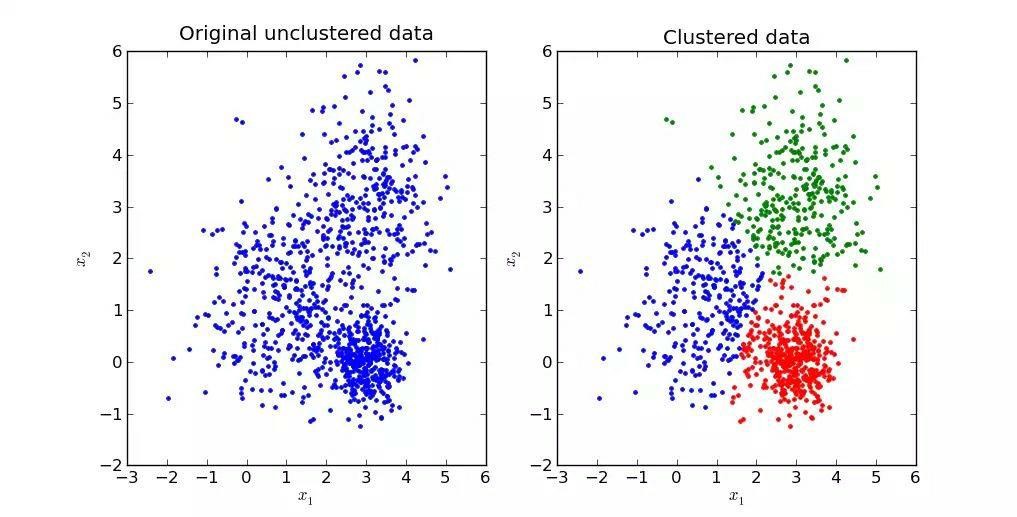
برای درک بهتر نحوه کار الگوریتم K-Means از مثال زیر استفاده میکنم:
فرض میکنیم که مجموعه دادهای داریم که شامل هر ۷ رکورد هست و همه رکوردهای اون ۲ ویژگی یا خصوصیت A و B رو دارن. (دز اینجا میتونیم این ویژگیها رو به عنوان طول و عرض در یک صفحه دو بعدی در نظر بگیریم)
| رکورد | A | B |
|---|---|---|
| ۱ | ۱.۰ | ۱.۰ |
| ۲ | ۱.۵ | ۲.۰ |
| ۳ | ۳.۰ | ۴.۰ |
| ۴ | ۵.۰ | ۷.۰ |
| ۵ | ۳.۵ | ۵.۰ |
| ۶ | ۴.۵ | ۵.۰ |
| ۷ | ۳.۵ | ۴.۵ |
فرض میکنیم که قراره دادهها به ۲ خوشه تقسیم بشن. پس برای این منظور به صورت تصادفی ۲ رکورد رو به عنوان مرکز این ۲ خوشه در نظر میگیریم.
| رکورد | مختصات | |
|---|---|---|
| خوشه ۱ | ۱ | (۱.۰ و ۱.۰) |
| خوشه ۲ | ۴ | (۷.۰ و ۵.۰) |
در ادامه الگوریتم دادهها رو به خوشهای که فاصله اقلیدسی کمتری تا مرکز اون داره اختصاص میده. و هربار که داده جدیدی رو به یک خوشه اضافه میکنه مرکز اون خوشه رو هم دوباره محاسبه و مشخص میکنه.
| خوشه ۱ | خوشه ۲ | |||
|---|---|---|---|---|
| گام | رکورد | مرکز خوشه | رکورد | مرکز خوشه |
| ۱ | ۱ | (۱.۰ و ۱.۰) | ۴ | (۷.۰ و ۵.۰) |
| ۲ | ۱ و ۲ | (۱.۵ و ۱.۲) | ۴ | (۷.۰ و ۵.۰) |
| ۳ | ۱ و ۲ و ۳ | (۲.۳ و ۱.۸) | ۴ | (۷.۰ و ۵.۰) |
| ۴ | ۱ و ۲ و ۳ | (۲.۳ و ۱.۸) | ۴ و ۵ | (۶.۰ و ۴.۲) |
| ۵ | ۱ و ۲ و ۳ | (۲.۳ و ۱.۸) | ۴ و ۵ و ۶ | (۵.۷ و ۴.۳) |
| ۶ | ۱ و ۲ و ۳ | (۲.۳ و ۱.۸) | ۴ و ۵ و ۶ و ۷ | (۵.۴ و ۴.۱) |
پس در ادامه مرکزهای خوشهها به صورت زیر در میان.
| رکورد | مرکز خوشه | |
|---|---|---|
| خوشه ۱ | ۱ و ۲ و ۳ | (۲.۳ و ۱.۸) |
| خوشه ۲ | ۴ و ۵ و ۶ و ۷ | (۵.۴ و ۴.۱) |
در ادامه فاصله دادهها تا این مرکزهای خوشههای جدید به شکل جدول زیر در میان.
| رکورد | فاصله تا خوشه ۱ | فاصله تا خوشه ۲ |
|---|---|---|
| ۱ | ۱.۵ | ۵.۴ |
| ۲ | ۰.۴ | ۴.۳ |
| ۳ | ۲.۱ | ۱.۸ |
| ۴ | ۵.۷ | ۱.۸ |
| ۵ | ۳.۲ | ۰.۷ |
| ۶ | ۳.۸ | ۰.۶ |
| ۷ | ۲.۸ | ۱.۱ |
در نتیجه و بر اساس این مراحل و اطلاعات مشاهده میکنیم رکورد ۳ که مربوط به خوشه ۱ بوده، فاصلش تا مرکز خوشه ۲ کمتر میشه. پس این رکورد رو باید به خوشه ۲ اختصاص بدیم.
| رکورد | مرکز خوشه | |
|---|---|---|
| خوشه ۱ | ۱ و ۲ | خوشه ۱ |
| خوشه ۲ | ۳ و ۴ و ۵ و ۶ و ۷ | خوشه ۲ |
و کل این فرایند و مراحل تا زمانی انجام میشه که تغییر و جابجایی در خوشهها اتفاق نیفته.
این الگوریتم رو به راحتی و به کمک زبانهای برنامهنویسی مختلفی میشه پیادهسازی کرد و در ادامه من پیادهسازی این الگوریتم رو برای همین مثال و به زبان جاوا و پایتون در اینجا شرح میدم.
پیادهسازی الگوریتم K-Means به زبان Java
import java.util.ArrayList;
public class KMeans_Ex {
private static final int NUM_CLUSTERS = 2; // Total clusters.
private static final int TOTAL_DATA = 7; // Total data points.
private static final double SAMPLES[][] = new double[][]{{1.0, 1.0},
{1.5, 2.0},
{3.0, 4.0},
{5.0, 7.0},
{3.5, 5.0},
{4.5, 5.0},
{3.5, 4.5}};
private static ArrayList < Data > dataSet = new ArrayList < Data > ();
private static ArrayList < Centroid > centroids = new ArrayList < Centroid > ();
private static void initialize() {
System.out.println("Centroids initialized at:");
centroids.add(new Centroid(1.0, 1.0)); // lowest set.
centroids.add(new Centroid(5.0, 7.0)); // highest set.
System.out.println(" (" + centroids.get(0).X() + ", " + centroids.get(0).Y() + ")");
System.out.println(" (" + centroids.get(1).X() + ", " + centroids.get(1).Y() + ")");
System.out.print("\n");
return;
}
private static void kMeanCluster() {
final double bigNumber = Math.pow(10, 10); // some big number that's sure to be larger than our data range.
double minimum = bigNumber; // The minimum value to beat.
double distance = 0.0; // The current minimum value.
int sampleNumber = 0;
int cluster = 0;
boolean isStillMoving = true;
Data newData = null;
// Add in new data, one at a time, recalculating centroids with each new one.
while (dataSet.size() < TOTAL_DATA) {
newData = new Data(SAMPLES[sampleNumber][0], SAMPLES[sampleNumber][1]);
dataSet.add(newData);
minimum = bigNumber;
for (int i = 0; i < NUM_CLUSTERS; i++) {
distance = dist(newData, centroids.get(i));
if (distance < minimum) {
minimum = distance;
cluster = i;
}
}
newData.cluster(cluster);
// calculate new centroids.
for (int i = 0; i < NUM_CLUSTERS; i++) {
int totalX = 0;
int totalY = 0;
int totalInCluster = 0;
for (int j = 0; j < dataSet.size(); j++) { if (dataSet.get(j).cluster() == i) { totalX += dataSet.get(j).X(); totalY += dataSet.get(j).Y(); totalInCluster++; } } if (totalInCluster > 0) {
centroids.get(i).X(totalX / totalInCluster);
centroids.get(i).Y(totalY / totalInCluster);
}
}
sampleNumber++;
}
// Now, keep shifting centroids until equilibrium occurs.
while (isStillMoving) {
// calculate new centroids.
for (int i = 0; i < NUM_CLUSTERS; i++) {
int totalX = 0;
int totalY = 0;
int totalInCluster = 0;
for (int j = 0; j < dataSet.size(); j++) { if (dataSet.get(j).cluster() == i) { totalX += dataSet.get(j).X(); totalY += dataSet.get(j).Y(); totalInCluster++; } } if (totalInCluster > 0) {
centroids.get(i).X(totalX / totalInCluster);
centroids.get(i).Y(totalY / totalInCluster);
}
}
// Assign all data to the new centroids
isStillMoving = false;
for (int i = 0; i < dataSet.size(); i++) {
Data tempData = dataSet.get(i);
minimum = bigNumber;
for (int j = 0; j < NUM_CLUSTERS; j++) {
distance = dist(tempData, centroids.get(j));
if (distance < minimum) {
minimum = distance;
cluster = j;
}
}
tempData.cluster(cluster);
if (tempData.cluster() != cluster) {
tempData.cluster(cluster);
isStillMoving = true;
}
}
}
return;
}
/**
* // Calculate Euclidean distance.
*
* @param d - Data object.
* @param c - Centroid object.
* @return - double value.
*/
private static double dist(Data d, Centroid c) {
return Math.sqrt(Math.pow((c.Y() - d.Y()), 2) + Math.pow((c.X() - d.X()), 2));
}
private static class Data {
private double mX = 0;
private double mY = 0;
private int mCluster = 0;
public Data() {
return;
}
public Data(double x, double y) {
this.X(x);
this.Y(y);
return;
}
public void X(double x) {
this.mX = x;
return;
}
public double X() {
return this.mX;
}
public void Y(double y) {
this.mY = y;
return;
}
public double Y() {
return this.mY;
}
public void cluster(int clusterNumber) {
this.mCluster = clusterNumber;
return;
}
public int cluster() {
return this.mCluster;
}
}
private static class Centroid {
private double mX = 0.0;
private double mY = 0.0;
public Centroid() {
return;
}
public Centroid(double newX, double newY) {
this.mX = newX;
this.mY = newY;
return;
}
public void X(double newX) {
this.mX = newX;
return;
}
public double X() {
return this.mX;
}
public void Y(double newY) {
this.mY = newY;
return;
}
public double Y() {
return this.mY;
}
}
public static void main(String[] args) {
initialize();
kMeanCluster();
// Print out clustering results.
for (int i = 0; i < NUM_CLUSTERS; i++) {
System.out.println("Cluster " + i + " includes:");
for (int j = 0; j < TOTAL_DATA; j++) {
if (dataSet.get(j).cluster() == i) {
System.out.println(" (" + dataSet.get(j).X() + ", " + dataSet.get(j).Y() + ")");
}
} // j
System.out.println();
} // i
// Print out centroid results.
System.out.println("Centroids finalized at:");
for (int i = 0; i < NUM_CLUSTERS; i++) {
System.out.println(" (" + centroids.get(i).X() + ", " + centroids.get(i).Y() + ")");
}
System.out.print("\n");
return;
}
پیادهسازی الگوریتم K-Means به زبانPython
import math
NUM_CLUSTERS = 2
TOTAL_DATA = 7
LOWEST_SAMPLE_POINT = 0 # element 0 of SAMPLES.
HIGHEST_SAMPLE_POINT = 3 # element 3 of SAMPLES.
BIG_NUMBER = math.pow(10, 10)
SAMPLES = [[1.0, 1.0], [1.5, 2.0], [3.0, 4.0], [5.0, 7.0], [3.5, 5.0], [4.5, 5.0], [3.5, 4.5]]
data = []
centroids = []
class DataPoint:
def __init__(self, x, y):
self.x = x
self.y = y
def set_x(self, x):
self.x = x
def get_x(self):
return self.x
def set_y(self, y):
self.y = y
def get_y(self):
return self.y
def set_cluster(self, clusterNumber):
self.clusterNumber = clusterNumber
def get_cluster(self):
return self.clusterNumber
class Centroid:
def __init__(self, x, y):
self.x = x
self.y = y
def set_x(self, x):
self.x = x
def get_x(self):
return self.x
def set_y(self, y):
self.y = y
def get_y(self):
return self.y
def initialize_centroids():
# Set the centoid coordinates to match the data points furthest from each other.
# In this example, (1.0, 1.0) and (5.0, 7.0)
centroids.append(Centroid(SAMPLES[LOWEST_SAMPLE_POINT][0], SAMPLES[LOWEST_SAMPLE_POINT][1]))
centroids.append(Centroid(SAMPLES[HIGHEST_SAMPLE_POINT][0], SAMPLES[HIGHEST_SAMPLE_POINT][1]))
print("Centroids initialized at:")
print("(", centroids[0].get_x(), ", ", centroids[0].get_y(), ")")
print("(", centroids[1].get_x(), ", ", centroids[1].get_y(), ")")
print()
return
def initialize_datapoints():
# DataPoint objects' x and y values are taken from the SAMPLE array.
# The DataPoints associated with LOWEST_SAMPLE_POINT and HIGHEST_SAMPLE_POINT are initially
# assigned to the clusters matching the LOWEST_SAMPLE_POINT and HIGHEST_SAMPLE_POINT centroids.
for i in range(TOTAL_DATA):
newPoint = DataPoint(SAMPLES[i][0], SAMPLES[i][1])
if (i == LOWEST_SAMPLE_POINT):
newPoint.set_cluster(0)
elif (i == HIGHEST_SAMPLE_POINT):
newPoint.set_cluster(1)
else:
newPoint.set_cluster(None)
data.append(newPoint)
return
def get_distance(dataPointX, dataPointY, centroidX, centroidY):
# Calculate Euclidean distance.
return math.sqrt(math.pow((centroidY - dataPointY), 2) + math.pow((centroidX - dataPointX), 2))
def recalculate_centroids():
totalX = 0
totalY = 0
totalInCluster = 0
for j in range(NUM_CLUSTERS):
for k in range(len(data)):
if (data[k].get_cluster() == j):
totalX += data[k].get_x()
totalY += data[k].get_y()
totalInCluster += 1
if (totalInCluster > 0):
centroids[j].set_x(totalX / totalInCluster)
centroids[j].set_y(totalY / totalInCluster)
return
def update_clusters():
isStillMoving = 0
for i in range(TOTAL_DATA):
bestMinimum = BIG_NUMBER
currentCluster = 0
for j in range(NUM_CLUSTERS):
distance = get_distance(data[i].get_x(), data[i].get_y(), centroids[j].get_x(), centroids[j].get_y())
if (distance < bestMinimum):
bestMinimum = distance
currentCluster = j
data[i].set_cluster(currentCluster)
if (data[i].get_cluster() is None or data[i].get_cluster() != currentCluster):
data[i].set_cluster(currentCluster)
isStillMoving = 1
return isStillMoving
def perform_kmeans():
isStillMoving = 1
initialize_centroids()
initialize_datapoints()
while (isStillMoving):
recalculate_centroids()
isStillMoving = update_clusters()
return
def print_results():
for i in range(NUM_CLUSTERS):
print("Cluster ", i, " includes:")
for j in range(TOTAL_DATA):
if (data[j].get_cluster() == i):
print("(", data[j].get_x(), ", ", data[j].get_y(), ")")
print()
return
perform_kmeans()
print_results()
در این الگوریتم وقتی مرکز خوشه محاسبه میشه خیلی پیش میاد که این مرکز خوشه محاسبهشده در بین دادههای واقعی موجود نباشه و صرفا یه میانگین محسوب میشه که همین موضوع باعث مقاوم نبودن این الگوریتم در برابر دادههای پرت مبشه. برای حل این مشکل الگوریتمی پیشنهاد شده به نام K-Medoids که در این الگوریتم مرکز خوشه جدید وقتی محاسبه میشه خودش هم در بین دادههای اصلی موجود هست. با کمی تغییر در الگوریتم K-Means میتونیم K-Medoids رو هم داشته باشیم.
این برنامه در سایت گیتلب قابل دسترس هست و شما میتونید اون رو تغییر بدین و بهترش کنید.
پیادهسازی الگوریتم KMEANS به زبان JAVA در گیتلب
پیادهسازی الگوریتم KMEANS به زبان PYTHON در گیتلب