کد الگوریتم Canny در #C
الگوریتم Canny
لبه یاب کنی توسط جان اف کنی در سال 1986 ایجاد شد و هنوز یک لبه یاب استاندارد و با دقت و کیفیت بالا میباشد.الگوریتم لبه یابی کنی یکی از بهترین لبه یابها تا به امروز است. در ادامه روش کار این الگوریتم و هم چنین کد الگوریتم Canny در #C را بررسی خواهیم کرد. این الگوریتم لبه یابی از سه بخش اصلی زیر تشکیل شده:
- تضعیف نویز
- پیدا کردن نقاطی که بتوان آنها را به عنوان لبه در نظر گرفت
- حذب نقاطی که احتمال لبه بودن آنها کم است
معیارهایی که در لبه یاب کنی مطرح است:
1 -پایین آوردن نرخ خطا- یعنی تا حد امکان هیچ لبه ای در تصویر نباید گم شود و هم چنین هیچ چیزی که لبه نیست نباید به جای لبه فرض شود. لبه هان پیدا شده تا حد ممکن به لبه ها اصلی
نزدیک باشند.
2 -لبه در مکان واقعی خود باشد- یعنی تا حد ممکن لبه ها کمترین فاصله را با مکان واقعی خود داشته باشند.
3 -بران هر لبه فقط یک پاسخ داشته باشیم.
4 -لبه ها کمترین ضخامت را داشته باشند- (در صورت امکان یک پیکسل).
لبه یاب کنی بخاطر توانایی در تولید لبه های نازک تا حد یک ییکسل برای لبه های پیوسته معروف شده است. این لبه یاب شامل چهار مرحله و چهار ورودی زیر است:
یک تصویر ورودی
یک پارامتر به نام سیگما جهت مقدار نرم کنندگی تصویر
یک حد آستانه بالا (Th)
یک حد آستانه پایین (Tl)
مراحل الگوریتم Canny:
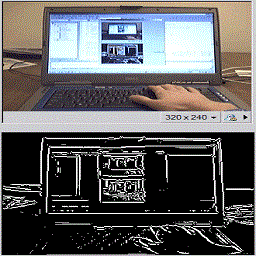
1- در ابتدا باید تصویر رنگی را به جهت لبه یابی بهتر به یک تصویر سطح خاکسترن تبدیب کرد.
2- نویز را از تصویر دریافتی حذف کرد. بدلیل اینکه فیلتر گاوسین از یک ماسک ساده برای حذف نویز استفاده می کند لبه یاب کنی در مرحله اول برای حذف نویز آن را بکار میگیرد.
3- در یک تصویر سطح خاکستر جایی را که بیشترین تغییرات را داشته باشند به عنوان لبه در نظر گرفته می شوند و این مکانها با گرفتن گرادیان تصویر با استفاده عملگر سوبل بدست می آیند. سپس لبه های مات یافت شده به لبه های تیزتر تبدیل می شوند.
4- برخی از لبه های کشف شده واقعا لبه نیستند و در واقع نویز هستند که باید آنها توسط حد آستانه هیسترزیس فیلتر شوند.هیسترزیس از دو حد آستانه بالاتر (Th) و حد آستانه پایین تر (Tl) استفاده کرده و کنی پیشنهاد می کند که نسبت استانه بالا به پایین سه به یک باشد.
این روش بیشتر به کشف لبه های ضعیف به درستی می پردازد و کمتر فریب نویز را می خورد و از بقیه روش ها بهتر است.


کد الگوریتم Canny در #C:
الگوریتم در 5 مرحله جداگانه اجرا می شود:
1. صاف کردن: تار شدن تصویر برای حذف نویز. پیکربندی توسط فیلتر گاوسی با اندازه مشخص هسته (N) و پارامتر پوشش گاوسی سیگما. پوشاننده فیلتر گاوسی توسط تابع زیر تولید می شود:
private void GenerateGaussianKernel(int N, float S ,out int Weight)
{
float Sigma = S ;
float pi;
pi = (float)Math.PI;
int i, j;
int SizeofKernel=N;
float [,] Kernel = new float [N,N];
GaussianKernel = new int [N,N];
float[,] OP = new float[N, N];
float D1,D2;
D1= 1/(2*pi*Sigma*Sigma);
D2= 2*Sigma*Sigma;
float min=1000;
for (i = -SizeofKernel / 2; i <= SizeofKernel / 2; i++)
{
for (j = -SizeofKernel / 2; j <= SizeofKernel / 2; j++)
{
Kernel[SizeofKernel / 2 + i, SizeofKernel / 2 + j] = ((1 / D1) * (float)Math.Exp(-(i * i + j * j) / D2));
if (Kernel[SizeofKernel / 2 + i, SizeofKernel / 2 + j] < min)
min = Kernel[SizeofKernel / 2 + i, SizeofKernel / 2 + j];
}
}
int mult = (int)(1 / min);
int sum = 0;
if ((min > 0) && (min < 1))
{
for (i = -SizeofKernel / 2; i <= SizeofKernel / 2; i++)
{
for (j = -SizeofKernel / 2; j <= SizeofKernel / 2; j++)
{
Kernel[SizeofKernel / 2 + i, SizeofKernel / 2 + j] = (float)Math.Round(Kernel[SizeofKernel / 2 + i, SizeofKernel / 2 + j] * mult, 0);
GaussianKernel[SizeofKernel / 2 + i, SizeofKernel / 2 + j] = (int)Kernel[SizeofKernel / 2 + i, SizeofKernel / 2 + j];
sum = sum + GaussianKernel[SizeofKernel / 2 + i, SizeofKernel / 2 + j];
}
}
}
else
{
sum = 0;
for (i = -SizeofKernel / 2; i <= SizeofKernel / 2; i++)
{
for (j = -SizeofKernel / 2; j <= SizeofKernel / 2; j++)
{
Kernel[SizeofKernel / 2 + i, SizeofKernel / 2 + j] = (float)Math.Round(Kernel[SizeofKernel / 2 + i, SizeofKernel / 2 + j] , 0);
GaussianKernel[SizeofKernel / 2 + i, SizeofKernel / 2 + j] = (int)Kernel[SizeofKernel / 2 + i, SizeofKernel / 2 + j];
sum = sum + GaussianKernel[SizeofKernel / 2 + i, SizeofKernel / 2 + j];
}
}
}
//Normalizing kernel Weight
Weight= sum;
return;
}
زیر روال ذیل نویز را توسط فیلتر گوسی حذف می کند.
private int[,] GaussianFilter(int[,] Data)
{
GenerateGaussianKernel(KernelSize, Sigma,out KernelWeight);
int[,] Output = new int[Width, Height];
int i, j,k,l;
int Limit = KernelSize /2;
float Sum=0;
Output = Data; // Removes Unwanted Data Omission due to kernel bias while convolution
for (i = Limit; i <= ((Width - 1) - Limit); i++)
{
for (j = Limit; j <= ((Height - 1) - Limit); j++)
{
Sum = 0;
for (k = -Limit; k <= Limit; k++)
{
for (l = -Limit; l <= Limit; l++)
{
Sum = Sum + ((float)Data[i + k, j + l] * GaussianKernel [Limit + k, Limit + l]);
}
}
Output[i, j] = (int)(Math.Round(Sum/ (float)KernelWeight));
}
}
return Output;
}
2. پیدا کردن شیب ها: لبه ها باید مشخص شوند، جایی که شیب های تصویر بزرگ می شوند.
ماسک های سوبل X و Y برای تولید گرادیان های تصویر X و Y استفاده می شود؛ تابع بعدی تمایز را با استفاده از فیلتر ماسک sobel اعمال می کند.
private float[,] Differentiate(int[,] Data, int[,] Filter)
{
int i, j,k,l, Fh, Fw;
Fw = Filter.GetLength(0);
Fh = Filter.GetLength(1);
float sum = 0;
float[,] Output = new float[Width, Height];
for (i = Fw / 2; i <= (Width - Fw / 2) - 1; i++)
{
for (j = Fh / 2; j <= (Height - Fh / 2) - 1; j++)
{
sum=0;
for(k=-Fw/2; k<=Fw/2; k++)
{
for(l=-Fh/2; l<=Fh/2; l++)
{
sum=sum + Data[i+k,j+l]*Filter[Fw/2+k,Fh/2+l];
}
}
Output[i,j]=sum;
}
}
return Output;
}
3. توقیف غیر حداکثر: فقط حداکثرهای محلی باید به عنوان لبه ها مشخص شود.
ما جهت گرادیان را پیدا می کنیم و با استفاده از این جهت، ما توقیف غیر حداکثر را انجام می دهیم (“پردازش تصویر دیجیتال- آموزش توسط گنزالس-پیرسون ” را بخوانید)
// Perform Non maximum suppression:
// NonMax = Gradient;
for (i = 0; i <= (Width - 1); i++)
{
for (j = 0; j <= (Height - 1); j++)
{
NonMax[i, j] = Gradient[i, j];
}
}
int Limit = KernelSize / 2;
int r, c;
float Tangent;
for (i = Limit; i <= (Width - Limit) - 1; i++)
{
for (j = Limit; j <= (Height - Limit) - 1; j++)
{
if (DerivativeX[i, j] == 0)
Tangent = 90F;
else
Tangent = (float)(Math.Atan(DerivativeY[i, j] / DerivativeX[i, j]) * 180 / Math.PI); //rad to degree
//Horizontal Edge
if (((-22.5 < Tangent) && (Tangent <= 22.5)) || ((157.5 < Tangent) && (Tangent <= -157.5)))
{
if ((Gradient[i, j] < Gradient[i, j + 1]) || (Gradient[i, j] < Gradient[i, j - 1]))
NonMax[i, j] = 0;
}
//Vertical Edge
if (((-112.5 < Tangent) && (Tangent <= -67.5)) || ((67.5 < Tangent) && (Tangent <= 112.5)))
{
if ((Gradient[i, j] < Gradient[i + 1, j]) || (Gradient[i, j] < Gradient[i - 1, j]))
NonMax[i, j] = 0;
}
//+45 Degree Edge
if (((-67.5 < Tangent) && (Tangent <= -22.5)) || ((112.5 < Tangent) && (Tangent <= 157.5)))
{
if ((Gradient[i, j] < Gradient[i + 1, j - 1]) || (Gradient[i, j] < Gradient[i - 1, j + 1]))
NonMax[i, j] = 0;
}
//-45 Degree Edge
if (((-157.5 < Tangent) && (Tangent <= -112.5)) || ((67.5 < Tangent) && (Tangent <= 22.5)))
{
if ((Gradient[i, j] < Gradient[i + 1, j + 1]) || (Gradient[i, j] < Gradient[i - 1, j - 1]))
NonMax[i, j] = 0;
}
}
}
4. آستانه دوگانه: لبه های بالقوه توسط آستانه تعیین می شود.
5. ردیابی لبه توسط هیسترسیس: لبه های نهایی توسط توقیف تمام لبه هایی که به یک لبه بسیار قطعی (قوی) متصل نیستند، مشخص می شوند.
private void HysterisisThresholding(int[,] Edges)
{
int i, j;
int Limit= KernelSize/2;
for (i = Limit; i <= (Width - 1) - Limit; i++)
for (j = Limit; j <= (Height - 1) - Limit; j++)
{
if (Edges[i, j] == 1)
{
EdgeMap[i, j] = 1;
}
}
for (i = Limit; i <= (Width - 1) - Limit; i++)
{
for (j = Limit; j <= (Height - 1) - Limit; j++)
{
if (Edges[i, j] == 1)
{
EdgeMap[i, j] = 1;
Travers(i, j);
VisitedMap[i, j] = 1;
}
}
}
return;
}
//Recursive Procedure
private void Travers(int X, int Y)
{
if (VisitedMap[X, Y] == 1)
{
return;
}
//1
if (EdgePoints[X + 1, Y] == 2)
{
EdgeMap[X + 1, Y] = 1;
VisitedMap[X + 1, Y] = 1;
Travers(X + 1, Y);
return;
}
//2
if (EdgePoints[X + 1, Y - 1] == 2)
{
EdgeMap[X + 1, Y - 1] = 1;
VisitedMap[X + 1, Y - 1] = 1;
Travers(X + 1, Y - 1);
return;
}
//3
if (EdgePoints[X, Y - 1] == 2)
{
EdgeMap[X , Y - 1] = 1;
VisitedMap[X , Y - 1] = 1;
Travers(X , Y - 1);
return;
}
//4
if (EdgePoints[X - 1, Y - 1] == 2)
{
EdgeMap[X - 1, Y - 1] = 1;
VisitedMap[X - 1, Y - 1] = 1;
Travers(X - 1, Y - 1);
return;
}
//5
if (EdgePoints[X - 1, Y] == 2)
{
EdgeMap[X - 1, Y ] = 1;
VisitedMap[X - 1, Y ] = 1;
Travers(X - 1, Y );
return;
}
//6
if (EdgePoints[X - 1, Y + 1] == 2)
{
EdgeMap[X - 1, Y + 1] = 1;
VisitedMap[X - 1, Y + 1] = 1;
Travers(X - 1, Y + 1);
return;
}
//7
if (EdgePoints[X, Y + 1] == 2)
{
EdgeMap[X , Y + 1] = 1;
VisitedMap[X, Y + 1] = 1;
Travers(X , Y + 1);
return;
}
//8
if (EdgePoints[X + 1, Y + 1] == 2)
{
EdgeMap[X + 1, Y + 1] = 1;
VisitedMap[X + 1, Y + 1] = 1;
Travers(X + 1, Y + 1);
return;
}
//VisitedMap[X, Y] = 1;
return;
}
//Canny Class Ends
}
این کار با یک تابع بازگشتی انجام می شود که آستانه دوگانه را با دو آستانه بالا (Threshold (TH و (Low Threshold (TL و تجزیه و تحلیل 8-اتصال انجام می دهد.
دانلود کد فوق از طریق لینک زیر:


دیدگاه خود را ثبت کنید
تمایل دارید در گفتگوها شرکت کنید؟در گفتگو ها شرکت کنید.