برای پی بردن به این موضوع که کدامیک از دو تکنولوژی CCD یا CMOS بهتر است و تصویر بهتری در اختیار کاربر قرار میدهد، لازم است تا ابتدا نحوه ی عملکرد هرکدام از این تکنولوژی ها را فرا بگیریم :
CCD چطور کار میکند ؟

همانطور که در شکل مشاهده میفرمایید، CCD دارای دو بخش اصلی مجزا از هم می باشد، بخش نارنجی رنگ که پیکسل ها را مشخص میکند و در حقیقت همان فتودیود است و بخش آبی رنگ که ترانزیستورهای مختلف، آی سی سیستم را تشکیل می دهند.
بدلیل جدا بودن فتودیود از ترانزیستورها، امکان جذب نور در این تکنولوژی در حالت حداکثر ممکن میباشد و با توجه به اینکه از یک آی سی جداگانه برای پردازش تصاویر تهیه شده توسط فتودیودها استفاده میشود هم میتوان امکانات بیشتری ( از جمله الگوریتم های حذف نویز، تشخیص چهره، تشخیص حرکت و … ) را به سیستم تصویربرداری اضافه کرد.
CMOS چطور کار میکند ؟

تفاوت اصلی تکنولوژی CMOS با CCD همانطور که در شکل کاملا مشخص می باشد در این است که فتودیودها و ترانزیستورها در تکنولوژی CMOS بر روی یک برد سوار میشوند.
این روش باعث پایین آمدن مصرف انرژی نسبت به CCD و کمترشدن قیمت تمام شده ی محصول تهیه شده با تکنولوژی CMOS می شود ولی با توجه به کیفیت پایین تر و حساسیت به نور کمتر نمیتوان گفت که دوربین هایی که از تکنولوژی CMOS استفاده میکنند کارایی بهتری نسبت به دوربین های مشابه با تکنولوژی CCD دارند.

مقایسه CCD با CMOS :
در شکل بالا تصاویر تهیه شده توسط دو دوربین با لنزها و شرایط نوردهی یکسان توسط CCD و CMOS نمایش داده شده است. همانطور که در شکل ملاحظه می فرمایید تصاویر تهیه شده با CCD از نویز کمتری برخوردار بوهد و رنگ ها شفافیت و واقعیت بیشتری دارند.
بطور کلی اگر بخواهیم این دو تکنولوژی را با هم مقایسه کنیم میتوانیم به موارد زیر توجه کنیم :
• دوربین های CMOS حساسیت به نور کمتری دارند، لذا تصاویر دریافت شده از کیفیت پایینتری نسبت به تکنولوژی همرده در دوربین های CCD برخوردار است.
• دوربین های CMOS حساسیت بیشتری به نویز دارند.
• دوربین های CMOS در هنگام استفاده از سیستم “دید در شب” چون از راهکار “مادون قرمز” استفاده میشود که نور تک رنگ با قدرت کم در محیط وجود دارد، تصاویر مناسبی ارائه نمیدهند.
• دوربین های CMOS ارزانتر از دوربین های CCD میباشند و این به دلیل عدم استفاده از یک بورد جداگانه برای عمل پردازش تصویر می باشد.
• دوربین های CMOS مصرف انرژی کمتری نسبت به دوربین های CCD دارند و درصورتی که شما از سیستم های امنیت تصویری با باتری یا سیستم پشتیبان ( یو پی اس ) استفاده میکنید بکاربردن دوربین های CMOS به صرفه تر است.
• قابلیت های دوربین های CMOS برای تشخیص چهره، حرکت و … پایین تر از دوربین های CCD می باشد.
• دوربین های CCD با سرعت بیشتری عمل Shuttering را انجام می دهند به این معنی که عمل تصویربرداری از اجسام متحرک بهتر و واضح تر انجام می شود.
منبع
مسئله کد گشایی و الگوریتم ویتربی (Viterbi Algorithm)
در این حالت میخواهیم با داشتن دنباله مشاهدات 



یک راه حل این است که محتملترین حالت در لحظه t را بهدست آوریم و تمام حالات را به این شکل برای دنبالهٔ ورودی بهدست آوریم. اما برخی مواقع این روش به ما یک دنبالهٔ معتبر و بامعنا از حالات را نمیدهد. به همین دلیل، باید راهی پیدا کرد که یک چنین مشکلی نداشته باشد.
در یکی از این روشها که با نام الگوریتم Viterbi شناخته میشود، دنباله حالات کامل با بیشترین مقدار نسبت شباهت پیدا میشود. در این روش برای ساده کردن محاسبات متغیر کمکی زیر را تعریف مینماییم.
که در شرایطی که حالت فعلی برابر با i باشد، بیشترین مقدار احتمال برای دنباله حالات و دنباله مشاهدات در زمان t را میدهد. به همین ترتیب میتوان روابط بازگشتی زیر را نیز بهدستآورد.
که در آن
به همین دلیل روال پیدا کردن دنباله حالات با بیشترین احتمال از محاسبهٔ مقدار 

و با شروع از حالت 
مسئله یادگیری
بهطور کلی مسئله یادگیری به این موضوع میپردازد که چگونه میتوان پارامترهای مدل HMM را تخمین زد تا مجموعه دادههای آموزشی به بهترین نحو به کمک مدل HMM برای یک کاربرد مشخص بازنمایی شوند. به همین دلیل میتوان نتیجه گرفت که میزان بهینه بودن مدل HMM برای کاربردهای مختلف، متفاوت است. به بیان دیگر میتوان از چندین معیار بهینهسازی متفاوت استفاده نمود، که از این بین یکی برای کاربرد مورد نظر مناسب تر است. دو معیار بهینهسازی مختلف برای آموزش مدل HMM وجود دارد که شامل معیار بیشترین شباهت (ML) و معیار ماکزیمم اطلاعات متقابل ((Maximum Mutual Information (MMI) میباشند. آموزش به کمک هر یک از این معیارها در ادامه توضیح داده شدهاست.
معیار بیشترین شباهت((Maximum Likelihood (ML)
در معیار ML ما سعی داریم که احتمال یک دنباله ورودی 
با توجه به رابطه فوق در حالت کلی معیار ML به صورت زیر تعریف میشود.
اگر چه هیچ راه حل تحلیلی مناسبی برای مدل 

الگوریتم بام- ولش
این روش را میتوان به سادگی و با محاسبه احتمال رخداد پارامترها یا با محاسبه حداکثر رابطه زیر بر روی 
یکی از ویژگیهای مخصوص این الگوریتم این است که همگرایی در آن تضمین شدهاست. برای توصیف این الگوریتم که به الگوریتم پیشرو- پسرو نیز معروف است، باید علاوه بر متغیرهای کمکی پیشرو و پسرو که قبلاً تعریف شدهاند، متغیرهای کمکی بیشتری تعریف شود. البته میتوان این متغیرها را در قالب متغیرهای پیشرو و پسرو نیز تعریف نمود.
اولین متغیر از این دست احتمال بودن در حالت i در زمان t و در حالت j در زمان t+1 است، که به صورت زیر تعریف میشود.
این تعریف با تعریف زیر معادل است.
میتوان این متغیر را با استفاده از متغیرهای پیشرو و پسرو به صورت زیر تعریف نمود.

متغیر دوم بیانگر احتمال پسین حالت i با داشتن دنباله مشاهدات و مدل مخفی مارکوف میباشد و به صورت زیر بیان میشود.
این متغیر را نیز میتوان در قالب متغیرهای پیشرو و پسرو تعریف نمود.
رابطه بین دو متغیر فوق به صورت زیر بیان میشود.
اکنون میتوان الگوریتم آموزش بام – ولش را با ماکزیمم کردن مقدار بهدستآورد. اگر مدل اولیهٔ ما باشد، میتوانیم متغیرهای پسرو و پیشرو و متغیرهای 

فرمولهای بازتخمین را میتوان بهراحتی به شکلی تغییر داد که با توابع چگالی پیوسته نیز قابل استفاده باشند.
الگوریتم حداکثرسازی امید ریاضی (Expectation Maximization)
الگوریتم حداکثرسازی امید ریاضی یا EM به عنوان یک نمونه از الگوریتم بام – ولش در آموزش مدلهای HMM مورد استفاده قرار میگیرد. الگوریتم EM دارای دو فاز تحت عنوان Expectation و Maximization است. مراحل آموزش مدل در الگوریتم EM به صورت زیر است.
- مرحله مقدار دهی اولیه: پارامترهای اولیه مدل
را تعیین مینماییم.
- مرحله امید ریاضی(Expectation): برای مدل
موارد زیر را محاسبه میکنیم.
مقادیر با استفاده از الگوریتم پیشرو
- مقادیر
و
با استفاده از الگوریتم پسرو
- مرحله ماکزیممسازی (Maximization): مدل
را با استفاده از الگوریتم باز تخمین محاسبه مینماییم.
- مرحله بروزرسانی
- بازگشت به مرحله امید ریاضی
روال فوق تا زمانی که میزان نسبت شباهت نسبت به مرحله قبل بهبود مناسبی داشته باشد ادامه مییابد.
روش مبتنی بر گرادیان
در روش مبتنی بر گرادیان هر پارامتر

که در آن مقدار J با ید مینیمم شود. در این حالت خواهیم داشت.
از آنجا که مینیمم کردن J معادل است با مینیمم کردن


با مشتق گرفتن از رابطهٔ قبل به این نتیجه دست مییابیم:
از آنجا که در رابطهٔ فوق مقدار 


در روش مبتنی بر گرادیان، مقدار 


استفاده از مدل HMM در شناسایی گفتار
بحث شناسایی اتوماتیک گفتار را میتوان از دو جنبه مورد بررسی قرار داد.
- از جنبه تولید گفتار
- از جنبه فهم و دریافت گفتار
مدل مخفی مارکوف (HMM) تلاشی است برای مدلسازی آماری دستگاه تولید گفتار و به همین دلیل به اولین دسته از روشهای شناسایی گفتار تعلق دارد. در طول چندین سال گذشته این روش به عنوان موفقترین روش در شناسایی گفتار مورد استفاده قرار گرفتهاست. دلیل اصلی این مسئله این است که مدل HMM قادر است به شکل بسیار خوبی خصوصیات سیگنال گفتار را در یک قالب ریاضی قابل فهم تعریف نماید.
در یک سیستم ASR مبتنی بر HMM قبل از آموزش HMM یک مرحله استخراج ویژگیها انجام میگردد. به این ترتیب ورودی HMM یک دنباله گسسته از پارامترهای برداری است. بردارهای ویژگی میتواند به یکی از دو طریق بردارهای چندیسازی شده یا مقادیر پیوسته به مدل HMM آموزش داده شوند. میتوان مدل HMM را به گونهای طراحی نمود که هر یک از این انواع ورودیها را دریافت نماید. مسئله مهم این است که مدل HMM چگونه با طبیعت تصادفی مقادیر بردار ویژگی سازگاری پیدا خواهد کرد.
استفاده از HMM در شناسایی کلمات جداگانه
در حالت کلی شناسایی واحدهای گفتاری جدا از هم به کاربردی اطلاق میشود که در آن یک کلمه، یک زیر کلمه یا دنبالهای از کلمات به صورت جداگانه و به تنهایی شناسایی شود. باید توجه داشت که این تعریف با مسئله شناسایی گفتار گسسته که در آن گفتار به صورت گسسته بیان میشود متفاوت است. در این بین شناسایی کلمات جداگانه کاربرد بیشتری به نسبت دو مورد دیگر دارد و دو مورد دیگر بیشتر در عرصه مطالعات تئوری مورد بررسی قرار میگیرند. برای این کاربرد راه حلهای مختلفی وجود دارد زیرا معیارهای بهینهسازی متفاوتی را برای این منظور معرفی شدهاست و الگوریتمهای پیادهسازی شده مختلفی نیز برای هر معیار موجود است. این مسئله را از دو جنبه آموزش و شناسایی مورد بررسی قرار میدهیم.
آموزش
فرض میکنیم که فاز پیش پردازش سیستم دنباله مشاهدات زیر را تولید نماید:
پارامترهای اولیه تمام مدلهای HMM را با یک مجموعه از مقادیر مشخص مقدار دهی مینماییم.
در آغاز این مسئله را برای حالت clamped در نظر بگیرید. از آنجایی که ما برای هر کلاس از واحدها یک HMM داریم، میتوانیم مدل
برای حالت free نیز به مانند حالت قبل میتوان مقدار نسبت شباهت را بهدستآورد.
که در آن 

شناسایی
در مقایسه با آموزش، روال شناسایی بسیار سادهتر است. الگوریتم دنبالهٔ مشاهدات موردنظر را دریافت میکند.
در این حالت نرخ شناسایی به صورت نسبت بین واحدهای شناسایی صحیح به کل واحدهای آموزشی حساب میشود.
برای دریافت اطلاعات بیشتر فایل زیر را دانلود و مشاهده فرمایید.
رمز فایل: behsanandish.com
ML_93_1_Chap15_Hidden Markov Model
مدل مخفی مارکوف (Hidden Markov Model) قسمت 1
مدل مخفی مارکوف (Hidden Markov Model) قسمت 2
مدل مخفی مارکوف (Hidden Markov Model) قسمت 3
مدل مخفی مارکوف (Hidden Markov Model) قسمت 4
انواع مدلهای مخفی مارکوف و HMM پیوسته
همانطور که گفته شد نوع خاصی از HMM وجود دارد که در آن تمام حالات موجود با یکدیگر متصل هستند. لیکن مدل مخفی مارکوف از لحاظ ساختار و اصطلاحاً توپولوژی انواع مختلف دارد. همانطور که گفته شد برای مدل ارگودیک برای تمام i و jها 


در قسمتهای قبل مدلهای HMM برای مجموعه مشاهدات گسسته را مورد بررسی قرار دادیم. اگر چه میتوان با چندیسازی تمام فرایندهای پیوسته را به فرایندهای با دنباله مشاهدات گسسته تبدیل نمود، اما این کار ممکن است باعث افت مدل شود. در مدل HMM پیوسته احتمال قرار گرفتن مشاهدات در یک حالت را با توابع چگالی احتمال نشان میدهند. در این شرایط برای هر حالت i و ورودی O، احتمال مشاهده 
مدل مخلوط گاوسی
مدل مخلوط گوسی یکی از مهمترین روشهای مدل کردن سیگنال است که در واقع شبیه یک HMM یک حالته است که تابع چگالی احتمال آن حالت دارای چندین مخلوط نرمال میباشد. احتمال تعلق بردار آزمایشیd به یک مدل مخلوط گاوسی دارای M مخلوط به شکل زیر بیان میشود:
که در آن 


برای بهدست آوردن پارامترهای مدل GMM، شامل وزن مخلوطهای گاوسی و میانگین و کواریانس توزیعها، از الگوریتم ماکزیمم نمودن امید ریاضی(EM)استفاده میشود. باید توجه داشت که تعداد مخلوطهای گاوسی با تعداد نمونههای موجود آموزشی رابطه مستقیم دارند و نمیتوان با مجموعه دادهای ناچیز یک مدل GMM دارای تعداد بیش از حد از مخلوطها را آموزش داد. در تشکیل و آموزش مدل GMM مانند تمام روشهای تشکیل مدل رعایت نسبت میزان پیچیدگی مدل و نمونههای آموزشی الزامی میباشد.
فرضیات تئوری مدل مخفی مارکوف
برای اینکه مدل مخفی مارکوف از لحاظ ریاضی و محاسباتی قابل بیان باشد فرضهای زیر در مورد آن در نظر گرفته میشود.
۱- فرض مارکوف
با داشتن یک مدل مخفی مارکوف، احتمال انتقال از حالت i به حالت j به صورت زیر تعریف میشود:
به بیان دیگر فرض میشود که حالت بعدی تنها به حالت فعلی بستگی دارد. مدل حاصل از فرض مارکوف یک مدل HMM مرتبه صفر میباشد. در حالت کلی، حالت بعدی میتواند با k حالت قبلی وابسته باشد. این مدل که مدل HMM مرتبه k ام گفته میشود، با استفاده از احتمالات انتقال به صورت زیر تعریف میگردد.
به نظر میرسد که یک مدل HMM از مرتبه بالاتر باعث افزایش پیچیدگی مدل میشود. علیرغم اینکه مدل HMM مرتبه اول متداولترین مدل است، برخی تلاشها برای استفاده از مدلهای دارای مرتبه بالاتر نیز در حال انجام میباشد.
۲- فرض ایستایی (stationarity)
در اینجا فرض میشود که احتمال انتقال در بین حالات از زمان واقعی رخداد انتقال مستقل است. در این صورت میتوان برا ی هر 
۳- فرض استقلال خروجی
در این حالت فرض میشود که خروجی (مشاهدات) فعلی به صورت آماری از خروجی قبلی مستقل است. میتوان این فرض را با داشتن دنبالهای از خروجیها مانند بیان نمود:
آنگاه مطابق با این فرض برای مدل HMM با نام
اگر چه بر خلاف دو فرض دیگر این فرض اعتبار کمتری دارد. در برخی حالات این فرضیه چندان معتبر نیست و موجب میشود که مدل HMM با ضعفهای عمدهای مواجه گردد.
مسئله ارزیابی و الگوریتم پیشرو (forward)
در این حالت مسئله این است که با داشتن مدل 




متغیر پیشرو به صورت یک احتمال از دنباله مشاهدات 

که در آن

با داشتن این رابطه بازگشتی میتوانیم مقدار زیر را محاسبه نماییم.
و آنگاه احتمال 
پیچیدگی محاسباتی روش فوق که به الگوریتم پیشرو معروف است برابر با 
روشی مشابه روش فوق را میتوان با تعیین متغیر پسرو، 

مانند روش پیشرو یک رابطه بازگشتی به شکل زیر برای محاسبه 

که در آن
میتوان ثابت کرد که
آنگاه میتوان با کمک هر دو روش پیشرو و پسرو مقدار احتمال 

مدل مخفی مارکوف (Hidden Markov Model) قسمت 1
مدل مخفی مارکوف (Hidden Markov Model) قسمت 2
مدل مخفی مارکوف (Hidden Markov Model) قسمت 3
مدل مخفی مارکوف (Hidden Markov Model) قسمت 4
کاربردهای مدل مخفی مارکوف
- بازشناسی گفتار
- ترجمه ماشینی
- پیشبینی ژن
- همترازسازی توالی
- تشخیص فعالیت
- تاشدگی پروتئین
- تشخیص چهره
تاریخچه
مدل مخفی مارکوف برای اولین بار در مجموعهمقالات آماری leonard E.Baum و سایر نویسندگان در نیمه دوم دهه ۱۹۶۰ توضیح داده شد. یکی از اولین کاربردهای HMM تشخیص گفتار بوده که در اواسط دههٔ ۱۹۷۰ شروع شد. HMM در نیمهٔ دوم ۱۹۸۰ وارد حوزهٔ آنالیز دنبالههای بیولوژیکی، بهطور خاص DNA شد. از آن پس، کاربرد آن در بیوانفورماتیک گسترش یافت.
انواع مدل مخفی مارکوف
مدل پنهان مارکوف میتواند فرایندهای پیچیده مارکوف را که حالتها بر اساس توزیع احتمالی مشاهدات را نتیجه میدهند، مدل کند. بهطور مثال اگر توزیع احتمال گوسین باشد در چنین مدل مارکوف پنهان خروجی حالتها نیز از توزیع گوسین تبعیت میکنند. علاوه بر این مدل مخفی مارکوف میتواند رفتارهای پیچیدهتر را نیز مدل کند. جایی که خروجی حالتها از ترکیب دو یا چند توزیع گوسین پیروی کند که در این حالت احتمال تولید یک مشاهده از حاصلضرب گوسین انتخاب شدهٔ اولی در احتمال تولید مشاهده از گوسین دیگر به دست میآید.
فرایند مارکوف گسسته
یک سیستم مانند شکل زیر را که در هر لحظه در یکی از حالت متمایز S1,… ,SN است در نظر بگیرید. در زمانهای گسسته و با فواصل منظم، حالت سیستم با توجه به مجموعهای از احتمالات تغییر میکند. برای زمانهای… ,t=۱٬۲ حالت در لحظه t را با qt نشان میدهیم. برای یک توصیف مناسب از سیستم فعلی نیاز به دانستن حالت فعلی در کنار تمام حالات قبلی میباشد. برای یک حالت خاص از زنجیره مارکوف مرتبه اول، توصیف احتمالاتی تنها با حالت فعلی و حالت قبلی مشخص میشود.
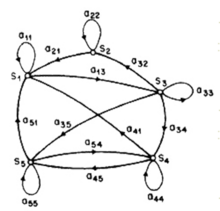


حال تنها فرایندهایی را در نظر میگیریم که در آنها سمت راست رابطه فوق مستقل از زمان است و به همین دلیل ما مجموعهای از احتمالات انتقال بین حالتها را خواهیم داشت.
که در آن احتمال انتقال بین حالات دارای خواص زیر است.
فرایند تصادفی فوق را مدل مارکوف قابل مشاهده میگویند زیرا خروجی مدل مجموعهای از حالات است که قرار گرفتن در آنها متناظر با یک مشاهده میباشد. ما میتوانیم دنباله مشاهدات مورد انتظار خود را تولید کنیم و احتمال وقوع آن در زنجیره مارکوف را محاسبه نماییم. برای مثال با داشتن دنباله مشاهدات 
یکی دیگر از مواردی که مطرح میشود این است که اگر سیستم در حالت


مرتبه مدل مارکوف
۱- مدل مارکوف مرتبه صفر
یک مدل مارکوف از مرتبه صفر هیچ حافظهای ندارد و برای هر t و t’ در دنباله سمبلها، 
۲- مدل مارکوف مرتبه اول
یک مدل مارکوف مرتبه اول دارای حافظهای با طول ۱ میباشد. توزیع احتمال در این مدل به صورت زیر مشخص میشود.
تعریف فوق مانند این است که k مدل مارکوف در مرتبه صفر برای هر 
۳- مدل مارکوف مرتبه m ام
مرتبه یک مدل مارکوف برابر است با طول حافظهای که مقادیر احتمال ممکن برای حالت بعدی به کمک آن محاسبه میشود. برای مثال، حالت بعدی در یک مدل مارکوف از درجه ۲ (مدل مارکوف مرتبه دوم) به دو حالت قبلی آن بستگی دارد.
مثال ۱: برای مثال اگر یک سکه معیوب A داشته باشیم که احتمالات شیر یا خط آمدن برای آن یکسان نباشد، میتوان آن را با یک مدل مارکوف درجه صفر با استفاده از احتمالات (pr(H و (pr(H توصیف نمود.
pr(H)=0.6, pr(T)=۰٫۴
مثال ۲: حال فرض کنید که سه سکه با شرایط فوق در اختیار داریم. سکهها را با اسامی B, A و C نامگذاری مینماییم. آنگاه برای توصیف روال زیر به یک مدل مارکوف مرتبه اول نیاز داریم:
- فرض کنید سکه X یکی از سکههای A یا B باشد.
- مراحل زیر را تکرار میکنیم.
a) سکه X را پرتاب میکنیم و نتیجه را مینویسیم.
b) سکه C را نیز پرتاب میکنیم.
c) اگر سکه C خط آمد، آنگاه سکه X را تغییر میدهیم (A را با B یا B را با A جایگزین میکنیم) و در غیر این صورت تغییری در سکهها نمیدهیم.
انجام روال فوق مدل مارکوف مرتبه اول زیر را نتیجه خواهد داد.
یک پردازش مارکوفی مانند نمونه فوق در طول پیمایش احتمالات، یک خروجی نیز خواهد داشت. یک خروجی نمونه برای پردازش فوق میتواند به شکل HTHHTHHttthtttHHTHHHHtthtthttht باشد.

مدل مخفی مارکوف (HMM)
تا اینجا ما مدل مارکوف، که در آن هر حالت متناظر با یک رویداد قابل مشاهده بود را معرفی نمودیم. در این بخش تعریف فوق را گسترش میدهیم، به این صورت که در آن، مشاهدات توابع احتمالاتی از حالتها هستند. در این صورت مدل حاصل یک مدل تصادفی با یک فرایند تصادفی زیرین است که پنهان است و تنها توسط مجموعهای از فرایندهای تصادفی که دنباله مشاهدات را تولید میکنند قابل مشاهده است.

برای مثال فرض کنید که شما در یک اتاق هستید و در اتاق مجاور آن فرد دیگری سکههایی را به هوا پرتاب میکند و بدون اینکه به شما بگوید این کار را چگونه انجام میدهد و تنها نتایج را به اطلاع شما میرساند. در این حالت شما با فرایند پنهان انداختن سکهها و با دنبالهای از مشاهدات شیر یا خط مواجه هستید. مسئلهای که اینجا مطرح میشود چگونگی ساختن مدل مارکوف به منظور بیان این فرایند تصادفی است. برای مثال اگر تنها مشاهدات حاصل از انداختن یک سکه باشد، میتوان با یک مدل دو حالته مسئله را بررسی نمود. یک مدل مخفی مارکوف را میتوان با تعیین پارامترهای زیر ایجاد نمود:
تعداد حالات ممکن: تعداد حالتها در موفقیت مدل نقش به سزایی دارد و در یک مدل مخفی مارکوف هر حالت با یک رویداد متناظر است. برای اتصال حالتها روشهای متفاوتی وجود دارد که در عمومیترین شکل تمام حالتها به یکدیگر متصل میشوند و از یکدیگر قابل دسترسی میباشند. تعداد مشاهدات در هر حالت: تعداد مشاهدات برابر است با تعداد خروجیهایی که سیستم مدل شده خواهد داشت.
N تعداد حالتهای مدل M تعداد سمبلهای مشاهده در الفبا، اگر مشاهدات گسسته باشند آنگاه M یک مقدار نا محدود خواهد داشت.
![{\displaystyle \ A=[a_{ij}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c2e5be58535cfa69a95badb38fd3533bfb6235e)
که در آن 
برای حالات مدل ارگودیک برای تمامi وjها مقدار

توزیع احتمال مشاهدات: یک توزیع احتمال برای هر یک از حالتها
که در آن 

اگر مشاهدات به صورت پیوسته باشند، باید به جای احتمالهای گسسته از یک تابع چگالی احتمال پیوسته استفاده شود. معمولاً چگالی احتمال به کمک یک مجموع وزندار از M توزیع نرمال μ تخمین زده میشود.
که در آن 



توزیع احتمال حالت آغازین

به این ترتیب ما میتوانیم یک مدل مخفی مارکوف با توزیع احتمال گسسته را با استفاده از سهگانه زیر مشخص نماییم.
همچنین یک مدل مخفی مارکوف با توزیع احتمال پیوسته به صورت زیر نشان داده میشود.
مدل مخفی مارکوف (Hidden Markov Model) قسمت 1
مدل مخفی مارکوف (Hidden Markov Model) قسمت 2
مدل مخفی مارکوف (Hidden Markov Model) قسمت 3
مدل مخفی مارکوف (Hidden Markov Model) قسمت 4
فناوری فشرده سازی تصویر چگونه عمل می کند؟
فشرده سازی تصویر یکی از تکنولوژی هایی است که در فضای رسانه و رایانه بسیار مفید و با اهمیت است و با استفاده از آن می توان حجم تصاویر را تا حد خوبی کاهش داد. اهمیت از این تکنولوژی زمانی مشخص می شود که حجم عکس برای شما مهم باشد و کاهش چند درصد از حجم آن نیز برای شما غنیمت باشد. در این صورت است که به فناوری و تکنولوژی فشرده سازی تصاویر اهمیت خواهید داد.
اگر از شبکه های اجتماعی و اینترنت برای ارسال یا دریافت فایل و تصویر استفاده کرده باشید حتما متوجه شده اید که فایل های حجیم با چه سختی ارسال یا دریافت می شوند. حال تصور کنید روشی وجود داشته باشد که حجم این فایل ها (مخصوصا تصاویر) را کاهش می دهد بدون این که از کیفیت آنها کاسته شود. در این صورت حتما تمایل دارید از این روشها استفاده نمایید.
چرا باید تصاویر را فشرده سازی کرد؟
در ابتدا شاید این سوال بوجود آید که چرا باید تصاویر و یا فایل ها را فشرده سازی کرد؟ در پاسخ به این سوال باید گفت که اصلی ترین دلیل فشرده سازی فایل ها و تصاویر کاهش حجم آن می باشد. این موضوع در ارسال و دریافت فایل ها بسیار تاثیرگذار است و زمان لازم برای آن را کاهش می دهد. همچنین باعث می شود زمان بارگذاری وب سایت ها نیز کاهش یابد و باعث می شود مجموع حجم مصرف شده از حافظه رایانه شما کمتر شود. در بعضی حتی امکان ارسال فایل های حجم بالا وجود ندارد و به ناچار باید حجم فایل را کاهش داد که در این صورت فشرده سازی تصویر روش مناسبی می باشد. خب همین چند دلیل برای فشرده سازی تصاویر کافیست و باعث می شود افراد از این فناوری استفاده نمایند.
فشرده سازی تصویر چیست؟
تکنولوژی فشرده سازی تصویر در حقیقت فشرده سازی اطلاعات داخل تصویر می باشد. در این روش افزونگی محتویات داخل تصویر کاهش می یابد و باعث بهینه سازی شدن تصویر می شود که نتیجه آن فشرده یا کم حجم شدن تصویر می باشد. به این صورت که بخش های اضافی و زاید (افزونگی) موجود در اطلاعات تصویر حذف می شوند و همین باعث بهینه شدن و کم حجم شدن تصویر می شود.
برای فشرده سازی تصاویر روشهای مختلف با الگوریتم های مختلفی وجود دارد که هر یک از این روشها در نهایت منجر به کاهش حجم تصویر می شود. اما در نوع انجام با یکدیگر متفاوت هستند و بسته به روش مورد استفاده مقدار حجم کاهش یافته نیز متغیر خواهد بود.
روشهای فشرده سازی تصویر
برای فشرده سازی یا بهینه سازی تصویر دو روش از نظر نتیجه وجود دارد. یکی فشرده سازی بدون اتلاف (Lossless) که در آن کیفیت تصویر کاهش نمی یابد اما ضریب فشرده سازی کمتری دارد و مقدار کمتری از حجم عکس کاهش می یابد. دیگر روش بااتلاف (Lossy) است که نسبت به نوع اول فشرده سازی و کاهش حجم بیشتری به دنبال دارد. اما کاهش کیفیت نیز به همراه خواهد داشت. بسته به نیازی که از تصویر یا فشرده سازی دارید باید نوع فشرده سازی را انتخاب نمایید. به عنوان مثال برای فشرده سازی نقشه ها، تصاویر پزشکی، تصاویر اسکن و تصاویری که کیفیت آنها اهمیت بالایی دارد باید از روش بدون اتلاف استفاده کرد تا ضمن کاهش نسبی حجم فایل کیفیت آن آسیب نبیند. همچنین برای فشرده سازی تصاویر شبکه های اجتماعی، وب سایت ها، عکس های طبیعت و مناظر و … می توان از روش بااتلاف استفاده کرد. زیرا در این نوع تصاویر کیفیت اهمیت بالایی ندارد و استفاده از این روش می تواند باعث کاهش حجم بیشتری از تصویر باشد.
فشرده سازی بدون اتلاف
این روش را روش فشرده سازی بازگشت پذیر نیز می گویند. زیرا با استفاده از این روش امکان بازگردانی تصویر فشرده شده به تصویر اصلی وجود دارد. این روش ضریب فشرده سازی کمتری دارد و کیفیت تصویر را کاهش نمی دهد. برای فشرده سازی عکس ها با این روش الگوریتم های مختلفی وجود دارند که نتیجه بالا را به دست می دهند. رایج ترین الگوریتم حذف محتواهای تکراری با روشی خاص است. به این صورت سیستم از عبارات و متون تکراری فاکتور می گیرد و محتواهای اضافی را حذف می کند. برای درک بهتر موضوع به این مثال توجه کنید. تصر کنید محتوای ما «whatisimage whatisimage2 whatisimage3» باشد. اگر بخواهیم این متن را با روش فوق فشرده سازی کنیم لازم است از عبارت تکراری «whatisimage» فاکتور بگیریم و بقیه آنها را حذف نماییم. نتیجه به صورت «w (w)2 (w)3» در می آید. در این روش عبارت «(w)» به جای «whatisimage» قرار گرفته است و همین باعث شده طول متن مورد نظر تا حد زیادی کاهش یابد.
البته روش کمی پیچیده تر از این است و توسط رایانه انجام می شود. اما کلیت آن به این صورت می باشد. در تصاویر نیز به همین صورت است. فایل تصویر در رایانه حاوی مقدار زیادی کد به زبان رایانه است که پس از اجرا توسط کامپیوتر نتیجه آن که یک تصویر است نمایش داده می شود. بنابراین با این روش فشرده سازی می توان کدهای تصویر را بهینه کرد و از بخش های تکراری آن فاکتورگیری نمود که نتیجه آن کاهش حجم تصویر و فشرده شدن آن می باشد.
فشرده سازی بااتلاف
روش دیگر فشرده سازی بااتلاف یا فشرده سازی بازگشت ناپذیر می باشد که در آن کیفیت تصویر کاهش می یابد و بر خلاف روش قبلی امکان بازگردانی تصویر فشرده شده به تصویر اصلی وجود نخواهد داشت. در حقیقت نقطه ضعف اصلی این روش از دست رفتن اطلاعات و داده های موجود در تصویر طی فرایند می باشد. به همین دلیل استفاده از آن برای تصاویر مهم و لازم برای آرشیو اطلاعاتی مناسب نمی باشد.

البته باید توجه داشت که این روش یک امتیاز مهمی دارد و آن ضریب بالای فشرده سازی می باشد. یعنی حجم کاهش یافته از تصویر طی این فرایند بیشتر است و در نتیجه تصویر فشرده شده حجم کمترین خواهد داشت.
از این روش در شبکه های اجتماعی، پیام رسان ها، نرم افزارهای ارسال فایل، وب سایت ها و … که حجم تصویر بر کیفیت آن ارجحیت دارد استفاده می شود.
ابزارهای فشرده سازی عکس
حال با توجه به مطالب مذکور اگر تمایل دارید تصاویر خود را فشرده سازی کرده و حجم آنها را کاهش دهید می توانید از نرم افزارهای مربوطه و وبسایت های سرویس دهنده در این زمینه استفاده نمایید. نرم افزار و وبسایت های مختلفی برای فشرده سازی تصویر وجود دارند که با جستجو در اینترنت به راحتی آنها را پیدا خواهید کرد. اگر از سرویس های آنلاین استفاده کنید لازم است ابتدا تصاویر خود را در بخش مربوطه وب سایت بارگذاری نموده و سپس عملیات فشرده سازی را آغاز نمایید. پس از انجام عملیات لینک دانلود تصویر فشده شده در اختیار شما قرار خواهد گرفت و می توانید آن را دانلود کنید.
بدی این روش این است که شما باید ابتدا فایل اصلی خود را که احتمالا حجم بالایی نیز دارد ارسال کنید تا وب سایت سرویس دهنده عملیات فشرده سازی را انجام دهد. برای تصاویر حجم بالا و یا تصاویر خصوصی و شخصی این روش اصلا مناسب نیست و عملا امکان ارسال فایل وجود ندارد. به جای آن بهتر است از نرم افزارهای فشرده سازی تصویر استفاده کنید. Advanced JPEG Compressor و PicShrink دو برنامه فشرده سازی مخصوص دسکتاپ هستند که با استفاده از آنها می توانید تصاویر حجم بالا را نیز فشرده نمایید. مزیت استفاده از نرم افزار این است که دیگر نیازی به ارسال تصاویر و فایل ها به وب سایت سرویس دهنده وجود ندارد و می توان عملیات را در رایانه شخصی انجام داد.
انواع روشهای فشرده سازی تصویر
فشرده سازی تصویر یکی از روشهای کاهش حجم آن می باشد و برای ذخیرهسازی عکس ها از این روش استفاده می شود تا حجم اطلاعات و حافظه مصرفی تا جای ممکن کاهش پیدا کند. برای انجام این کار دو روش بااتلاف و بدون اتلاف کیفیت تصویر وجود دارد که به وسیله الگوریتم های مختلف رایانه ای انجام می شود. در ادامه برخی از روشهای فشرده سازی تصاویر را ذکر خواهیم کرد.
در روشهای فشرده اگر بخواهیم درصد فشرده سازی بیشتر باشد باید قبول کنیم که بخشهایی از اطلاعات و دادههای موجود در تصویر کنار گذاشته شود و به عبارت دیگر حذف شود. در این صورت مشاهده می شود که تصویر فشرده شده تا حدودی کیفیت خود را از دست داده است. اما در روشهای بدون اتلاف چنین نیست و کیفیت تصویر تغییری نمی کند اما در عوض مقدار فشرده سازی و کاهش حجم فایل در این روشها پایین تر می باشد.
در روش فشرده سازی تصویر میزان کنار گذاشتن یا حذف بخشهای از تصویر به وسیله ضریب یا نسبت فشردهسازی معین می شود. هرچه این ضریب بیشتر باشد مقدار فشرده سازی و مقدار حذف اطلاعات بیشتر خواهد بود و در نهایت کیفیت تصویر نیز بیشتر کاهش می یابد. اما باید گفت که در این روش ذخیرهسازی و انتقال داده ها بسیار راحت تر بوده و عملیات فشرده سازی تصویر سریع تر انجام می شود.
امروزه برای فشردهسازی عکس روشهای مختلفی وجود دارد که بسیار پیشرفته هستند. فشردهسازی تصویر از اصلی مهم پیروی می کند و آن این است که چشم انسان فاصله بین دو نقطه کوچک در تصویر را تقریبا یکسان می بیند. بر همین اساس در روشهای مختلف فشرده سازی از این اصل استفاده کرده و طیف خاصی از رنگ ها که توسط چشم انسان قابل تشخیص نمی باشد را حذف می کنند.
روشهای فشرده سازی تصویر
اما پس از توضیحات ابتدایی برویم سر اصل موضوع یعنی روشهای فشرده سازی تصویر. به طور کلی ۵ روش فشرده سازی تصویر (JPEG، MPEG، MP3، MPEG2، MPEG) مد نظر ما می باشد که یک یک آنها را ذکر کرده و توضیح می دهیم.
روش JPEG
این فرمت مخفف عبارت JOINT PHOTOGRAPHIC EXPERT GROUP و به معنی «گروه مشترک کارشناسان گرافیک» است. از این نام برای نوعی فشرده سازی تصویر نیز استفاده شده است. روش JPEG اولین و البته ساده ترین روش فشرده سازی تصویر می باشد که جهت فشردهسازی تصاویر گرافیکی استفاده ایجاد شده است.

از این روش همچنین جهت فشردهسازی تصاویر متحرک نیز استفاده شد. برای دستیابی به این هدف تصاویر مورد نظر فریم به فریم فشرده میشدند. اما برای حل این مشکل روش دیگری به نام MOTION JPEG به معنی «JPEG متحرک» ابداع شد که از آن جهت ارتباط دادن تصاویر فریم شده به هم و ساخت یک عکس متحرک استفاده شد.
روش MPEG
نام فرمت MPEG مخفف عبارت MOVING PICTURE EXOERT GROUP و به معنی «گروه کارشناسان تصویر متحرک» می باشد. روش مذکور در ابتدا آن داده های تصویری را با سرعت حدود ۵ مگابیت در ثانیه انتقال می داد که در نهایت منجر به ایجاد تصاویر ویدئویی میشد. با این روش از فشرده سازی تصاویر امکان ذخیره سازی تصاویر متحرک برای ۷۰ دقیقه و به اندازه ۶۵۰ مگابایت فراهم بود. در روش MPEG بیت (Bit) های داده به صورت سریالی ارسال میشوند که در کنار آنها بیتهای کنترل و هماهنگکننده نیز ارسال می شوند که مکان و نوع جاگذاری بیتهای اطلاعاتی را برای ثبت اطلاعات صدا و تصویر تعیین می کند. البته روش کار کمی پیچیده تر از این است که توسط رایانه انجام می شود.
روش MPEG2
در این روش که MPEG2 نام دارد از ضریب فشردهسازی بالاتری نسبت به روشهای پیشین استفاده می شود. در این روش امکان بررسی داده ها ۱۵ مگابیت در ثانیه وجود دارد و از آن در DVD ها استفاده می شود. لازم به ذکر است که در روش MPEG2 هر فریم (Frame) تصویر شامل چندین سطر از اطلاعات دیجیتالی می باشد که با روشهای پیشرفته جایگذاری می شوند.
روش MPEG-4
از این روش در تجهیزاتی استفاده می شود که با انتقال کند یا سریع اطلاعات فعالیت می کنند. در این روش توانایی جبران خطا و ارائه کیفیت بالای تصویر وجود دارد. موضوع جبران خطا در مورد رایانه، تلفن همراه و شبکه اهمیت بالایی دارد که در این روش مدنظر گرفته شده است. به عنوان مثال در شبکه های کامپیوتری تصویر مورد نظر باید برای کاربران دارای مودم کند یا سریع به خوبی نمایش داده شود. در این صورت استفاده از روش MPEG-4 مناسب می باشد. همچنین از این روش در دوربینهای تلویزیونی نیز استفاده می شود.
روش MPEG-4 کاربرد فراوان دارد که نمونه آن در فیلم صحنه بازی تنیس است. در این حالت می توان صحنه را به دو مولفه بازیکن و زمین بازی تقسیم کرد که در آن زمین بازی دائما ثابت می باشد و در تمام تصاویر تکرار می شود. اما بازیکن همواره در حال حرکت می باشد. در این روش پهنای باند اشغالی بسیار کاهش می یابد و با روشهای پیشرفته حجم فایل ها کاهش می یابد.
لازم به ذکر است که علاوه بر این روشها اخیرا روش جدیدی توسط شرکت گوگل ابداع شده که می تواند حجم تصاویر را تا حد زیادی کاهش دهد. گفته می شود استفاده از این روش کاربران شاهد کاهش ۳۵ درصدی حجم تصویر خواهند بود.
در ادامه مطالعه فایل های زیر می تواند کمک کننده باشد:
الگوریتم های فشرده سازی بدون اتلاف
رمز فایل: behsanandish.com
رمز فایل: behsanandish.com
رمز فایل: behsanandish.com
فشرده سازی تصویر (Image Compression)، کاربردی از فشرده سازی اطلاعات در تصاویر دیجیتال است. هدف از آن کاهش افزونگی (redundancy) محتویات تصویر است برای ذخیره کردن یاانتقال اطلاعات به شکل بهینه.
فشرده سازی تصویر میتواند به صورت بی اتلاف (Lossless) و با اتلاف (Lossy) صورت گیرد. فشرده سازی بی اتلاف برای بعضی تصاویر مثل نقشه های فنی و آیکونها ترجیح داده میشود، به این دلیل که فشرده سازی با اتلاف خصوصاً وقتی برای نرخ بیتهای پایین استفاده شود به کیفیت تصویر لطمه میزند. روشهای فشرده سازی بی اتلاف همچنین ممکن است برای محتویات پر ارزش مثل تصاویر پزشکی یا تصاویر اسکن شده برای بایگانی شدن نیز ترجیح داده شوند. روش با اتلاف مخصوصاً برای تصاویر طبیعی مناسب است که از دست رفتن کیفیت برای دست یافتن به کاهش نرخ بیتقابل توجه باشد.
روشهای فشرده سازی بدون اتلاف عکسها عبارتند از
– کدگذاری بر اساس طولِ ران (run-length encoding)، استفاده شده در روشهای پیشفرض در dcx و یکی از امکانات TIFF ,TGA ,BMP
– entropy coding
– الگوریتمهای مطابق واژهنامه مثل lzw استفاده شده در GIF,TIFF
– کاهش اعتبار (deflation) استفاده شده در TIFF ,MNG ,PNG
روشهای فشرده سازی پراتلاف عبارتند از
کاهش فضای رنگی
کاهش فضای رنگی برای رنگهایی که بیشتر در عکس استفاده شدهاند. رنگی که انتخاب شده در پالت رنگ در بالای عکس فشرده شده مشخص میشود. هرپیکسل فقط به شاخص رنگ در پالت رنگ اشاره داده میشود.‘
chroma subsampling
این روش براساس این واقعیت است که چون چشم انسان تغییرات مکانی روشنایی را سخت تر از رنگ درک میکند به وسیلهٔ میانگینگیری یا حذف کردن برخی از اطلاعات رنگ تابی یک عکس عمل فشرده سازی صورت گیرد.
تغییر شکل دادن کدگذاری (transform coding)
این روش بطور عادی بیشترین استفاده را دارد.
fractal compression
بهترین کیفیت عکس در یک نرخ بیت (یا نرخ فشرده سازی) معین هدف اصلی از فشرده سازی عکس است.
به هر حال ویژگیهای مهم دیگری از رویههای فشرده سازی عکس وجود دارد که عبارتند از: ‘
مقیاس پذیری (scability)
بهطور کلی به کاهش کیفیت حاصل شده در اثر دستکاری گروه بیتی یا فایل گفته میشود. (بدون بازیابی). نامهای دیگر برای مقیاس پذیری،progressive coding یا embedded biststream است. با وجود خلاف واقعی بودنش مقیاسپذیری نیز میتواند در رمز گذارهای (codec) بدون اتلاف یافت شود. مقیاسپذیری خصوصاَ برای پیش نمایش عکسها در حال دریافت کردن آنها یا برای تهیه کیفیت دستیابی متغیر در پایگاههای داده مفید است.
انواع مختلف مقیاس پذیری عبارتند از :
کیفیت مترقی(progressive quality)
یا لایه مترقی (layer progressive) گروه بیتی پی در پی عکس را از نو میسازد.
وضوح مترقی (progressive resoloution)
ابتدا یک عکس وضوح پایین را کدگذاری می کند سپس تفاوتهای وضوح بالاتر را کدگذاری میکند.
مؤلفه مترقی (progressive component)
ابتدا رنگ را کدگذاری میکند.
ناحیه
جذاب کدگذاری (region of interest coding) نواحی خاصی از عکس باکیفیت بالاتری نسبت به سایر نقاط کد گذاری میشوند و میتواند با مقیاسپذیری (کدگذاری ابتدایی یک بخش و دیگران بعداً) ترکیب شود.
اطلاعات
غیر نمادین(meta information) دادههای فشرده شده میتوانند شامل اطلاعاتی در رابطه با عکس باشد که میتوان برای طبقهبندی کردن، جستجو یا بررسی عمومی عکس از آنها استفاده کرد. مانند اطلاعاتی که میتوانند شامل رنگ و الگو و پیش نمایش کوچکتر عکسها و اطلاعات خالق و کپی رایت باشد.
قدرت
پردازش(processing power) الگوریتمهای فشرده سازی اندازههای متفاوتی از قدرت پردازش را برای کدگذاری و کدگشایی درخواست میکنند. بعضی از الگوریتمهای فشردهسازی عالی قدرت پردازش بالا میخواهند.
کیفیت
روش فشرده سازی اغلب به وسیلهٔ سیگنال ماکزیمم به نسبت پارازیت (peak signal-to-noise ratio) اندازهگیری می شوند. اندازه پارازیتها نشان دهند؟ فشرده سازی پراتلاف عکس است به هر حال قضاوت موضوع گرایانه بیننده همیشه بیان کنند؟ اهمیت اندازهگیری است.
Jpeg2000
Jpeg2000 یک استاندارد فشرده سازی عکس براساس wavelet (wavelet-based) است؛ و در سال 2000 بهوسیله کمیته Joint Photographic Experts Group با نیت جایگزین کردن با استاندارد اصلیJpegکه براساس تغییر گسسته(discrete cosine transform-based) است (محصول سال1991) تولید شدهاست. jpeg2000 زمان بیشتری را برای عملیات باز کردن فشردگی نسبت به JPEG طلب میکند.
اثبات از بالا به پایین محصولات فشرده سازی JPEG 2000: شمارهها نشاندهنده ضریب تراکم استفاده شدهاست.برای مقایسه بهتر شکل بدون مقیاس را نگاه کنید. محصولات JPEG 2000 به فرم JPEG متفاوت به نظر میرسند و یک جلوه صیقلی روی عکس وجود دارد و برای نمایان شدن سطوح فشرده سازی بالاتری اختیار می کنند. اغلب یک عکس گرفته شده میتواند به اندازه اندازه فایل اصلی خود(bitmapفشرده نشده) بدون متحمل شدن اثر نمایان شدن فشرده شوند
منبع
فشرده سازی با اتلاف داده و بدون اتلاف داده
بسیاری از افراد احساس میکنند که تنها باید از فرمتهای تصاویری استفاده شود که از تکنولوژی فشرده سازی بدون اتلاف داده بهره میبرند. این نوع فشرده سازی برای بسیاری از تصاویر مناسب است اما در بسیاری از موارد نیازی به آن نیست. استفاده از این نوع فشرده سازی به این معناست که همه دادهها از فایل اولیه حفظ شوند اما فشرده سازی با اتلاف داده برخی دادهها را از فایل اولیه حذف میکند و تصویر را با حجم کم ذخیره میکند. در فشرده سازی با اتلاف داده شما میتوانید بگویید نرخ فشرده سازی تصاویر چقدر باشد و چه میزان از دادهها در نظر گرفته نشود.
فشرده سازی بدون اتلاف داده
روشهای کمی برای فشرده سازی بدون اتلاف داده وجود دارد. روش اولکدگذاری طول اجرا (run-length encoding) است که برای فایلهای BMP استفاده میشود. این روش دادههای متوالی با مقادیر یکسان را میگیرد و آنها را با یک متغیر count که بیانگر طول دادههای یکسان است، ذخیره میکند. این روش برای فایلهای گرافیکی مناسب است زیرا مقادیر داده یکسان بسیاری دارند.

روش دیگر فشرده سازی بدون اتلاف داده، DEFLATE نام دارد که برای تصاویر PNG نیز استفاده میشود. این روش از ترکیب الگوریتم کدینگ هافمن و LZ77 ساخته شده است. از این روش در فشرده سازی gzip و ZIP نیز استفاده میشود. الگوریتم Lempel-Ziv-Welch یا LZW هم یکی دیگر از روشهای فشرده سازی است بدون اتلاف داده است که روی دادهها یک آنالیز ساده و محدود انجام میدهد. از این روش در فرمتهای TIFF و GIF استفاده میشود.
فشرده سازی با اتلاف داده
روشهای فشرده سازی با اتلاف داده محدود هستند، برخی از آنها با روشهای بدون اتلاف داده هم ترکیب میشوند تا فایلهایی با اندازه کوچکتر ایجاد کنند. یکی از این روشها، کاهش فضای رنگ تصویر به متداولترین رنگهای داخل تصویر است. از این روش برخی اوقات در فرمت تصاویر PNG و GIF استفاده میشود.

یک روش دیگر، تبدیل رمزگذاری (Transform encoding) است که برای تصاویر JPEG استفاده میشود. در این روش تصاویر با روش DCT یا تبدیل کسینوس گسسته به بلوکهایی تقسیم میشوند و در نهایت تصویری ایجاد میکنند که رنگهایی کمتر از تصویر اولیه داشته باشد.
نمونهبرداری کروما (Chroma subsampling) نام روش دیگری است که بر مبنای این اصل عمل میکند: «چشم انسان تغییرات در روشنایی را سختتر از تغییر رنگ متوجه میشود.» نمونهبرداری کروما اطلاعات روشنایی را نگهمیدارد و برخی از اطلاعات رنگ را حذف میکند. از این روش در تصاویر JPEG و برخی الگوریتمهای کاهش حجم ویدئو استفاده میشود.
انواع مختلف فایلها
در این مقاله سه فرمت مشترک در طراحی وب یعنی PNG ،JPEG و GIF را معرفی میکنیم. غیر از این سه، تعداد زیادی فرمت دیگر هم وجود دارند که از روشهای فشرده سازی استفاده میکنند، مثل: TIFF ،PCX ،TGA و غیره.
فرمت GIF
GIF یا فرمت تبادل گرافیکی (Graphics Interchange Format) در سال ۱۹۸۷ بهوسیله CompuServe معرفی شد و یک فرمت تصویربرداری است. این فرمت تا ۸ بیت در هر پیکسل را پشتیبانی میکند، یعنی یک تصویر میتواند تا ۲۵۶ رنگ RGB مختلف داشته باشد. یکی از بزرگترین ویژگیهای این فرمت توانایی ایجاد تصاویر متحرک است.

فرمت JPEG
JPEG یا Joint Photographic Experts Group فرمتی برای تصاویر است که از فشرده سازی با اتلاف داده استفاده میکند. یکی از بزرگترین مزیتهای JPEG این است که به طراح اجازه میدهد مقدار فشرده سازی را به میزان لازم تنظیم کند. این کار نتیجه بهتری درباره کیفیت و اندازه مناسب به دست میدهد. چون JPEG از فشرده سازی با اتلاف داده استفاده میکند، تصاویری که با این فرمت ذخیره میشوند مصنوعی به نظر میرسند و میتوان هاله نور عجیبی در قسمتهای خاصی از آنها دید. همچنین در بسیاری از قسمتهای یک تصویر میتوان کنتراست شدیدی بین رنگها مشاهده کرد.

فرمت PNG
PNG یا Portable Network Graphics یک فرمت تصویر است که از فشرده سازی بدون اتلاف داده استفاده میکند و برای جایگزین شدن فرمت GIF ایجاد شده است. این فرمت برای مدت طولانی در اینترنت اکسپلورر پشتیبانی نمیشد که به همین دلیل فرمتهای JPEG و GIF متداولتر شدند؛ اگرچه در حال حاضر PNG در همه مرورگرها پشتیبانی میشود. یکی از بزرگترین مزیتهای PNG این است که از تنظیمات متفاوت شفافیت (transparency)، مانند شفافیت کانال آلفا (alpha channel transparency)، پشتیبانی میکند.

انتخاب یک فرمت فایل مناسب
هر کدام از فرمتهایی که در بالا ذکر شد، برای انواع متفاوتی از تصاویر مناسب هستند. انتخاب فرمت مناسب منجر به کیفیت بالاتر و اندازه فایل کوچکتر میشود. انتخاب یک فرمت اشتباه به این معناست که تصاویر شما کیفیت متناسبی با حجمشان ندارند.
برای تصاویر گرافیکی ساده مانند لوگوها یا ترسیم خطوط، فرمت GIF بهتر کار میکند زیرا GIF پالت رنگ محدودی دارد. اگر پیچیدگی بیشتر باشد بهتر است از فرمت دیگری استفاده شود.

برای تصاویر با گرادیان، فرمت GIF مناسب نیست. در این موارد فرمت JPEG هنگامی مفید است که تصویر کنتراست شدیدی نداشته باشد. برای تصاویری با کنتراست بالا یا تصاویر شفاف، فرمت PNG بهترین فرمت است. در اغلب موارد اندازه تصاویر PNG از JPEG بزرگتر است. توجه کنید که فایلهای PNG از روش بدون اتلاف داده استفاده میکنند و کیفیت تصویر اولیه حفظ میشود.
در زیر به طور خلاصه، فرمت مناسب برای انواع تصویر را مرور میکنیم:
فرمت GIF
اگر در تصویری، انیمیشن، رسم خط یا تصویر گرافیکی ساده نیاز باشد، GIF بهترین گزینه است اما برای تصاویر گرادیان این فرمت مناسب نیست.
فرمت JPEG
برای اغلب تصاویر دوربین که کنتراست بالا ندارند یا برای بازیها و فیلمها این فرمت مناسب است. فرمت JPEG برای تصاویر دارای کنتراست بالا یا جزئیات بالا مناسب نیست، به طور مثال برای دیاگرام یا اینفوگرافیک. همچنین برای تصاویر گرافیکی ساده (به دلیل حجم بالا) بهتر است از فرمت GIF استفاده شود.
فرمت PNG
برای تصاویر حاوی خطوط، تصاویر دارای کنتراست شدید، تصاویر دارای شفافیت (transparency)، دیاگرامها، اینفوگرافیکها و اسکرینشاتها، فرمت PNG مناسب است. این فرمت برای تصاویر با کنتراست پایین، به دلیل افزایش حجم فایل، توصیه نمیشود.
فشرده سازی در پرینت تصاویر
آنچه در بالا گفته شد مربوط به انتخاب فرمت مناسب برای فشرده سازی تصاویر در طراحی وب بود ولی هنگام پرینت گرفتن داستان متفاوت است. الگوریتم فشرده سازی با اتلاف داده برای پرینت گرفتن مناسب نیست و در صورت استفاده، کیفیت افت فاحشی خواهد کرد. برای مثال یک تصویر JPEG ممکن است در مانیتور خوب نمایش داده شود اما هنگام چاپ افت کیفیتش نامطلوب باشد.
به منظور پرینت تصاویر فرمت TIFF یا Tagged Image File Format اغلب بهترین گزینه است. در این حالت باید از فرمتهایی (مانند LZW) استفاده کرد که فشرده سازی بدون اتلاف داده به حساب میآیند.
منبع
افزایش کنتراست با یکنواخت سازی هیستوگرام
امروزه روشهای بهبود تصویر بسیاری در حال استفاده هستند. یکی از ایده ها بهبود کنتراست تصویر است. یکی از روش های افزایش کنتراست تصویر با کیفیت پایین، تکنیک یکنواخت سازی هیستوگرام است. بطوریکه مقادیر سطوح خاکستری تصویر را بنحوی تغییر میدهد تا کل بازه ممکن را تسخیر کند و ایده اساسی آن نگاشت مقادیر شدت سطوح روشنایی از طریق یک تابع توزیع انتقال است.
یکنواخت سازی هیستوگرام موجب میشود کنتراست تصویر نسبت به حالت اولیه آن بیشتر شود که این به معنای بهبود کیفیت تصویر و افزایش دقت پردازش های بعدی است. اگرچه این روش قادر به افزایش کنتراست تصویر است اما تصویر حاصل معمولا دارای بهبود غیر طبیعی و اشباع شدت میباشد، همچنین در مشخص نمودن مرزها و لبه های بین اشیا مختلف قدرتمند است ولی ممکن است باعث کاهش جزئیات محلی شود.
فرض کنید یک تصویر خاکستری با مقادیر سطوح روشنایی r در بازه [0,1] وجود داشته باشد، یک تابع تبدیل مانند T بر روی این تصویر بصورت (s=T(r قابل تعریف است.
به منظور یکنواخت سازی هیستوگرام، تبدیلی مانند T باید دارای دو خاصیت باشد:
- این تابع تبدیل بصورت یکنوا صعودی باشد
- بازای r در بازه [0,1] مقادیر T(r) نیز در بازه [0,1] قرار گیرند.
این شروط تضمین میکنند که دامنه خروجی با ورودی یکی باشد، و همچنین نگاشتی یک به یک باشد و مانع ایجاد ابهام شود.
یک ایده برای تابع تبدیل (s=T(r با فرض پیوسته در نظر گرفتن تابع توزیع احتمال که خروجی یکنواخت تولید کند استفاده از رابطه زیر است.
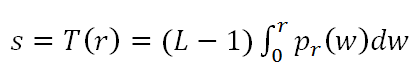
با توجه به تابع یکنواخت ساز فوق و در نظر گرفتن هیستوگرام نرمال شده تصویر در حالت گسسته میتوان تابع تبدیلی که هیستوگرام را یکنواخت کند به شکل زیر بیان کرد:

که در آن MN تعداد کل پیکسلها در تصویر، nk تعداد پیکسلهایی که شدت روشنایی rk دارند و L تعداد سطوح ممکن شدت روشنایی در تصویر است. در واقع ابتدا باید هیستوگرام نرمال شده و سپس هیستوگرام تجمعی تصویر ورودی را محاسبه نمود و نهایتا اعداد را به بازه [0,L-1] انتقال داد و با نگاشت هر پیکسل در تصویر ورودی با شدت روشنایی rk به یک پیکسل متناظر با شدت روشنایی sk تصویر خروجی که دارای هیستوگرامی متعادلتر شده است را بدست آورد.
بعنوان نمونه نتیجه این عملیات را در تصویر زیر میبینید که تصویر ورودی اولیه دارای هیستوگرامی با مقادیری در محدوده خاص و بصورت نا یکنواخت است در حالی که هیستوگرام تصویر حاصل نسبتا یکنواخت تر است و نتیجه کار بهبود کنتراست و بهبود جلوه بصری در تصویر خروجی است

نکته ای که در انتها قابل ذکر است اینکه هیستوگرام تصویر یکنواخت شده مستقل از هیستوگرام اولیه آن است، بدین معنی که اگر یک تصویر با روشنایی های مختلف داشته باشیم (روشن تر یا تیره تر) پس از اعمال الگوریتم یکنواخت سازی، هیستوگرام آن ها یکسان خواهند بود.
منبع
بهبود کنتراست تصاویر رقومی
برخی از کاربردهای تصاویر ماهواره ای به شناسایی عوارض معطوف میشوند و در آنها نیازی به دانستن ارزش واقعی هر پیکسل نمیباشد. برای مثال هنگامی که میخواهید عوارضی را که بر روی یک تصویر ماهواره ای رقومی دیده میشود ترسیم نمایید، ارزش مقدار هر پیکسل کمک چندانی به شما نمیکند و مهم این است که بتوانید عوارض را از یکدیگر متمایز سازید. در اینحالت بهبود کنتراست تصاویر بسیار حائز اهمیت میگردد.
اما در برخی موارد ارزش مقدار ذخیره شده برای هر پیکسل از اهمیت بالایی برخوردار است. برای مثال هنگامی که میخواهید شاخص NDVI را برای یک تصویر ماهواره ای چند بانده محاسبه کنید، مقادیر ذخیره شده در تک تک پیکسلها اهمیت پیدا میکنند.
در مواردی که ارزش اولیه پیکسلها برای شما ارزش چندانی ندارد، میتوانید با تغییر کنتراست تصاویر، قدرت تفکیک بالاتری را ایجاد کنید. این قدرت تفکیک بالاتر به شما کمک میکند تا بتوانید حدود هر عارضه بر روی تصویر را تشخیص داده و عوارض را از یکدیگر متمایز نمایید. اما این کار چگونه امکان پذیر است؟
همانطور که میدانید ارزش ثبت شده برای هر پیکسل در یک باند از تصویر ماهواره ای، بین اعداد صفر و 255 متغیر است. هرچه به سمت صفر میرویم تصویر تیره تر شده و هر چه به سمت 255 حرکت میکنیم پیکسل ما روشن تر دیده میشود. در تصاویری که کنتراست پایین تری دارند، بیشتر پیکسلها دارای مقادیری از ارزش هستند که محدوده کوچکی را به خود اختصاص داده است. مثلاً اکثر پیکسلها مقادیری بین 50 تا 100 دارند. در اینحالت بخشهایی از محدوده 250 واحدی ما خالی میماند و عوارض اختلاف رنگ کمتری خواهند داشت.

همانطور که در تصویر بالا مشاهده میکنید، کنتراست پایین تصویر در سه باند RGB باعث شده است تا بخشهای موجود در تصویر به سختی از یکدیگر متمایز شوند. همچنین اگر به نمودار هیستوگرام هر باند دقت کنیم متوجه خواهیم شد که در هر باند، بخش کوچکی از فضای موجود برای نمایش هر رنگ استفاده شده است.
برای بهبود کنتراست تصاویر به روشهای مختلفی میتوانیم فضای موجود بین ارزش صفر تا 255 را بین پیکسلها تقسیم نماییم. مثلاً فرض میکنیم در یکی از باندهای تصویر ما مینیمم و ماکزیمم ارزشها 50 و 100 باشد. اگر بخواهیم مینیمم را بر روی صفر قرار داده و ماکزیمم بر روی 250 قرار گیرد، درواقع تصویری ایجاد کرده ایم که در آن فاصله بین ارزش پیکسلها 5 برابر شده است. در اینحالت اگر بین دو پیکسل یک واحد اختلاف ارزش وجود داشته باشد، این یک واحد اختلاف به 5 واحد افزایش خواهد یافت. مسلماً تمایز بین دو پیکسل با ارزشهای متوالی بسیار سخت تر از تمایز بین دو پیکسلی خواهد بود که 5 واحد با یکدیگر اختلاف دارند. این اختلاف در کل تصویر تسری پیدا نموده و درنهایت باعث افزایش قدرت تمایز عوارض خواهد شد.

تصویری که در بالا مشاهده میکنید همان تصویر قبل است که با استفاده از روشی که خدمتتان عرض شد افزایش کنتراست پیدا کرده است. به دامنه ارزش پیکسلها در هر باند دقت کنید. به کار گیری دامنه وسیعتر برای نشان دادن ارزش پیکسلها باعث افزایش وضوح تصویر شده است.
درحقیقت نوعی کلاسه بندی یا همان Classification برای مقادیر ارزش پیکسلها در نظر گرفته شده است و کلیه مقادیر در کلاسهایی که از صفر شروع شده و به 255 ختم میشوند افراز شده اند. روشهای مختلفی برای نحوه کلاسه بندی ارزشها وجود دارد که برخی از آنها مبتنی بر محاسبه پارامترهای آماری هستند. روشهای مختلفی چون Minimum-Maximum ، Standard Deviations ، Histogram Specification ، Histogram Equalize و Percent Clip نمونه هایی از روشهای کلاسه بندی هستند که در نرم افزار ArcGIS برای بهبود کنتراست تصاویر در نظر گرفته شده اند.
کافیست تا یک نمونه از فایل رستری را در نرم افزار ArcGIS باز کرده و در پنجره Layer Properties و در سربرگ Symbology ، حالت نمایش را در حالت Stretched قرار دهید و سپس در بخش Stretch گزینه Type را تغییر دهید تا اثر تغییر روش کلاسه بندی را در نمایش فایل رستری خود مشاهده نمایید.
منبع
افزایش کنتراست یک تصویر با دستور histeq در متلب
دستور histeq در متلب، برای افزایش کنتراست یک تصویر به کار می رود. چنانچه مقادیر مربوط به رنگ های به کار رفته در یک تصویر را مشاهده کنیم (این کار با دستور imhist در متلب، امکان پذیر می باشد)، آنگاه ممکن است که بخشی از رنگ ها، به مقدار زیاد، در تصویر به کار رفته باشند و بخشی دیگر، کمتر در تصویر باشند. افزایش کنتراست، باعث می شود که میزان به کار رفتن رنگ های مختلف، به هم نزدیکتر شود و دیگر تفاوت زیادی که ذکر شد، وجود نداشته باشد. به مثال زیر توجه کنید :
مثال
clear all close all clc img=imread(‘image.jpg’); img=rgb2gray(img); imshow(img); figure histeq(img);
نتیجه
تصویر اصلی :

تصویر پس از افزایش کنتراست :

افزایش کنتراست با Contrast stretching
همانطوری که می بینید پراکندگی پیکسل ها در بازه مشخصی هستش و شما در تصویر نه سیاه و نه سفید مطلق دارید با نرمالیز کردن می تونید طوری توزیع را مقدار پیکسل ها را تغییر بدید که کل بازه ۰ تا ۲۵۵ را پوشش بده که هیستوگرام و تصویر بعد از نرمالیزمیشه به صورت زیر:
یک نکته ای را که باید متذکر بشم تفاوت Normalize با histogram equalization هستش عملیات نرمالیز به صورت خطی داده ها را تغییر مقیاس میده ولی عملیات histogram equalization به صورت غیر خطی هستش.
فرمول برای نرمالیز کردن
تصویر فعلی که قرار نرمالیز بشه دارای یک Max و Min هستش و شما قصد دارید تصویر را به بازه جدید تغییر مقیاس دهید یعنی یک بازه با حد پایین NewMin و حد بالای NewMax که ما توی تصویر معمولاً از بازه 0 و 255 استفاده می کنیم. حال باید dynamic range تصویر اصلی و تصویر نهایی را به صورت زیر محاسبه کنید.
dr_src = Max – Min
dr_dst = NewMax – NewMin
پس از آن مقدار scale را محاسبه می کنیم.
scale = dr_dst/dr_src
I_n = (I – Min) * scale + NewMin
یکی دیگه از کاربردهای آماری دیگه ای که داره گاهی اوقات شما آرایه ای از مقادیر دارید و بازه اعداد ممکنه متفاوت باشند در این شرایط شما می تونید از نرمالیز استفاده کرده و داده را به بازه دلخواه تغییر مقیاس بدید مثال خیلی کاربردیش زمانیکه شما قصد دارید یک شبکه عصبی MLP را آموزش بدید و در شرایطی که active function شما از نوع سیگموید باشه برای همگرایی سریع شبکه باید داده های ورودی شبکه در بازه منفی یک و یک باشه که شما به راحتی می تونید با نرمالیز کردن داده های ورودی به شکل مطلوب تغییرشون بدید.
منبع
افزایش کنتراست با تعدیل هیستوگرام
برای تعدیل هیستوگرام :
مرحله۱ – PMF ( تابع جرم احتمال ) رو حساب می کنیم .
وقتی هیستوگرام را محاسبه می کنیم میزان فراوانی یا فرکانس هر سطح خاکستری نمایش داده میشود مانند شکل زیر:

PMF در ابتدا مجموع فراوانی ها را محاسبه می کند و سپس مقدار هر فراوانی را بر کل فراوانی ها تقسیم می کنیم.

pmf تابعی است که احتمال وقوع متغیر تصادفی x=k را نشان میدهد.( دقت داشته باشید که در pmf مقادیر k گسسته هستند) و به این دلیل که این تابع احتمال را نشان می دهدبنانبراین می بایست دو شرط زیر هم برای این تابع برقرار باشند :
1_ (p(x باید بزرگتر مساوی 0 باشد .
2_ به ازای همه k ها مجموع تمام (p(x=k ها باید 1 شود .
برای هیستوگرام عکس هم میشه تابعی با شرایط بالا پیدا کرد :
اگر x را به صورت یک متغیر تصادفی داخل فضای نمونه شامل همه رنگ ها در نظر بگیریم و k هم مجموعه اعداد 0 تا 255 باشد، pmf را می توان با تقسیم تعداد پیکسل ها با رنگ مورد نظر بر تعداد کل پیکسل ها محاسبه کرد :
p(x=k)=number of pixels with color k / total number of pixels
کد ++C این کار به صورت زیر است :
#include "stdafx.h"
#include < vector >
#include < string >
#include < iostream >
#include < algorithm >
#include < numeric >
using namespace std;
void computePMF(const vector < int > &src,vector < float > &dst){
float sum = (float)std::accumulate(src.begin(), src.end(), 0);
dst.resize(src.size());
for (size_t i=0; i < src.size();i++)
dst[i] = src[i] / sum;
}
int _tmain(int argc, _TCHAR* argv[])
{
vector < int > hist(10);
for (auto &item : hist)
item = rand()%5;
vector < float > pmf;
computePMF(hist,pmf);
for (auto item :pmf)
cout < < item < < endl;
return 0;
}
مرحله ۲ – با استفاده از PMF مقادیر CDF ( تابع توزیع تجمعی) را حساب می کنیم .
توزیع تجمعی یعنی وقتی PMF را محاسبه کردید بعد از آن مقدار هر اندیس در CDF برابر است با مقدار مجموع همه PMF های کوچکتر و مساوی با آن اندیس می باشد.
اگر PMF به صورت زیر باشد:

CDF به صورت زیر خواهد شد.

کد ++C محاسبه CDF به صورت زیر می باشد:
#include "stdafx.h"
#include < vector >
#include < string >
#include < iostream >
#include < algorithm >
#include < numeric >
using namespace std;
void computePMF(const vector < int > &src,vector < float > &dst){
float sum = (float)std::accumulate(src.begin(), src.end(), 0);
dst.resize(src.size());
for (size_t i=0; i < src.size();i++)
dst[i] = src[i] / sum;
}
void computeCDF(const vector < float > pmf,vector<float> &cdf){
cdf.resize(pmf.size());
float sum=0;
for (size_t i=0; i < pmf.size();i++){
cdf[i] = sum + pmf[i];
sum += pmf[i];
}
}
int _tmain(int argc, _TCHAR* argv[])
{
vector < int > hist(10);
for (auto &item : hist)
item = rand()%5;
vector < float > pmf;
computePMF(hist,pmf);
vector < float > cdf;
computeCDF(pmf,cdf);
for (auto item :cdf)
cout < < item < < endl;
return 0;
}
مرحله ۳ – نهایتا مقادیر CDF بدست آمده رو normalize می کنیم
که مقادیر ScaledCDF رنگ خروجی ما هستن
برای equalize کردن Histogram عکس رنگی بوسیله opencv
اول عکس رو به فضای رنگی YCrCb میبریم
بعد بر روی کانال مربوط به شدت نور بوسیله تابع equalizeHist عملیات مربوطه رو انجام میدیم
کد :
#include < opencv2/highgui/highgui.hpp >
#include < opencv2/imgproc/imgproc.hpp >
#include < iostream >
using namespace cv;
int main( )
{
const char* original_window="Source";
const char* equalized_window="Equalized image";
Mat image = imread("F:\\image1.jpg");
Mat equalized_image;
std::vector < Mat > channels;
cvtColor(image, equalized_image, CV_BGR2YCrCb);
split(equalized_image,channels);
equalizeHist(channels[0], channels[0]);
merge(channels,equalized_image);
cvtColor(equalized_image, equalized_image, CV_YCrCb2BGR);
namedWindow(original_window,WINDOW_NORMAL);
namedWindow(equalized_window,WINDOW_NORMAL);
imshow(original_window,image);
imshow(equalized_window,equalized_image);
waitKey(0);
}

این کد هم به زبان ++C است که به راحتی قابل تبدیل به #C می باشد:
#include < iostream >
#include < opencv2/highgui/highgui.hpp >
#include < opencv2/imgproc/imgproc.hpp >
using std::cout;
using std::cin;
using std::endl;
using namespace cv;
void imhist(Mat image, int histogram[])
{
// initialize all intensity values to 0
for(int i = 0; i < 256; i++)
{
histogram[i] = 0;
}
// calculate the no of pixels for each intensity values
for(int y = 0; y < image.rows; y++)
for(int x = 0; x < image.cols; x++)
histogram[(int)image.at < uchar > (y,x)]++;
}
void cumhist(int histogram[], int cumhistogram[])
{
cumhistogram[0] = histogram[0];
for(int i = 1; i < 256; i++)
{
cumhistogram[i] = histogram[i] + cumhistogram[i-1];
}
}
void histDisplay(int histogram[], const char* name)
{
int hist[256];
for(int i = 0; i < 256; i++)
{
hist[i]=histogram[i];
}
// draw the histograms
int hist_w = 512; int hist_h = 400;
int bin_w = cvRound((double) hist_w/256);
Mat histImage(hist_h, hist_w, CV_8UC1, Scalar(255, 255, 255));
// find the maximum intensity element from histogram
int max = hist[0];
for(int i = 1; i < 256; i++){
if(max < hist[i]){
max = hist[i];
}
}
// normalize the histogram between 0 and histImage.rows
for(int i = 0; i < 256; i++){
hist[i] = ((double)hist[i]/max)*histImage.rows;
}
// draw the intensity line for histogram
for(int i = 0; i < 256; i++)
{
line(histImage, Point(bin_w*(i), hist_h),
Point(bin_w*(i), hist_h - hist[i]),
Scalar(0,0,0), 1, 8, 0);
}
// display histogram
namedWindow(name, CV_WINDOW_AUTOSIZE);
imshow(name, histImage);
}
int main()
{
// Load the image
Mat image = imread("scene.jpg", CV_LOAD_IMAGE_GRAYSCALE);
// Generate the histogram
int histogram[256];
imhist(image, histogram);
// Caluculate the size of image
int size = image.rows * image.cols;
float alpha = 255.0/size;
// Calculate the probability of each intensity
float PrRk[256];
for(int i = 0; i < 256; i++)
{
PrRk[i] = (double)histogram[i] / size;
}
// Generate cumulative frequency histogram
int cumhistogram[256];
cumhist(histogram,cumhistogram );
// Scale the histogram
int Sk[256];
for(int i = 0; i < 256; i++)
{
Sk[i] = cvRound((double)cumhistogram[i] * alpha);
}
// Generate the equlized histogram
float PsSk[256];
for(int i = 0; i < 256; i++)
{
PsSk[i] = 0;
}
for(int i = 0; i < 256; i++)
{
PsSk[Sk[i]] += PrRk[i];
}
int final[256];
for(int i = 0; i < 256; i++)
final[i] = cvRound(PsSk[i]*255);
// Generate the equlized image
Mat new_image = image.clone();
for(int y = 0; y < image.rows; y++)
for(int x = 0; x < image.cols; x++)
new_image.at < uchar > (y,x) = saturate_cast < uchar > (Sk[image.at < uchar > (y,x)]);
// Display the original Image
namedWindow("Original Image");
imshow("Original Image", image);
// Display the original Histogram
histDisplay(histogram, "Original Histogram");
// Display equilized image
namedWindow("Equilized Image");
imshow("Equilized Image",new_image);
// Display the equilzed histogram
histDisplay(final, "Equilized Histogram");
waitKey();
return 0;
}
منبع
تلفن های تماس:
تلفن: ۹۱۰۰۱۸۸۱(۰۳۱)
بازرگانی و فروش:۰۹۱۳۶۵۳۱۸۸۱
پشتیبانی: ۰۹۱۱۷۶۱۰۲۷۵
ساعات کاری
از شنبه تا چهارشنبه : ۰۹:۰۰ تا ۱۷:۰۰
پنچ شنبه ها : از ۰۹:۰۰ تا ۱۳:۳۰


![{\displaystyle \delta _{t+1}(j)=b_{j}(o_{t+1})[max\delta _{t}(i)a_{ij}],\qquad 1\leq i\leq N,\qquad 1\leq t\leq T-1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/341a45475d2d12accb08d82f405386c59e4075f8)




![{\displaystyle \ Q(\lambda ,{\bar {\lambda }})=\sum _{q}p\{q|O,\lambda \}log[p\{O,q,{\bar {\lambda }}\}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a669bd0b99c6cb8b0638b6cea62136faf6886442)




![{\displaystyle \gamma _{t}(i)=\left[{\frac {\alpha _{t}(i)\beta _{t}(i)}{\sum _{i=1}^{N}\alpha _{t}(i)\beta _{t}(i)}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/208320604d962f63ab6c3b1f4c30f35fafd0371c)





![{\displaystyle \ \Theta ^{new}=\Theta ^{old}-\eta \left[{\frac {\partial j}{\partial \Theta }}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b0046e064301e13c53db6ae1b74307db96cadd2)






![{\displaystyle \ L_{tot}^{free}=\sum _{m=1}^{N}L_{m}^{I}=\sum _{m=1}^{N}[\sum _{i\in \lambda _{m}}\alpha _{t}(i)\mathrm {B} _{t}(i)]\sum _{m=1}^{N}\sum _{i\in \lambda _{i}}\alpha _{T}(i)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/48e2d5288de6f92113a9fd886bb4cb6d940ecb4e)





































