مدل مخفی مارکوف (Hidden Markov Model) قسمت 1
مدل مخفی مارکوف (به انگلیسی: Hidden Markov Model) یک مدل مارکوف آماری است که در آن سیستم مدل شده به صورت یک فرایند مارکوف با حالتهای مشاهده نشده (پنهان) فرض میشود. یک مدل پنهان مارکوف میتواند به عنوان سادهترین شبکه بیزی پویا در نظر گرفته شود.
در مدل عادی مارکوف، حالت بهطور مستقیم توسط ناظر قابل مشاهده است و بنابراین احتمالهای انتقال بین حالتها تنها پارامترهای موجود است. در یک مدل مخفی مارکوف، حالت بهطور مستقیم قابل مشاهده نیست، اما خروجی، بسته به حالت، قابل مشاهده است. هر حالت یک توزیع احتمال روی سمبلهای خروجی ممکن دارد؛ بنابراین دنبالهٔ سمبلهای تولید شده توسط یک مدل مخفی مارکوف اطلاعاتی دربارهٔ دنبالهٔ حالتها میدهد. توجه داشته باشید که صفت ‘پنهان’ به دنبالهٔ حالتهایی که مدل از آنها عبور میکند اشاره دارد، نه به پارامترهای مدل؛ حتی اگر پارامترهای مدل بهطور دقیق مشخص باشند، مدل همچنان ‘پنهان’ است.
مدلهای مخفی مارکوف بیشتر بهدلیل کاربردشان در بازشناخت الگو، مانند تشخیص صدا و دستخط، تشخیص اشاره و حرکت، برچسبگذاری اجزای سخن، بیوانفورماتیک و … شناختهشده هستند.

مثالی از پارامترهای احتمالاتی یک مدل مخفی مارکوف
x — حالتها
y — مشاهدههای ممکن
a — احتمالهای انتقال بین حالتها
b — احتمالهای خروجیها
شرح ازنظر مسائل ظرفها
مدل مخفی مارکوف در حالت گسسته جز خانوادهٔ مسائل ظرفها قرار میگیرد. بهطور مثال از ربینر ۱۹۸۹: ظروف x1،x2،x3… و توپهای رنگی y1,y2,y3… را در نظر میگیریم، که نفر مقابل دنبالهای از توپها را مشاهده کرده ولی اطلاعی از دنبالهٔ ظرفهایی که توپها از آنها انتخابشده ندارد. ظرف n ام با احتمالی وابسته به ظرف n-1 ام انتخاب میشود و چون به انتخاب ظرفهای خیلی قبلتر وابسته نیست یک فرایند مارکوف است.
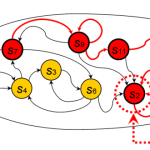
معماری مدل مخفی مارکوف
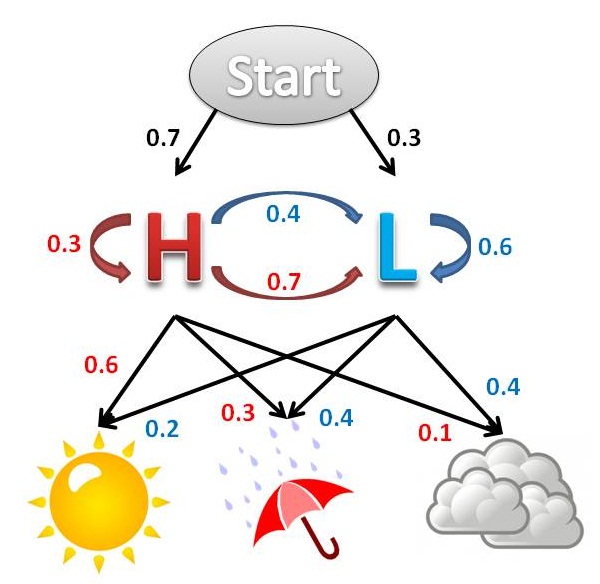
شکل زیر معماری کلی یک نمونه HMM را نشان میدهد. هر شکل بیضی یک متغیر تصادفی است که میتواند هر عددی از مقادیر را انتخاب کند. متغیر تصادفی یک حالت پنهان در زمان t و متغیر تصادفی مشاهده در زمان است. فلشها به معنای وابستگیهای شرطی میباشند. از شکل مشخص است که توزیع احتمال شرطی متغیر پنهان ، در همهٔ زمان هایt مقداری را برای x ارائه میدهد که فقط به مقدار متغیر پنهان وابسته است: مقادیر در زمانهای t-2 و قبلتر از آن هیچ اثری ندارند. این مشخصهٔ مارکف نامیده میشود. بهطور مشابه، مقدار متغیر مشاهدهای تنها به مقدار متغیر پنهان (هر دو در زمان خاص t) بستگی دارد. در حالت استاندارد مدل مخفی مارکوف که در اینجا در نظر گرفته شدهاست، فضای حالت متغیرهای پنهان گسسته است؛ درحالیکه متغیرهای مشاهدهای میتوانند گسسته یا پیوسته (از توزیع گوسین) باشند.
در مدل مخفی مارکوف دو نوع پارامتر وجود دارد:احتمال جابهجاییها (بین حالات) و احتمال خروجیها (یا مشاهدات). احتمال جابهجایی نحوهٔ انتقال از حالت t-1 به t را کنترل میکند.
فضای حالت پنهان شامل N مقدار ممکن برای حالات است. متغیر پنهان در زمان t میتواند هر یک از این مقادیر را اختیار کند. احتمال جابجایی احتمال این است که در زمان t در حالت k (یکی از حالات ممکن) و در زمان t+1 در حالت k1 باشیم. بنابرین در کل احتمال جابجایی وجود دارد. (مجموع احتمالات جابجایی از یک حالت به تمام حالتهای دیگر ۱ است)
احتمال خروجی، احتمال رخ دادن هر یک از اعضای مجموعهٔ مشاهدهای را برای هر حالت پنهان ممکنه مشخص میسازد که میتواند از یک توزیع احتمال پیروی کند. تعداد اعضای مجموعهٔ مشاهدهای بستگی به طبیعت متغیر مشاهدهای دارد.
اگر تعداد اعضای مجموعهٔ متغیرهای مشاهدهای برابر M باشد، بنابراین مجموع تعداد احتمالات خروجی NM میباشد/

مسایلی که به کمک مدل مخفی مارکوف حل میشود
با توجه به پارامترهای مدل مخفی مارکوف، میتوانیم مسایلی به صورت زیر را حل کنیم.
- Annotation: مدل را داریم به این معنی که احتمالات مربوط به انتقال از حالتی به حالت دیگر و همینطور احتمال تولید الفبا در هر حالت معلوم است. توالی از مشاهدات داده شده، میخواهیم محتملترین مسیری (توالی حالات) که توالی را تولید میکند را پیدا کنیم. الگوریتم viterbi میتواند اینگونه مسایل را به صورت پویا (Dynamic) حل کند.
- classification: مدل را داریم، توالی از مشاهدات داده شدهاست، میخواهیم احتمال (کل) تولید شدن این توالی توسط این مدل را (جمع احتمالات تمامی مسیرهایی که این توالی را تولید میکنند) حساب کنیم. الگوریتم forward
- Consensus: مدل را داریم، میخواهیم بدانیم محتملترین توالی که توسط این مدل تولید میشود (توالی که بیشترین احتمال را داراست) چیست. الگوریتم Backward
- Training: ساختار مدل را داریم به این معنی که تعداد حالات و الفبای تولیدی در هر حالت معلوم است، تعدادی توالی داریم (دادههای آموزش) میخواهیم احتمال انتقال بین حالات و همینطور احتمال تولید الفبا در هر حالت را محاسبه کنیم. الگوریتم Baum-Welch
یادگیری
وظیفه یادگیری در HMM، یافتن بهترین احتمالات جابجاییها و خروجیها بر اساس یک دنباله یا دنبالههایی از خروجی هاست. معمولاً این پارامترها به وسیله متد maximum likelihood بر اساس خروجی داده شده تخمین زده میشوند. هیچ الگوریتم قطعی برای حل این مسئله وجود ندارد ولی برای پیدا کردن maximum likelihood محلی میتوان از الگوریتمهای کارایی مانند Baum-welch algorithmو یا Baldi-chauvin algorithmاستفاده کرد. الگوریتم Baum-Welch نمونهای از الگوریتم forward-backwardو به صورت خاص موردی از الگوریتم exception-maximization میباشد.
یک مثال ملموس
دو دوست به نامهای آلیس و باب را در نظر بگیرید. آنها دور از هم زندگی کرده و هر روز دربارهٔ کارهای روزمرهشان با هم تلفنی صحبت میکنند. فعالیتهای باب شامل “قدم زدن در پارک”،”خرید کردن” و “تمیز کردن آپارتمان” میشود. انتخاب اینکه هر روز کدام کار را انجام دهد منحصراً بستگی به هوای همان روز دارد. آلیس اطلاع دقیقی از هوای محل زندگی باب نداشته ولی از تمایلات کلی وی آگاه است (بنا به نوع هوا چه کاری را دوست دارد انجام دهد). بر اساس گفتههای باب در پایان هر روز، آلیس سعی میکند هوای آن روز را حدس بزند. آلیس هوا را یک زنجیرهٔ گسستهٔ مارکوف میپندارد که دو حالت “بارانی” و “آفتابی” دارد. اما بهطور مستقیم هوا را مشاهده نمیکند؛ بنابراین، حالات هوا بر او پنهان است. در هر روز احتمال اینکه باب به “قدم زدن”،”خرید کردن” و “تمیز کردن”بپردازد بستگی به هوا داشته و دارای یک احتمال مشخص است. مشاهدات مسئله شرح فعالیتهایی است که باب در انتهای هر روز به آلیس میگوید.
آلیس اطلاعات کلی دربارهٔ هوای محل زندگی باب و اینکه در هر نوع آب و هوا با چه احتمالی چه کار انجام میدهد را دارد. به عبارت دیگر پارامترهای مسئله HMM معلوم هستند که در کد زیر مشاهده میشوند:
states = ('Rainy', 'Sunny')
observations = ('walk', 'shop', 'clean')
start_probability = {'Rainy': 0.6, 'Sunny': 0.4}
transition_probability = {
'Rainy': {'Rainy': 0.7, 'Sunny': 0.3},
'Sunny': {'Rainy': 0.4, 'Sunny': 0.6},
}
emission_probability = {
'Rainy': {'walk': 0.1, 'shop': 0.4, 'clean': 0.5},
'Sunny': {'walk': 0.6, 'shop': 0.3, 'clean': 0.1},
}
در این کد start_probability نمایانگر احتمال رخ دادن هر یک از حالات HMM (بارانی یا آفتابی) در روز اولی که باب با آلیس صحبت میکند میباشد.transition_probability نمایانگر تغییر هوا بر اساس قواعد زنجیرهٔ مارکو است. بهطور مثال اگر امروز بارانی باشد به احتمال ۳۰٪فردا آفتابی است.emition_probability نمایانگر این است که باب علاقه دارد که در هر هوایی چه کار کند بهطور مثال در هوای بارانی با احتمال ۵۰٪ آپارتمانش را تمیز کرده یا در هوای آفتابی با احتمال ۶۰٪در پارک قدم میزند.

مدل مخفی مارکوف (Hidden Markov Model) قسمت 1
مدل مخفی مارکوف (Hidden Markov Model) قسمت 2






دیدگاه خود را ثبت کنید
تمایل دارید در گفتگوها شرکت کنید؟در گفتگو ها شرکت کنید.