بایگانی برچسب برای: lkxr thcd

سیستم استنتاج فازی چیست؟ قسمت 1

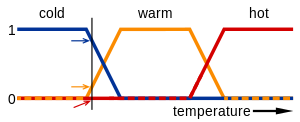
مقدمه

جهان واقعی پيچيده است و این پيچيدگی به طور كلی از عدم قطعيت آن ناشی می شود، انسان به خاطر داشتن قدرت تفکر قادر به درک ابهامات و پيچيدگی هاست. بسياری از مشکلات دنيای واقعی با نظریه مجموعه های كلاسيک قابل حل نيستند، در تئوری مجموعه كلاسيک یک عنصر یا عضو مجموعه است یا نيست یا صفر است یا یک. نقطه مقابل تئوری مجموعه كلاسيک تئوری فازی قرار دارد.

تئوری مجموعه فازی ابزاری قوی جهت مواجه با عدم قطعيت ناشی از ابهام است، اگرچه سيستم های فازی پدیده های غيرقطعی و نامشخص را توصيف می كنند با این حال خود تئوری فازی یک تئوری دقيق است.

آشنایی با سيستم استنتاج فازی، مزایا و معایب آن ها می تواند در طراحی سيستم های خبره فازی و خروجی تخمين زده شده توسط سيستم موثر باشد، در این نوشته پس از تعریف سيستم استنتاج فازی، الگوریتم های استنتاج ممدانی، سوگنو مقایسه و بررسی می شوند. با ما همراه باشید.

منطق فازی

منطق فازی اولين بار توسط آقای پروفسور لطفی زاده در رساله ای به نام «مجموعه های فازی – اطلاعات و كنترل» در سال 1965 معرفی گردید و در دهه 1970 رشد و كاربرد عملی پيدا كرد، بزرگترین رخدادهای این دهه توليد كنترل كننده های فازی برای سيستم های واقعی بود.

منطق فازی از كاربردهای موفق در درزمينه ی مجموعه های فازی است كه در آن متغيرها زبانی هستند نه عددی، منطق فازی در برابر منطق باینری یا ارسطویی قرار دارد كه همه چيز را فقط به دو صورت بله یا خير، سياه و سفيد، صفر و یک می بيند، این منطق در بازه بين صفر و یک تغيير می كند.

مزایا و معایب منطق فازی

از جمله مزایای منطق فازی می توان به موارد زیر اشاره نمود:

  • منطق فازی به تفکر و منطق انسان نزدیک است.
  • برنامه های طراحی شده با منطق فازی سریع و كم هزینه هستند.
  • به راحتی می تواند مدلسازی شوند.
  • به طور گسترده ای در سيستم های كنترل و پيش بينی تصميم قابل استفاده است.
  • برای توصيف پدیده های غيرقطعی و نامشخص به كار می روند.

از جمله معایب منطق فازی می توان به موارد زیر اشاره كرد:

  • قوانين منطق فازی توسط تجربه متخصص تعيين می شوند.
  • تجزیه و تحليل یک سيستم با منطق فازی دشوار است یعنی نمی توان قبل از واكنش آن را تخمين زد.
  • توابع توسط آزمون و خطا مشخص می شوند كه زمان بر هستند.

سيستم های استنتاج فازی

در شکل 1 معماری سيستم استنتاج فازی نشان داده شده است. همانطور كه مشخص است سيستم استنتاج فازی به طور كلی از اجزاء زیر ساخته شده است:

  1. فازی ساز
  2. موتور استنتاج فازی
  3. دفازی ساز

روند تبدیل متغيرهای صریح به متغيرهای زبانی را فازی سازی می گویند. موتور استنتاج با استفاده از الگوریتم های استنتاج، قوانين را ارزیابی و استنتاج می كند و پس از تجميع قوانين خروجی توسط واحد دفازی ساز به مقدار صریح یا عددی تبدیل می شود.

انواع روش های دفازی سازی شامل مركز ثقل ناحيه (COA)، نيمساز ناحيه (BOA )، كوچکترین ماكزیمم (SOM)، بيشترین ماكزیمم (LOM )، ميانگين ماكزیمم (MOM)، ميانگين وزنی (WA)، مجموع وزنی (WS) می باشد كه به طور كلی COA و WA بيشترین كاربردها را دارد.

سیستم استنتاج فازی

کاربردهای سيستم استنتاج فازی

استفاده از سيستم های فازی روز به روز گسترش یافت و كاربرد آن درزمينه های مختلفی مانند سيستمهای خبره فازی، سيستم های پشتيبانی تصميم، برآورد هزینه احتمالی پروژه با استفاده از تجزیه و تحليل ریسک، سيستمهای كنترل، پردازش تصویر، ارتباطات، بازرگانی، پزشکی، نظامی و آموزشی، رباتها، سيستم قدرت و رآكتور هسته ای و مهندسی خودرو به كار گرفته شد.

یکی از اولين محصولاتی كه از سيستم های فازی استفاده نمودند ماشين لباسشویی بود كه توسط شركت ماتسو شيتا در سال 1990 در ژاپن عرضه شد، در این ماشين لباسشویی از سيستم فازی برای تنظيم خودكار تعداد دورهای مناسب، بر اساس نوع، ميزان كثيفی و حجم لباس استفاده شد. سيستم كنترل فازی متروی سندایی نيز از دیگر كاربردهای سيستم فازی است كه چهار پارامتر، ایمنی، راحتی سرنشينان، رسيدن به سرعت مطلوب و دقت ترمز را به طور همزمان در نظر می گيرد. امروزه از سيستم فازی نيز در تثبيت كننده تصویر دیجيتال در دوربين ها و در بخش هایی نظير موتور، انتقال نيرو و ترمز در اتومبيل ها، تغييرات دنده خودكار و تصفيه آب استفاده شده است .

انواع الگوریتم های استنتاج فازی

1-الگوریتم استنتاج ممدانی

سيستم استنتاج ممدانی را ممدانی و اسيليان در سال 1975 پيشنهاد دادند. این سيستم ها به دليل داشتن طبيعت بصری و تفسيری از قوانين می توانند به طور گسترده ای در سيستم های پشتيبانی تصميم استفاده شوند، همچنين دارای قدرت بيانی بالایی هستند و می توانند به هر دو صورت چند ورودی و چند خروجی (MIMO) و چند ورودی و یک خروجی(MISO) پياده سازی می شود.

دیاگرام كلی سيستم استنتاج فازی ممدانی در شکل 2 نشان داده شده است، سيستم استنتاج ممدانی از مجموعه های فازی به عنوان نتيجه قانون استفاده می كند و خروجی هر قانون به صورت غيرخطی و فازی است. همچنين از لحاظ روش دفازی سازی با بقيه سيستم های استنتاج متفاوت است. روش های دفازی سازی در سيستم استنتاج ممدانی به صورت BOA، COA، SOM, ،LOM, ،MOM هستند.

دیاگرام سیستم استنتاج فازی ممدانی

فرم كلی قوانين در سيستم ممدانی در شکل 3 نشان داده شده است، نتایج هر قانون كه با مقدارهای c1 و c2 مشخص می باشند، همانطور كه مشخص است پس ازتجميع نتایج حاصل از قوانين، عمل دفازی سازی بر روی تابع عضویت خروجی z انجام می گيرد و نتایج به صورت عددی به دست می آید.

اجرای قوانین در سیستم استنتاج فازی ممدانی
شکل 3 :فرم كلی اجرای قوانين در سيستم استنتاج ممدانی

2- الگوریتم استنتاج تاکاگی سوگنو

سيستم استنتاج تاكاگی سوگنو، توسط تاكاگی و ميشيو سوگنو در سال 1985 به منظور توسعه یک رویکرد سيستماتيک برای توليد قوانين فازی ارائه شد، این سيستم استنتاج بيشتر در سيستم های كنترلی و در زمينه هایی كه نياز به محاسبات ریاضی باشد مورداستفاده قرار می گيرد. شکل 4 دیاگرام یک سيستم استنتاج سوگنو را نشان می دهد. خروجی الگوریتم استنتاج سوگنو از یک چند جمل های مرتبه اول از متغيرهای ورودی به عنوان نتيجه قانون استفاده می كند و روش دفازی سازی در آن از نوع روشهای دفازی سازی WS,WA می باشد، همچنين سيستم استنتاج سوگنو به صورت MISO پياده سازی می شود و نمی تواند به صورت MIMO پياده سازی شود.

دیاگرام یک سیستم استنتاج سوگنو

شمای كلی ارزیابی قوانين با استفاده از روش سوگنو در شکل 1 نشان داده شده است. همانطور كه مشخص است نتایج قانون در سيستم استنتاج سوگنو به صورت صریح و خطی می باشد.

نمای کلی از اجرای قوانین در سیستم استنتاج سوگنو

مقایسه الگوریتم استنتاج فازی ممدانی و سوگنو

در جدول (1) مقایسه ای بين الگوریتم های استنتاج ممدانی و سوگنو نشان داده شده است. الگوریتم استنتاج سوگنو بيشتر در سيستم های كنترلی و سيستم هایی كه احتياج به محاسبات ریاضی دارند استفاده می شود اما در الگوریتم استنتاج ممدانی نتایج منطقی با یک ساختار نسبتاً ساده بيان می شود و بيشتر در سيستم های پشتيبانی تصميم و سيستم هایی كه قابليت تفسيری از قوانين را دارند استفاده می شوند، خروجی الگوریتم استنتاج ممدانی غيرخطی و فازی است اما خروجی سيستم استنتاج سوگنو خطی است، الگوریتم ممدانی در بسياری از عملکردها كه دقت خروجی و انعطاف پذیری مهم است به خوبی عمل نمی كند ولی موتور استنتاج تاكاگی سوگنو انعطاف پذیرتر و از دقت عملکرد بالاتری برخوردار می باشد و از لحاظ محاسباتی نسبت به ممدانی مؤثرتر است، زیرا فرایند دفازی سازی به زمان محاسباتی كمتری نياز دارد، اما فقط برای تجزیه وتحليل سيستم های كنترلی MISO خطی بهتر عمل می كند.

مقایسه بین الگوریتم های استنتاج فازی ممدانی و سوگنو

نتيجه گيری

امروزه كاربردهای فازی در طراحی های مختلف سيستم های غيرقطعی، نشان دهنده عملکرد بالا و رشد سریع این سيستم ها است، هرچند كه علمکرد الگوریتم های استنتاج فازی مشابه هم هستند اما رعایت تفاوت های آنها در طراحی سيستم های فازی می تواند در خروجی سيستم مؤثر باشد، الگوریتم استنتاج سوگنو به خاطر داشتن دقت و انعطاف پذیری بالا درطراحی سيستم های حساس و كنترلی استفاده می شود ولی سيستم های ممدانی به خاطر خاصيت تفسيری و خروجی فازی كه از قوانين دارند بيشتر در زمينه سيستم های انسانی استفاده می شوند.

منبع : مقاله مروری بر الگوریتم های استنتاج فازی نویسندگان: عالمه جعفری سوق، حامد شهبازی

مروری بر الگوریتم های استنتاج فازیدریافت

هم چنین برای دریافت اطلاعات بیشتر می توانید فایل آموزشی سیستم های استنتاج فازی تهیه شده توسط دکتر اکبری را از لینک زیر دریافت نمایید.

Fuzzy Inference Systemsدریافت

سيستم استنتاج فازي

سيستمي كه يك نگاشت از ورودي به خروجي را با استفاده از منطق فاز فرموله ميكند به نام سيستم استنتاج فازي (FIS) شناخته مي شود. سيستم استنتاج فازي همچنين به نام سيستم مبتني بر قواعد نيز ناميده مي شود .زيرا اين سيستم ها از تعدادي عبارت « اگر – آنگاه » ساخته شده است. وقتي چنين سيستم هايي در نقش كنترلي ظاهر مي شوند به آنها كنترل كننده های فازی می گويند .معماري اصلي FIS از پنج بلوك تابع تشكيل شده كه در شكل زير نشان داده شده است:

بلوک های سازنده سیستم استنتاج فازی

پايگاه قواعد ( Rule base) : شامل قواعد و عبارات «‌اگر – آنگاه » فازي

پايگاه داده (Dara base) : تعريف توابع عضويت

واحد تصميم گيري ( Decision making unit)‌: انجام عمليات روي قواعد فازي

رابط فازي ساز ( Fazzification inter face)‌: تبديل ورودي هاي حقيقي به مجموعه هاي فازي

رابط غير فازي ساز ( Defazzification  inter face)‌ : تبديل نتايج فازي به مقادير حقيقي

دو واحد پايگاه داده و پايگاه قواعد با هم تحت عنوان پايگاه دانش (Knowledge base) شناخته مي شوند. سيستم هاي استنتاج فازي را مي توان به سه كلاس « ممداني (mamdani) » ، «‌سوگنو (sugeno) » و «‌تاكاگي (Takagi)» تقسيم كرد.

بسياري از FIS ها از نوع ممداني هستند كه در اين نوع ، اعضاي مجموعة فازي خروجي را پيش بيني مي كنند . 

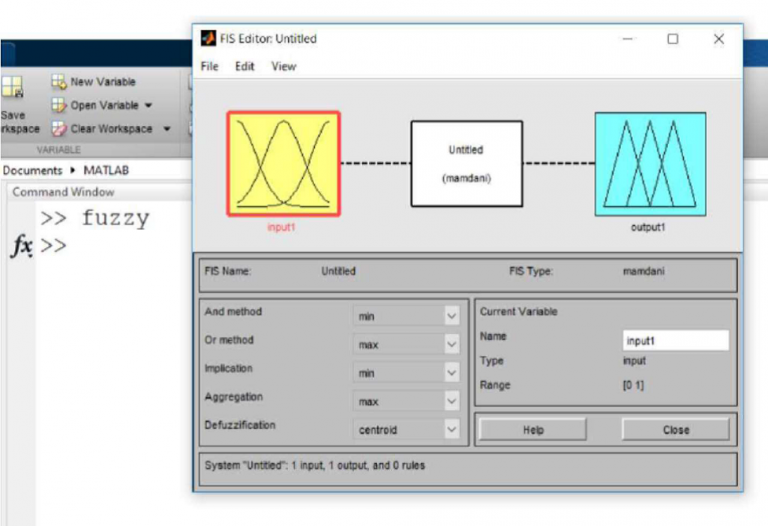
برای کار کردن با بخش فازی در Matlab درخط فرمان متلب عبارت fuzzy<< را تایپ کنید و یا  در بخش command  کلمه fuzzy  را تایپ کرده اینتر میزنیم .صفحه ای به صورت زیر باز می شود .

شروع به کار متلب برای قسمت فازی

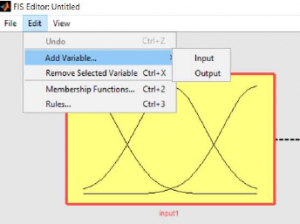
 تعریف متغیر ها

در این صفحه از طریق منوی Edit  تعداد ورودی ها و خروجی های مورد نظر را وارد می کنیم .با وارد کردن ورودی ها و خروجی ها به شکل زیر می رسیم.

افزودن متغیر ورودی و خروجی در متلب

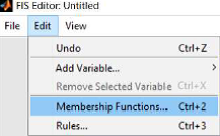
 تعریف توابع عضویت

بعد از تعیین ورودی ها و خروجی ها باید تابع عضویت را برای هر یک از آنها تعین کنیم برای این منظور از منوی Edit  وارد قسمت membership function  می شویم و با کلید روی هر متغیر تابع عضویت آن را تنظیم می کنیم . در زیر نمای بخش membership function آمده است . توابع عضویت را با استفاده از المان های موجود می توان تغییر داد.

تعریف توابع عضویت

از قسمت Type میتوان نوع تابع عضویت را تغییر داد و از قسم params میتوان پارامترهای مربوط به تابع عضویت را تغییر داد:

تغییر پارامترهای عضویت

تعریف rule ها

بعد از تعی ن membership function باید Ruleها را تعریف کنیم. برای این کار از منوی edit وارد قسمت Rule شده و شروع به تعریف Rule ها می کنیم.  

تعریف رول ها

 بررسی

بعد از تعریف Rule ها نوبت به بررسی نتایج می رسد . برای بررسی نتایج از منوی view گزینه Rules را انتخاب می کنیم و در صفحه باز شده متغیرها و حاصل آنها را بر روی خرو جی ها می توان مشاهده کرد.

دیدن خروجی

برای دیدن نمودارهای حاصل از بخش view قسمت Surface را انتخاب می کنیم .

منبع

 

سیستم استنتاج فازی چیست؟ قسمت 1

سیستم استنتاج فازی چیست؟ قسمت 2

/2 دیدگاه /توسط

منطق فازی در هوش مصنوعی

مقدمه

منطق فازی شاید بیشترین امید به پیشرفت و شتاب در جامعه هوش مصنوعی در تاریخچه اخیر آن باشد. اما چرا بعضی واژه های نامعلوم به درستی پشت واژه « فازی» قرار می گیرند؟ چرا « فازی » موجب پیشرفت هوش مصنوعی می شود؟
پاسخ این سوالات در مقاله زیر داده شده است.

تاریخچه منطق فازی

Fuzzy logic یک نوع منطق است که روش های متنوع نتیجه گیری در مغزبشر را جایگزین الگوهای ساده تر ماشینی می کند. مفهوم منطق فازی نخستین بار درجهان، توسط دانشمند برجسته ایرانی، پروفسور لطفی زاده، پروفسور دانشگاه برکلی در کالیفرنیا در سال 1965 ارائه گردید و نه تنها به عنوان یک متدولوژی کنترل در حوزه هوش مصنوعی ارائه شد، بلکه راهی برای پردازش داده ها، بر مبنای مجاز کردن عضویت گروهی کوچک، به جای عضویت گروهی دسته ای، ارائه کرد.
به عبارتی پروفسورلطفی زاده اینطور استدلال کرد که مغز بشر به ورودی های اطلاعاتی دقیق نیازی ندارد، بلکه قادراست تا کنترل تطبیقی را به صورت بالایی انجام دهد و این در مورد ماشین نیز صادق است.

منطق فازی چیست؟

ساده ترین تلقی برای تعریف منطق فازی این است که ” منطق فازی جواب یک سوال را به جای تقسیم به دو بخش درست یا نادرست،در اصل به یک محدوده جواب در این بین توسعه داده است”. نمونه معمول آن،وجود رنگ خاکستری در طیف رنگی بین سیاه و سفید است.
اما دایره عمل منطق فازی،از این هم گسترده تر است و می توان با استفاده از قواعد منطق فازی ، جواب های فازی متناسب با پرسش را ارائه نمود. برای مثال، جمله ” زمانی که باران می بارد، شما خیس می شوید” جمله نامفهومی نمی باشد، اما جمله ” زمانی که مقداری باران می بارد، شما مقداری خیس می شوید” می تواند از نظرمقدار بارش باران یا مقدار خیس شدن ، واژه های مختلفی را به جای واژه ” مقداری ” بپذیرد.

واژگانی از قبیل { کم ، زیاد، خیلی کم ، خیلی زیاد، قدری و … } این واژه ها واژه های زبان شناختی نام دارند، یعنی با مقادیر ریاضی نمی توان مقدار مشخصی را به آنها ربط داد.
اینجاست که منطق فازی وارد عمل می شود و با استفاده از مجموعه های فازی،برای متغیر میزان بارش باران، مجموعه ای را به شکل زیر صورت می دهد:
میزان بارش باران= { کم ، زیاد، خیلی کم ، خیلی زیاد، قدری و … }

باید پذیرفت قواعدی نظیر این زیبا هستند، زیرا این ها قواعد بشری هستند. آنها نمونه خوبی هستند برای اینکه ما چطورفکر می کنیم و چطور نتیجه می گیریم. بیایید به سراغ نمونه دیگری برویم:
ازشما سوال می شود” آیا شغلتان را دوست دارید؟” پاسخ شما لزوماً بله یا خیر نمی باشد؛ بنابراین مجموعه جواب به صورت زیر خواهد بود:
جواب= { تا حدی، نه خیلی، تقریباً، اصلاً ، کم و بیش، خیلی و… }
به هر یک از این مقادیر،مقداری به عنوان ” درجه عضویت” نسبت داده می شود، بدین معنا که مقدار مربوطه تا چه حد در این مجموعه عضو می باشد.

مجموعه های فازی و زبان طبیعی

لازم به ذکر است، در مجموعه های قطعی، یک شیء قطعاً ، یا عضو مجموعه، است یا نیست:

اگر xعضو مجموعه A باشد
اگر X عضو مجموعه A نباشد

اما در مجموعه های فازی، یک شیء می تواند تا حدودی به یک مجموعه متعلق باشد:

که در این حالت تابع عضویت، یک عدد حقیقی است:

بدین معنا که شیء مورد نظر به طور نسبی در یک مجموعه وجود دارد. همچنین مقدار جزئی تابع عضویت، درجه عضویت نامیده می شود.
از سوی دیگر در نظر داشته باشید: مفاهیم ومجموعه های فازی ،عموماً در زبان طبیعی بکار می روند نظیر:
” جان قد بلند است.”
” هوا گرم است.”

کلمات مشخص شده، به اسامی مقداری و مجموعه های فازی اشاره دارند. به عبارتی دیگر گزاره فازی که شامل لغاتی نظیر ” بلند” و ” گرم ” است، نشان دهنده مجموعه فازی مربوطه است. برای روشن شدن مفهوم ، مجموعه فازی بلند می تواند از تابع عضویت زیر بهره بگیرد:

پایین

قدری

تقریباً

متوسط

کم

بین

بالا

زیاد

به مقدار زیاد

خیلی

بیشتر

اصلاً

بیشترین

کم و بیش

در حدود

دراین تئوری، عضویت اعضای مجموعه از طریق تابع U ( X) مشخص می شود که X نمایانگر یک عضو مشخص و U تابعی فازی است که درجه عضویت X در مجموعه مربوطه را تعیین می کند و مقدار آن بین صفر و یک است:

همچنین به عنوان یک مجموعه متناهی از عناصر، برای عبارت بلند قد می توان زیر مجموعه فازی ذیل را تعریف کرد:
{ ( 8،1 )، ( 1، 705 )، ( 1، 7 )، (875،65 )، ( 05، 6 )،( 0125، 55 )،(0 ، 5 )}= بلند قد
در این مجموعه فازی، علامت “، ” درجه عضویت را از اعداد مربوطه به قد افراد جدا می سازد.

متغیرهای زبانی

” متغیرهای زبانی، متغیرهایی هستند که مقادیرشان اعداد نیستند،بلکه لغات یا جملات یک زبان طبیعی یا ساختگی هستند.”
به طورکلی، متغیرها به 2 دسته تقسیم می شوند:
زبانی: مانند کلمات و عبارات مربوطه به یک زبان طبیعی می باشد.
عددی: که متغیرها دارای مقادیرعددی هستند.

یک متغیر زبانی در واقع، یک عبارت زبان طبیعی است که به یک مقدار کمیت خاص اشاره دارد و اصطلاحاً مانند مترجم عمل می کند و به کمک تابع عضویت ،نشان داده می شود. مانند واژه ” سرد” در جمله ” هوا سرد است”. در اینجا سردی خود متغیری است برای دمای هوا که می تواند مقادیر مختلفی به خود اختصاص دهد و در واقع یک تابع عضویت برای آن تعریف می شود.

درعین حال متغیرهای زبانی می توانند از الحاق تشکیل شوند که هر کدام از uiها، عباتی تجزیه ناپذیر است. مانند ” تا حدی سرد “، که در مجموع به 4 دسته زیر تقسیم می شود:
عبارات اصلی: که به عنوان برچسب هایی برای مجموعه های فازی در نظر گرفته می شوند و مانند ” سرد” در عبارات بالا، یا عباراتی از قبیل : کوتاه، بلند و … که هر کدام تابع عضویت مخصوص خود را دارند.

حروف ربط: مانند و، یا…
پیراینده: که روی عبارات اولیه اعمال شده و اثر تشدید یا تضعیف در مفهوم آن عبارت را به همراه دارد. مانند تا حدی، اندکی ، بسیار و …
حروف نشانه: مانند پرانتز و …
بنابراین از مجموعه های فازی و متغیرهای زبانی، می توان برای کمیت بخشیدن به مفاهیم زبان طبیعی استفاده کرد.
چند متغیر زبانی و مقادیر نوعی که ممکن است به آنها اختصاص یابد:

متغیر زبانی

متغیر قابل پذیرش

ارتفاع قد
تعداد
مراحل زندگی
رنگ
روشنی
دسر

کوتوله، کوتاه، متوسط، بلند، خیلی بلند
تقریباً، هیچ، چند تا، کمی ، تعداد زیاد،
نوزاد، نوپا، کودک، نوجوان، بالغ
قرمز، آبی، سبز، زرد، نارنجی
تاریک، تیره، معمولی، روشن، سیر
کلوچه، کیک ، بستنی

اما چگونه منطق فازی به کار گرفته می شود؟

منطق فازی معمولاً از قوانین ” اگر و آنگاه” ( IF/THEN) استفاده می کند، اما این بررسی ،به صورت بررسی مقادیر خشک منطق کلاسیک نمی باشد، بلکه این بررسی توسط متغیرهای معنایی صورت می گیرد.این قوانین معمولاً به شکل زیر بیان می شود:
اگر( متغیر ) ( حالت ) است، آنگاه ( عملکرد ).

برای مثال ،یک دستگاه تنظیم کننده درجه حرارت را در نظر بگیرید که قانون منطق فازی را می توان اینگونه برایش تعریف کرد:
● اگر ( درجه حرارات) ( بسیار سرد) است، آنگاه ( فن را متوقف کن ).
● اگر درجه حرارت سرد است، آنگاه سرعت فن را کم کن.
● اگر درجه حرارت متعادل است، آنگاه همین سرعت فن را حفظ کن.
به طورکلی روش کار منطق فازی را می توان به شکل زیر نشان داد:

منطق کلاسیک

کاربرد هوش مصنوعی

هدف هوش مصنوعی، نزدیک نمودن رفتار و پاسخ یک سیستم کامپیوتری به الگوهایی است که انسان بر اساس آن ها رفتار می کندو پاسخ می دهد. در حقیقت گاه سیستم های طراحی می شوند که قدرت تجزیه و تحلیل آنها از انسان بیشتر است، ولی همچنان از الگوی ما استفاده می کنند. بر همین مبنا، هوش مصنوعی، با سیستم فازی یا سیستمی که انسان بر طبق آن تصمیم می گیرد،رابطه تنگاتنگی دارد.

قاعده Soft Computing

این قاعده کلیدی، عبارت است از بهره گیری از خطای مجاز به خاطر عدم دقت، نامعلومی، حقایق جزء به جزء برای دست یابی به قدرت و سهولت و یافتن راه حل با هزینه کم. البته ایده اساسی این قاعده، با بسیاری از توانایی های اولیه تئوری مجموعه های فازی، پیوند دارد.
همچنین هوش مصنوعی کلاسیک، بر روی دقت ارائه سیستم های مصنوعی متمرکز شده بود، اما با عملی کردن و رشد این سیستم ها ، مشخص شد که نمی توان منطق محض را در کاربردها به کار بست.

در واقع بر همین مبناست که منطق فازی به خوبی نشان می دهد که چرا منطق دو ارزشی < صفر و یک > در ریاضیات کلاسیک، قادر به تبیین و توصیف مفاهیم نادقیقی همچون < گرما و سرما> که مبنای بسیاری از تصمیم گیری های هوشمند را تشکیل می دهند ، نیست.
این در حالیست که نحوه استنتاج سیستم های هوشمند با استفاده از منطق فازی، به سرعت باعث پیشرفت این علم شد و باعث شد تا هوش مصنوعی ،حقیقتاً در جهشی فوق العاده ،به هوش انسانی نزدیک تر گردد.

زمینه های کاربرد منطق فازی درهوش مصنوعی

● هوش مصنوعی رویداد گرا: در این نوع، سیستم بر اساس هر رویدادی که انجام می شود، یک واکنش هوشمندانه انجام می دهد. در این حالت با استفاده از قواعد IF/THEN فازی، می توان برای حالات و رویدادهای جزء شده و طبقه بندی شده ،عکس العمل مناسبی تعیین کرد.
● هوش مصنوعی هدف گرا: این نوع هوش مصنوعی،هدف با ارزش بیشتر را بر می گزیند و آن را با تقسیم به زیرهدفهای کوچکتر، پردازش می کند.
در این نوع هوش نیز با کمک منطق فازی می توان با توجه به درجه عضویت، هدف مورد نظر را انتخاب کرد.

نمونه هایی از کاربرد عملی منطق فازی در هوش مصنوعی

جهت ملموس شدن بحث منطق فازی،دراین بخش به تعدادی از ادوات و ماشین هایی که بر اساس منطق فازی طراحی و به بازار عرضه شده اند اشاره می شود. ناگفته نماند در حال حاضر در بازار، نمونه هایی از این دستگاه ها، از نوع فاقد منطق فازی وجود دارد که به آنها صفت انواع عادی را اطلاق می کنیم، ضمن اینکه در اینجا قطعاً بحث بر سرنمونه های دارای منطق فازی و نحوه عملکرد این ماشین ها در طیف و محدوده این منطق می باشد.

● ماشین لباسشویی که استراتژی شستشو را براساس تشخیص میزان چرک، نوع پارچه، اندازه بارگیری، و میزان آب تنظیم می کند.
● دستگاه های تهویه مطبوع
● سیستم تشخیص گلف که چوب گلف را براساس فیزیک بدنی و ضربات گلف باز انتخاب می کند .
● شبکه عصبی برای تنظیم علایق و چشایی کاربران.
● سیستم کنترل کامپیوتر از طریق مغز
● هوش مصنوعی بازی های تصویری و جلوه های ویژه سینمایی
● قطارهای هوشمند
● ربات های هوشمند از جمله ربات ظرف شو

نتیجه

دریک کلام،منطق فازی معتقد است که ابهام همیشه و همواره در جوهره و ماهیت علم بوده و می توان از آن بهره جست. برخلاف آنچه اکثراً معتقدند که باید تقریب ها را دقیق تر کرد تا در نتیجه آن بهره وری افزایش یابد.ضمن اینکه در منطق فازی باید به دنبال ساختن ماشین آلات و مدل هایی بود که ابهام را به عنوان بخشی از سیستم ،هضم نموده و مدل کند.
زیرا تنها در این صورت است که می توان در سیستم های مبتنی بر هوش مصنوعی، رفتار و عکس العمل این گونه سیستم ها را به رفتار انسانی نزدیک نموده و به نتیجه دلخواه دست یافت.
بر همین اساس کاربرد منطق فازی در حل مسائل هوش مصنوعی،بیش از پیش درحال گسترش است. البته باید توجه داشت که مسائل بسیاری وجود دارند که حل آنها جز با انجام محاسبات دقیق ریاضی و پردازش حجم زیادی از داده ها ممکن نیست.

در نتیجه چنین به نظر می رسد که تلفیق منطق ” دو ارزشی و منطق فازی” بتواند توان عملیاتی کامپیوترها و بسیاری از تجهیزات و ادوات مورد استفاده بشر را، به میزان چشمگیری افزایش دهد و سهم مهمی در پیشرفت هوش مصنوعی تا حد نزدیک به هوش انسان ،داشته باشد.

منبع

/0 دیدگاه /توسط

منطق فازی (Fuzzy Logic) قسمت 1

در سال 1965 توسط دکتر لطفی زاده معرفی شد.
منطق فازی در واقع میگه که یه گزاره لزومی نداری یا درست باشه یا غلط (صفر باشه یا یک) ممکنه مثلا یه گزاره 0.7 درست باشه!
درکش یه مقدار در ابتدا سخته! بگذارید یه مثال بزنم، شما از دوستتون می پرسید بنظرت حسین بلنده یا نه؟ دوستتون جواب میده ایییی، بلند نیست اما کوتاه هم نمیشه بهش گفت! اما در منطق باینری (یا منطقی که اکثر ما باهاش تو کامپیوتر آشنا هستیم) هیچ وقت برای یه گزاره همچین جوابی نمیده.
توی منطق باینری ما میگیم اگه قد مساوی یا بلند تر از 175 بود بگو بلند اگه کوتاه تر بود بگو کوتاه! اما آدم اینطوری نیست منطقش مثل مثال قبلی که زدم.
حالا این سوال پیش میاد که ما در حال حاضر از همین منطق باینری جواب های خیلی خوبی میگیریم، فازی به چه دردی میخوره؟
برای جواب به این سوال یه مثال دیگه میزنم! مثلا یه شرکت می خواد یه کارخونه بزنه در فاصله ی ماکزیمم 200 کیلومتری تهران، که به تولید کننده ی یه مدل مواد اولیه نزدیک تر از 10 کیلومتر باشه و قیمت زمین هم اونجا هر چی کمتر باشه بهتر.اول یه بار با منطق باینری میریم پیش، اولین نمونه فاصلش با تهران 190 هست و با مواد اولیه هم 9 کیلومتر فاصله داره و قیمت زمین هم اونجا 2000 واحد هست، چندین تا نمونه دیگه هم برسی میشن که دو شرط اول رو ندارن، در آخر هم یه نمونه پیدا میشه که فاصلش تا تهران 201 کیلومتر هست و فاصلش با مواد اولیه 3 کیلومتره و قیمتش هم 1000 واحده! طبق منطق باینری این نمونه رد میشه چون فاصلش 201 هست و بیشتر از 200! اما حالا فرض کنید خود شما دارین تصمییم میگیرین، می یاین می بینید دو شرط آخر این مورد خیلی بهتر از اولین نمونس و تنها مشکل شرط اوله که 1 کیلومتر بیشتر از اون چیزیه که میخواین، با خودتون میگید خوب 1 کیلومتر در مقابل اون شرایط خوب که چیزی نیس و این مورد آخر رو انتخاب می کنید!
منطق فازی دقیقا همینو میگه! یعنی مثل منطق باینری که کاملا سخت گیرانه شرایط رو چک میکنه عمل نمی کنه بلکه مثل مغز آدم انعطاف پذیره.
این روزا تو خیلی چیزها از منطق فازی استفاده میشه، مثلا چند تاشون که شاید جالب باشن اینان:

  • ترمز های ABS و سیستم کروز.
  • دوربین ها
  • ماشین ظرف شویی
  • آسانسور ها
  • ماشین لباس شویی
  • بازی های رایانه ای
  • شناخت الگو ها
  • سیستم های تهویه

فکر کنم تقریبا فایده ی منطق فازی جا افتاده باشه. برای شروع استفاده از منطق فازی باید یه سری مفاهیم اولیه رو یاد بگیریم.
ببینید منطق فازی در واقع یه راه ساده برای رسیدن به یه نتیجه ی قطعی هستش بر اساس ورودی های ناقص، خطادار یا مبهم! از یه سری قانون خیلی ساده هم پیروی می کنه:

کد پی‌اچ‌پی:
IF x AND y THEN z
IF a OR b THEN c

همونطور که می دونید if در زبان برنامه نویسی چیز جدیدی نیست! اما با یه مثال ساده شاید بشه فرقش رو نشون داد.
در نظر بگیرید دارید یه سیستم تهویه طراحی می کنید، توی سیستم های فازی بجای استفاده از شرط هایی مثل temprature>60C یا 30C<temprature<60C از اصطلاحات زیر استفاده می کنیم:

کد پی‌اچ‌پی:

IF temperature IS very cold THEN stop fan

IF temperature IS cold THEN turn down fan

IF temperature IS normal THEN maintain level

IF temperature IS hot THEN speed up fan

دقیقا مثل وقتی که شما توی ماشین نشستین، می بینید هوا خیلی گرمه بدون اینکه دمای دقیق توی ماشین رو بدونید کولر ماشین رو روشن می کنید و روی دمای کم میگذارید!
اگر دقت کنید هیچ ELSEای وجود نداره، چون دما می تونه هم سرد باشه هم متوسط با درجه های مختلف!
اپراتور های AND، OR و NOT که باهاشون توی منطق باینری آشنا هستیم توی منطق فازی هم وجود دارن.
قبل از تعریف این عملگر ها باید بدونیم مجموعه های فازی یا Fuzzy sets به چه معنی هستند. همونطور که گفتیم توی منطق فازی درجه ی درستی لزوما نباید 0 یا 1 باشه و یه گزاره می تونه مثلا 0.3 درست باشه.
بعد گفتیم که تو منطق فازی می تونیم از هوای گرم یا قد بلند صحبت کنیم، اما باید اول اونارو برای سیستم فازیمون تعریف کنیم! هر کدوم از این دسته ها یه مجموعه ی فازی رو تشکیل میدن.
در واقع یه مجموعه ی فازی یه جفت (A, m) هست که A یه مجموعه هست و m یه تابع با دامنه ی A و برد [0,1]. به ازای هر x عضو (A، m(x درجه ی عضویت یا درستی x رو نشون میده!
می دونم یه کلمه از چند تا جمله ی قبل نفهمیدین الان بصورت نمودار میبینیدشون و می فهمید که چیز خیلی پیچیده ای نیست!
خوب حالا که تعریف فازی ست هارو فهمیدیم میریم که اونارو توی نمودار ببینیم و عملگر هارو هم از روی شکل و با توجه به تعریفشون بررسی کنیم:
[عکس: 6.gif]
به عنوان مثال این شکل مجموعه ی فازی جوان رو نشون میده، شما وقتی از دوستتون می پرسین بنظرت علی جوونه؟
دوستتون اگه علی 17 سالش باشه میگه آره، اگه 25 سالش باشه میگه اییی، آره هنوز میشه بهش گفت جوونه، اگه 28 سالش باشه میگه خیلی جوون نیس و اگه 50 سالش باشه میگه نه!
این مجموعه ی فازی هم در واقع همین رو میگه! همونطور که میبینید قبل از 20 سال (m(B یک هست، یعنی 0 تا 20 کاملا عضو مجموعه ی جوان هست، هر چی که میریم جلوتر عضویت توی مجموعه ی جوانی کمتر شده، توی 25 سالگی درجه ی عضویت یا درستی 0.5 هست و توی 28 سالگی 0.2 و بعد از 30 سالگی 0 که یعنی از این سن به بعد اصلا جوان نیست!
بنظرم الان یکم بهتر مطلب جا افتاده باشه! حالا فرض کنید دو تا مجموعه ی فازی زیر رو داشته باشیم:
[عکس: 7.gif]
[عکس: 8.gif]
مجموعه ی اول رو در ابتدا در نظر میگیریم. تعریف NOT توی شکل بصورت زیره:
[عکس: 9.gif]
یا به عبارتی:

کد پی‌اچ‌پی:
NOT A = (1- m(A))

خوب حالا دو مجموعرو که بالاتر نمودارشون هست رو در نظر بگیرین، تعریف AND روی اون دو مجموعه بصورت زیره:
[عکس: 10.gif]
یا به عبارتی:

کد پی‌اچ‌پی:
A AND B = minimum(m(A), m(B))

OR هم قاعدتا تا الان حدس زدید به چه صورت خواهد بود:
[عکس: 11.gif]

کد پی‌اچ‌پی:
A OR B = maximum(m(A), m(B))[/list]

اینها مقدماتی بود از منطق فازی. البته اینا مفاهیم خیلی اولیه ی منطق فازی بودن، اما توی کار از همین مفاهیم خیلی ساده و ترکیبشون میشه نتایج خیلی عاقلانه ای گرفت.
ما تا اینجا فقط به پروسه ی Fuzzification پرداختیم! بعد از اینکه عملیات فازی روی سیستم انجام شد در نهایت یه جواب قطعی می خوایم. برای رسیدن به یه جواب قطعی از پروسه ی Defuzzification استفاده میشه.
منبع

منطق فازی

منطق فازی (fuzzy logic) اولین بار در پی تنظیم نظریهٔ مجموعه‌های فازی به وسیلهٔ پروفسور لطفی زاده (۱۹۶۵ م) در صحنهٔ محاسبات نو ظاهر شد.
واژهٔ fuzzy به معنای غیردقیق، ناواضح و مبهم (شناور) است.

کاربرد این بخش در علوم نرم‌افزاری را می‌توان به طور ساده این‌گونه تعریف کرد: منطق فازی از منطق ارزش‌های «صفر و یک» نرم‌افزارهای کلاسیک فراتر رفته و درگاهی جدید برای دنیای علوم نرم‌افزاری و رایانه‌ها می‌گشاید، زیرا فضای شناور و نامحدود بین اعداد صفر و یک را نیز در منطق و استدلال‌های خود به کار برده و به چالش می‌کشد. منطق فازی از فضای بین دو ارزش «برویم» یا «نرویم»، ارزش‌های جدید «شاید برویم» یا «می‌رویم اگر» یا حتی «احتمال دارد برویم» را استخراج کرده و به کار می‌گیرد. بدین ترتیب به عنوان مثال مدیر بانک پس از بررسی رایانه‌ای بیلاناقتصادی یک بازرگان می‌تواند فراتر از منطق «وام می‌دهیم» یا «وام نمی‌دهیم» رفته و بگوید: «وام می‌دهیم اگر…» یا «وام نمی‌دهیم ولی…».

مقدمه

دانش مورد نیاز برای بسیاری از مسائل مورد مطالعه به دو صورت متمایز ظاهر می‌شود:

۱. دانش عینی مثل مدل‌ها و معادلات و فرمول‌های ریاضی که از پیش تنظیم شده و برای حل و فصل مسائل معمولی فیزیک، شیمی، یا مهندسی مورد استفاده قرار می‌گیرد.
۲. دانش شخصی مثل دانستنی‌هایی که تا حدودی قابل توصیف و بیان زبان‌شناختی بوده، ولی امکان کمّی کردن آن‌ها با کمک ریاضیات سنتی معمولاً وجود ندارد. به این نوع دانش، دانش ضمنی یا دانش تلویحی (Tacit knowledge) گفته می‌شود.

از آن جا که در عمل هر دو نوع دانش مورد نیاز است منطق فازی می‌کوشد آن‌ها را به صورتی منظم، منطقی، و ریاضیاتی بایکدیگر هماهنگ گرداند.

تاریخچه

منطق فازی بیش از بیست سال پس از ۱۹۶۵ از درگاه دانشگاه‌ها به بیرون راه نیافت زیرا کمتر کسی معنای آنرا درک کرده بود. در اواسط دهه ۸۰ میلادی قرن گذشته صنعتگران ژاپنی معنا و ارزش صنعتی این علم را دریافته و منطق فازی را به کار گرفتند. اولین پروژه آنها طرح هدایت و کنترل تمام خودکار قطار زیرزمینی شهر سندای بود که توسط شرکت هیتاچی برنامه‌ریزی و ساخته شد. نتیجهٔ این طرح موفق و چشم‌گیر ژاپنی‌ها به طور ساده اینگونه خلاصه می‌شود: آغاز حرکت نامحسوس (تکان‌های ضربه‌ای) قطار، شتاب‌گرفتن نامحسوس، ترمز و ایستادن نامحسوس و صرفه جویی در مصرف برق.

از این پس منطق فازی بسیار سریع در تکنولوژی دستگاه‌های صوتی و تصویری ژاپنی‌ها راه یافت (از جمله نلرزیدن تصویر فیلم دیجیتال ضمن لرزیدن دست فیلم‌بردار). اروپایی‌ها بسیار دیر، یعنی در اواسط دههٔ ۱۹۹۰ میلادی، پس از خوابیدن موج بحث‌های علمی در رابطه با منطق فازی استفادهٔ صنعتی از آن را آغاز کردند.

ملاحظات آغازین

منطق فازی از جمله منطق‌های چندارزشی است و بر نظریهٔ مجموعه‌های فازی تکیه می‌کند. مجموعه‌های فازی، خود از تعمیم و گسترش مجموعه‌های قطعی به صورتی طبیعی حاصل می‌آیند.

مجموعه‌های قطعی

مجموعه‌های قطعی (Crisp sets) درواقع همان مجموعه‌های عادی و معمولی هستند که در ابتدای نظریهٔ کلاسیک مجموعه‌ها معرفی می‌شوند. افزودن صفت قطعی به واقع وجه تمایزی را ایجاد می‌نماید که به کمک آن می‌شود یکی از مفاهیم ابتکاری و حیاتی در منطق فازی موسوم به تابع عضویت را به آسانی در ذهن به وجود آورد.

در حالت مجموعه‌های قطعی، تابع عضویت فقط دو مقدار در برد خود دارد (در ریاضیات، برد یک تابع برابر با مجموعه تمام خروجی‌های تابع است).

آری و خیر (یک و صفر) که همان دو مقدار ممکن در منطق دوارزشی کلاسیک هستند؛ بنابراین:

{\displaystyle \mathbf {\mu } _{A}(x)=\left\{{\begin{matrix}1&{\mbox{if}}\ x\in A,\\0&{\mbox{if}}\ x\notin A.\end{matrix}}\right.}

که در اینجا {\displaystyle \mathbf {\mu } _{A}(x)} تابع عضویت عنصر x در مجموعه قطعی A است.

مجموعه‌های فازی

مجموعه‌های فازی (fuzzy sets) از تعمیم نظریهٔ کلاسیک مجموعه‌ها حاصل می‌آید که در منطق فازی کاربرد دارد.

برد تابع عضویت از {\displaystyle \{0,1\}} در مورد مجموعه‌های قطعی به بازهٔ بستهٔ {\displaystyle [0,1]} برای مجموعه‌های فازی تبدیل می‌شود.

متغیرهای زبانی

منطق فازی دما

متغیرهای زبانی به متغیرهایی گفته می‌شود که مقادیر مورد قبول برای آن‌ها به جای اعداد، کلمات و جملات زبان‌های انسانی یا ماشینی هستند.
همانگونه که در محاسبات ریاضی از متغیرهای عددی استفاده می‌گردد، در منطق فازی نیز از متغیرهای زبانی (گفتاری یا غیر عددی) استفاده می‌گردد. متغیرهای زبانی بر اساس ارزش‌های زبانی (گفتاری) که در مجموعه عبارت (کلمات/اصطلاحات) قرار دارند بیان می‌شود. عبارت زبانی (Linguistic terms) صفاتی برای متغیرهای زبانی هستند. به عنوان مثال: متغیر زبانی «سن» بسته به تقسیمات مورد نظر شخصی و شرایط می‌تواند مجموعه عباراتی از قبیل «نوجوان»، «جوان»، «میان سال» و «سالمند» باشد.

مجموعه عبارات (اصطلاحات) فازی (سن) = { «جوان»، «نه جوان»، «نه چندان جوان»، «خیلی جوان» ،… ، «میان سال»، «نه چندان میان سال»… ، «پیر»، «نه پیر»، «خیلی پیر»، «کم و بیش پیر»… ، «نه خیلی جوان و نه خیلی پیر»، «نه جوان و نه پیر»…}

یا در مثالی دیگر، فشار (خون) را می‌توان متغیری زبانی در نظر گرفت، که ارزش‌هایی (خصوصیت‌هایی) از قبیل پایین، بالا، ضعیف، متوسط و قوی را می‌تواند در خود جای دهد. به زبان ریاضی داریم (T = Terms):

{پایین، بالا، ضعیف، متوسط، قوی} = (فشار)T

توابع عضویت

درجه عضویت \mu _{{A}}(x) بیانگر میزان عضویت عنصر x به مجموعه فازی {\tilde A} است. اگر درجه عضویت یک عنصر از مجموعه برابر با صفر باشد، آن عضو کاملاً از مجموعه خارج است و اگر درجه عضویت یک عضو برابر با یک باشد، آن عضو کاملاً در مجموعه قرار دارد. حال اگر درجه عضویت یک عضو مابین صفر و یک باشد، این عدد بیانگر درجه عضویت تدریجی می‌باشد.

عدم قطعیت

صفت عدم قطعیت، به صورت‌های گوناگون، در همهٔ زمینه‌ها و پدیده‌ها صرف نظر از روش شناسی مورد کاربرد جهت مطالعه، طراحی، و کنترل پدیدار می‌شود.
مفاهیم نادقیق بسیاری در پیرامون ما وجود دارند که آن‌ها را به صورت روزمره در قالب عبارت‌های مختلف بیان می‌کنیم. به عنوان مثال: «هوا خوب است» هیچ کمیتی برای خوب بودن هوا مطرح نیست تا آن را بطور دقیق اندازه‌گیری نماییم، بلکه این یک حس کیفی است. در واقع مغز انسان با در نظر گرفتن عوامل گوناگون و بر پایه تفکر استنتاجی جملات را تعریف و ارزش گذاری می‌نماید که الگوبندی آن‌ها به زبان و فرمول‌های ریاضی اگر غیرممکن نباشد، کاری بسیار پیچیده خواهد بود. منطق فازی فناوری جدیدی است که شیوه‌هایی را که برای طراحی و مدل سازی یک سیستم نیازمند ریاضیات پیچیده و پیشرفته‌است، با استفاده از مقادیر زبانی و دانش فرد خبره جایگزین می‌سازد.

انگیزه‌ها و اهداف

برای مقابلهٔ مؤثر با پیچیدگی روزافزون در بررسی، مطالعه، مدل‌سازی و حل مسائل جدید در فیزیک، مهندسی، پزشکی، زیست‌شناسی و بسیاری از امور گوناگون دیگر ایجاد و ابداع روش‌های محاسباتی جدیدی مورد نیاز شده‌است که بیشتر از پیش به شیوه‌های تفکر و تعلم خود انسان نزدیک باشد. هدف اصلی آنست که تا حد امکان، رایانه‌ها بتوانند مسائل و مشکلات بسیار پیچیدهٔ علمی را با همان سهولت و شیوایی بررسی و حل و فصل کنند که ذهن انسان قادر به ادراک و اخذ تصمیمات سریع و مناسب است.

در جهان واقعیات، بسیاری از مفاهیم را آدمی به صورت فازی (به معنای غیر دقیق، ناواضح و مبهم) درک می‌کند و به کار می‌بندد. به عنوان نمونه، هر چند کلمات و مفاهیمی همچون گرم، سرد، بلند، کوتاه، پیر، جوان و نظائر این‌ها به عدد خاص و دقیقی اشاره ندارند، اما ذهن انسان با سرعت و با انعطاف‌پذیری شگفت‌آوری همه را می‌فهمد و در تصمیمات و نتیجه‌گیریهای خود به کار می‌گیرد. این، در حالی ست که ماشین فقط اعداد را می‌فهمد و اهل دقّت است. اهداف شیوه‌های نو در علوم کامپیوتر آن است که اولاً رمز و راز این‌گونه توانایی‌ها را از انسان بیاموزد و سپس آن‌ها را تا حد امکان به ماشین یاد بدهد.

قوانین علمی گذشته در فیزیک و مکانیک نیوتونی همه بر اساس منطق قدیم استوار گردیده‌اند. در منطق قدیم فقط دو حالت داریم: سفید و سیاه، آری و خیر، روشن و تاریک، یک و صفر و درست و غلط.

متغیرها در طبیعت یا در محاسبات بر دو نوعند: ارزش‌های کمی که می‌توان با یک عدد معین بیان نمود و ارزش‌های کیفی که براساس یک ویژگی بیان می‌شود. این دو ارزش قابل تبدیل‌اند.
مثلاً در مورد قد افراد، اگر آن‌ها با ارزش عددی (سانتی‌متر) اندازه‌گیری نماییم و افراد را به دسته‌های قدکوتاه و قدبلند تقسیم‌بندی کنیم و در این دسته‌بندی، حد آستانه ۱۸۰ سانتی‌متر برای بلندی قد مدنظر باشد، در اینصورت تمامی افراد زیر ۱۸۰ سانتی‌متر براساس منطق قدیم قد کوتاه‌اند. حتی اگر قد فرد ۱۷۹ سانتی‌متر باشد؛ ولی در مجموعه فازی هر یک از این صفات براساس تابع عضویت تعریف و بین صفر تا یک ارزشگذاری می‌شود.

از آن جا که ذهن ما با منطق دیگری کارهایش را انجام می‌دهد و تصمیماتش را اتّخاذ می‌کند، جهت شروع، ایجاد و ابداع منطق‌های تازه و چندارزشی مورد نیاز است که منطق فازی یکی از آن‌ها می‌باشد.

کاربردهای صنعتی

برای هر دستور کار و خواسته عمل‌کرد مکانیکی، الکترومغناطیسی یا نرم‌افزاری و غیره که برای آن فرمول یا دستورالعمل مطلق و شفاف ریاضی وجود نداشته باشد و به‌ویژه زمانی که دستور کار به‌وسیلهٔ جملات انشاء شده باشد، نرم‌افزار متکی به منطق فازی راه‌گشا و کارآمد است.

برخی از کاربردها عبارتند از:

  • هدایت و کنترل هرگونه دستگاه و تأسیسات پویا و حرکت‌ساز را می‌توان با کمک منطق فازی به بهترین وجه اعمال نمود. از جمله ماشین لباس‌شویی، قطارها، ترمز ای‌بی‌اس خودرو،آسانسور، جرثقیل، تسمه نقاله، موتورهای احتراقی، نشست و برخاست خودکار هواپیما و غیره.
  • دستگاه‌های سمعی/بصری دیجیتال.
  • «آینده‌نگری» نرم‌افزارها جهت جلوگیری از هنگ کردن سرورها، کنترل موتورهای جستجوگر در اینترنت، سیستم‌های نرم‌افزاری ترجمه، رباتیک و هوش مصنوعی، بررسی احتمال برداشت‌هایسرندیپیتی، مهندسی پزشکی از جمله آسیب‌شناسی یا هدایت و کنترل تأسیسات سی تی اسکن، سی سی یو و آی سی یو، دستگاه ضربان‌ساز قلب.
  • کارهای ریسک شناسی، آماری و ارزیابی بانکی جهت تصمیم‌گیری‌های مدیران.
  • محاسبات آماری بیمه‌ها برای یافتن فاکتورهای ریسک در قراردادها. (بسیاری از شرکت‌های بیمه در جهان، ارزیابی صدمات و طلب خسارت مشتریان را چند سالی است بوسیله نرم‌افزارهای فازی پوشش می‌دهند و از این راه با تقلب و کلاه‌برداری‌های مشتریان مبارزه می‌کنند)

نرم‌افزارهای برای سیستم منطق فازی

  • Peach محاسبات هوشمند در پایتون
  • DotFuzzy کتابخانهٔ متن‌باز منطق فازی سی شارپ
  • JFuzzyLogic بستهٔ نرم‌افزاریِ متن باز منطق فازی برای جاوا
  • بسته pyFuzzyLib کتابخانهٔ منطق فازی در پایتون
  • بسته pyfuzzy کتابخانهٔ منطق فازی در پایتون
  • FisPro سیستم استنتاج فازی حرفه‌ای
  • (KBCT (Knowledge Base Configuration Tool ابزار پیکربندی پایگاه اطلاعات

منبع

منطق فازی (Fuzzy Logic) قسمت 1
منطق فازی (Fuzzy Logic) قسمت 2

/0 دیدگاه /توسط

پردازش و قطعه بندی تصاویر رنگی

چکیده

پردازش اطلاعات چند کاناله در رنج های متفاوتی از کانال اطلاعات است که در آن پردازش اطلاعات دارای زمان زیاد و پیچیدکی فضایی بالایی بعلت تنوع و گستردگی داده ها می باشد. در این راستا بیشتر رویکردهای کلاسیک از فیلترینگ و روشهای کلاسیک استفاده می کنند. برخی از این روشها مدل تصادفی مارکوف ، فیلترینگ بردار جهت دار و مدل های ترکیبی آماری شبیه گوسین و دیریکله هستند . رویکردهای غیر کلاسیک  شامل عصبی،فازی و ژنتیک می شوند.در این مقاله رویکر دهای نامبرده شده را برای ارتقای تصاویر رنگی و قطعه بندی بهتر آنها شرح می دهیم.

کلمات کلیدی: ارتقای تصاویر رنگی ، قطعه بندی تصاویر رنگی ، رویکردهای غیر کلاسیک، رویکرهای غیر کلاسیک

مقدمه

پردازش اطلاعات چند کاناله یکی از مفروضات مهم برای ارزیابی فیلدهای نمایش از راه دور  GIS، تصویر برداری بیو مدیکال ، مدیریت دادهای چند طیفی ، بازیابی و تحلیل ویژگیها ی اشیاء از قبیل رنج های مختلف کانال اطلاعات که بطور اساسی پیچیده هستند. و این پیچیدگی بدلیل گسترده گی داده های ارسالی و اصلی آن می باشد . به بیانی ساده تر پردازش و قطعه بندی رنگی تصاویر به صورت مثالهای کلاسیک از پردازش اطلاعات چند مجرایی هستند. یک چالش ابتدایی در پردازش تصاویر تنوع و گستردگی از شدت رنگهای گاموت با پردازش مشخصه های چند طیفی از اجزای رنگی متفاوت آنها می باشد.

نسبت ها ی محاسباتی وابسته به اجزای رنگها ، همبستگی ورودی و نمایش مشخصه های غیر خطی می باشد.

گام اصلی در پردازش تصاویر دیجیتالی 1-پیش پردازش داده ها برای آماده سازی داده ها برای ارتقای کنتراست ، کاهش نویز و یا فیلترینگ است. 2- استخراج ویژگیها برای بازیابی اطلاعات غیر زائد و با ارزش از یک تصویر.

این عملیات هدفی برای بدست آوردن زمان بهینه و کاهش نمونه داده هاست که توسط کشف، تمرکز و معین کردن موقعیت ها و جایگاهی و تطبیقی از اشیاء است. اهداف بسیاری از الگوریتم های موجود اشیاء مورد اشاره هستند که هر از چند گاهی قابلیت استنتاج را پیدا می کنند .

به طور کلی مشخصه ها و بهینه سازی های یک الگوریتم توسط دامنه ای از داده های ورودی که قابلیت پردازش را دارند معین می شوند. دامنه داده معمولی شامل پیکسل ها، ویژگیهای محلی و لبه های تصاویر، اشیاء ادغام شدنی و مقدار ناچیزی از نامها می شوند.

دامنه داده خروجی به طور ثابت شامل قطعات تصویر به طور همگن، لبه ها  پیدا شده روی اشیاء خاص از ناحیه های قطعات و اشیاء با اندازه ها، اشکال ، رنگ ها و اطلاعات متنی متفاوت می باشند.

مدل های رنگی متفاوت قابل فهم، شرط لازم برای پردازش تصاویر رنگی است. در این مقاله تمایز ها و زیان های قابلیت های فضاهای رنگی موجود را بررسی می کنیم. متغیرهای استاندارد فضای رنگی RGB مینمم پیچدگی فضای رنگی را استخراج می کنند و برای نمایش رنگ بکار می روند. کارایی هر یک از الگوریتم های قطعه بندی تصاویر هم از کلاسیک و غیر کلاسیک  را می توان با چندین رویکرد غیر نظارتی تشخیص داد.

به طور پیش فرض چند اندازه برای نمایش حالتها انتخاب می کنند مانند E که برای نمایش آنتروپی استفاده می شود. اندازه های مفید تجربی برای انعکاس قابلیت های قطعه بندی استفاده می شوند. اندازه های با مقادیر پائین قابلیت های بهتری از قطعه بندی را بدست می آورند.

رویکردهای کلاسیک در قطعه بندی و پردازش تصاویر رنگی

تکنیک های فیلترینگ برای حذف نویز و ارتقا لبه ها در سالهای اخیر به یک مسئله مهم و معروف تبدیل شده است. فلیتر بردار جهت دار (VDF) با در نظر گرفتن مقادیر سیگنال نقش مهمی در پردازش تصاویر عهده دار است. پردازش اندازه و جهت سیگنال در این کلاس از فیلتر های مستقل انجام می شود. فیلتر های چندگانه ارتقا لبه بر اساس بردار میانگین برای ارتقاء لبه های خفیف در تصاویر رنگی ارائه کردند. در این روش از سه زیر فیلتر (sub filter) استفاده می شود و سر انجام خروجی این زیر فیلتر ها با بردار میانگین مقایسه می شودو یک روش دیگر با توجه به نویز برای اطلاعات چندگانه فیلتر های نزدیکترین  همسایگی سازگار است. این فیلتر از ضرائب اطلاعات مستقل براساس یک روش اندازه گیری فاصله جدید که شامل بردار هاوی (جهت) فیلتر واندازه بردار فیلتر می باشد بهره می برد.

یک چهارچوب کاملا متفاوت را برای فیلتره ای رنگی ارائه می کنیم . این روش براساس رمز نگاری تصاویر رنگی و غیر رنگی کار می کنند . تا به حال چند رزولوشن بر اساس نظریه گراف ارائه شده است. این تکنیک بر اساس ویژگی و شباهت و ارتباط بین نواحی مشابه و ارتباط بین نواحی همسایه استفاده می کند و در نهایت برای اشیاء برای قطعه بندی ایده ال نواحی گروه بندی می شوند. ما می توانیم از مسائل خطی بجای مقادیر ویژه در مسائل قطعه بندی گراف استفاده کنیم . الگوریتم آنالیز میانگین شیفت دهی برای تخمین دقیق رنگ مرکز کلاسترهای فضای رنگ استفاده می کند. می توان همین روش را با استفاده از روش های پارتیشن بندی توسعه داد.

مدل های (MRF) برای مدل کردن وآنالیز عکس های چند طیفی استفاده می شود. چند جایگزین برای MRF پیشنهاد می شود تا پیچدگی زمانی آن را کاهش دهند . الگوریتم EM برای تخمین پارامترهای مدل های مخفی مارکوف برای کاهش وابستگی ساختاری در این روش استفاده می شود.  می توان این الگوریتم را برای تخمین پارمترهای مدل دوباره دسته بندی کرد. این تهمین از فاکتور جریمه برای داده های مستقل برای داده های مستقل برای ماکزیمم کردن احتمال کلی مجموعه داده ها و در نتیجه کاهش مرجع محاسبات استفاده می کنند.

چندین مدل ترکیبی آماری برای تخمین مناسب از توزیع ساختار عکس ارئه می شود. به عنوان مثال از مدل ترکیبی گوسین و مدل ترکیبی دیریکله می توان نام برد . مدل ترکیبی گوسین بدلیل لینکه خواص مشابهی دارد می تواند با توزیع داده ها بوسیله بردار میانگین  و ماتریس کواریانس ارائه شود . برای پیدا کردن راه حل  ماکزیمم  احتمال کلی برای قطعه بندی با استفاده از هسته جداگانه از این روش استفاده کردند. اگر چه این روش یک ساختار غیر گوسی و متقارن  را برای توزیع داده ها پیدا می کند . در این مسئله توزیع دیریکله همانند توزیع های تغییر یافته چند متغیره بتا می تواند به طور دقیق داده ها را انتخاب کند . از این مدل در تخمین هیستوگرام ها، مدل هاهی چند پردازشی تصویر و… استفاده می کنند.

رویکردها دیگر از پردازش و قطعه بندی تصاویر رنگی

بیشتر رویکردهای کلاسیک نیاز به دانش اولیه از داده ها ی تصویر برای پردازش تصویر و قطعه بندی آن و توزیع شدت های رنگ  اصلی و پارامترهای عملیاتی تصاویر دارند. در رویکردهای غیر کلاسیک که شامل  عصبی ،فازی، ژنتیک و wavelet می شوند نیازی به توزیع ها و پارمترهای عملیاتی ندارند. در این قسمت انواع این روشها را شرح می دهیم:

الف- روش های مبتنی بر شبکه های عصبی

در این روش از ساختار شبکه ی عصبی چند سطحی CNN برای پردازش تصاویر رنگی در مدل های رنگی RGB استفاده می شود. در این روش رنگ های اولیه یک سطح منحصر به فرد CNN می باشد که برای پردازش موازی بکار می رود. اخیرا ساختار CNN چند سطحی بر ای تصاویر رنگی در حال بررسی و استفاده می باشد.

از یادگیری رقابتی CL برای خوشه های رنگی مبتنی بر کمترین مجموع مربعات معیارها بکار گیری می شود.

Clهمگن  محلی برای خوشه بندی رنگی بهینه است. در مقایسه کارایی CLبا الگوریتم های خوشه بندی موجود شبیه CMA ,GCMA ,HCL می توان گفت که دو  روش GCMA ,HCL در مقابل شرط ابتدایی حساسیتی را از خود نشان نمی دهند نتایج GCMA اکثر مواقع بهینه است ولی دارای هزینه محاسباتی بالایی می باشد در مقابل HCL دارای هزینه محاسباتی کم می باشد ولی بهینه نیست. در نتیجه در خوشه بندی سریع از CL برای خوشه بندی داده ها استفاده می شود.

Som در بسیاری از موارد استفاده می شود در دامنه نظر به اینکه می تواند بازیابی کند محتوای رنگی برجسته را از تصاویر . به طور کلی از چندین شبکه som برای خوشه بندی مبتنی بر رنگ و ویژگیهای فضایی از پیکسل های تصاویر استفاده می شود. خروجی خوشه بندی، یک رویه مطلوب از قطعه بندی تصویر است.  Som تولید کرد نتایج خوشه بندی اولیه را مبتنی بر آموزش مجموعه ها از بردار 5 بعدی (R,G,B,x,y). تصاویر قطعاتی که توسط الحاق بلوکهای پراکنده و حذف پیکسل های ایزوله شده بوجود آمده اند. در یک مدل چند سطحی سازماندهی شبکه های عصبی (PSONN) بهینه است در استخراج رنگ های اشیاء از نویزهای رنگی تصاویر. بکارگیری معماری (PSONN) برای قطعه بندی رنگ ها  حقیقی تصاویر استفاده می شوند برای  چندین سطح از تابع های فعال سازی  مشخصه های تصاویر  توسط پارامترهای آستانه گیری ثابت و یکسان .

ب- رویکرد های مبتنی بر منطق فازی

تئوری مجموعه فازی و منطق فازی بکار گیری می شود به صورت دستی برای مقادیر وسیع از آشکار سازی خطای تخمینی در شدت گاموت تصاویر رنگی . الگوریتم FCM  یک روش جدید برای نشان دادن مرزهای مبهم بین خوشه ها می باشد.

الگوریتم  قطعه بندی تصاویر تکرار شونده در منطق فازی توسعه پیدا کرد . فضای رنگی  HSV مبتنی بر رویکرد فازی برای شناسایی رنگ ها اشیا در پشت زمینه های پیچیده بکارگیری شد که شامل روشنایی های متفاوت  می با شد. یک رویکرد دینامیکی فازی مبتنی بر خواص پیکسا های تصویر وجود دارد. توطعه پیدا کرد شبکه عصبی min-max بر پایه تکنیک های قعه بندی تصاویر (FMMSIS) برای کشف تصاویر مصنوعی. روش ارائه شده برای پیدا کردن مرزهای مینیمم مربعی (MBR) برای نمایش اشیاء در تصاویر بکار می رود.برچسب عصب فازی یک نمونه قابل توجیه مبتنی بر بردار تدریجی، الگوریتم  عصب گازی در جهت نماهای خوشه بندی است.

سیستم های فازی عصبی مبتنی بر یک نوع جدید از شبکه های عصبی مصنوعی هستند که  شبکه عصبی افزاینده وزن دار نامیده می شود (WINN). این سیستم ها  در سه گام عمل میکند: در ابتدا مجموعه داده های ورودی وزن دهی می شوند در شبکه . انعکاس پیدا می کنند و  شامل کاهش دهنده ها می شود .

در گام بعدی از نتایج وزن های اتصالات شبکه  برای رویه ی آب پخشان در مسائل تک بعدی استفاده می شود.تعدادی از جداکننده های اتصالات وزن دار زیر شبکه ها خوشه هایی را با یک زیر شبکه برای هر خوشه  بدست می آورد. در هر صورت همه ی گره های زیر شبکه دارای برچسب هستند. در نهایت نتایج خوشه ها بر روی مجموعه داده های مورد استفاده ورودی طبقه بنده های مجاور نگاشت می شود.رویکردها ی کاهش حافظه و  محاسباتی دارای data setهای بزرگی هستند.

ج- رویکردهای مبتنی بر الگوریتم ژنتیک

الگوریتم ژنتیک برای بهینه سازی پارامترهای ورودی در الگوریتم های قطعه بندی موجود مورد استفاده قرار می گیرد طبقه بندی کاربردهای الگوریتم ژنتیک در دو کلاس مهم برای قطعه بندی تصاویر استفاده می شوند:

 1) کاربرد پارامترهای انتخابی قطعه بندی برای استخراج قطعات خروجی

2) کاربرد پیکسل های سطحی قطعه بندی برای استخراج برچسب نواحی

روش های قطعه بندی موجود که نیاز به پارامترهای بهینه در طبقه بندی نخست دارند. الگوریتم ژنتیک برای وفق دادن 4 پارامتر ازالگوریتم قطعه بندی فونیکس استفاده می کند. الگوریتم ژنتیک در تکنیک های قطعه بندی غیر نظارتی راکه آستانه گیری چندگذر گاهی دارد را برای الگوریتم های متفاوت دسته بندی می کند. که این روش برای قطعه بندی اشیاء سه بعدی و دو بعدی مورد استفاده قرار می گیرد.در قطعه بندی سطوح پیکسل دار، الگوریتم ژنتیک را برای پیداکردن برچسب نواحی  مشخصه های پیکسل ها استفاده می کند.

د- wavelet

تحلیل چند کیفیتی (MRA)  برای نمایش سیگنالها و پردازش کیفیت نمایش سیگنالهای تقسیم کننده کیفیت وضوح و فضای مقیاس دهی استفده می شود. و معمولا برای کاهش ابعاد تصویر بکار گرفته می شود . تبدیل wavelet یک ابزار بهینه برای تخمین، فشرده سازی ،حذف نویز و پیدا کردن لبه ها است .می توان از این روش برای قطعه بندی تصاویر متنی نیز استفده نمود. ساختار wavelet بهینه است برای ساختارهای طیفی از داده های ورودی که اغلب برای استخراج ویزگی های تصاویر مورد استفاده قرار می گیرند.

نتیجه گیری

در این مقاله چندین الگوریتم مهم برای پیش پردازش و قطعه بندی تصاویر رنگی مورد بررسی قرار گرفت. روش های کلاسیک برای پردازش تصاویررنگی که دارای رنج تکنیک های فیلترینگ و مدل های آمار ی باشند مناسب هستند. روش های غیر کلاسیک مانند تکنیک های فازی ،عصبی ،ژنتیک وویولت تجدید پذیر هستند . کارایی این روش ها برای فاکتورهای گوناگون روی دادهای توزیع پذیر و پارامترهای عملیاتی و محیهای عملیاتی مورد بررسی قرار گرفتند.

نتیجه کلی که می توان از این مقاله گرفت این است که رنگ ها قابلیت آستانه گیری در قطعه بندی را دارند.

/0 دیدگاه /توسط