بایگانی برچسب برای: مدول فازی ساز

منطق فازی (Fuzzy Logic) قسمت 1

در سال 1965 توسط دکتر لطفی زاده معرفی شد.
منطق فازی در واقع میگه که یه گزاره لزومی نداری یا درست باشه یا غلط (صفر باشه یا یک) ممکنه مثلا یه گزاره 0.7 درست باشه!
درکش یه مقدار در ابتدا سخته! بگذارید یه مثال بزنم، شما از دوستتون می پرسید بنظرت حسین بلنده یا نه؟ دوستتون جواب میده ایییی، بلند نیست اما کوتاه هم نمیشه بهش گفت! اما در منطق باینری (یا منطقی که اکثر ما باهاش تو کامپیوتر آشنا هستیم) هیچ وقت برای یه گزاره همچین جوابی نمیده.
توی منطق باینری ما میگیم اگه قد مساوی یا بلند تر از 175 بود بگو بلند اگه کوتاه تر بود بگو کوتاه! اما آدم اینطوری نیست منطقش مثل مثال قبلی که زدم.
حالا این سوال پیش میاد که ما در حال حاضر از همین منطق باینری جواب های خیلی خوبی میگیریم، فازی به چه دردی میخوره؟
برای جواب به این سوال یه مثال دیگه میزنم! مثلا یه شرکت می خواد یه کارخونه بزنه در فاصله ی ماکزیمم 200 کیلومتری تهران، که به تولید کننده ی یه مدل مواد اولیه نزدیک تر از 10 کیلومتر باشه و قیمت زمین هم اونجا هر چی کمتر باشه بهتر.اول یه بار با منطق باینری میریم پیش، اولین نمونه فاصلش با تهران 190 هست و با مواد اولیه هم 9 کیلومتر فاصله داره و قیمت زمین هم اونجا 2000 واحد هست، چندین تا نمونه دیگه هم برسی میشن که دو شرط اول رو ندارن، در آخر هم یه نمونه پیدا میشه که فاصلش تا تهران 201 کیلومتر هست و فاصلش با مواد اولیه 3 کیلومتره و قیمتش هم 1000 واحده! طبق منطق باینری این نمونه رد میشه چون فاصلش 201 هست و بیشتر از 200! اما حالا فرض کنید خود شما دارین تصمییم میگیرین، می یاین می بینید دو شرط آخر این مورد خیلی بهتر از اولین نمونس و تنها مشکل شرط اوله که 1 کیلومتر بیشتر از اون چیزیه که میخواین، با خودتون میگید خوب 1 کیلومتر در مقابل اون شرایط خوب که چیزی نیس و این مورد آخر رو انتخاب می کنید!
منطق فازی دقیقا همینو میگه! یعنی مثل منطق باینری که کاملا سخت گیرانه شرایط رو چک میکنه عمل نمی کنه بلکه مثل مغز آدم انعطاف پذیره.
این روزا تو خیلی چیزها از منطق فازی استفاده میشه، مثلا چند تاشون که شاید جالب باشن اینان:

  • ترمز های ABS و سیستم کروز.
  • دوربین ها
  • ماشین ظرف شویی
  • آسانسور ها
  • ماشین لباس شویی
  • بازی های رایانه ای
  • شناخت الگو ها
  • سیستم های تهویه

فکر کنم تقریبا فایده ی منطق فازی جا افتاده باشه. برای شروع استفاده از منطق فازی باید یه سری مفاهیم اولیه رو یاد بگیریم.
ببینید منطق فازی در واقع یه راه ساده برای رسیدن به یه نتیجه ی قطعی هستش بر اساس ورودی های ناقص، خطادار یا مبهم! از یه سری قانون خیلی ساده هم پیروی می کنه:

کد پی‌اچ‌پی:
IF x AND y THEN z
IF a OR b THEN c

همونطور که می دونید if در زبان برنامه نویسی چیز جدیدی نیست! اما با یه مثال ساده شاید بشه فرقش رو نشون داد.
در نظر بگیرید دارید یه سیستم تهویه طراحی می کنید، توی سیستم های فازی بجای استفاده از شرط هایی مثل temprature>60C یا 30C<temprature<60C از اصطلاحات زیر استفاده می کنیم:

کد پی‌اچ‌پی:

IF temperature IS very cold THEN stop fan

IF temperature IS cold THEN turn down fan

IF temperature IS normal THEN maintain level

IF temperature IS hot THEN speed up fan

دقیقا مثل وقتی که شما توی ماشین نشستین، می بینید هوا خیلی گرمه بدون اینکه دمای دقیق توی ماشین رو بدونید کولر ماشین رو روشن می کنید و روی دمای کم میگذارید!
اگر دقت کنید هیچ ELSEای وجود نداره، چون دما می تونه هم سرد باشه هم متوسط با درجه های مختلف!
اپراتور های AND، OR و NOT که باهاشون توی منطق باینری آشنا هستیم توی منطق فازی هم وجود دارن.
قبل از تعریف این عملگر ها باید بدونیم مجموعه های فازی یا Fuzzy sets به چه معنی هستند. همونطور که گفتیم توی منطق فازی درجه ی درستی لزوما نباید 0 یا 1 باشه و یه گزاره می تونه مثلا 0.3 درست باشه.
بعد گفتیم که تو منطق فازی می تونیم از هوای گرم یا قد بلند صحبت کنیم، اما باید اول اونارو برای سیستم فازیمون تعریف کنیم! هر کدوم از این دسته ها یه مجموعه ی فازی رو تشکیل میدن.
در واقع یه مجموعه ی فازی یه جفت (A, m) هست که A یه مجموعه هست و m یه تابع با دامنه ی A و برد [0,1]. به ازای هر x عضو (A، m(x درجه ی عضویت یا درستی x رو نشون میده!
می دونم یه کلمه از چند تا جمله ی قبل نفهمیدین الان بصورت نمودار میبینیدشون و می فهمید که چیز خیلی پیچیده ای نیست!
خوب حالا که تعریف فازی ست هارو فهمیدیم میریم که اونارو توی نمودار ببینیم و عملگر هارو هم از روی شکل و با توجه به تعریفشون بررسی کنیم:
[عکس: 6.gif]
به عنوان مثال این شکل مجموعه ی فازی جوان رو نشون میده، شما وقتی از دوستتون می پرسین بنظرت علی جوونه؟
دوستتون اگه علی 17 سالش باشه میگه آره، اگه 25 سالش باشه میگه اییی، آره هنوز میشه بهش گفت جوونه، اگه 28 سالش باشه میگه خیلی جوون نیس و اگه 50 سالش باشه میگه نه!
این مجموعه ی فازی هم در واقع همین رو میگه! همونطور که میبینید قبل از 20 سال (m(B یک هست، یعنی 0 تا 20 کاملا عضو مجموعه ی جوان هست، هر چی که میریم جلوتر عضویت توی مجموعه ی جوانی کمتر شده، توی 25 سالگی درجه ی عضویت یا درستی 0.5 هست و توی 28 سالگی 0.2 و بعد از 30 سالگی 0 که یعنی از این سن به بعد اصلا جوان نیست!
بنظرم الان یکم بهتر مطلب جا افتاده باشه! حالا فرض کنید دو تا مجموعه ی فازی زیر رو داشته باشیم:
[عکس: 7.gif]
[عکس: 8.gif]
مجموعه ی اول رو در ابتدا در نظر میگیریم. تعریف NOT توی شکل بصورت زیره:
[عکس: 9.gif]
یا به عبارتی:

کد پی‌اچ‌پی:
NOT A = (1- m(A))

خوب حالا دو مجموعرو که بالاتر نمودارشون هست رو در نظر بگیرین، تعریف AND روی اون دو مجموعه بصورت زیره:
[عکس: 10.gif]
یا به عبارتی:

کد پی‌اچ‌پی:
A AND B = minimum(m(A), m(B))

OR هم قاعدتا تا الان حدس زدید به چه صورت خواهد بود:
[عکس: 11.gif]

کد پی‌اچ‌پی:
A OR B = maximum(m(A), m(B))[/list]

اینها مقدماتی بود از منطق فازی. البته اینا مفاهیم خیلی اولیه ی منطق فازی بودن، اما توی کار از همین مفاهیم خیلی ساده و ترکیبشون میشه نتایج خیلی عاقلانه ای گرفت.
ما تا اینجا فقط به پروسه ی Fuzzification پرداختیم! بعد از اینکه عملیات فازی روی سیستم انجام شد در نهایت یه جواب قطعی می خوایم. برای رسیدن به یه جواب قطعی از پروسه ی Defuzzification استفاده میشه.
منبع

منطق فازی

منطق فازی (fuzzy logic) اولین بار در پی تنظیم نظریهٔ مجموعه‌های فازی به وسیلهٔ پروفسور لطفی زاده (۱۹۶۵ م) در صحنهٔ محاسبات نو ظاهر شد.
واژهٔ fuzzy به معنای غیردقیق، ناواضح و مبهم (شناور) است.

کاربرد این بخش در علوم نرم‌افزاری را می‌توان به طور ساده این‌گونه تعریف کرد: منطق فازی از منطق ارزش‌های «صفر و یک» نرم‌افزارهای کلاسیک فراتر رفته و درگاهی جدید برای دنیای علوم نرم‌افزاری و رایانه‌ها می‌گشاید، زیرا فضای شناور و نامحدود بین اعداد صفر و یک را نیز در منطق و استدلال‌های خود به کار برده و به چالش می‌کشد. منطق فازی از فضای بین دو ارزش «برویم» یا «نرویم»، ارزش‌های جدید «شاید برویم» یا «می‌رویم اگر» یا حتی «احتمال دارد برویم» را استخراج کرده و به کار می‌گیرد. بدین ترتیب به عنوان مثال مدیر بانک پس از بررسی رایانه‌ای بیلاناقتصادی یک بازرگان می‌تواند فراتر از منطق «وام می‌دهیم» یا «وام نمی‌دهیم» رفته و بگوید: «وام می‌دهیم اگر…» یا «وام نمی‌دهیم ولی…».

مقدمه

دانش مورد نیاز برای بسیاری از مسائل مورد مطالعه به دو صورت متمایز ظاهر می‌شود:

۱. دانش عینی مثل مدل‌ها و معادلات و فرمول‌های ریاضی که از پیش تنظیم شده و برای حل و فصل مسائل معمولی فیزیک، شیمی، یا مهندسی مورد استفاده قرار می‌گیرد.
۲. دانش شخصی مثل دانستنی‌هایی که تا حدودی قابل توصیف و بیان زبان‌شناختی بوده، ولی امکان کمّی کردن آن‌ها با کمک ریاضیات سنتی معمولاً وجود ندارد. به این نوع دانش، دانش ضمنی یا دانش تلویحی (Tacit knowledge) گفته می‌شود.

از آن جا که در عمل هر دو نوع دانش مورد نیاز است منطق فازی می‌کوشد آن‌ها را به صورتی منظم، منطقی، و ریاضیاتی بایکدیگر هماهنگ گرداند.

تاریخچه

منطق فازی بیش از بیست سال پس از ۱۹۶۵ از درگاه دانشگاه‌ها به بیرون راه نیافت زیرا کمتر کسی معنای آنرا درک کرده بود. در اواسط دهه ۸۰ میلادی قرن گذشته صنعتگران ژاپنی معنا و ارزش صنعتی این علم را دریافته و منطق فازی را به کار گرفتند. اولین پروژه آنها طرح هدایت و کنترل تمام خودکار قطار زیرزمینی شهر سندای بود که توسط شرکت هیتاچی برنامه‌ریزی و ساخته شد. نتیجهٔ این طرح موفق و چشم‌گیر ژاپنی‌ها به طور ساده اینگونه خلاصه می‌شود: آغاز حرکت نامحسوس (تکان‌های ضربه‌ای) قطار، شتاب‌گرفتن نامحسوس، ترمز و ایستادن نامحسوس و صرفه جویی در مصرف برق.

از این پس منطق فازی بسیار سریع در تکنولوژی دستگاه‌های صوتی و تصویری ژاپنی‌ها راه یافت (از جمله نلرزیدن تصویر فیلم دیجیتال ضمن لرزیدن دست فیلم‌بردار). اروپایی‌ها بسیار دیر، یعنی در اواسط دههٔ ۱۹۹۰ میلادی، پس از خوابیدن موج بحث‌های علمی در رابطه با منطق فازی استفادهٔ صنعتی از آن را آغاز کردند.

ملاحظات آغازین

منطق فازی از جمله منطق‌های چندارزشی است و بر نظریهٔ مجموعه‌های فازی تکیه می‌کند. مجموعه‌های فازی، خود از تعمیم و گسترش مجموعه‌های قطعی به صورتی طبیعی حاصل می‌آیند.

مجموعه‌های قطعی

مجموعه‌های قطعی (Crisp sets) درواقع همان مجموعه‌های عادی و معمولی هستند که در ابتدای نظریهٔ کلاسیک مجموعه‌ها معرفی می‌شوند. افزودن صفت قطعی به واقع وجه تمایزی را ایجاد می‌نماید که به کمک آن می‌شود یکی از مفاهیم ابتکاری و حیاتی در منطق فازی موسوم به تابع عضویت را به آسانی در ذهن به وجود آورد.

در حالت مجموعه‌های قطعی، تابع عضویت فقط دو مقدار در برد خود دارد (در ریاضیات، برد یک تابع برابر با مجموعه تمام خروجی‌های تابع است).

آری و خیر (یک و صفر) که همان دو مقدار ممکن در منطق دوارزشی کلاسیک هستند؛ بنابراین:

{\displaystyle \mathbf {\mu } _{A}(x)=\left\{{\begin{matrix}1&{\mbox{if}}\ x\in A,\\0&{\mbox{if}}\ x\notin A.\end{matrix}}\right.}

که در اینجا {\displaystyle \mathbf {\mu } _{A}(x)} تابع عضویت عنصر x در مجموعه قطعی A است.

مجموعه‌های فازی

مجموعه‌های فازی (fuzzy sets) از تعمیم نظریهٔ کلاسیک مجموعه‌ها حاصل می‌آید که در منطق فازی کاربرد دارد.

برد تابع عضویت از {\displaystyle \{0,1\}} در مورد مجموعه‌های قطعی به بازهٔ بستهٔ {\displaystyle [0,1]} برای مجموعه‌های فازی تبدیل می‌شود.

متغیرهای زبانی

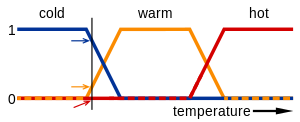منطق فازی دما

متغیرهای زبانی به متغیرهایی گفته می‌شود که مقادیر مورد قبول برای آن‌ها به جای اعداد، کلمات و جملات زبان‌های انسانی یا ماشینی هستند.
همانگونه که در محاسبات ریاضی از متغیرهای عددی استفاده می‌گردد، در منطق فازی نیز از متغیرهای زبانی (گفتاری یا غیر عددی) استفاده می‌گردد. متغیرهای زبانی بر اساس ارزش‌های زبانی (گفتاری) که در مجموعه عبارت (کلمات/اصطلاحات) قرار دارند بیان می‌شود. عبارت زبانی (Linguistic terms) صفاتی برای متغیرهای زبانی هستند. به عنوان مثال: متغیر زبانی «سن» بسته به تقسیمات مورد نظر شخصی و شرایط می‌تواند مجموعه عباراتی از قبیل «نوجوان»، «جوان»، «میان سال» و «سالمند» باشد.

مجموعه عبارات (اصطلاحات) فازی (سن) = { «جوان»، «نه جوان»، «نه چندان جوان»، «خیلی جوان» ،… ، «میان سال»، «نه چندان میان سال»… ، «پیر»، «نه پیر»، «خیلی پیر»، «کم و بیش پیر»… ، «نه خیلی جوان و نه خیلی پیر»، «نه جوان و نه پیر»…}

یا در مثالی دیگر، فشار (خون) را می‌توان متغیری زبانی در نظر گرفت، که ارزش‌هایی (خصوصیت‌هایی) از قبیل پایین، بالا، ضعیف، متوسط و قوی را می‌تواند در خود جای دهد. به زبان ریاضی داریم (T = Terms):

{پایین، بالا، ضعیف، متوسط، قوی} = (فشار)T

توابع عضویت

درجه عضویت \mu _{{A}}(x) بیانگر میزان عضویت عنصر x به مجموعه فازی {\tilde A} است. اگر درجه عضویت یک عنصر از مجموعه برابر با صفر باشد، آن عضو کاملاً از مجموعه خارج است و اگر درجه عضویت یک عضو برابر با یک باشد، آن عضو کاملاً در مجموعه قرار دارد. حال اگر درجه عضویت یک عضو مابین صفر و یک باشد، این عدد بیانگر درجه عضویت تدریجی می‌باشد.

عدم قطعیت

صفت عدم قطعیت، به صورت‌های گوناگون، در همهٔ زمینه‌ها و پدیده‌ها صرف نظر از روش شناسی مورد کاربرد جهت مطالعه، طراحی، و کنترل پدیدار می‌شود.
مفاهیم نادقیق بسیاری در پیرامون ما وجود دارند که آن‌ها را به صورت روزمره در قالب عبارت‌های مختلف بیان می‌کنیم. به عنوان مثال: «هوا خوب است» هیچ کمیتی برای خوب بودن هوا مطرح نیست تا آن را بطور دقیق اندازه‌گیری نماییم، بلکه این یک حس کیفی است. در واقع مغز انسان با در نظر گرفتن عوامل گوناگون و بر پایه تفکر استنتاجی جملات را تعریف و ارزش گذاری می‌نماید که الگوبندی آن‌ها به زبان و فرمول‌های ریاضی اگر غیرممکن نباشد، کاری بسیار پیچیده خواهد بود. منطق فازی فناوری جدیدی است که شیوه‌هایی را که برای طراحی و مدل سازی یک سیستم نیازمند ریاضیات پیچیده و پیشرفته‌است، با استفاده از مقادیر زبانی و دانش فرد خبره جایگزین می‌سازد.

انگیزه‌ها و اهداف

برای مقابلهٔ مؤثر با پیچیدگی روزافزون در بررسی، مطالعه، مدل‌سازی و حل مسائل جدید در فیزیک، مهندسی، پزشکی، زیست‌شناسی و بسیاری از امور گوناگون دیگر ایجاد و ابداع روش‌های محاسباتی جدیدی مورد نیاز شده‌است که بیشتر از پیش به شیوه‌های تفکر و تعلم خود انسان نزدیک باشد. هدف اصلی آنست که تا حد امکان، رایانه‌ها بتوانند مسائل و مشکلات بسیار پیچیدهٔ علمی را با همان سهولت و شیوایی بررسی و حل و فصل کنند که ذهن انسان قادر به ادراک و اخذ تصمیمات سریع و مناسب است.

در جهان واقعیات، بسیاری از مفاهیم را آدمی به صورت فازی (به معنای غیر دقیق، ناواضح و مبهم) درک می‌کند و به کار می‌بندد. به عنوان نمونه، هر چند کلمات و مفاهیمی همچون گرم، سرد، بلند، کوتاه، پیر، جوان و نظائر این‌ها به عدد خاص و دقیقی اشاره ندارند، اما ذهن انسان با سرعت و با انعطاف‌پذیری شگفت‌آوری همه را می‌فهمد و در تصمیمات و نتیجه‌گیریهای خود به کار می‌گیرد. این، در حالی ست که ماشین فقط اعداد را می‌فهمد و اهل دقّت است. اهداف شیوه‌های نو در علوم کامپیوتر آن است که اولاً رمز و راز این‌گونه توانایی‌ها را از انسان بیاموزد و سپس آن‌ها را تا حد امکان به ماشین یاد بدهد.

قوانین علمی گذشته در فیزیک و مکانیک نیوتونی همه بر اساس منطق قدیم استوار گردیده‌اند. در منطق قدیم فقط دو حالت داریم: سفید و سیاه، آری و خیر، روشن و تاریک، یک و صفر و درست و غلط.

متغیرها در طبیعت یا در محاسبات بر دو نوعند: ارزش‌های کمی که می‌توان با یک عدد معین بیان نمود و ارزش‌های کیفی که براساس یک ویژگی بیان می‌شود. این دو ارزش قابل تبدیل‌اند.
مثلاً در مورد قد افراد، اگر آن‌ها با ارزش عددی (سانتی‌متر) اندازه‌گیری نماییم و افراد را به دسته‌های قدکوتاه و قدبلند تقسیم‌بندی کنیم و در این دسته‌بندی، حد آستانه ۱۸۰ سانتی‌متر برای بلندی قد مدنظر باشد، در اینصورت تمامی افراد زیر ۱۸۰ سانتی‌متر براساس منطق قدیم قد کوتاه‌اند. حتی اگر قد فرد ۱۷۹ سانتی‌متر باشد؛ ولی در مجموعه فازی هر یک از این صفات براساس تابع عضویت تعریف و بین صفر تا یک ارزشگذاری می‌شود.

از آن جا که ذهن ما با منطق دیگری کارهایش را انجام می‌دهد و تصمیماتش را اتّخاذ می‌کند، جهت شروع، ایجاد و ابداع منطق‌های تازه و چندارزشی مورد نیاز است که منطق فازی یکی از آن‌ها می‌باشد.

کاربردهای صنعتی

برای هر دستور کار و خواسته عمل‌کرد مکانیکی، الکترومغناطیسی یا نرم‌افزاری و غیره که برای آن فرمول یا دستورالعمل مطلق و شفاف ریاضی وجود نداشته باشد و به‌ویژه زمانی که دستور کار به‌وسیلهٔ جملات انشاء شده باشد، نرم‌افزار متکی به منطق فازی راه‌گشا و کارآمد است.

برخی از کاربردها عبارتند از:

  • هدایت و کنترل هرگونه دستگاه و تأسیسات پویا و حرکت‌ساز را می‌توان با کمک منطق فازی به بهترین وجه اعمال نمود. از جمله ماشین لباس‌شویی، قطارها، ترمز ای‌بی‌اس خودرو،آسانسور، جرثقیل، تسمه نقاله، موتورهای احتراقی، نشست و برخاست خودکار هواپیما و غیره.
  • دستگاه‌های سمعی/بصری دیجیتال.
  • «آینده‌نگری» نرم‌افزارها جهت جلوگیری از هنگ کردن سرورها، کنترل موتورهای جستجوگر در اینترنت، سیستم‌های نرم‌افزاری ترجمه، رباتیک و هوش مصنوعی، بررسی احتمال برداشت‌هایسرندیپیتی، مهندسی پزشکی از جمله آسیب‌شناسی یا هدایت و کنترل تأسیسات سی تی اسکن، سی سی یو و آی سی یو، دستگاه ضربان‌ساز قلب.
  • کارهای ریسک شناسی، آماری و ارزیابی بانکی جهت تصمیم‌گیری‌های مدیران.
  • محاسبات آماری بیمه‌ها برای یافتن فاکتورهای ریسک در قراردادها. (بسیاری از شرکت‌های بیمه در جهان، ارزیابی صدمات و طلب خسارت مشتریان را چند سالی است بوسیله نرم‌افزارهای فازی پوشش می‌دهند و از این راه با تقلب و کلاه‌برداری‌های مشتریان مبارزه می‌کنند)

نرم‌افزارهای برای سیستم منطق فازی

  • Peach محاسبات هوشمند در پایتون
  • DotFuzzy کتابخانهٔ متن‌باز منطق فازی سی شارپ
  • JFuzzyLogic بستهٔ نرم‌افزاریِ متن باز منطق فازی برای جاوا
  • بسته pyFuzzyLib کتابخانهٔ منطق فازی در پایتون
  • بسته pyfuzzy کتابخانهٔ منطق فازی در پایتون
  • FisPro سیستم استنتاج فازی حرفه‌ای
  • (KBCT (Knowledge Base Configuration Tool ابزار پیکربندی پایگاه اطلاعات

منبع

منطق فازی (Fuzzy Logic) قسمت 1
منطق فازی (Fuzzy Logic) قسمت 2

/0 دیدگاه /توسط