از مهم‌ترین تکنیک‌های عملی داده‌کاوی که کاربرد زیادی در علوم مختلف دارد، می توان به «خوشه بندی k-میانگین» (K-means Clustering) اشاره کرد، که با توجه به بار محاسباتی زیاد آن، استفاده از کامپیوتر در انجام این فرآیند، کمک شایانی به کاربران می‌کند. در این راستا زبان برنامه‌نویسی و محاسباتی R قابلیت انجام این گونه محاسبات را دارد و به محققین در تحلیل خوشه‌بندی تفکیکی بر مبنای روش K-میانگین، کمک شایانی می‌کند. در این متن به بررسی روش خوشه‌بندی با استفاده از دستورات مربوط به این زبان برنامه‌نویسی می‌پردازیم و با البته با مفاهیم اولیه خوشه‌بندی k-میانگین نیز آشنا می‌شویم.
خوشه‌بندی k-میانگین
روش‌‌ها و الگوریتم‌های متعددی برای تبدیل اشیاء به گروه‌های همشکل یا مشابه وجود دارد. الگوریتم k-میانگین یکی از ساده‌ترین و محبوب‌ترین الگوریتم‌هایی است که در «داده‌کاوی» (Data Mining) بخصوص در حوزه «یادگیری نظارت نشده» (Unsupervised Learning) به کار می‌رود.
معمولا در حالت چند متغیره، باید از ویژگی‌های مختلف اشیا به منظور طبقه‌بندی و خوشه کردن آنها استفاده کرد. به این ترتیب با داده‌های چند بعدی سروکار داریم که معمولا به هر بعد از آن، ویژگی یا خصوصیت گفته می‌شود. با توجه به این موضوع، استفاده از توابع فاصله مختلف در این جا مطرح می‌شود. ممکن است بعضی از ویژگی‌های اشیا کمی و بعضی دیگر کیفی باشند. به هر حال آنچه اهمیت دارد روشی برای اندازه‌گیری میزان شباهت یا عدم شباهت بین اشیاء است که باید در روش‌های خوشه‌بندی لحاظ شود.
الگوریتم خوشه‌بندی k-میانگین از گروه روش‌های خوشه‌بندی تفکیکی (Partitioning Clustering) محسوب می‌شود و درجه پیچیدگی محاسباتی آن برابر با O(ndk+1) است، به شرطی که n تعداد اشیاء، d بعد ویژگی‌ها و k تعداد خوشه‌ها باشد. همچنین پیچیدگی زمانی برای این الگوریتم برابر با O(nkdi) است، که البته منظور از i تعداد تکرارهای الگوریتم برای رسیدن به جواب بهینه است.
در خوشه‌بندی k-میانگین از بهینه‌سازی یک تابع هدف (Object Function) استفاده می‌شود. پاسخ‌های حاصل از خوشه‌بندی در این روش، ممکن است به کمک کمینه‌سازی (Minimization) یا بیشینه‌سازی (Maximization) تابع هدف صورت گیرد. به این معنی که اگر ملاک «میزان فاصله» (Distance Measure) بین اشیاء باشد، تابع هدف براساس کمینه‌سازی خواهد بود پاسخ عملیات خوشه‌بندی، پیدا کردن خوشه‌هایی است که فاصله بین اشیاء هر خوشه کمینه باشد. در مقابل، اگر از تابع مشابهت (Dissimilarity Function) برای اندازه‌گیری مشابهت اشیاء استفاده شود، تابع هدف را طوری انتخاب می‌کنند که پاسخ خوشه‌بندی مقدار آن را در هر خوشه بیشینه کند.
![خوشه‌بندی k-میانگین روش‌‌ها و الگوریتم‌های متعددی برای تبدیل اشیاء به گروه‌های همشکل یا مشابه وجود دارد. الگوریتم k-میانگین یکی از ساده‌ترین و محبوب‌ترین الگوریتم‌هایی است که در «داده‌کاوی» (Data Mining) بخصوص در حوزه «یادگیری نظارت نشده» (Unsupervised Learning) به کار می‌رود. معمولا در حالت چند متغیره، باید از ویژگی‌های مختلف اشیا به منظور طبقه‌بندی و خوشه کردن آنها استفاده کرد. به این ترتیب با داده‌های چند بعدی سروکار داریم که معمولا به هر بعد از آن، ویژگی یا خصوصیت گفته می‌شود. با توجه به این موضوع، استفاده از توابع فاصله مختلف در این جا مطرح می‌شود. ممکن است بعضی از ویژگی‌های اشیا کمی و بعضی دیگر کیفی باشند. به هر حال آنچه اهمیت دارد روشی برای اندازه‌گیری میزان شباهت یا عدم شباهت بین اشیاء است که باید در روش‌های خوشه‌بندی لحاظ شود. الگوریتم خوشه‌بندی k-میانگین از گروه روش‌های خوشه‌بندی تفکیکی (Partitioning Clustering) محسوب می‌شود و درجه پیچیدگی محاسباتی آن برابر با O ( n d k + 1 ) است، به شرطی که n تعداد اشیاء، d بعد ویژگی‌ها و k تعداد خوشه‌ها باشد. همچنین پیچیدگی زمانی برای این الگوریتم برابر با O ( n k d i ) است، که البته منظور از i تعداد تکرارهای الگوریتم برای رسیدن به جواب بهینه است. در خوشه‌بندی k-میانگین از بهینه‌سازی یک تابع هدف (Object Function) استفاده می‌شود. پاسخ‌های حاصل از خوشه‌بندی در این روش، ممکن است به کمک کمینه‌سازی (Minimization) یا بیشینه‌سازی (Maximization) تابع هدف صورت گیرد. به این معنی که اگر ملاک «میزان فاصله» (Distance Measure) بین اشیاء باشد، تابع هدف براساس کمینه‌سازی خواهد بود پاسخ عملیات خوشه‌بندی، پیدا کردن خوشه‌هایی است که فاصله بین اشیاء هر خوشه کمینه باشد. در مقابل، اگر از تابع مشابهت (Dissimilarity Function) برای اندازه‌گیری مشابهت اشیاء استفاده شود، تابع هدف را طوری انتخاب می‌کنند که پاسخ خوشه‌بندی مقدار آن را در هر خوشه بیشینه کند. معمولا زمانی که هدف کمینه‌سازی باشد، تابع هدف را «تابع هزینه» (Cost Function) نیز می‌نامند. روش خوشه بندی k-میانگین، توسط «مک‌کوئین» (McQueen) جامعه شناس و ریاضیدان در سال ۱۹۶۵ ابداع و توسط دیگر دانشمندان توسعه و بهینه شد. برای مثال در سال 1957 نسخه دیگری از این الگوریتم به عنوان الگوریتم استاندارد خوشه‌بندی k-میانگین، توسط «لوید» (Lloyd) در آزمایشگاه‌های بل (Bell Labs) برای کدگذاری پالس‌ها ایجاد شد که بعدها در سال 1982 منتشر گردید. این نسخه از الگوریتم خوشه‌بندی، امروزه در بیشتر نرم‌افزارهای رایانه‌ای که عمل خوشه‌بندی k-میانگین را انجام می‌دهند به صورت استاندارد اجرا می‌شود. در سال 1956 «فورجی» (W.Forgy) به طور مستقل همین روش را ارائه کرد و به همین علت گاهی این الگوریتم را با نام لوید-فورجی می‌شناسند. همچنین روش هارتیگان- ونگ (Hartigan-Wong) که در سال ۱۹۷۹ معرفی شد یکی از روش‌هایی است که در تحقیقات و بررسی‌های داده‌کاوی مورد استفاده قرار می‌گیرد. تفاوت در این الگوریتم‌ها در مرحله آغازین و شرط همگرایی الگوریتم‌ها است ولی در بقیه مراحل و محاسبات مانند یکدیگر عمل می‌کنند. به همین علت همگی را الگوریتم‌های خوشه‌بندی k-میانگین می‌نامند. روش خوشه‌بندی k-میانگین فرض کنید مشاهدات ( x 1 , x 2 , … , x n ) که دارای d بعد هستند را باید به k بخش یا خوشه تقسیم کنیم. این بخش‌ها یا خوشه‌ها را با مجموعه‌ای به نام S = { S 1 , S 2 , … , S k } می‌شناسیم. اعضای خوشه‌ها باید به شکلی از مشاهدات انتخاب شوند که تابع «مجموع مربعات درون خوشه‌ها» (within-cluster sum of squares- WCSS) که در حالت یک بعدی شبیه واریانس است، کمینه شود. بنابراین، تابع هدف در این الگوریتم به صورت زیر نوشته می‌شود. a r g m i n S k ∑ i = 1 ∑ x ∈ S i ∥ x − μ i ∥ 2 = a r g m i n S k ∑ i = 1 | S i | Var S i در اینجا منظور از μ i میانگین خوشه S i و | S i | تعداد اعضای خوشه iام است. البته می‌توان نشان داد که کمینه کردن این مقدار به معنی بیشینه‌سازی میانگین مربعات فاصله بین نقاط در خوشه‌های مختلف (between-Cluster sum of Squares- BCSS) است زیرا طبق قانون واریانس کل، با کم شدن مقدار WCSS، مقدار BCSS افزایش می‌یابد، زیرا واریانس کل ثابت است. در ادامه به بررسی روش خوشه بندی k-میانگین به روش لوید-فورجی (استاندارد) و هارتیگان-ونگ می‌پردازیم. خوشه‌بندی k-میانگین با الگوریتم لوید (Lloyd’s Algorithm) به عنوان یک الگوریتم استاندارد برای خوشه‌بندی k-میانگین از الگوریتم لوید بخصوص در زمینه علوم کامپیوتر، استفاده می‌شود. ابتدا به علائمی که در این رابطه به کار می‌رود، اشاره می‌کنیم. m ( i ) j : میانگین مقدارهای مربوط به خوشه jام در تکرار iام از الگوریتم را با این نماد نشان می‌دهیم. S ( i ) j : مجموعه اعضای خوشه jام در تکرار iام الگوریتم. الگوریتم لوید را با توجه به نمادهای بالا می‌توان به دو بخش تفکیک کرد. ۱- بخش مقدار دهی ( A s s i g n m e n t S t e p )، ۲- بخش به روز رسانی (Update Step). حال به بررسی مراحل اجرای این الگوریتم می‌پردازیم. در اینجا فرض بر این است که نقاط مرکزی اولیه یعنی m ( 1 ) 1 , m ( 1 ) 2 , ⋯ , m ( 1 ) k داده شده‌اند. بخش مقدار دهی: هر مشاهده یا شی را به نزدیکترین خوشه نسبت می‌دهیم. به این معنی که فاصله اقلیدسی هر مشاهده از مراکز، اندازه گرفته شده سپس آن مشاهده عضو خوشه‌ای خواهد شد که کمترین فاصله اقلیدسی را با مرکز آن خوشه دارد. این قانون را به زبان ریاضی به صورت S ( t ) i = { x p : ∥ ∥ x p − m ( t ) i ∥ ∥ 2 ≤ ∥ ∥ x p − m ( t ) j ∥ ∥ 2 ∀ j , 1 ≤ j ≤ k } می‌نویسیم. بخش به روز رسانی: میانگین خوشه‌های جدید محاسبه می‌شود. در این حالت داریم: m ( t + 1 ) i = 1 | S ( t ) i | ∑ x j ∈ S ( t ) i x j توجه داشته باشید که منظور از | S ( t ) i | تعداد اعضای خوشه iام است. الگوریتم زمانی متوقف می‌شود که مقدار برچسب عضویت مشاهدات تغییری نکند. البته در چنین حالتی هیچ تضمینی برای رسیدن به جواب بهینه (با کمترین مقدار برای تابع هزینه) وجود ندارد. کاملا مشخص است که در رابطه بالا، فاصله اقلیدسی بین هر نقطه و مرکز خوشه ملاک قرار گرفته است. از این جهت از میانگین و فاصله اقلیدسی استفاده شده که مجموع فاصله اقلیدسی نقاط از میانگینشان کمترین مقدار ممکن نسبت به هر نقطه دیگر است. نکته: ممکن است فاصله اقلیدسی یک مشاهده از دو مرکز یا بیشتر، برابر باشد ولی در این حالت آن شئ فقط به یکی از این خوشه‌ها تعلق خواهد گرفت. تصویر زیر یک مثال برای همگرایی الگوریتم لوید محسوب می‌شود که مراحل اجرا در آن دیده می‌شود. همانطور که مشخص است الگوریتم با طی ۱۴ مرحله به همگرایی می‌رسد و دیگر میانگین خوشه‌ها تغییری نمی‌یابد. البته ممکن است که این نقاط نتیجه تابع هزینه را بطور کلی (Global) کمینه نکنند زیرا روش k-میانگین بهینه‌سازی محلی (Local Optimization) را به کمک مشتق‌گیری و محاسبه نقاط اکستریمم اجرا می‌کند. K-means_convergence همگرایی الگوریتم k-میانگین نکته: به نقاط مرکزی هر خوشه مرکز (Centroid) گفته می‌شود. ممکن است این نقطه یکی از مشاهدات یا غیر از آنها باشد. مشخص است که در الگوریتم لوید، k مشاهده به عنوان مرکز خوشه‌ها (Centroids) در مرحله اول انتخاب شده‌اند ولی در مراحل بعدی، مقدار میانگین هر خوشه نقش مرکز را بازی می‌کند. خوشه‌بندی k-میانگین با الگوریتم هارتیگان-ونگ (Hartigan-Wong) یکی از روش‌های پیشرفته و البته با هزینه محاسباتی زیاد در خوشه‌بندی k-میانگین، الگوریتم هارتیگان-ونگ است. برای آشنایی با این الگوریتم بهتر است ابتدا در مورد نمادهایی که در ادامه خواهید دید توضیحی ارائه شود. ϕ ( S j ) : از این نماد برای نمایش «تابع هزینه» برای خوشه S j استفاده می‌کنیم. این تابع در خوشه‌بندی k-میانگین برابر است با: ϕ ( S i ) = ∑ x ∈ S j ( x − μ j ) 2 S j : از آنجایی که هدف از این الگوریتم، تفکیک اشیاء به k گروه مختلف است، گروه‌ها یا خوشه‌ها در مجموعه‌ای با نام S قرار دارند و داریم، S = { S 1 , S 2 , ⋯ , S k } . μ j : برای نمایش میانگین خوشهjام از این نماد استفاده می‌شود. بنابراین خواهیم داشت: μ j = ∑ x ∈ S j x n j n j : این نماد تعداد اعضای خوشه jام را نشان می‌دهد. بطوری که j = { 1 , 2 , ⋯ , k } است. البته مشخص است که در اینجا تعداد خوشه‌ها را با k نشان داده‌ایم. مراحل اجرای الگوریتم در خوشه‌بندی k-میانگین با الگوریتم هارتیگان می‌توان مراحل اجرا را به سه بخش تقسیم کرد: ۱- بخش مقدار دهی اولیه ( A s s i g n m e n t S t e p ) ، ۲- بخش به روز رسانی ( U p d a t e S t e p )، ۳- بخش نهایی (Termination). در ادامه به بررسی این بخش‌ها پرداخته می‌شود. بخش مقدار دهی اولیه: در الگوریتم هارتیگان-ونگ، ابتدا مشاهدات و یا اشیاء به طور تصادفی به k گروه یا خوشه تقسیم می‌شوند. به این کار مجموعه S با اعضایی به صورت { S j } j ∈ { i , ⋯ , k } مشخص می‌شود. بخش به روز رسانی: فرض کنید که مقدارهای n و m از اعداد ۱ تا k انتخاب شده باشد. مشاهده یا شیئ از خوشه nام را در نظر بگیرید که تابع Δ ( m , n , x ) = ϕ ( S n ) + ϕ ( S m ) − Φ ( S n ∖ { x } ) − ϕ ( S m ∪ { x } ) را کمینه سازد، در چنین حالتی مقدار x از خوشه nام به خوشه mام منتقل می‌شود. به این ترتیب شی مورد نظر در S m قرار گرفته و خواهیم داشت x ∈ S m . بخش نهایی: زمانی که به ازای همه n,m,x مقدار Δ ( m , n , x ) بزرگتر از صفر باشد، الگوریتم خاتمه می‌یابد. نکته: منظور از نماد ϕ ( S n ∖ { x } ) محاسبه تابع هزینه در زمانی است که مشاهده x از مجموعه S n خارج شده باشد. همچنین نماد ϕ ( S m ∪ { x } ) به معنی محاسبه تابع هزینه در زمانی است که مشاهده x به خوشه S m اضافه شده باشد. در تصویر زیر مراحل اجرای الگوریتم هارتیگان به خوبی نمایش داده شده است. هر تصویر بیانگر یک مرحله از اجرای الگوریتم است. نقاط رنگی نمایش داده شده، همان مشاهدات هستند. هر رنگ نیز بیانگر یک خوشه است. در تصویر اول مشخص است که در بخش اول از الگوریتم به طور تصادفی خوشه‌بندی صورت پذیرفته. ولی در مراحل بعدی خوشه‌ها اصلاح شده و در انتها به نظر می‌رسد که بهترین تفکیک برای مشاهدات رسیده‌ایم. در تصویر آخر نیز مشخص است که مراکز خوشه‌ها، محاسبه و ثابت شده و دیگر بهینه‌سازی صورت نخواهد گرفت. به این ترتیب پاسخ‌های الگوریتم با طی تکرار ۵ مرحله به همگرایی می‌رسد. hartigan algorithm الگوریتم هارتیگان بخش مقدار دهی اولیه hartigan algorithm الگوریتم هارتیگان تکرار ۱ hartigan algorithm الگوریتم هارتیگان تکرار ۲ hartigan algorithm الگوریتم هارتیگان تکرار ۳ hartigan algorithm الگوریتم هارتیگان تکرار ۴ hartigan algorithm الگورییتم هارتیگان تکرار ۵ اجرای این الگوریتم‌ها با استفاده از دستورات زبان برنامه‌نویسی R برای استفاده از دستورات و فرمان‌های مربوط به خوشه‌بندی k-میانگین، باید بسته یا Package مربوط به خوشه‌بندی kmeans به اسم stats را در R نصب کرده باشد. البته از آنجایی این بسته بسیار پرکاربرد است، معمولا به طور خودکار فراخوانی شده است. کدهای زیر نشانگر استفاده از الگوریتم خوشه‌بندی توسط روش‌های مختلف آن است. library(stats) data=iris[,1:4] method=c("Hartigan-Wong", "Lloyd", "MacQueen") k=3 kresults1=kmeans(data,k,algorithm = method[1]) kresults2=kmeans(data,k,algorithm=method[2]) kresults3=kmeans(data,k,algorithm=method[3]) kresults1 kresults2 kresults3 1 2 3 4 5 6 7 8 9 10 11 12 library(stats) data=iris[,1:4] method=c("Hartigan-Wong", "Lloyd", "MacQueen") k=3 kresults1=kmeans(data,k,algorithm = method[1]) kresults2=kmeans(data,k,algorithm=method[2]) kresults3=kmeans(data,k,algorithm=method[3]) kresults1 kresults2 kresults3 با توجه به داده‌های iris که مربوط به اندازه و ابعاد کاسبرگ و گلبرگ سه نوع گل مختلف است، خوشه‌بندی به سه دسته انجام شده است. اطلاعات مربوط به ۱۰ سطر اول این مجموعه داده، به صورت زیر است. با اجرای کدهای نوشته شده، خوشه‌بندی انجام شده و نتابج تولید می‌شوند. به عنوان مثال می‌توان خروجی را برای kresult1 که انجام خوشه بندی توسط الگوریتم هارتیگان است به صورت زیر مشاهده کرد: iris clustering همانطور که دیده می‌شود، در سطر اول تعداد اعضای هر خوشه، نمایش داده شده است. در بخش دوم که با سطر ۱ و ۲ و ۳ مشخص شده، مراکز هر سه خوشه برحسب ویژگی‌های (طول و عرض کاسبرگ و طول و عرض گلبرگ) محاسبه شده و در قسمت Cluster Vector نیز برچسب خوشه هر کدام از مشاهدات دیده می‌شود. در انتها نیز مجموع مربعات فاصله درون خوشه‌ای (مجموع فاصله هر مشاهده از مرکز خوشه) استخراج شده و درصد یا شاخص ارزیابی خوشه‌بندی بر اساس نسبت مربعات بین خوشه‌ها به مربعات کل دیده می‌شود. این مقدار برای این حالت برابر ۸۸.۴٪ است که نشان می‌دهد بیشتر پراکندگی (total_ss) توسط پراکندگی بین خوشه‌ها (between_ss) بیان شده است. پس به نظر خوشه‌بندی مناسب خواهد بود. پس اختلاف بین گروه‌ها ناشی از خوشه‌های است که مشاهدات را به دسته‌‌های جداگانه تفکیک کرده. همچنین در کدها مشخص است که تعداد خوشه‌های در متغیر k ثبت و به کار رفته است. در شکل دیگری از دستور kmeans می‌توان به جای معرفی تعداد خوشه‌ها از مراکز دلخواه که با تعداد خوشه‌ها مطابقت دارد، استفاده کرد. برای مثال اگر برنامه به صورت زیر نوشته شود، الگوریتم ابتدا نقاط معرفی شده را به عنوان نقاط مرکزی (Centroids) به کار گرفته و سپس مراحل بهینه سازی را دنبال می‌کند. از آنجا که سه نقطه مبنا قرار گرفته، الگوریتم متوجه می‌شود که باید مشاهدات به سه خوشه تفکیک شود. library(stats) data=iris[,1:4] method=c("Hartigan-Wong", "Lloyd", "MacQueen") c1=c(6,4,5,3) c2=c(5,3,1,0) c3=c(6,2,4,2) centers=rbind(c1,c2,c3) kresults1=kmeans(x = data,centers = centers,algorithm = method[1]) kresults2=kmeans(x = data,centers = centers,algorithm=method[2]) kresults3=kmeans(x = data,centers = centers,algorithm=method[3]) kresults1 kresults2 kresults3 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 library(stats) data=iris[,1:4] method=c("Hartigan-Wong", "Lloyd", "MacQueen") c1=c(6,4,5,3) c2=c(5,3,1,0) c3=c(6,2,4,2) centers=rbind(c1,c2,c3) kresults1=kmeans(x = data,centers = centers,algorithm = method[1]) kresults2=kmeans(x = data,centers = centers,algorithm=method[2]) kresults3=kmeans(x = data,centers = centers,algorithm=method[3]) kresults1 kresults2 kresults3 در تصویر زیر نتیجه خوشه بندی k-میانگین را برای داده‌های iris توسط یک نمودار مشاهده می‌کنید. البته باید توجه داشت که این نمودار دو بعدی است در حالیکه داده‌ها، دارای چهار ویژگی هستند. به کمک روش‌های آماری مانند تجزیه به مولفه‌های اصلی (PCA) ابعاد مسئله کاهش یافته تا در سه بعد روی نمودار نمایش داده شود. سمت راست تصویر گروه‌های واقعی و سمت چپ نتیجه خوشه‌بندی دیده می‌شود. نقاطی که در خوشه‌ها به درستی تشخیص داده نشده‌اند، باعث افزایش خطای خوشه‌بندی خواهند شد. کاربردها از الگوریتم خوشه‌بندی k-میانگین در «بخش‌بندی بازار کسب و کار» (market Segmentation)، «دسته‌بندی مشتریان» (Customer Segmentation)، «بینایی رایانه‌ای» (Computer Vision) و «زمین‌آمار (Geostatistics) استفاده می شود. برای مثال در تشخیص تعداد رنگ و یا فشرده سازی تصاویر برحسب رنگ‌ها می‌توان از این الگوریتم‌ها استفاده کرد. در تصویر بالا گل رز زرد رنگی دیده می‌شود که در یک محیط سبز قرار گرفته است. با استفاده از الگوریتم‌های خوشه‌بندی می‌توان تعداد رنگ‌ها را کاهش داده و از حجم تصاویر کاست. در تصویر زیر دسته بندی رنگ‌های گل رز دیده می‌شود. در این تصویر، هر طیف رنگ براساس میزان رنگ قرمز و سبز، بوسیله «سلول‌های ورونوی» (Voronoi Cell) تقسیم‌بندی شده است. این تقسیم‌بندی می‌تواند توسط الگوریتم‌ها خوشه‌بندی k-میانگین صورت گرفته باشد. در کل تصویر نیز، طیف رنگ‌های مختلف برای تصویر گل رز در یک «نمودار ورونوی» (Voronoi diagram) نمایش داده شده است که خوشه‌ها را بیان می‌کند. معایب و مزایای خوشه‌بندی k-میانگین از آنجایی که در این روش خوشه‌بندی، محاسبه فاصله بین نقاط توسط تابع فاصله اقلیدسی انجام می‌شود، از این الگوریتم‌ها به صورت استاندارد، فقط برای مقدارهای عددی (و نه ویژگی‌های کیفی) می‌توان استفاده کرد. از طرف دیگر با توجه به محاسبات ساده و سریع آنها، پرکاربرد و موثر است. از طرف دیگر نسخه‌های تعمیم یافته از روش خوشه بندی k-میانگین نیز وجود دارد که با توابع فاصله دیگر مانند فاصله منهتن و یا فاصله‌هایی که برای داده‌های باینری قابل استفاده است، مراحل خوشه‌بندی را انجام می‌دهد. به منظور ارزیابی نتایج خوشه‌بندی از معیارهای متفاوتی کمک گرفته می‌شود. ممکن است از قبل برچسب خوشه‌ها مشخص باشد و بخواهیم کارایی الگوریتم را با توجه به مقایسه برچسب‌های واقعی و حاصل از خوشه‌بندی، اندازه‌گیری کنیم. در این حالت، شاخص‌های ارزیابی بیرونی، بهترین راهنما و معیار برای سنجش صحت نتایج خوشه‌بندی محسوب می‌شوند. معمولا به این برچسب‌ها، استاندارد طلایی (Golden Standard) و در کل چنین عملی را ارزیابی Benchmark می‌گویند. برای مثال شاخص رَند (Rand Index) یکی از این معیارها و شاخص‌های بیرونی است که از محبوبیت خاصی نیز برخوردار است. از طرف دیگر اگر هیچ اطلاعات اولیه از ساختار و دسته‌بندی مشاهدات وجود نداشته باشد، فقط ملاک ارزیابی، می‌تواند اندازه‌هایی باشد که میزان شباهت درون خوشه‌ها و یا عدم شباهت یا فاصله بین خوشه‌ها را اندازه می‌گیرند. بنابراین برای انتخاب بهتر و موثرترین روش خوشه‌بندی از میزان شباهت درون خوشه‌ها و شباهت بین خوشه‌ها استفاده می‌شود. روشی که دارای میزان شباهت بین خوشه‌ای کم و شباهت درون خوشه‌ای زیاد باشد مناسب‌ترین روش خواهد بود. این معیارها را به نام شاخص‌های ارزیابی درونی می‌شناسیم. به عنوان مثال شاخص نیم‌رخ (silhouette) یکی از این معیارها است که شاخصی برای سنجش مناسب بودن تعلق هر مشاهده به خوشه‌اش ارائه می‌دهد. به این ترتیب معیاری برای اندازه‌گیری کارایی الگوریتم خوشه‌بندی بدست می‌آید. اگر این مطلب برایتان مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند: مجموعه آموزش‌های یادگیری ماشین و بازشناسی الگو مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی آموزش خوشه بندی K میانگین (K-Means) با نرم افزار SPSS آموزش خوشه بندی تفکیکی با نرم افزار R آموزش خوشه بندی سلسله مراتبی با SPSS آشنایی با خوشه‌بندی (Clustering) و شیوه‌های مختلف آن روش های ارزیابی نتایج خوشه بندی (Clustering Performance) — معیارهای درونی (Internal Index) روش های ارزیابی نتایج خوشه بندی (Clustering Performance) — معیارهای بیرونی (External Index) ^^ telegram twitter به اشتراک بگذارید: منبع وبلاگ فرادرسWikipedia بر اساس رای 1 نفر آیا این مطلب برای شما مفید بود؟ بلیخیر نظر شما چیست؟ نشانی ایمیل شما منتشر نخواهد شد. بخش‌های موردنیاز علامت‌گذاری شده‌اند * متن نظر * نام شما * ایمیل شما * پایتخت ایران کدام شهر است؟ برچسب‌ها clusterClusteringclustering algorithmcost functiondata miningforgy algorithmhartigan-wong algorithmk-meanslloyd algorithmmaximizationMcQueen algorithmminimizationpartitioning algorithmunsupervise learningتابع هدفتابع هزینهتعداد خوشهخوشه بندیخوشه بندی K میانگینخوشه بندی در آمارخوشه‌بندیخوشه‌بندی k-میانگینمربعات بین خوشهمربعات درون خوشهمعیارهای ارزیابی خوشه عضویت در خبرنامه ایمیل * آموزش برنامه نویسی آموزش متلب Matlab نرم‌افزارهای مهندسی برق نرم‌افزارهای مهندسی عمران نرم‌افزارهای مهندسی مکانیک نرم‌افزارهای مهندسی صنایع](https://blog.faradars.org/wp-content/uploads/2018/10/kmeans.jpg)
معمولا زمانی که هدف کمینه‌سازی باشد، تابع هدف را «تابع هزینه» (Cost Function) نیز می‌نامند.
روش خوشه بندی k-میانگین، توسط «مک‌کوئین» (McQueen) جامعه شناس و ریاضیدان در سال ۱۹۶۵ ابداع و توسط دیگر دانشمندان توسعه و بهینه شد. برای مثال در سال 1957 نسخه دیگری از این الگوریتم به عنوان الگوریتم استاندارد خوشه‌بندی k-میانگین، توسط «لوید» (Lloyd) در آزمایشگاه‌های بل (Bell Labs) برای کدگذاری پالس‌ها ایجاد شد که بعدها در سال 1982 منتشر گردید. این نسخه از الگوریتم خوشه‌بندی، امروزه در بیشتر نرم‌افزارهای رایانه‌ای که عمل خوشه‌بندی k-میانگین را انجام می‌دهند به صورت استاندارد اجرا می‌شود. در سال 1956 «فورجی» (W.Forgy) به طور مستقل همین روش را ارائه کرد و به همین علت گاهی این الگوریتم را با نام لوید-فورجی می‌شناسند. همچنین روش هارتیگان- ونگ (Hartigan-Wong) که در سال ۱۹۷۹ معرفی شد یکی از روش‌هایی است که در تحقیقات و بررسی‌های داده‌کاوی مورد استفاده قرار می‌گیرد. تفاوت در این الگوریتم‌ها در مرحله آغازین و شرط همگرایی الگوریتم‌ها است ولی در بقیه مراحل و محاسبات مانند یکدیگر عمل می‌کنند. به همین علت همگی را الگوریتم‌های خوشه‌بندی k-میانگین می‌نامند.
روش خوشه‌بندی k-میانگین
فرض کنید مشاهدات که دارای d بعد هستند را باید به k بخش یا خوشه تقسیم کنیم. این بخش‌ها یا خوشه‌ها را با مجموعه‌ای به نام می‌شناسیم. اعضای خوشه‌ها باید به شکلی از مشاهدات انتخاب شوند که تابع «مجموع مربعات درون خوشه‌ها» (within-cluster sum of squares- WCSS) که در حالت یک بعدی شبیه واریانس است، کمینه شود.
بنابراین، تابع هدف در این الگوریتم به صورت زیر نوشته می‌شود.
در اینجا منظور از میانگین خوشه و تعداد اعضای خوشه iام است. البته می‌توان نشان داد که کمینه کردن این مقدار به معنی بیشینه‌سازی میانگین مربعات فاصله بین نقاط در خوشه‌های مختلف (between-Cluster sum of Squares- BCSS) است زیرا طبق قانون واریانس کل، با کم شدن مقدار WCSS، مقدار BCSS افزایش می‌یابد، زیرا واریانس کل ثابت است.
در ادامه به بررسی روش خوشه بندی k-میانگین به روش لوید-فورجی (استاندارد) و هارتیگان-ونگ می‌پردازیم.
خوشه‌بندی k-میانگین با الگوریتم لوید (Lloyd’s Algorithm)
به عنوان یک الگوریتم استاندارد برای خوشه‌بندی k-میانگین از الگوریتم لوید بخصوص در زمینه علوم کامپیوتر، استفاده می‌شود. ابتدا به علائمی که در این رابطه به کار می‌رود، اشاره می‌کنیم.
mj(i): میانگین مقدارهای مربوط به خوشه jام در تکرار iام از الگوریتم را با این نماد نشان می‌دهیم.
Sj(i): مجموعه اعضای خوشه jام در تکرار iام الگوریتم.
الگوریتم لوید را با توجه به نمادهای بالا می‌توان به دو بخش تفکیک کرد. ۱- بخش مقدار دهی ()، ۲- بخش به روز رسانی (Update Step). حال به بررسی مراحل اجرای این الگوریتم می‌پردازیم. در اینجا فرض بر این است که نقاط مرکزی اولیه یعنی داده شده‌اند.
- بخش مقدار دهی: هر مشاهده یا شی را به نزدیکترین خوشه نسبت می‌دهیم. به این معنی که فاصله اقلیدسی هر مشاهده از مراکز، اندازه گرفته شده سپس آن مشاهده عضو خوشه‌ای خواهد شد که کمترین فاصله اقلیدسی را با مرکز آن خوشه دارد. این قانون را به زبان ریاضی به صورت
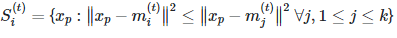می‌نویسیم. - بخش به روز رسانی: میانگین خوشه‌های جدید محاسبه می‌شود. در این حالت داریم:
توجه داشته باشید که منظور از Si(t| تعداد اعضای خوشه iام است. الگوریتم زمانی متوقف می‌شود که مقدار برچسب عضویت مشاهدات تغییری نکند. البته در چنین حالتی هیچ تضمینی برای رسیدن به جواب بهینه (با کمترین مقدار برای تابع هزینه) وجود ندارد. کاملا مشخص است که در رابطه بالا، فاصله اقلیدسی بین هر نقطه و مرکز خوشه ملاک قرار گرفته است. از این جهت از میانگین و فاصله اقلیدسی استفاده شده که مجموع فاصله اقلیدسی نقاط از میانگینشان کمترین مقدار ممکن نسبت به هر نقطه دیگر است.
نکته: ممکن است فاصله اقلیدسی یک مشاهده از دو مرکز یا بیشتر، برابر باشد ولی در این حالت آن شئ فقط به یکی از این خوشه‌ها تعلق خواهد گرفت.
تصویر زیر یک مثال برای همگرایی الگوریتم لوید محسوب می‌شود که مراحل اجرا در آن دیده می‌شود. همانطور که مشخص است الگوریتم با طی ۱۴ مرحله به همگرایی می‌رسد و دیگر میانگین خوشه‌ها تغییری نمی‌یابد. البته ممکن است که این نقاط نتیجه تابع هزینه را بطور کلی (Global) کمینه نکنند زیرا روش k-میانگین بهینه‌سازی محلی (Local Optimization) را به کمک مشتق‌گیری و محاسبه نقاط اکستریمم اجرا می‌کند.
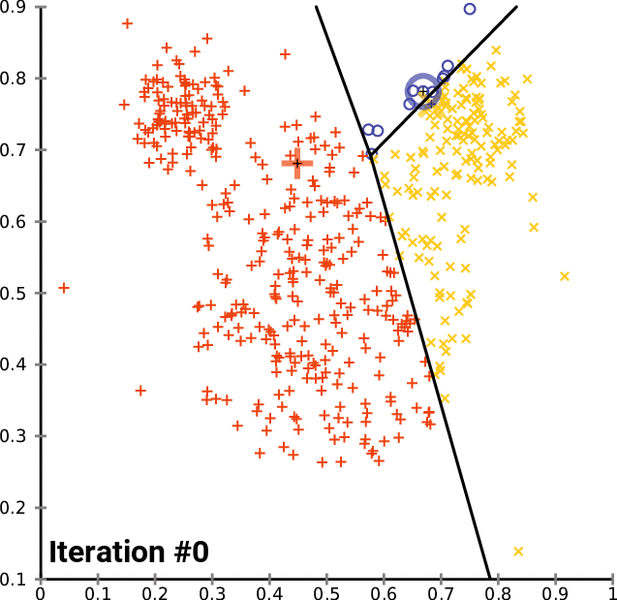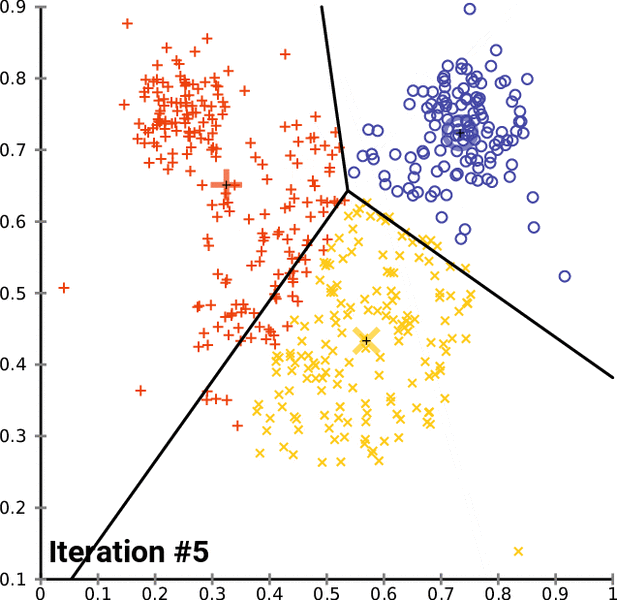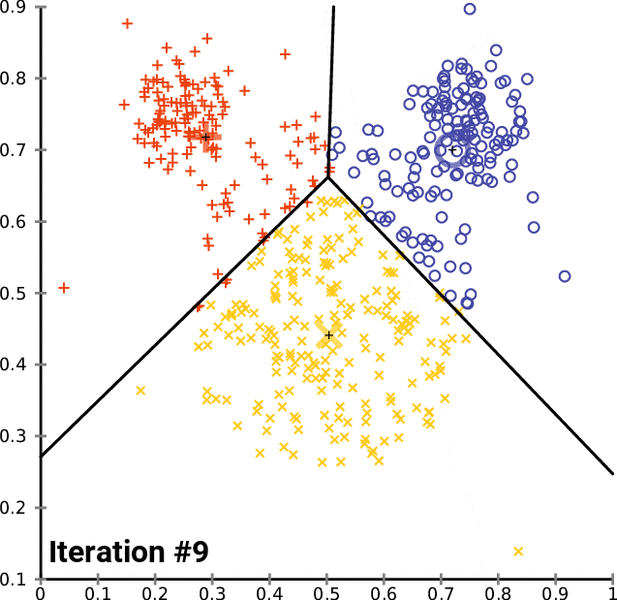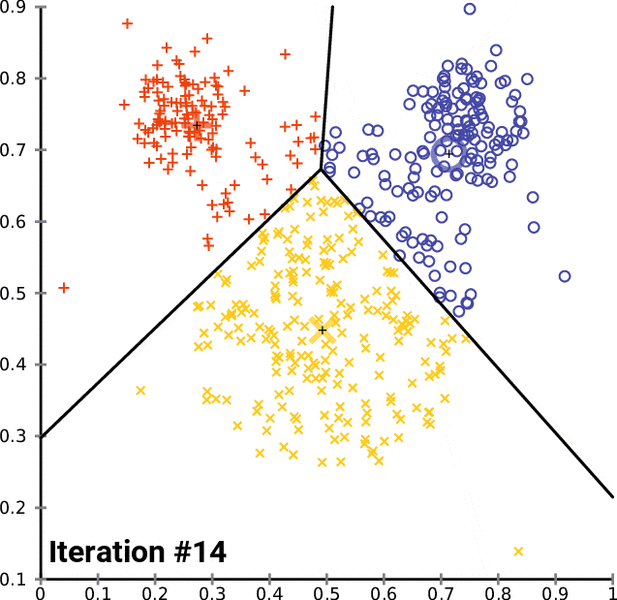
همگرایی الگوریتم k-میانگین
نکته: به نقاط مرکزی هر خوشه مرکز (Centroid) گفته می‌شود. ممکن است این نقطه یکی از مشاهدات یا غیر از آنها باشد. مشخص است که در الگوریتم لوید، k مشاهده به عنوان مرکز خوشه‌ها (Centroids) در مرحله اول انتخاب شده‌اند ولی در مراحل بعدی، مقدار میانگین هر خوشه نقش مرکز را بازی می‌کند.
خوشه‌بندی k-میانگین با الگوریتم هارتیگان-ونگ (Hartigan-Wong)
یکی از روش‌های پیشرفته و البته با هزینه محاسباتی زیاد در خوشه‌بندی k-میانگین، الگوریتم هارتیگان-ونگ است. برای آشنایی با این الگوریتم بهتر است ابتدا در مورد نمادهایی که در ادامه خواهید دید توضیحی ارائه شود.
از این نماد برای نمایش «تابع هزینه» برای خوشه 
استفاده می‌کنیم. این تابع در خوشه‌بندی k-میانگین برابر است با:
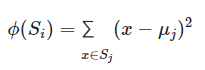
: از آنجایی که هدف از این الگوریتم، تفکیک اشیاء به k گروه مختلف است، گروه‌ها یا خوشه‌ها در مجموعه‌ای با نام S قرار دارند و داریم، 
: برای نمایش میانگین خوشهjام از این نماد استفاده می‌شود. بنابراین خواهیم داشت:
این نماد تعداد اعضای خوشه jام را نشان می‌دهد. بطوری که 
است. البته مشخص است که در اینجا تعداد خوشه‌ها را با k نشان داده‌ایم.
مراحل اجرای الگوریتم
در خوشه‌بندی k-میانگین با الگوریتم هارتیگان می‌توان مراحل اجرا را به سه بخش تقسیم کرد: ۱- بخش مقدار دهی اولیه (Assignment Step( ،- ۲ بخش به روز رسانی (Update Step)، ۳- بخش نهایی (Termination). در ادامه به بررسی این بخش‌ها پرداخته می‌شود.
- بخش مقدار دهی اولیه: در الگوریتم هارتیگان-ونگ، ابتدا مشاهدات و یا اشیاء به طور تصادفی به k گروه یا خوشه تقسیم می‌شوند. به این کار مجموعه S با اعضایی به صورت
مشخص می‌شود. - بخش به روز رسانی: فرض کنید که مقدارهای n و m از اعداد ۱ تا k انتخاب شده باشد. مشاهده یا شیئ از خوشه nام را در نظر بگیرید که تابع
را کمینه سازد، در چنین حالتی مقدار x از خوشه nام به خوشه mام منتقل می‌شود. به این ترتیب شی مورد نظر در 
قرار گرفته و خواهیم داشت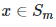 
. - بخش نهایی: زمانی که به ازای همه n,m,x مقدار
بزرگتر از صفر باشد، الگوریتم خاتمه می‌یابد.
نکته: منظور از نماد 
محاسبه تابع هزینه در زمانی است که مشاهده x از مجموعه 
خارج شده باشد. همچنین نماد 
به معنی محاسبه تابع هزینه در زمانی است که مشاهده x به خوشه اضافه شده باشد.
در تصویر زیر مراحل اجرای الگوریتم هارتیگان به خوبی نمایش داده شده است. هر تصویر بیانگر یک مرحله از اجرای الگوریتم است. نقاط رنگی نمایش داده شده، همان مشاهدات هستند. هر رنگ نیز بیانگر یک خوشه است.
در تصویر اول مشخص است که در بخش اول از الگوریتم به طور تصادفی خوشه‌بندی صورت پذیرفته. ولی در مراحل بعدی خوشه‌ها اصلاح شده و در انتها به نظر می‌رسد که بهترین تفکیک برای مشاهدات رسیده‌ایم.
در تصویر آخر نیز مشخص است که مراکز خوشه‌ها، محاسبه و ثابت شده و دیگر بهینه‌سازی صورت نخواهد گرفت. به این ترتیب پاسخ‌های الگوریتم با طی تکرار ۵ مرحله به همگرایی می‌رسد.
الگوریتم هارتیگان بخش مقدار دهی اولیه
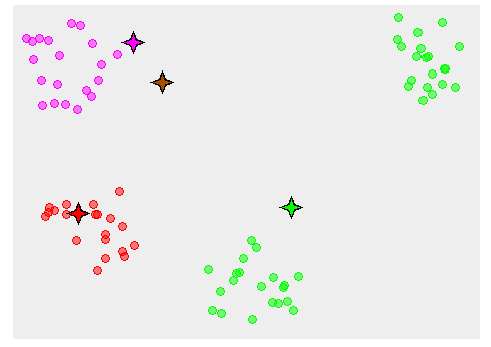
الگوریتم هارتیگان تکرار 1
الگوریتم هارتیگان تکرار 2
الگوریتم هارتیگان تکرار 3
الگوریتم هارتیگان تکرار 4
الگوریتم هارتیگان تکرار 5
اجرای این الگوریتم‌ها با استفاده از دستورات زبان برنامه‌نویسی R
برای استفاده از دستورات و فرمان‌های مربوط به خوشه‌بندی k-میانگین، باید بسته یا Package مربوط به خوشه‌بندی kmeans به اسم stats را در R نصب کرده باشد. البته از آنجایی این بسته بسیار پرکاربرد است، معمولا به طور خودکار فراخوانی شده است. کدهای زیر نشانگر استفاده از الگوریتم خوشه‌بندی توسط روش‌های مختلف آن است.
library(stats) data=iris[,1:4] method=c("Hartigan-Wong", "Lloyd", "MacQueen") k=3 kresults1=kmeans(data,k,algorithm = method[1]) kresults2=kmeans(data,k,algorithm=method[2]) kresults3=kmeans(data,k,algorithm=method[3]) kresults1 kresults2 kresults3
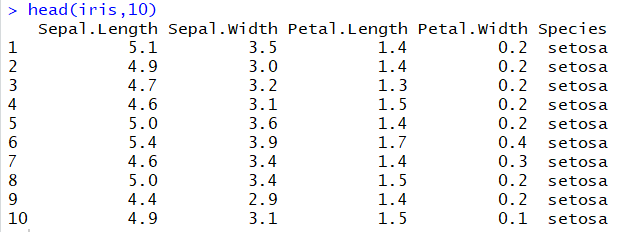
با اجرای کدهای نوشته شده، خوشه‌بندی انجام شده و نتابج تولید می‌شوند. به عنوان مثال می‌توان خروجی را برای kresult1 که انجام خوشه بندی توسط الگوریتم هارتیگان است به صورت زیر مشاهده کرد:
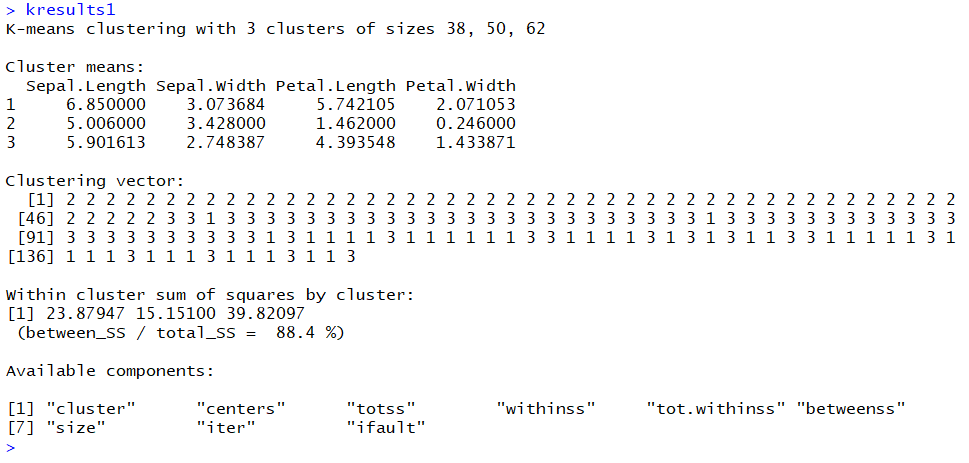
همانطور که دیده می‌شود، در سطر اول تعداد اعضای هر خوشه، نمایش داده شده است. در بخش دوم که با سطر ۱ و ۲ و ۳ مشخص شده، مراکز هر سه خوشه برحسب ویژگی‌های (طول و عرض کاسبرگ و طول و عرض گلبرگ) محاسبه شده و در قسمت Cluster Vector نیز برچسب خوشه هر کدام از مشاهدات دیده می‌شود. در انتها نیز مجموع مربعات فاصله درون خوشه‌ای (مجموع فاصله هر مشاهده از مرکز خوشه) استخراج شده و درصد یا شاخص ارزیابی خوشه‌بندی بر اساس نسبت مربعات بین خوشه‌ها به مربعات کل دیده می‌شود. این مقدار برای این حالت برابر ۸۸.۴٪ است که نشان می‌دهد بیشتر پراکندگی (total_ss) توسط پراکندگی بین خوشه‌ها (between_ss) بیان شده است. پس به نظر خوشه‌بندی مناسب خواهد بود. پس اختلاف بین گروه‌ها ناشی از خوشه‌های است که مشاهدات را به دسته‌‌های جداگانه تفکیک کرده.
همچنین در کدها مشخص است که تعداد خوشه‌های در متغیر k ثبت و به کار رفته است. در شکل دیگری از دستور kmeans می‌توان به جای معرفی تعداد خوشه‌ها از مراکز دلخواه که با تعداد خوشه‌ها مطابقت دارد، استفاده کرد. برای مثال اگر برنامه به صورت زیر نوشته شود، الگوریتم ابتدا نقاط معرفی شده را به عنوان نقاط مرکزی (Centroids) به کار گرفته و سپس مراحل بهینه سازی را دنبال می‌کند. از آنجا که سه نقطه مبنا قرار گرفته، الگوریتم متوجه می‌شود که باید مشاهدات به سه خوشه تفکیک شود.
library(stats)
data=iris[,1:4]
method=c("Hartigan-Wong", "Lloyd",
"MacQueen")
c1=c(6,4,5,3)
c2=c(5,3,1,0)
c3=c(6,2,4,2)
centers=rbind(c1,c2,c3)
kresults1=kmeans(x = data,centers = centers,algorithm = method[1])
kresults2=kmeans(x = data,centers = centers,algorithm=method[2])
kresults3=kmeans(x = data,centers = centers,algorithm=method[3])
kresults1
kresults2
kresults3
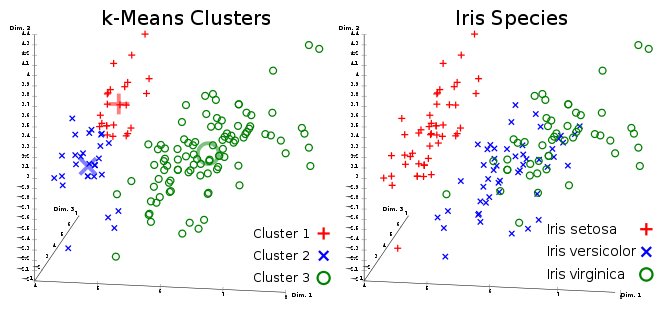
کاربردها
از الگوریتم خوشه‌بندی k-میانگین در «بخش‌بندی بازار کسب و کار» (market Segmentation)، «دسته‌بندی مشتریان» (Customer Segmentation)، «بینایی رایانه‌ای» (Computer Vision) و «زمین‌آمار (Geostatistics) استفاده می شود. برای مثال در تشخیص تعداد رنگ و یا فشرده سازی تصاویر برحسب رنگ‌ها می‌توان از این الگوریتم‌ها استفاده کرد.
در تصویر بالا گل رز زرد رنگی دیده می‌شود که در یک محیط سبز قرار گرفته است. با استفاده از الگوریتم‌های خوشه‌بندی می‌توان تعداد رنگ‌ها را کاهش داده و از حجم تصاویر کاست. در تصویر زیر دسته بندی رنگ‌های گل رز دیده می‌شود.
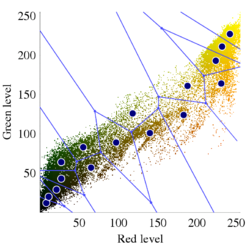
در این تصویر، هر طیف رنگ براساس میزان رنگ قرمز و سبز، بوسیله «سلول‌های ورونوی» (Voronoi Cell) تقسیم‌بندی شده است. این تقسیم‌بندی می‌تواند توسط الگوریتم‌ها خوشه‌بندی k-میانگین صورت گرفته باشد. در کل تصویر نیز، طیف رنگ‌های مختلف برای تصویر گل رز در یک «نمودار ورونوی» (Voronoi diagram) نمایش داده شده است که خوشه‌ها را بیان می‌کند.
خوشه بندی k میانگین (k-means Clustering) قسمت 1
خوشه بندی k میانگین (k-means Clustering) قسمت 2
