بهینهسازی ازدحام ذرات (PSO) قسمت 1
روش بهینهسازی ازدحام ذرات
انواع الگوریتم ازدحام ذرات
الگوریتم ازدحام ذرات پیوسته
مقدمه
الگوریتم PSO یک الگوریتم جستجوی جمعی است که از روی رفتار اجتماعی دستههای پرندگان مدل شدهاست. در ابتدا این الگوریتم به منظور کشف الگوهای حاکم بر پرواز همزمان پرندگان و تغییر ناگهانی مسیر آنها و تغییر شکل بهینهٔ دسته به کار گرفته شد. در PSO، ذرات در فضای جستجو جاری میشوند. تغییر مکان ذرات در فضای جستجو تحت تأثیر تجربه و دانش خودشان و همسایگانشان است؛ بنابراین موقعیت دیگر توده ذرات روی چگونگی جستجوی یک ذره اثر میگذارد. نتیجهٔ مدلسازی این رفتار اجتماعی فرایند جستجویی است که ذرات به سمت نواحی موفق میل میکنند. ذرات از یکدیگر میآموزند و بر مبنای دانش بدست آمده به سمت بهترین همسایگان خود میروند اساس کار PSO بر این اصل استوار است که در هر لحظه هر ذره مکان خود را در فضای جستجو با توجه به بهترین مکانی که تاکنون در آن قرار گرفتهاست و بهترین مکانی که در کل همسایگیاش وجود دارد، تنظیم میکند.
در ادامه کمی به توضیح مفهوم هوش جمعی میپردازیم.
هوش جمعی
هوش جمعی خاصیتی است سیستماتیک که در این سیستم، عاملها بهطور محلی با هم همکاری مینمایند و رفتار جمعی تمام عاملها باعث یک همگرایی در نقطهای نزدیک به جواب بهینه سراسری میشود نقطه قوت این الگوریتمها عدم نیاز آنها به یک کنترل سراسری میباشد. هر ذره) عامل) در این الگوریتمها خود مختاری نسبی دارد که میتواند در سراسر فضای جوابها حرکت کند و میبایست با سایر ذرات (عاملها) همکاری داشته باشد. دو الگوریتم مشهور هوش جمعی، بهینهسازی لانه مورچگان و بهینهسازی توده ذرات میباشند. از هر دو این الگوریتمها میتوان برای تعلیم شبکههای عصبی بهره برد.
اولین الگوریتم ازدحام ذرات
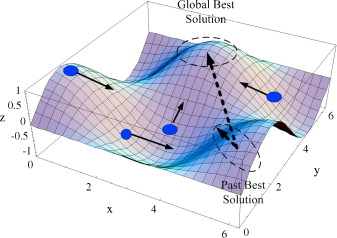
در سال ۱۹۹۵ ابرهارت و کندی برای اولین بار PSO به عنوان یک روش جستجوی غیر قطعی برای بهینهسازی تابعی مطرح گشت این الگوریتم از حرکت دسته جمعی پرندگانی که به دنبال غذا میباشند، الهام گرفته شدهاست. گروهی از پرندگان در فضایی به صورت تصادفی دنبال غذا میگردند. تنها یک تکه غذا در فضای مورد جستجو وجود دارد. هر راه حل که به آن یک ذره گفته میشود، PSO در الگوریتم معادل یک پرنده در الگوریتم حرکت جمعی پرندگان میباشد. هر ذره یک مقدار شایستگی دارد که توسط یک تابع شایستگی محاسبه میشود. هر چه ذره در فضای جستجو به هدف (غذا در مدل حرکت پرندگان) نزدیکتر باشد، شایستگی بیشتری دارد. همچنین هر ذره دارای یک سرعت است که هدایت حرکت ذره را بر عهده دارد. هر ذره با دنبال کردن ذرات بهینه در حالت فعلی، به حرکت خود در فضای مسئله ادامه میدهد.
به ا ین شکل است که گروهٔ از ذرات در آغاز کار به صورت تصادفی به وجود میآیند و با به روز کردن نسلها سعی در یافتن راهحل بهینه مینمایند. در هر گام، هر ذره با استفاده از دو بهترین مقدار به روز میشود. اولین مورد، بهترین موقعیتی است که تاکنون ذره موفق به رسیدن به آن شدهاست. موقعیت مذکور شناخته و نگهداری میشود که این بهترین مقدار نوستالژی آن ذره نیز گفته میشود که آن را با pbest نمایش میدهیم. بهترین مقدار دیگری که توسط الگوریتم مورد استفاده قرار میگیرد، بهترین موقعیتی است که تا کنون توسط جمعیت ذرات بدست آمدهاست که آن را gbest میگوییم (هوش جمعی).
پس از یافتن بهترین مقادیر، سرعت و مکان هر ذره با استفاده از رابطه ۶ و ۷به روز میشود.
رابطه 6
رابطه 7
سمت راست معادله ۶ از سه قسمت تشکیل شدهاست که قسمت اول، سرعت فعلی ذره است (



با صفر قرار دادن یا ندادن پارامترهای c1 و c2 سه حالت مختلف زیر به وجود میآید:
- هیچکدام از این دو پارامتر را صفر نگذاریم که میشود pso با لختی سرعت، هوش جمعی و نوستالژی.
- وزن نوستالژی را صفر کنیم و فقط براساس هوش جمعی و لختی عمل کنیم.
- وزن هوش جمعی را صفر کنیم و فقط براساس نوستالژی و لختی عمل کنیم.
برای مقداردهی اولیه توسط رابطه ۸ عمل میکنیم. سرعت اولیه نیز طبق ۹ صفر است.
رابطه 8
رابطه 9
شبه کد الگوریتم PSO:
For each particle
Initialize particle
End For
Do
For each particle
Calculate fitness value of the particle fp
/*updating particle’s best fitness value so far)*/
If fp is better than pBest
set current value as the new pBest
End For
/*updating population’s best fitness value so far)*/
Set gBest to the best fitness value of all particles
For each particle
Calculate particle velocity according equation
Update particle position according equation
End For While maximum iterations OR minimum error criteria is not attained
اما در مورد شرط توقف باید گفت که راههای زیر موجود است:
- تعداد تکرار معین
- رسیدن به یک شایستگی آستانه
- یک تعداد تکرار که شایستگی تغییر نکند (مثلاً اگر بعد از ۱۰ تکرار شایستگی ثابت بود و بهتر نشد).
- راه آخر بر اساس چگالی تجمیع اطراف نقطه بهینه است. به این صورت که میگوییم اگر ۸۰ درصد ذرات در فاصلهای کمتر از ۲۰ درصد بیشترین فاصله نسبت به بهترین جواب قرار داشتند، الگوریتم باید متوقف شود.
روش آخر به این صورت است که طبق رابطه ۱۰ میتوان را بدست آورد. همانطور که گفته شد
رابطه 10
مشکل اساسی اولین الگوریتم ازدحام ذرات
یک مشکل اساسی فرمول ارائه شده برای الگوریتم ازدحام ذرات اولیه اینست که دائماً سرعت افزایش مییابد و هیچ برنامهای برای کاهش آن ارائه نشده است، درصورتیکه لازم است هر چه به بهینه سراسری نزدیک میشویم سرعت کمتر شود تا ذره ما از بهینه سراسری عبور نکند.
برای این کار چند راه حل ارائه شدهاست.
استفاده از سرعت بیشینه برشی
در این روش برای جلوگیری از زیاد شدن بیش از اندازه سرعت، یک سرعت بیشینه تعریف میشود تا هرگاه سرعت به بیش از آن رسید برش داده شود.
استفاده از سرعت بیشینه تانژانت هیپربولیکی
در این روش از یک تابع تانژانت هیپربولیک برای محدود کردن سرعت به یک مقدار خاص استفاده میشود. تفاوت این حالت با حالت برشی اینست که در این حالت تابع ما مشتق پذیر در همهٔ نقاط است درحالیکه در حالت برشی مشتق پذیری از بین می رود.
در حالت برشی در نقطه برش مشتق پذیری از بین میرود؛ ولی در تانژانت هیپربولیک این مشکل وجود ندارد.
استفاده از ضریب کاهنده سرعت
در این روش از یک که باید بین ۰ و ۱ باشد، استفاده میشود. در غیر این صورت اگر بیش از ۱ باشد، سرعت افزاینده خواهد بود.
| ۱۴ |
حال تعیین کردن خود این یک مسئله است که روشهای متعددی برای آن وجود دارد.
روش اول:
| ۱۵ |
روش دوم:
| ۱۶ |
در این روش باید را طوری تعیین کنیم که کمتر از ۱ شود.
روش سوم:
| ۱۷ |
برای میتوان ۰٫۹ را انتخاب کرد و برای مقدار ۰٫۲ مناسب است.
روش چهارم:
در این روش براساس مقدار شایستگی تغییر میکند که این روش مناسب تری از روشهای بالا است.
| ۱۸ | |
| ۱۹ |
که شایستگی راهحل بهینه سراسری است.
روش پنجم:
در این روش که جدیدترین روش است یک پارامتر X خی که در کل سرعت ضرب میشود.
| ۲۰ | |
| ۲۱ | + , |
| ۲۲ | ; k ∈[۰٬۱] |
استفاده از تابعی برحسب تکرار برای سرعت بیشینه
در این روش سعی میشود تا از یک سرعت بیشینه به صورت تابعی از تکرار استفاده شود. در این روش سرعت بیشینه طبق رابطه ۱۳ برای هر بعد جداگانه حساب میشود.
| [null 13] |
این قابلیت باعث میشود که سرعت بیشینه با توجه به نیاز ما برای تنظیم وزن کاوش و انتفاع در هر تکرار مربوطه تعیین شود.
الگوریتم ازدحام ذرات آسنکرون
الگوریتم ازدحام ذرات گفته شده نوع سنکرون بود، یک نوع دیگری از این الگوریتم وجود دارد که به آن آسنکرون گویند. در این حالت پس از محاسبه شایستگی هریک از ذرات اگر بهینه سراسری عوض شد بلافاصله بهروزرسانی میشود. این کار باعث میشود که سرعت همگرایی تا حدودی افزایش یابد؛ ولی امکان پیادهسازی موازی را میگیرد.
الگوریتم ازدحام ذرات تمام آگاه
ذرات با اطلاع هم و با هماهنگی حرکت میکنند و یک ذره حرکت بقیه را نیز در حرکت خودش دخالت میدهد.
| ۲۳ |
که یک عدد تصادفی است که به هر سرعت ذره یک وزن میدهد. در این حالت طبق رابطه هر ذره کاملاً کورکورانه بردار حرکت سایر ذرات را مد نظر قرار میدهد و با گرفتن برآیندی از جهت و اندازه حرکت همه، جهت و اندازه خود را بدست میآورد.
الگوریتم ازدحام ذرات استخوان خالی
این الگوریتم نسبت به الگوریتمهای قبلی خیلی سریع تر همگرا میشود و دارای دو نسخه است که در نسخه اول سرعت به شیوه زیر محاسبه میشود.
نسخه اول:
| ۲۴ | |
| ۲۵ | |
| ۲۶ |
نسخه دوم:
در این حالت در نیمی از حالات از روش استخوان خالی و در نیمی از الگوریتم ازدحام ذرات معمول استفاده میشود.
| ۲۷ |
الگوریتم ازدحام ذرات پیش کشیدن و پس زدن
در این الگوریتم ذره به سمت بهینه سراسری جذب میشود وقتی که به مقدار آستانه اول برسد، دفع میشود تا به جستجوی بیشتری بپردازد و این دفع شدن تا جایی ادامه پیدا میکند که به آستانه دوم برسد. عملیات جذب شدن با فرمول ۳۲ ولی دفع شدن با فرمول ۳۳ صورت میگیرد.
| [null 32] | |
| [null 33] |
الگوریتم ازدحام ذرات شکار و شکارچی
هنگامی که ذرات همگرا شوند یک پارامتر ترس اعمال میکنیم با احتمال که باعث دور شدن ذرات از بهینه سراسری میشود و درنتیجه جستجو بیشتر میشود.
| ۳۴ | |
| ۳۵ |
الگوریتم ازدحام ذرات چندشروعه
در این روش عملاً یک ذره را جهش میدهیم. برای وقتی است که مقدار شایستگی در چند تکرار بهبودی ندارد.
جمعبندی
الگوریتم ازدحام ذرات دودویی
این یکی از الگوریتمهایی است که برای مسائل جایگذاری یا عدم جایگذاری استفاده میشود. برای این کار باید از یک نگاشت برای تبدیل از پیوسته به دودویی استفاده شود.
منبع
بهینهسازی ازدحام ذرات (PSO) قسمت 1
بهینهسازی ازدحام ذرات (PSO) قسمت 2










دیدگاه خود را ثبت کنید
تمایل دارید در گفتگوها شرکت کنید؟در گفتگو ها شرکت کنید.