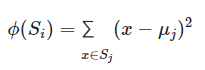بایگانی برچسب برای: vdjl

بهينه‌سازی و معرفي روش‌های آن قسمت 2

3-5-انواع روش‌هاي فرا ابتكاري برگرفته از طبيعت

1-3-5-الگوريتم ژنتيك

الگوريتم ژنتيك (Genetic Algorithm) روشي عمومي از روش‌هاي فرا ابتكاري براي بهينه‌سازي گسسته مي‌باشد كه مسائل جدول زمانبندي را حل مي‌نمايد. روش شبيه‌سازي كه در ادامه مورد بحث قرار می‌گيرد، راهبرد تكاملي نام دارد. اين روش در سال 1975 به وسيله هولند (Holland) و در سال 1989 توسط  گولدبرگ (Goldberg) ابداع شده است.

اين روش نوعي روش جستجوي همسايه است كه عملكردي مشابه ژن دارد. در طبيعت، فرايند تكامل هنگامي ايجاد مي‌شود كه چهار شرط زير برقرار باشد:

الف) يك موجود توانايي تكثير داشته باشد (قابليت توليد مثل).

ب) جمعيتي از اين موجودات قابل تكثير وجود داشته باشد.

پ) چنين وضعيتي داراي تنوع باشد.

ت) اين موجودات به وسيله قابليت‌هايي در زندگي از هم جدا شوند.

در طبيعت، گونه‌هاي متفاوتي از يك موجود وجود دارند كه اين تفاوت‌ها در كروموزوم‌هاي اين موجودات ظاهر مي‌شود و باعث تنوع در ساختار و رفتار اين موجودات مي‌شود.

اين تنوع ساختار و رفتار به نوبه خود بر زاد و ولد تأثير مي‌گذارد. موجوداتي كه قابليت‌ها و توانايي بيشتري براي انجام فعاليت‌ها در محيط دارند (موجودات متكامل‌تر)، داراي نرخ زاد و ولد بالاتري خواهند بود و طبعاً موجوداتي كه سازگاري كمتري با محيط دارند، از نرخ زاد و ولد پايين‌تري برخوردار خواهند بود. بعد از چند دوره زماني و گذشت چند نسل، جمعيت تمايل دارد كه موجوداتي را بيشتر در خود داشته باشد كه كروموزوم‌هايشان با محيط اطراف سازگاري بيشتري دارد.

در طي زمان، ساختار افراد جامعه به علت انتخاب طبيعي تغيير مي‌كند و اين نشانه تكامل جمعيت است.

6- آنيلينگ شبيه‌سازي شده

اين روش توسط متروپوليس (Metropolis) و همكاران در سال 1953 پيشنهاد شده و جهت بهينه‌سازي به وسيله وچی (Vecchi)، گلات (Gelatt) و کرک‌پاتريک (kirkpatrick ) در سال 1983 مورد بازبيني قرار گرفته است. اين روش در مسائل تاكسي تلفني كاربرد دارد.

الگوريتم آنيلينگ شبيه‌سازي شده (Simulated Annealing) در شکل عمومي، بر اساس شباهت ميان سرد شدن جامدات مذاب و حل مسائل بهينه‌سازي تركيبي به وجود آمده است. در فيزيك مواد فشرده، گرم و سرد كردن فرايندي است فيزيكي كه طي آن يك ماده جامد در ظرفي حرارت داده مي‌شود تا مايع شود؛ سپس حرارت آن بتدريج كاهش مي‌يابد. بدين ترتيب تمام ذرات فرصت مي‌يابند تا خود را در پايين‌ترين سطح انرژي منظم كنند. چنين وضعي در شرايطي ايجاد مي‌شود كه گرمادهي كافي بوده و سرد كردن نيز به آهستگي صورت گيرد. جواب حاصل از الگوريتم گرم و سرد كردن شبيه‌سازي شده، به جواب اوليه وابسته نيست و مي‌توان توسط آن جوابي نزديك به جواب بهينه به دست آورد. حد بالايي زمان اجراي الگوريتم نيز قابل تعيين است. بنابراين الگوريتم گرم و سرد كردن شبيه‌سازي شده، الگوريتمي است تكراري كه اشكالات روش‌هاي عمومي مبتني بر تكرار را ندارد.

در روش آنيلينگ شبيه‌سازي شده، به صورت پي در پي از جواب جاري به يكي از همسايه‌هاي آن انتقال صورت مي‌گيرد. اين سازوکار توسط زنجيره ماركوف به صورت رياضي قابل توصيف است. در اين روش، يك مجموعه آزمون انجام مي‌گيرد؛ اين آزمون‌ها به نحوي است كه نتيجه هر يك به نتيجه آزمون قبل وابسته است. در روش آنيلينگ شبيه‌سازي شده، منظور از يك آزمون، انتقال به نقطه جديد است و روشن است كه نتيجه انتقال به نقطه جديد تنها وابسته به مشخصات جواب جاري است.

روش جستجوي همسايه و روش آنيلينگ شبيه‌سازي شده، هر دو روش‌هاي تكراري هستند. در الگوريتم آنيلينگ شبيه‌سازي شده، هر بار كه شاخص كنترل‌كننده به مقدار نهايي خود مي‌رسد، در حقيقت يك عمليات تكراري انجام شده است. در الگوريتم جستجوي همسايه، هنگامي كه تعداد تكرارها به سمت بي‌نهايت ميل مي‌كند، روش به جواب بهينه نزديك مي‌شود. اما عملكرد الگوريتم آنيلينگ شبيه‌سازي شده سريع‌تر است.

7-شبکه‌های عصبی

شبکه‌های عصبی (Neural Networks) مصنوعی سيستم‌هاي هوشمندی هستند که از شبکه‌هاي عصبي طبيعي الهام گرفته شده‌اند. شبکه‌هاي عصبي مصنوعي در واقع تلاشي براي حرکت از سمت مدل محاسباتي فون نيومن به سمت مدلي است که با توجه به عملکرد و ويژگي‌هاي مغز انسان طراحي شده است. مدل فون نيومن گرچه هم اکنون بسيار استفاده می‌شود، اما از کمبودهايي رنج مي‌برد که تلاش شده است اين کمبودها در شبکه‌هاي عصبي مصنوعي برطرف شود.

در سال 1943 مدلی راجع به عملکرد نورون‌ها (Neuron) نوشته شد که با اندکی تغيير، امروزه بلوک اصلی سازنده اکثر شبکه‌های عصبی مصنوعی می‌باشد. عملکرد اساسی اين مدل مبتنی بر جمع کردن ورودی‌ها و به دنبال آن به وجود آمدن يک خروجی است. ورودی‌های نورون‌ها از طريق دنريت‌ها که به خروجی نورون‌های ديگر از طريق سيناپس متصل است، وارد می‌شوند. بدنه سلولی کليه اين ورودی‌ها را دريافت می‌کند و چنانچه جمع اين مقادير از مقداری که به آن آستانه گفته می‌شود بيشتر باشد، در اصطلاح برانگيخته شده يا آتش می‌کند و در اين صورت، خروجی نورون روشن يا خاموش خواهد شد.

مدل پایه ای نرون

مدل پايه‌اي نورون به صورت شکل 1-3 تعريف می‌شود.

مدل پایه ای نرون

مدل پایه ای نرون

اين مدل و برخی از کارهای مربوط به آن را بايد به عنوان شروع مطالعات تحليلی در نظر گرفت. گر چه اين مدل ساده فاقد ويژگی‌های پيچيده بدنه سلولی نورون‌های بيولوژيکی است، اما می‌توان به آن به صورت مدلی ساده از آنچه که واقعاً موجود است نگريست.

جستجوي ممنوع

روشی عمومي است كه به وسيله گلوور (Glover) در سال 1989 پيشنهاد شده و در حل مسائل برنامه‌ريزي كاري ـ خريد کاربرد دارد.

روش جستجوي ممنوع (Tabu Search)، همانند روش آنيلينگ شبيه‌سازي شده بر اساس جستجوي همسايه بنا شده است. در اين روش عملكرد حافظه انسان شبيه‌سازي شده است. حافظه انسان با به كارگيري ساختماني مؤثر و در عين حال ساده از اطلاعات، آنچه را در قبل رؤيت شده، ذخيره مي‌كند. اين مركز همچنين فهرستی از حركات منع شده را تنظيم مي‌كند و اين فهرست همواره بر اساس آخرين جستجوها منظم مي‌شود. اين روش از انجام هر گونه عمليات مجدد و تكراري جلوگيري مي‌كند.

شكل نوين جستجوي ممنوع توسط گلوور مطرح شده است. روش جستجوي مبتني بر منع، با ايجاد تغييري كوچك در روش جستجوي همسايه به وجود مي‌آيد. هدف اين روش آن است كه بخش‌هايي از مجموعه جواب كه پيش از اين بررسي نشده است، مد نظر قرار گيرد. بدين منظور حركت به جواب‌هايي كه اخيراً جستجو شده، ممنوع خواهد بود.

ساختار كلي روش جستجوي ممنوع بدين صورت است كه ابتدا يك جواب اوليه امكان‌پذير انتخاب مي‌شود؛ سپس براي جواب مربوط، بر اساس يک معيار خاص مجموعه‌اي از جواب‌هاي همسايه امكان‌پذير در نظر گرفته مي‌شود.

در گام بعد، پس از ارزيابي جواب‌هاي همسايه تعيين شده، بهترين آنها انتخاب مي‌شود و جابه‌جايي از جواب جاري به جواب همسايه انتخابي صورت مي‌گيرد. اين فرايند به همين ترتيب تكرار مي‌شود تا زماني كه شرط خاتمه تحقق يابد.

در روش جستجوي ممنوع، فهرستي وجود دارد كه جابه‌جايي‌هاي منع شده را نگهداري مي‌كند و به فهرست تابو معروف است و كاربرد اصلي آن، پرهيز از همگرا شدن به جواب‌هاي بهينه محلي است. به عبارت ديگر، به كمك فهرست تابو جابه‌جايي به جواب‌هايي كه اخيراً جستجو شده‌اند، ممنوع خواهد شد. فقط بخش‌هايي از مجموعه جواب كه پيش از اين مورد بررسي قرار نگرفته، مد نظر خواهند بود. در واقع جابه‌جايي از جواب جاري به جواب همسايه امكان‌پذير زماني انجام مي‌شود كه در فهرست تابو قرار نداشته باشد. در غير اين صورت، جواب همسايه ديگري كه در ارزيابي جواب‌هاي همسايه در رده بعدي قرار گرفته است، انتخاب شده و جابه‌جايي به آن صورت مي‌گيرد.

در روش جستجوي ممنوع بعد از هر جابه‌جايي، فهرست تابو بهنگام مي‌شود، به نحوي كه جابه‌جايي جديد به آن فهرست اضافه شده و جابه‌جايي كه تا n  تكرار مشخص در فهرست بوده است، از آن حذف مي‌شود. نحوه انتخاب مي‌تواند با توجه به شرايط و نوع مسأله متفاوت باشد.

سيستم مورچه (Ant System)

اين روش در سال 1991 توسط مانيه‌زو (Maniezzo) دوريگو (Dorigo) و کولورنی (Colorni) پيشنهاد شده است كه در حل مسأله فروشنده دوره‌گرد و مسائل تخصيص چندوجهي کاربرد دارد.

الگوريتم بهينه‌سازي كلوني مورچه‌ها از عامل‌هاي ساده‌اي كه مورچه ناميده مي‌شوند، استفاده مي‌كند تا به صورت تكراري جواب‌هايي توليد كند. مورچه‌ها می‌توانند كوتاه‌ترين مسير از يك منبع غذايي به لانه را با بهره‌گيري از اطلاعات فرموني پيدا کنند. مورچه‌ها در هنگام راه رفتن، روي زمين فرمون مي‌ريزند و با بو كشيدن فرمون ريخته شده بر روي زمين راه را دنبال مي‌كنند؛ چنانچه در طي مسير به سوي لانه به يك دوراهي برسند، از آن جايي كه هيچ اطلاعي درباره راه بهتر ندارند، راه را به تصادف برمي‌گزينند. انتظار مي‌رود به طور متوسط نيمي از مورچه‌ها مسير اول و نيمي ديگر مسير دوم را انتخاب كنند.

فرض مي‌شود كه تمام مورچه‌ها با سرعت يكسان مسير را طي كنند. از آنجا كه يك مسير كوتاه‌تر از مسير ديگر است، مورچه‌هاي بيشتري از آن مي‌گذرند و فرمون بيشتري بر روي آن انباشته مي‌شود. بعد از مدت كوتاهي مقدار فرمون روي دو مسير به اندازه‌اي مي رسد كه روي تصميم مورچه‌هاي جديد براي انتخاب مسير بهتر تأثير مي‌گذارد. از اين به بعد، مورچه‌هاي جديد با احتمال بيشتري ترجيح مي‌دهند از مسير كوتاه‌تر استفاده كنند، زيرا در نقطه تصميم‌گيري مقدار فرمون بيشتري در مسير كوتاه‌تر مشاهده مي‌كنند. بعد از مدت كوتاهي تمام مورچه‌ها اين مسير را انتخاب خواهند كرد.

منبع

مقدمه ای بر بهینه سازی و الگوریتم های موجود

هدف از بهينه‌سازي يافتن بهترين جواب قابل قبول، با توجه به محدوديت‌ها و نيازهاي مسأله است. براي يك مسأله، ممكن است جواب‌هاي مختلفي موجود باشد كه براي مقايسه آنها و انتخاب جواب بهينه، تابعي به نام تابع هدف تعريف مي‌شود. انتخاب اين تابع به طبيعت مسأله وابسته است. به عنوان مثال، زمان سفر يا هزينه از جمله اهداف رايج بهينه‌سازي شبكه‌هاي حمل و نقل مي‌باشد. به هر حال، انتخاب تابع هدف مناسب يكي از مهمترين گام‌هاي بهينه‌سازي است. گاهي در بهينه‌سازي چند هدف  به طور همزمان مد نظر قرار مي‌گيرد؛ اين گونه مسائل بهينه‌سازي را كه دربرگيرنده چند تابع هدف هستند، مسائل چند هدفي مي‌نامند. ساده‌ترين راه در برخورد با اين گونه مسائل، تشكيل يك تابع هدف جديد به صورت تركيب خطي توابع هدف اصلي است كه در اين تركيب ميزان اثرگذاري هر تابع با وزن اختصاص يافته به آن مشخص مي‌شود. هر مسأله بهينه‌سازي داراي تعدادي متغير مستقل است كه آنها را متغيرهاي طراحي می‌نامند كه با بردار n  بعدي x  نشان داده مي‌شوند.

هدف از بهينه‌سازي تعيين متغيرهاي طراحي است، به گونه‌اي كه تابع هدف كمينه يا بيشينه شود.

مسائل مختلف بهينه‌سازي  به دو دسته زير تقسيم مي‌شود:

الف) مسائل بهينه‌سازي بي‌محدوديت: در اين مسائل هدف، بيشينه يا كمينه كردن تابع هدف بدون هر گونه محدوديتي بر روي متغيرهاي طراحي مي‌باشد.

ب) مسائل بهينه‌سازي با محدوديت: بهينه‌سازي در اغلب مسائل كاربردي، با توجه به محدوديت‌هايي صورت مي‌گيرد؛ محدوديت‌هايي كه در زمينه رفتار و عملكرد يك سيستم مي‌باشد و محدوديت‌هاي رفتاري و محدوديت‌هايي كه در فيزيك و هندسه مسأله وجود دارد، محدوديت‌هاي هندسي يا جانبي ناميده مي‌شوند.

معادلات معرف محدوديت‌ها ممكن است  به صورت مساوي يا نامساوي باشند كه در هر مورد، روش بهينه‌سازي متفاوت مي‌باشد. به هر حال محدوديت‌ها، ناحيه قابل قبول در طراحي را معين مي‌كنند.

فرايند بهينه ­سازي

فرموله كردن مسئله: در اين مرحله، يك مسئله ­ي تصميم ­گيري، همراه با يك ساختار كلي از آن تعريف مي‌شود. اين ساختار كلي ممكن است خيلي دقيق نباشد اما وضعيت كلي مسئله را، كه شامل فاكتورهاي ورودي و خروجي و اهداف مسئله است، بيان مي­ كند. شفاف­ سازي و ساختاردهي به مسئله، ممكن است براي بسياري از مسايل بهينه­ سازي، كاري پيچيده باشد.

مدل­ سازي مسئله:

در اين مرحله يك مدل رياضي كلي براي مسئله، ساخته مي­ شود. مدل­سازي ممكن است از مدل­ هاي مشابه در پيشينه ­ي موضوع كمك بگيرد. اين گام موجب تجزيه مسئله به يك يا چند مدل بهينه‌سازي مي­ گردد.

بهينه­ سازي مسئله:

پس از مدل سازي مسئله، روال حل، يك راه ­حل خوب براي مسئله توليد مي­ كند. اين راه‌حل ممكن است بهينه يا تقريباً بهينه باشد. نكته ­اي كه بايد به آن توجه داشت اين است كه راه ­حل به دست آمده، راه­ حلي براي مدل طراحي شده است، نه براي مسئله ­ي واقعي. در هنگام فرموله كردن و مدلسازي ممكن است تغييراتي در مسئله واقعي به وجود آمده و مسئله­ ي جديد، نسبت به مسئله­ ي واقعي تفاوت زيادي داشته باشد.

استقرار مسئله:

راه ­حل به دست آمده توسط تصميم گيرنده بررسي مي­ شود و در صورتي كه قابل قبول باشد، مورد استفاده قرار مي­ گيرد و در صورتي كه راه­حل قابل قبول نباشد، مدل يا الگوريتم بهينه­ سازي بايد توسعه داده شده و فرايند بهينه­ سازي تكرار گردد.

الگوریتم­ های بهینه­ سازی

هدف الگوریتم­ های اکتشافی، ارائه راه حل در چارچوب یک زمان قابل قبول است که برای حل مسئله مناسب باشد، ممکن است الگوریتم اکتشافی، بهترین راه حل واقعی برای حل مسئله نبوده ولی می­ تواند راه حل نزدیک به بهترین باشد. الگوریتم ­های اکتشافی با الگوریتم­ های بهینه­ سازی برای اصلاح کارایی الگوریتم می‌توانند ترکیب شوند. الگوریتم فرا اکتشافی ترکیبی است از الگوریتم ­های اکتشافی که برای پیدا کردن، تولید یا انتخاب هر اکتشاف در هر مرحله طراحی می­شود و راه حل خوبی برای مسائلی که مشکل بهینه‌سازی دارند ارائه می‌دهد. الگوریتم­ های فرا اکتشافی برخی از فرضیات مسائل بهینه­ سازی که باید حل شود را در نظر می ­گیرد.

 روش‌هاي فرا ابتكاري برگرفته از طبيعت

الگوريتم ­هاي فراابتكاري الگوريتم ­هايي هستند كه با الهام از طبيعت، فيزيك و انسان طراحي شده ­اند و در حل بسياري از مسايل بهينه­ سازي استفاده می­ شوند. معمولاً از الگوريتم­ هاي فراابتكاري در تركيب با ساير الگوريتم­ ها، جهت رسيدن به جواب بهينه يا خروج از وضعيت جواب بهينه محلي استفاده مي­گردد. در سال‌هاي اخير يكي از مهمترين و اميدبخش‌ترين تحقيقات، «روش‌هاي ابتكاري برگرفته از طبيعت» بوده است؛ اين روش‌ها شباهت‌هايي با سيستم‌هاي اجتماعي و يا طبيعي دارند. كاربرد ‌آنها برگرفته از روش‌هاي ابتكاري پيوسته می‌باشد كه در حل مسائل مشكل تركيبي (NP-Hard) نتايج بسيار خوبی داشته است.

در ابتدا با تعريفي از طبيعت و طبيعي بودن روش‌ها شروع مي‌كنيم؛ روش‌ها برگرفته از فيزيك، زيست‌شناسي و جامعه‌شناسي هستند و به صورت زير تشكيل شده‌اند:

–         استفاده از تعداد مشخصي از سعي‌ها و كوشش‌هاي تكراري

–          استفاده از يك يا چند عامل (نرون، خرده‌ريز، كروموزوم، مورچه و غيره)

–          عمليات (در حالت چند عاملي) با يك سازوکار همكاري ـ رقابت

–          ايجاد روش‌هاي خود تغييري و خود تبديلي

طبيعت داراي دو تدبير بزرگ مي‌باشد:

1-    انتخاب پاداش براي خصوصيات فردي قوي و جزا براي فرد ضعيف‌تر؛

2-     جهش كه معرفي اعضای تصادفي و امکان تولد فرد جديد را ميسر می‌سازد.

به طور كلي دو وضعيت وجود دارد كه در روش‌هاي ابتكاري برگرفته از طبيعت ديده مي‌شود، يكي انتخاب و ديگري جهش. انتخاب ايده‌اي مبنا براي بهينه‌سازي و جهش ايده‌اي مبنا براي جستجوي پيوسته مي‌باشد.

از خصوصيات روش‌هاي ابتكاري  برگرفته از طبيعت، مي‌توان به موارد زير اشاره كرد:

1-    پديده‌اي حقيقي در طبيعت را مدل‌سازي مي‌كنند.

2-     بدون قطع مي‌باشند.

3-     اغلب بدون شرط تركيبي همانند (عامل‌هاي متعدد) را معرفي مي‌نمايند.

4-     تطبيق‌پذير هستند.

خصوصيات بالا باعث رفتاري معقول در جهت تأمين هوشمندي مي‌شود. تعريف هوشمندي نيز عبارت است از قدرت حل مسائل مشكل؛ بنابراين هوشمندي به حلمناسب مسائل بهينه‌سازي تركيبي منجر می‌شود.

برخی الگوریتم های بهینه سازی مهم عبارت انداز:

 الگوریتم بهینه سازی ازدحام ذرات

در سال 1995 ابرهارت و کنیدی براي اولین بار PSOبه عنوان یک روش جستجوي غیر قطعی براي بهینه سازي تابعی مطرح گشت این الگوریتم از حرکت دسته جمعیپرندگانی که به دنبال غذا می­باشند، الهام گرفته شده است. گروهي از پرندگان در فضايي به صورت تصادفي دنبال غذا مي­گردند. تنها يك تكه غذا در فضاي مورد بحث وجود دارد. هيچ يك از پرندگان محل غذا را نمي­دانند. يكي از بهترين استراتژي­ها مي­تواند دنبال كردن پرنده­اي باشد كه كمترين فاصله را تا غذا داشته باشد.  ايناستراتژي در واقع جانمايه الگوريتم است. هر راه­حل كه به آن يك ذره گفته مي­شود،PSO  در الگوريتم معادل يك پرنده در الگوريتم حركت جمعي پرندگان مي­باشد.هر ذره يك مقدار شايستگي دارد كه توسط يك تابع شايستگي محاسبه مي­شود. هر چه ذره در فضا­ي جستجو به هدف – غذا در مدل حركت پرندگان-  نزدیكتر باشد،شايستگي بيشتري دارد. همچنين هر ذره داراي يك سرعت است كه هدايت حركت ذره را بر عهده دارد. هرذره با دنبال كردن ذرات بهينه در حالت فعلي، به حركت خوددر فضاي مساله ادامه مي­دهد.

الگوریتم کرم شب­ تاب

الگوریتم کرم شب ­تاب به عنوان الگوریتم ذهنی مبتنی بر ازدحام، برای وظایف بهینه­سازی محدود، ارائه شده است. در این الگوریتم از رفتار تابشی کرم­های شب تابالهام گرفته شده است. کرم­های شب تاب در طبیعت به طور دسته جمعی زندگی می­کنند و همواره کرم کم نورتر به سمت کرم پرنور تر حرکت می‌کند. این الگوریتم یکرویه تکراری مبتنی بر جمعیت را با عوامل بی­شمار (تحت عنوان کرم­های شب­تاب) به کار می‌گیرد. به این عوامل امکان داده می­شود تا فضای تابع هزینه را به صورتموثرتری نسبت به جستجوی تصادفی توزیع شده، بررسی کنند. تکنیک بهینه­سازی هوشمند، مبتنی بر این فرضیه است که راه­حل یک مشکل بهینه­سازی را، می­توان بهعنوان عاملی (کرم شب­تاب) در نظر گرفت که به صورت متناسب با کیفیت آن در یک محیط تابیده می­شود. متعاقباً هر کرم شب­تاب، همتایان خود را (صرف نظر ازجنسیتشان) جذب می­کند که فضای جستجو را به صورت موثرتری بررسی می­کند. الگوریتم­های کرم شب­تاب نورهای ریتمیک و کوتاه تولید می­کنند. الگوی نوری هر کدام از کرم­های شب­تاب با یکدیگر متفاوت می­باشند. الگوریتم­های کرم شب­تاب از این نورها به دو منظور استفاده می­کنند. 1- پروسه جذب جفت­ها 2- جذب شکار. به علاوه این نورها می­توانند به عنوان یک مکانیزم محافظتی برای کرم­های شب­تاب باشند.

الگوریتم کلونی مورچگان

بهینه‌سازی گروه مورچه‌ها یا ACO همانطور که می دانیم مسئله یافتن کوتاهترین مسیر، یک مسئله بهینه سازیست که گاه حل آن بسیار دشوار است و گاه نیز بسیار زمانبر. برای مثال مسئله فروشنده دوره گرد را نیز می‌توان مطرح کرد. در این روش(ACo)، مورچه‌های مصنوعی به‌وسیلهٔ حرکت بر روی نمودار مسئله و با باقی گذاشتن نشانه‌هایی بر روی نمودار، همچون مورچه‌های واقعی که در مسیر حرکت خود نشانه‌های باقی می‌گذارند، باعث می‌شوند که مورچه‌های مصنوعی بعدی بتوانند راه‌حل‌های بهتری را برای مسئله فراهم نمایند. همچنین در این روش می‌توان توسط مسائل محاسباتی-عددی بر مبنای علم احتمالات بهترین مسیر را در یک نمودار یافت.

 الگوریتم ژنتیک

الگوریتم‌های ژنتیک، تکنیک جستجویی در علم رایانه برای یافتن راه‌حل تقریبی برای بهینه‌سازی و مسائل جستجو است. الگوریتم ژنتیک نوع خاصی از الگوریتم‌های تکامل است که از تکنیک‌های زیست‌شناسی فرگشتی مانند وراثت و جهش استفاده می‌کند. این الگوریتم برای اولین بار توسط جان هنری هالند معرفی شد. در واقع الگوریتم‌های ژنتیک از اصول انتخاب طبیعی داروین برای یافتن فرمول بهینه جهت پیش‌بینی یا تطبیق الگو استفاده می‌کنند. الگوریتم‌های ژنتیک اغلب گزینه خوبی برای تکنیک‌های پیش‌بینی بر مبنای رگرسیون هستند. در هوش مصنوعی الگوریتم ژنتیک (یا GA) یک تکنیک برنامه‌نویسی است که از تکامل ژنتیکی به عنوان یک الگوی حل مسئله استفاده می‌کند. مسئله‌ای که باید حل شود دارای ورودی‌هایی می‌باشد که طی یک فرایند الگوبرداری شده از تکامل ژنتیکی به راه‌حلها تبدیل می‌شود سپس راه حلها بعنوان کاندیداها توسط تابع ارزیاب (Fitness Function) مورد ارزیابی قرار می‌گیرند و چنانچه شرط خروج مسئله فراهم شده باشد الگوریتم خاتمه می‌یابد. الگوریتم ژنتیک بطور کلی یک الگوریتم مبتنی بر تکرار است که اغلب بخش‌های آن به صورت فرایندهای تصادفی انتخاب می‌شوند.

منبع
بهينه‌سازی و معرفي روش‌های آن قسمت 1
بهينه‌سازی و معرفي روش‌های آن قسمت 2
بهينه‌سازی و معرفي روش‌های آن قسمت 3

/0 دیدگاه /توسط

خوشه بندی k میانگین (k-means Clustering) قسمت 1

از مهم‌ترین تکنیک‌های عملی داده‌کاوی که کاربرد زیادی در علوم مختلف دارد، می توان به «خوشه بندی k-میانگین» (K-means Clustering)  اشاره کرد، که با توجه به بار محاسباتی زیاد آن، استفاده از کامپیوتر در انجام این فرآیند، کمک شایانی به کاربران می‌کند. در این راستا زبان برنامه‌نویسی و محاسباتی R قابلیت انجام این گونه محاسبات را دارد و به محققین در تحلیل خوشه‌بندی تفکیکی بر مبنای روش K-میانگین، کمک شایانی می‌کند. در این متن به بررسی روش خوشه‌بندی با استفاده از دستورات مربوط به این زبان برنامه‌نویسی می‌پردازیم و با البته با مفاهیم اولیه خوشه‌بندی k-میانگین نیز آشنا می‌شویم.

خوشه‌بندی k-میانگین

روش‌‌ها و الگوریتم‌های متعددی برای تبدیل اشیاء به گروه‌های همشکل یا مشابه وجود دارد. الگوریتم k-میانگین یکی از ساده‌ترین و محبوب‌ترین الگوریتم‌هایی است که در «داده‌کاوی» (Data Mining) بخصوص در حوزه «یادگیری نظارت نشده» (Unsupervised Learning) به کار می‌رود.

معمولا در حالت چند متغیره، باید از ویژگی‌های مختلف اشیا به منظور طبقه‌بندی و خوشه‌ کردن آن‌ها استفاده کرد. به این ترتیب با داده‌های چند بعدی سروکار داریم که معمولا به هر بعد از آن، ویژگی یا خصوصیت گفته می‌شود. با توجه به این موضوع، استفاده از توابع فاصله مختلف در این جا مطرح می‌شود. ممکن است بعضی از ویژگی‌های اشیا کمی و بعضی دیگر کیفی باشند. به هر حال آنچه اهمیت دارد روشی برای اندازه‌گیری میزان شباهت یا عدم شباهت بین اشیاء است که باید در روش‌های خوشه‌بندی لحاظ شود.

الگوریتم خوشه‌بندی k-میانگین از گروه روش‌های خوشه‌بندی تفکیکی (Partitioning Clustering) محسوب می‌شود و درجه پیچیدگی محاسباتی آن برابر با O(ndk+1) است، به شرطی که n تعداد اشیاء، d بعد ویژگی‌ها و k تعداد خوشه‌ها باشد. همچنین پیچیدگی زمانی برای این الگوریتم برابر با O(nkdi) است، که البته منظور از i‌ تعداد تکرارهای الگوریتم برای رسیدن به جواب بهینه است.

در خوشه‌بندی k-میانگین از بهینه‌سازی یک تابع هدف (Object Function) استفاده می‌شود. پاسخ‌های حاصل از خوشه‌بندی در این روش، ممکن است به کمک کمینه‌سازی (Minimization) یا بیشینه‌سازی (Maximization) تابع هدف صورت گیرد. به این معنی که اگر ملاک «میزان فاصله» (Distance Measure) بین اشیاء باشد، تابع هدف براساس کمینه‌سازی خواهد بود پاسخ عملیات خوشه‌بندی، پیدا کردن خوشه‌هایی است که فاصله بین اشیاء هر خوشه کمینه باشد. در مقابل، اگر از تابع مشابهت (Dissimilarity Function) برای اندازه‌گیری مشابهت اشیاء استفاده شود، تابع هدف را طوری انتخاب می‌کنند که پاسخ خوشه‌بندی مقدار آن را در هر خوشه بیشینه کند.

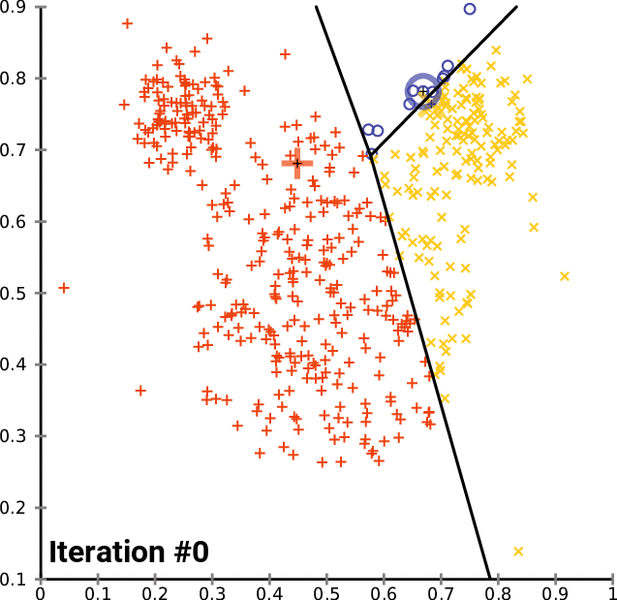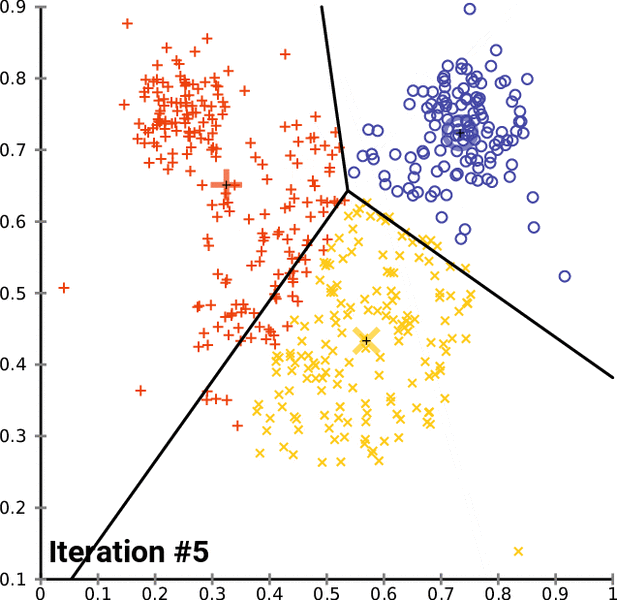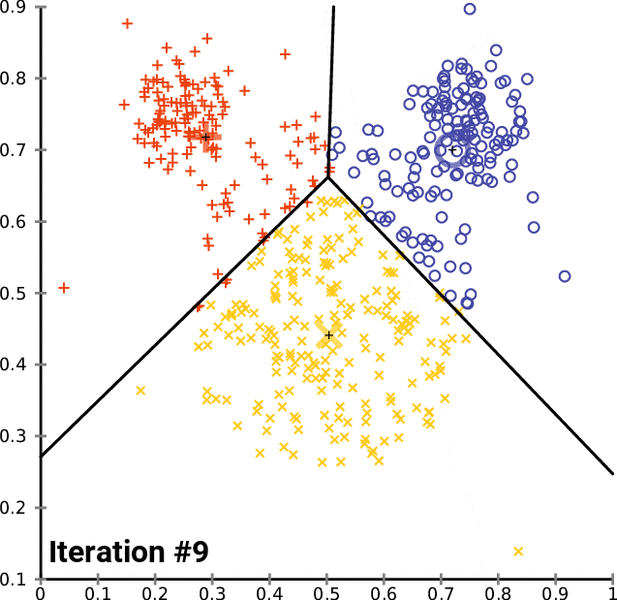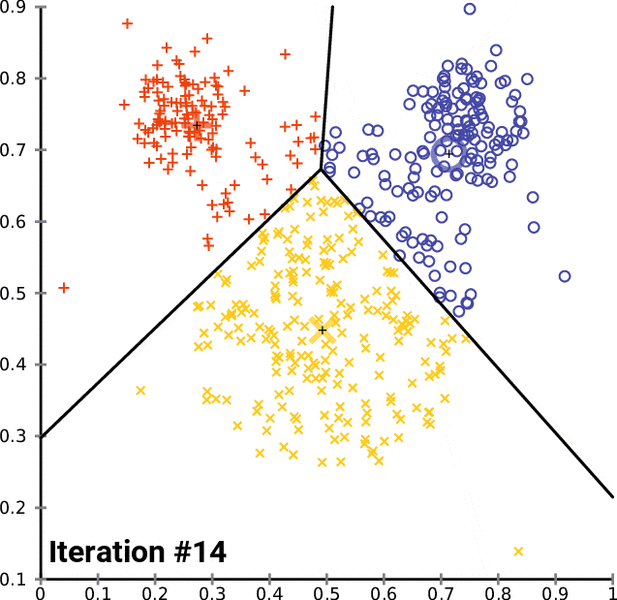
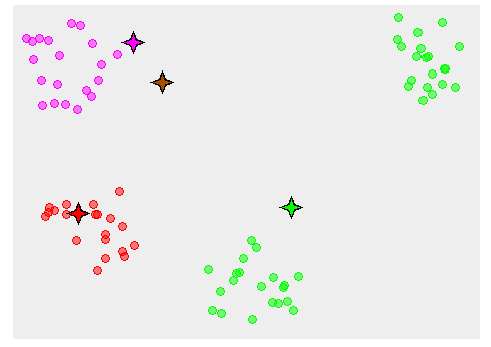
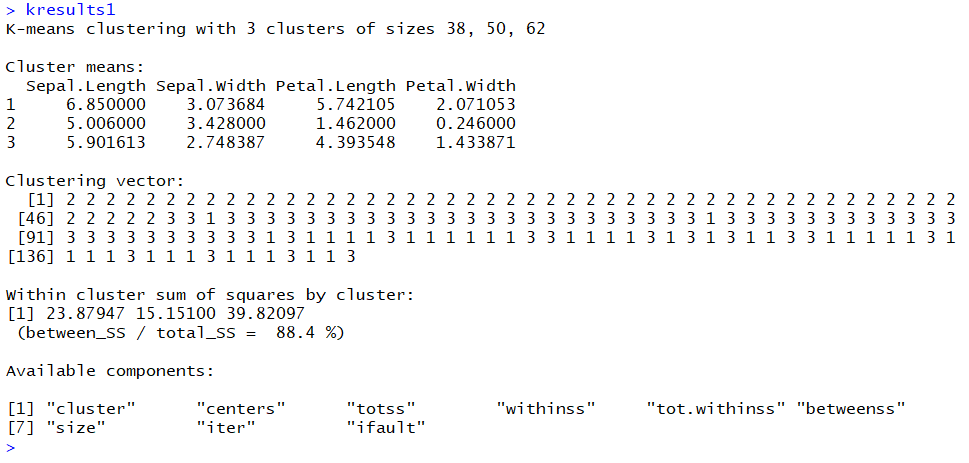
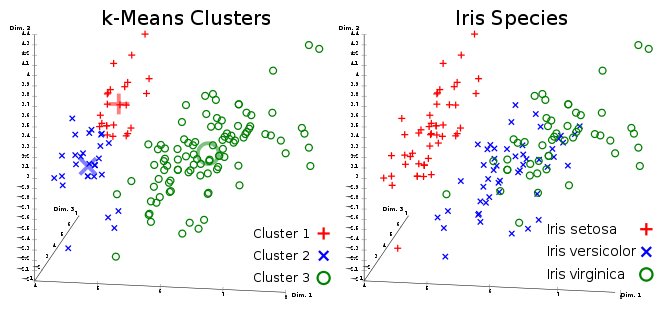
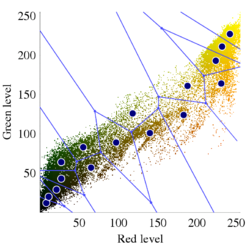
خوشه‌بندی k-میانگین روش‌‌ها و الگوریتم‌های متعددی برای تبدیل اشیاء به گروه‌های همشکل یا مشابه وجود دارد. الگوریتم k-میانگین یکی از ساده‌ترین و محبوب‌ترین الگوریتم‌هایی است که در «داده‌کاوی» (Data Mining) بخصوص در حوزه «یادگیری نظارت نشده» (Unsupervised Learning) به کار می‌رود. معمولا در حالت چند متغیره، باید از ویژگی‌های مختلف اشیا به منظور طبقه‌بندی و خوشه‌ کردن آن‌ها استفاده کرد. به این ترتیب با داده‌های چند بعدی سروکار داریم که معمولا به هر بعد از آن، ویژگی یا خصوصیت گفته می‌شود. با توجه به این موضوع، استفاده از توابع فاصله مختلف در این جا مطرح می‌شود. ممکن است بعضی از ویژگی‌های اشیا کمی و بعضی دیگر کیفی باشند. به هر حال آنچه اهمیت دارد روشی برای اندازه‌گیری میزان شباهت یا عدم شباهت بین اشیاء است که باید در روش‌های خوشه‌بندی لحاظ شود. الگوریتم خوشه‌بندی k-میانگین از گروه روش‌های خوشه‌بندی تفکیکی (Partitioning Clustering) محسوب می‌شود و درجه پیچیدگی محاسباتی آن برابر با O ( n d k + 1 ) است، به شرطی که n تعداد اشیاء، d بعد ویژگی‌ها و k تعداد خوشه‌ها باشد. همچنین پیچیدگی زمانی برای این الگوریتم برابر با O ( n k d i ) است، که البته منظور از i‌ تعداد تکرارهای الگوریتم برای رسیدن به جواب بهینه است. در خوشه‌بندی k-میانگین از بهینه‌سازی یک تابع هدف (Object Function) استفاده می‌شود. پاسخ‌های حاصل از خوشه‌بندی در این روش، ممکن است به کمک کمینه‌سازی (Minimization) یا بیشینه‌سازی (Maximization) تابع هدف صورت گیرد. به این معنی که اگر ملاک «میزان فاصله» (Distance Measure) بین اشیاء باشد، تابع هدف براساس کمینه‌سازی خواهد بود پاسخ عملیات خوشه‌بندی، پیدا کردن خوشه‌هایی است که فاصله بین اشیاء هر خوشه کمینه باشد. در مقابل، اگر از تابع مشابهت (Dissimilarity Function) برای اندازه‌گیری مشابهت اشیاء استفاده شود، تابع هدف را طوری انتخاب می‌کنند که پاسخ خوشه‌بندی مقدار آن را در هر خوشه بیشینه کند. معمولا زمانی که هدف کمینه‌سازی باشد، تابع هدف را «تابع هزینه» (Cost Function) نیز می‌نامند. روش خوشه بندی k-میانگین، توسط «مک‌کوئین» (McQueen) جامعه شناس و ریاضیدان در سال ۱۹۶۵ ابداع و توسط دیگر دانشمندان توسعه و بهینه شد. برای مثال در سال 1957 نسخه‌ دیگری از این الگوریتم به عنوان الگوریتم استاندارد خوشه‌بندی k-میانگین، توسط «لوید» (Lloyd) در آزمایشگاه‌های بل (Bell Labs) برای کدگذاری پالس‌ها ایجاد شد که بعدها در سال 1982 منتشر گردید. این نسخه از الگوریتم خوشه‌بندی، امروزه در بیشتر نرم‌افزارهای رایانه‌ای که عمل خوشه‌بندی k-میانگین را انجام می‌دهند به صورت استاندارد اجرا می‌شود. در سال 1956 «فورجی» (W.Forgy) به طور مستقل همین روش را ارائه کرد و به همین علت گاهی این الگوریتم را با نام لوید-فورجی می‌شناسند. همچنین روش هارتیگان- ونگ (Hartigan-Wong) که در سال ۱۹۷۹ معرفی شد یکی از روش‌هایی است که در تحقیقات و بررسی‌های داده‌کاوی مورد استفاده قرار می‌گیرد. تفاوت در این الگوریتم‌ها در مرحله آغازین و شرط همگرایی الگوریتم‌ها است ولی در بقیه مراحل و محاسبات مانند یکدیگر عمل می‌کنند. به همین علت همگی را الگوریتم‌های خوشه‌بندی k-میانگین می‌نامند. روش خوشه‌بندی k-میانگین فرض کنید مشاهدات ( x 1 , x 2 , … , x n ) که دارای d بعد هستند را باید به k بخش یا خوشه تقسیم کنیم. این بخش‌ها یا خوشه‌ها را با مجموعه‌ای به نام S = { S 1 , S 2 , … , S k } می‌شناسیم. اعضای خوشه‌ها باید به شکلی از مشاهدات انتخاب شوند که تابع «مجموع مربعات درون خوشه‌ها» (within-cluster sum of squares- WCSS) که در حالت یک بعدی شبیه واریانس است، کمینه شود. بنابراین، تابع هدف در این الگوریتم به صورت زیر نوشته می‌شود. a r g m i n S k ∑ i = 1 ∑ x ∈ S i ∥ x − μ i ∥ 2 = a r g m i n S k ∑ i = 1 | S i | Var S i در اینجا منظور از μ i میانگین خوشه S i و | S i | تعداد اعضای خوشه iام است. البته می‌توان نشان داد که کمینه کردن این مقدار به معنی بیشینه‌سازی میانگین مربعات فاصله بین نقاط در خوشه‌های مختلف (between-Cluster sum of Squares- BCSS) است زیرا طبق قانون واریانس کل، با کم شدن مقدار WCSS، مقدار BCSS افزایش می‌یابد، زیرا واریانس کل ثابت است. در ادامه به بررسی روش خوشه بندی k-میانگین به روش لوید-فورجی (استاندارد) و هارتیگان-ونگ می‌پردازیم. خوشه‌بندی k-میانگین با الگوریتم لوید (Lloyd’s Algorithm) به عنوان یک الگوریتم استاندارد برای خوشه‌بندی k-میانگین از الگوریتم لوید بخصوص در زمینه علوم کامپیوتر، استفاده می‌شود. ابتدا به علائمی که در این رابطه به کار می‌رود، اشاره می‌کنیم. m ( i ) j : میانگین مقدارهای مربوط به خوشه jام در تکرار iام از الگوریتم را با این نماد نشان می‌دهیم. S ( i ) j : مجموعه اعضای خوشه jام در تکرار iام الگوریتم. الگوریتم لوید را با توجه به نمادهای بالا می‌توان به دو بخش تفکیک کرد. ۱- بخش مقدار دهی ( A s s i g n m e n t S t e p )، ۲- بخش به روز رسانی (Update Step). حال به بررسی مراحل اجرای این الگوریتم می‌پردازیم. در اینجا فرض بر این است که نقاط مرکزی اولیه یعنی m ( 1 ) 1 , m ( 1 ) 2 , ⋯ , m ( 1 ) k داده شده‌اند. بخش مقدار دهی: هر مشاهده یا شی را به نزدیکترین خوشه نسبت می‌دهیم. به این معنی که فاصله اقلیدسی هر مشاهده از مراکز، اندازه گرفته شده سپس آن مشاهده عضو خوشه‌ای خواهد شد که کمترین فاصله اقلیدسی را با مرکز آن خوشه دارد. این قانون را به زبان ریاضی به صورت S ( t ) i = { x p : ∥ ∥ x p − m ( t ) i ∥ ∥ 2 ≤ ∥ ∥ x p − m ( t ) j ∥ ∥ 2 ∀ j , 1 ≤ j ≤ k } می‌نویسیم. بخش به روز رسانی: میانگین خوشه‌های جدید محاسبه می‌شود. در این حالت داریم: m ( t + 1 ) i = 1 | S ( t ) i | ∑ x j ∈ S ( t ) i x j توجه داشته باشید که منظور از | S ( t ) i | تعداد اعضای خوشه iام است. الگوریتم زمانی متوقف می‌شود که مقدار برچسب عضویت مشاهدات تغییری نکند. البته در چنین حالتی هیچ تضمینی برای رسیدن به جواب بهینه (با کمترین مقدار برای تابع هزینه) وجود ندارد. کاملا مشخص است که در رابطه بالا،‌ فاصله اقلیدسی بین هر نقطه و مرکز خوشه ملاک قرار گرفته است. از این جهت از میانگین و فاصله اقلیدسی استفاده شده که مجموع فاصله اقلیدسی نقاط از میانگینشان کمترین مقدار ممکن نسبت به هر نقطه دیگر است. نکته: ممکن است فاصله اقلیدسی یک مشاهده از دو مرکز یا بیشتر، برابر باشد ولی در این حالت آن شئ فقط به یکی از این خوشه‌ها تعلق خواهد گرفت. تصویر زیر یک مثال برای همگرایی الگوریتم لوید محسوب می‌شود که مراحل اجرا در آن دیده می‌شود. همانطور که مشخص است الگوریتم با طی ۱۴ مرحله به همگرایی می‌رسد و دیگر میانگین خوشه‌ها تغییری نمی‌یابد. البته ممکن است که این نقاط نتیجه تابع هزینه را بطور کلی (Global) کمینه نکنند زیرا روش k-میانگین بهینه‌سازی محلی (Local Optimization) را به کمک مشتق‌گیری و محاسبه نقاط اکستریمم اجرا می‌کند. K-means_convergence همگرایی الگوریتم k-میانگین نکته: به نقاط مرکزی هر خوشه مرکز (Centroid) گفته می‌شود. ممکن است این نقطه یکی از مشاهدات یا غیر از آن‌ها باشد. مشخص است که در الگوریتم لوید، k مشاهده به عنوان مرکز خوشه‌ها (Centroids) در مرحله اول انتخاب شده‌اند ولی در مراحل بعدی، مقدار میانگین هر خوشه نقش مرکز را بازی می‌کند. خوشه‌بندی k-میانگین با الگوریتم هارتیگان-ونگ (Hartigan-Wong) یکی از روش‌های پیشرفته و البته با هزینه محاسباتی زیاد در خوشه‌بندی k-میانگین، الگوریتم هارتیگان-ونگ است. برای آشنایی با این الگوریتم بهتر است ابتدا در مورد نمادهایی که در ادامه خواهید دید توضیحی ارائه شود. ϕ ( S j ) : از این نماد برای نمایش «تابع هزینه» برای خوشه S j استفاده می‌کنیم. این تابع در خوشه‌بندی k-میانگین برابر است با: ϕ ( S i ) = ∑ x ∈ S j ( x − μ j ) 2 S j : از آنجایی که هدف از این الگوریتم، تفکیک اشیاء به k گروه مختلف است، گروه‌ها یا خوشه‌ها در مجموعه‌ای با نام S قرار دارند و داریم، S = { S 1 , S 2 , ⋯ , S k } . μ j : برای نمایش میانگین خوشهjام از این نماد استفاده می‌شود. بنابراین خواهیم داشت: μ j = ∑ x ∈ S j x n j n j : این نماد تعداد اعضای خوشه jام را نشان می‌دهد. بطوری که j = { 1 , 2 , ⋯ , k } است. البته مشخص است که در اینجا تعداد خوشه‌ها را با k‌ نشان داده‌ایم. مراحل اجرای الگوریتم در خوشه‌بندی k-میانگین با الگوریتم هارتیگان می‌توان مراحل اجرا را به سه بخش تقسیم کرد: ۱- بخش مقدار دهی اولیه ( A s s i g n m e n t S t e p ) ، ۲- بخش به روز رسانی ( U p d a t e S t e p )، ۳- بخش نهایی (Termination). در ادامه به بررسی این بخش‌ها پرداخته می‌شود. بخش مقدار دهی اولیه: در الگوریتم هارتیگان-ونگ، ابتدا مشاهدات و یا اشیاء به طور تصادفی به k گروه یا خوشه تقسیم می‌شوند. به این کار مجموعه S با اعضایی به صورت { S j } j ∈ { i , ⋯ , k } مشخص می‌شود. بخش به روز رسانی: فرض کنید که مقدارهای n و m از اعداد ۱ تا k انتخاب شده باشد. مشاهده یا شیئ از خوشه nام را در نظر بگیرید که تابع Δ ( m , n , x ) = ϕ ( S n ) + ϕ ( S m ) − Φ ( S n ∖ { x } ) − ϕ ( S m ∪ { x } ) را کمینه سازد، در چنین حالتی مقدار x از خوشه nام به خوشه mام منتقل می‌شود. به این ترتیب شی مورد نظر در S m قرار گرفته و خواهیم داشت x ∈ S m . بخش نهایی: زمانی که به ازای همه n,m,x مقدار Δ ( m , n , x ) بزرگتر از صفر باشد، الگوریتم خاتمه می‌یابد. نکته: منظور از نماد ϕ ( S n ∖ { x } ) محاسبه تابع هزینه در زمانی است که مشاهده x از مجموعه S n خارج شده باشد. همچنین نماد ϕ ( S m ∪ { x } ) به معنی محاسبه تابع هزینه در زمانی است که مشاهده x به خوشه S m اضافه شده باشد. در تصویر زیر مراحل اجرای الگوریتم هارتیگان به خوبی نمایش داده شده است. هر تصویر بیانگر یک مرحله از اجرای الگوریتم است. نقاط رنگی نمایش داده شده، همان مشاهدات هستند. هر رنگ نیز بیانگر یک خوشه است. در تصویر اول مشخص است که در بخش اول از الگوریتم به طور تصادفی خوشه‌بندی صورت پذیرفته. ولی در مراحل بعدی خوشه‌ها اصلاح شده و در انتها به نظر می‌رسد که بهترین تفکیک برای مشاهدات رسیده‌ایم. در تصویر آخر نیز مشخص است که مراکز خوشه‌ها، محاسبه و ثابت شده و دیگر بهینه‌سازی صورت نخواهد گرفت. به این ترتیب پاسخ‌های الگوریتم با طی تکرار ۵ مرحله به همگرایی می‌رسد. hartigan algorithm الگوریتم هارتیگان بخش مقدار دهی اولیه hartigan algorithm الگوریتم هارتیگان تکرار ۱ hartigan algorithm الگوریتم هارتیگان تکرار ۲ hartigan algorithm الگوریتم هارتیگان تکرار ۳ hartigan algorithm الگوریتم هارتیگان تکرار ۴ hartigan algorithm الگورییتم هارتیگان تکرار ۵ اجرای این الگوریتم‌ها با استفاده از دستورات زبان برنامه‌نویسی R برای استفاده از دستورات و فرمان‌های مربوط به خوشه‌بندی k-میانگین، باید بسته یا Package مربوط به خوشه‌بندی kmeans به اسم stats را در R نصب کرده باشد. البته از آنجایی این بسته بسیار پرکاربرد است،‌ معمولا به طور خودکار فراخوانی شده است. کدهای زیر نشانگر استفاده از الگوریتم خوشه‌بندی توسط روش‌های مختلف آن است. library(stats) data=iris[,1:4] method=c("Hartigan-Wong", "Lloyd", "MacQueen") k=3 kresults1=kmeans(data,k,algorithm = method[1]) kresults2=kmeans(data,k,algorithm=method[2]) kresults3=kmeans(data,k,algorithm=method[3]) kresults1 kresults2 kresults3 1 2 3 4 5 6 7 8 9 10 11 12 library(stats) data=iris[,1:4] method=c("Hartigan-Wong", "Lloyd", "MacQueen") k=3 kresults1=kmeans(data,k,algorithm = method[1]) kresults2=kmeans(data,k,algorithm=method[2]) kresults3=kmeans(data,k,algorithm=method[3]) kresults1 kresults2 kresults3 با توجه به داده‌های iris که مربوط به اندازه و ابعاد کاسبرگ و گلبرگ سه نوع گل مختلف است، خوشه‌بندی به سه دسته انجام شده است. اطلاعات مربوط به ۱۰ سطر اول این مجموعه داده،‌ به صورت زیر است. با اجرای کدهای نوشته شده، خوشه‌بندی انجام شده و نتابج تولید می‌شوند. به عنوان مثال می‌توان خروجی را برای kresult1 که انجام خوشه بندی توسط الگوریتم هارتیگان است به صورت زیر مشاهده کرد: iris clustering همانطور که دیده می‌شود، در سطر اول تعداد اعضای هر خوشه، نمایش داده شده است. در بخش دوم که با سطر ۱ و ۲ و ۳ مشخص شده،‌ مراکز هر سه خوشه برحسب ویژگی‌های (طول و عرض کاسبرگ و طول و عرض گلبرگ) محاسبه شده و در قسمت Cluster Vector نیز برچسب خوشه هر کدام از مشاهدات دیده می‌شود. در انتها نیز مجموع مربعات فاصله درون خوشه‌ای (مجموع فاصله هر مشاهده از مرکز خوشه) استخراج شده و درصد یا شاخص ارزیابی خوشه‌بندی بر اساس نسبت مربعات بین خوشه‌ها به مربعات کل دیده می‌شود. این مقدار برای این حالت برابر ۸۸.۴٪ است که نشان می‌دهد بیشتر پراکندگی (total_ss) توسط پراکندگی بین خوشه‌ها (between_ss) بیان شده است. پس به نظر خوشه‌بندی مناسب خواهد بود. پس اختلاف بین گروه‌ها ناشی از خوشه‌های است که مشاهدات را به دسته‌‌های جداگانه تفکیک کرده. همچنین در کدها مشخص است که تعداد خوشه‌های در متغیر k ثبت و به کار رفته است. در شکل دیگری از دستور kmeans می‌توان به جای معرفی تعداد خوشه‌ها از مراکز دلخواه که با تعداد خوشه‌ها مطابقت دارد، استفاده کرد. برای مثال اگر برنامه به صورت زیر نوشته شود، الگوریتم ابتدا نقاط معرفی شده را به عنوان نقاط مرکزی (Centroids) به کار گرفته و سپس مراحل بهینه سازی را دنبال می‌کند. از آنجا که سه نقطه مبنا قرار گرفته، الگوریتم متوجه می‌شود که باید مشاهدات به سه خوشه تفکیک شود. library(stats) data=iris[,1:4] method=c("Hartigan-Wong", "Lloyd", "MacQueen") c1=c(6,4,5,3) c2=c(5,3,1,0) c3=c(6,2,4,2) centers=rbind(c1,c2,c3) kresults1=kmeans(x = data,centers = centers,algorithm = method[1]) kresults2=kmeans(x = data,centers = centers,algorithm=method[2]) kresults3=kmeans(x = data,centers = centers,algorithm=method[3]) kresults1 kresults2 kresults3 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 library(stats) data=iris[,1:4] method=c("Hartigan-Wong", "Lloyd", "MacQueen") c1=c(6,4,5,3) c2=c(5,3,1,0) c3=c(6,2,4,2) centers=rbind(c1,c2,c3) kresults1=kmeans(x = data,centers = centers,algorithm = method[1]) kresults2=kmeans(x = data,centers = centers,algorithm=method[2]) kresults3=kmeans(x = data,centers = centers,algorithm=method[3]) kresults1 kresults2 kresults3 در تصویر زیر نتیجه خوشه بندی k-میانگین را برای داده‌های iris توسط یک نمودار مشاهده می‌کنید. البته باید توجه داشت که این نمودار دو بعدی است در حالیکه داده‌ها، دارای چهار ویژگی هستند. به کمک روش‌های آماری مانند تجزیه به مولفه‌های اصلی (PCA) ابعاد مسئله کاهش یافته تا در سه بعد روی نمودار نمایش داده شود. سمت راست تصویر گروه‌های واقعی و سمت چپ نتیجه خوشه‌بندی دیده می‌شود. نقاطی که در خوشه‌ها به درستی تشخیص داده نشده‌اند، باعث افزایش خطای خوشه‌بندی خواهند شد. کاربردها از الگوریتم خوشه‌بندی k-میانگین در «بخش‌بندی بازار کسب و کار» (market Segmentation)، «دسته‌بندی مشتریان» (Customer Segmentation)، «بینایی رایانه‌ای» (Computer Vision) و «زمین‌آمار (Geostatistics) استفاده می شود. برای مثال در تشخیص تعداد رنگ و یا فشرده سازی تصاویر برحسب رنگ‌ها می‌توان از این الگوریتم‌ها استفاده کرد. در تصویر بالا گل رز زرد رنگی دیده می‌شود که در یک محیط سبز قرار گرفته است. با استفاده از الگوریتم‌های خوشه‌بندی می‌توان تعداد رنگ‌ها را کاهش داده و از حجم تصاویر کاست. در تصویر زیر دسته بندی رنگ‌های گل رز دیده می‌شود. در این تصویر، هر طیف رنگ براساس میزان رنگ قرمز و سبز، بوسیله «سلول‌های ورونوی» (Voronoi Cell) تقسیم‌بندی شده است. این تقسیم‌بندی می‌تواند توسط الگوریتم‌ها خوشه‌بندی k-میانگین صورت گرفته باشد. در کل تصویر نیز، طیف رنگ‌های مختلف برای تصویر گل رز در یک «نمودار ورونوی» (Voronoi diagram) نمایش داده شده است که خوشه‌ها را بیان می‌کند. معایب و مزایای خوشه‌بندی k-میانگین از آنجایی که در این روش خوشه‌بندی، محاسبه فاصله بین نقاط توسط تابع فاصله اقلیدسی انجام می‌شود، از این الگوریتم‌ها به صورت استاندارد، فقط برای مقدارهای عددی (و نه ویژگی‌های کیفی) می‌توان استفاده کرد. از طرف دیگر با توجه به محاسبات ساده و سریع آن‌ها،‌ پرکاربرد و موثر است. از طرف دیگر نسخه‌های تعمیم یافته از روش خوشه بندی k-میانگین نیز وجود دارد که با توابع فاصله دیگر مانند فاصله منهتن و یا فاصله‌هایی که برای داده‌های باینری قابل استفاده است، مراحل خوشه‌بندی را انجام می‌دهد. به منظور ارزیابی نتایج خوشه‌بندی از معیارهای متفاوتی کمک گرفته می‌شود. ممکن است از قبل برچسب خوشه‌ها مشخص باشد و بخواهیم کارایی الگوریتم را با توجه به مقایسه برچسب‌های واقعی و حاصل از خوشه‌بندی، اندازه‌گیری کنیم. در این حالت، شاخص‌های ارزیابی بیرونی، بهترین راهنما و معیار برای سنجش صحت نتایج خوشه‌بندی محسوب می‌شوند. معمولا به این برچسب‌ها، استاندارد طلایی (Golden Standard) و در کل چنین عملی را ارزیابی Benchmark می‌گویند. برای مثال شاخص رَند (Rand Index) یکی از این معیارها و شاخص‌های بیرونی است که از محبوبیت خاصی نیز برخوردار است. از طرف دیگر اگر هیچ اطلاعات اولیه از ساختار و دسته‌بندی مشاهدات وجود نداشته باشد، فقط ملاک ارزیابی، می‌تواند اندازه‌هایی باشد که میزان شباهت درون خوشه‌ها و یا عدم شباهت یا فاصله بین خوشه‌ها را اندازه می‌گیرند. بنابراین برای انتخاب بهتر و موثرترین روش خوشه‌بندی از میزان شباهت درون خوشه‌ها و شباهت بین خوشه‌ها استفاده می‌شود. روشی که دارای میزان شباهت بین خوشه‌ای کم و شباهت درون خوشه‌ای زیاد باشد مناسب‌ترین روش خواهد بود. این معیارها را به نام شاخص‌های ارزیابی درونی می‌شناسیم. به عنوان مثال شاخص نیم‌رخ (silhouette) یکی از این معیارها است که شاخصی برای سنجش مناسب بودن تعلق هر مشاهده به خوشه‌اش ارائه می‌دهد. به این ترتیب معیاری برای اندازه‌گیری کارایی الگوریتم خوشه‌بندی بدست می‌آید. اگر این مطلب برایتان مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند: مجموعه آموزش‌های یادگیری ماشین و بازشناسی الگو مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی آموزش خوشه بندی K میانگین (K-Means) با نرم افزار SPSS آموزش خوشه بندی تفکیکی با نرم افزار R آموزش خوشه بندی سلسله مراتبی با SPSS آشنایی با خوشه‌بندی (Clustering) و شیوه‌های مختلف آن روش‌ های ارزیابی نتایج خوشه‌ بندی (Clustering Performance) — معیارهای درونی (Internal Index) روش‌ های ارزیابی نتایج خوشه‌ بندی (Clustering Performance) — معیارهای بیرونی (External Index) ^^ telegram twitter به اشتراک بگذارید: منبع وبلاگ فرادرسWikipedia بر اساس رای 1 نفر آیا این مطلب برای شما مفید بود؟ بلیخیر نظر شما چیست؟ نشانی ایمیل شما منتشر نخواهد شد. بخش‌های موردنیاز علامت‌گذاری شده‌اند * متن نظر * نام شما * ایمیل شما * پایتخت ایران کدام شهر است؟ برچسب‌ها clusterClusteringclustering algorithmcost functiondata miningforgy algorithmhartigan-wong algorithmk-meanslloyd algorithmmaximizationMcQueen algorithmminimizationpartitioning algorithmunsupervise learningتابع هدفتابع هزینهتعداد خوشهخوشه بندیخوشه بندی K میانگینخوشه بندی در آمارخوشه‌بندیخوشه‌بندی k-میانگینمربعات بین خوشهمربعات درون خوشهمعیارهای ارزیابی خوشه عضویت در خبرنامه ایمیل * آموزش برنامه نویسی آموزش متلب Matlab نرم‌افزارهای مهندسی برق نرم‌افزارهای مهندسی عمران نرم‌افزارهای مهندسی مکانیک نرم‌افزارهای مهندسی صنایع

 

معمولا زمانی که هدف کمینه‌سازی باشد، تابع هدف را «تابع هزینه» (Cost Function) نیز می‌نامند.

روش خوشه بندی k-میانگین، توسط «مک‌کوئین» (McQueen) جامعه شناس و ریاضیدان در سال ۱۹۶۵ ابداع و توسط دیگر دانشمندان توسعه و بهینه شد. برای مثال در سال 1957 نسخه‌ دیگری از این الگوریتم به عنوان الگوریتم استاندارد خوشه‌بندی k-میانگین، توسط «لوید» (Lloyd) در آزمایشگاه‌های بل (Bell Labs) برای کدگذاری پالس‌ها ایجاد شد که بعدها در سال 1982 منتشر گردید. این نسخه از الگوریتم خوشه‌بندی، امروزه در بیشتر نرم‌افزارهای رایانه‌ای که عمل خوشه‌بندی k-میانگین را انجام می‌دهند به صورت استاندارد اجرا می‌شود. در سال 1956 «فورجی» (W.Forgy) به طور مستقل همین روش را ارائه کرد و به همین علت گاهی این الگوریتم را با نام لوید-فورجی می‌شناسند. همچنین روش هارتیگان- ونگ (Hartigan-Wong) که در سال ۱۹۷۹ معرفی شد یکی از روش‌هایی است که در تحقیقات و بررسی‌های داده‌کاوی مورد استفاده قرار می‌گیرد. تفاوت در این الگوریتم‌ها در مرحله آغازین و شرط همگرایی الگوریتم‌ها است ولی در بقیه مراحل و محاسبات مانند یکدیگر عمل می‌کنند. به همین علت همگی را الگوریتم‌های خوشه‌بندی k-میانگین می‌نامند.

روش خوشه‌بندی k-میانگین

فرض کنید مشاهدات  که دارای d بعد هستند را باید به k بخش یا خوشه تقسیم کنیم. این بخش‌ها یا خوشه‌ها را با مجموعه‌ای به نام  می‌شناسیم. اعضای خوشه‌ها باید به شکلی از مشاهدات انتخاب شوند که تابع «مجموع مربعات درون خوشه‌ها» (within-cluster sum of squares- WCSS) که در حالت یک بعدی شبیه واریانس است، کمینه شود.

بنابراین، تابع هدف در این الگوریتم به صورت زیر نوشته می‌شود.

الگوریتم K-means

در اینجا منظور از  میانگین خوشه  و   تعداد اعضای خوشه iام است. البته می‌توان نشان داد که کمینه کردن این مقدار به معنی بیشینه‌سازی میانگین مربعات فاصله بین نقاط در خوشه‌های مختلف (between-Cluster sum of Squares- BCSS) است زیرا طبق قانون واریانس کل، با کم شدن مقدار WCSS، مقدار BCSS افزایش می‌یابد، زیرا واریانس کل ثابت است.

در ادامه به بررسی روش خوشه بندی k-میانگین به روش لوید-فورجی (استاندارد) و هارتیگان-ونگ می‌پردازیم.

خوشه‌بندی k-میانگین با الگوریتم لوید (Lloyd’s Algorithm)

به عنوان یک الگوریتم استاندارد برای خوشه‌بندی k-میانگین از الگوریتم لوید بخصوص در زمینه علوم کامپیوتر، استفاده می‌شود. ابتدا به علائمی که در این رابطه به کار می‌رود، اشاره می‌کنیم.

mj(i): میانگین مقدارهای مربوط به خوشه jام در تکرار iام از الگوریتم را با این نماد نشان می‌دهیم.

Sj(i): مجموعه اعضای خوشه jام در تکرار iام الگوریتم.

الگوریتم لوید را با توجه به نمادهای بالا می‌توان به دو بخش تفکیک کرد. ۱- بخش مقدار دهی ()، ۲- بخش به روز رسانی (Update Step). حال به بررسی مراحل اجرای این الگوریتم می‌پردازیم. در اینجا فرض بر این است که نقاط مرکزی اولیه یعنی  داده شده‌اند.

  1. بخش مقدار دهی: هر مشاهده یا شی را به نزدیکترین خوشه نسبت می‌دهیم. به این معنی که فاصله اقلیدسی هر مشاهده از مراکز، اندازه گرفته شده سپس آن مشاهده عضو خوشه‌ای خواهد شد که کمترین فاصله اقلیدسی را با مرکز آن خوشه دارد. این قانون را به زبان ریاضی به صورت  فرمول 2  می‌نویسیم.
  2. بخش به روز رسانی: میانگین خوشه‌های جدید محاسبه می‌شود. در این حالت داریم:  فرمول 3

توجه داشته باشید که منظور از Si(t| تعداد اعضای خوشه iام است. الگوریتم زمانی متوقف می‌شود که مقدار برچسب عضویت مشاهدات تغییری نکند. البته در چنین حالتی هیچ تضمینی برای رسیدن به جواب بهینه (با کمترین مقدار برای تابع هزینه) وجود ندارد. کاملا مشخص است که در رابطه بالا،‌ فاصله اقلیدسی بین هر نقطه و مرکز خوشه ملاک قرار گرفته است. از این جهت از میانگین و فاصله اقلیدسی استفاده شده که مجموع فاصله اقلیدسی نقاط از میانگینشان کمترین مقدار ممکن نسبت به هر نقطه دیگر است.

نکته: ممکن است فاصله اقلیدسی یک مشاهده از دو مرکز یا بیشتر، برابر باشد ولی در این حالت آن شئ فقط به یکی از این خوشه‌ها تعلق خواهد گرفت.

تصویر زیر یک مثال برای همگرایی الگوریتم لوید محسوب می‌شود که مراحل اجرا در آن دیده می‌شود. همانطور که مشخص است الگوریتم با طی ۱۴ مرحله به همگرایی می‌رسد و دیگر میانگین خوشه‌ها تغییری نمی‌یابد. البته ممکن است که این نقاط نتیجه تابع هزینه را بطور کلی (Global) کمینه نکنند زیرا روش k-میانگین بهینه‌سازی محلی (Local Optimization) را به کمک مشتق‌گیری و محاسبه نقاط اکستریمم اجرا می‌کند.

 

K-means_convergence

همگرایی الگوریتم k-میانگین

 

نکته: به نقاط مرکزی هر خوشه مرکز (Centroid) گفته می‌شود. ممکن است این نقطه یکی از مشاهدات یا غیر از آن‌ها باشد. مشخص است که در الگوریتم لوید، k مشاهده به عنوان مرکز خوشه‌ها (Centroids) در مرحله اول انتخاب شده‌اند ولی در مراحل بعدی، مقدار میانگین هر خوشه نقش مرکز را بازی می‌کند.

خوشه‌بندی k-میانگین با الگوریتم هارتیگان-ونگ (Hartigan-Wong)

یکی از روش‌های پیشرفته و البته با هزینه محاسباتی زیاد در خوشه‌بندی k-میانگین، الگوریتم هارتیگان-ونگ است. برای آشنایی با این الگوریتم بهتر است ابتدا در مورد نمادهایی که در ادامه خواهید دید توضیحی ارائه شود.

فرمول 4  از این نماد برای نمایش «تابع هزینه» برای خوشه فرمول 5 استفاده می‌کنیم. این تابع در خوشه‌بندی k-میانگین برابر است با:

فرمول 6

 

فرمول 5 : از آنجایی که هدف از این الگوریتم، تفکیک اشیاء به k گروه مختلف است، گروه‌ها یا خوشه‌ها در مجموعه‌ای با نام S قرار دارند و داریم، فرمول 7

فرمول 8: برای نمایش میانگین خوشهjام از این نماد استفاده می‌شود. بنابراین خواهیم داشت:

فرمول 9

فرمول 11این نماد تعداد اعضای خوشه jام را نشان می‌دهد. بطوری که فرمول 10  است. البته مشخص است که در اینجا تعداد خوشه‌ها را با k‌ نشان داده‌ایم.

مراحل اجرای الگوریتم

در خوشه‌بندی k-میانگین با الگوریتم هارتیگان می‌توان مراحل اجرا را به سه بخش تقسیم کرد: ۱- بخش مقدار دهی اولیه (Assignment Step(   ،- ۲ بخش به روز رسانی (Update Step)، ۳- بخش نهایی (Termination). در ادامه به بررسی این بخش‌ها پرداخته می‌شود.

  1. بخش مقدار دهی اولیه: در الگوریتم هارتیگان-ونگ، ابتدا مشاهدات و یا اشیاء به طور تصادفی به k گروه یا خوشه تقسیم می‌شوند. به این کار مجموعه S با اعضایی به صورت فرمول 12  مشخص می‌شود.
  2. بخش به روز رسانی: فرض کنید که مقدارهای n و m از اعداد ۱ تا k انتخاب شده باشد. مشاهده یا شیئ از خوشه nام را در نظر بگیرید که تابع  فرمول 13 را کمینه سازد، در چنین حالتی مقدار x از خوشه nام به خوشه mام منتقل می‌شود. به این ترتیب شی مورد نظر در  فرمول 20 قرار گرفته و خواهیم داشت  فرمول 15 .
  3. بخش نهایی: زمانی که به ازای همه n,m,x مقدار  فرمول 16  بزرگتر از صفر باشد، الگوریتم خاتمه می‌یابد.

نکته: منظور از نماد  فرمول 17  محاسبه تابع هزینه در زمانی است که مشاهده x از مجموعه  فرمول 18  خارج شده باشد. همچنین نماد  فرمول 19 به معنی محاسبه تابع هزینه در زمانی است که مشاهده x به خوشه  فرمول 20  اضافه شده باشد.

در تصویر زیر مراحل اجرای الگوریتم هارتیگان به خوبی نمایش داده شده است. هر تصویر بیانگر یک مرحله از اجرای الگوریتم است. نقاط رنگی نمایش داده شده، همان مشاهدات هستند. هر رنگ نیز بیانگر یک خوشه است.

در تصویر اول مشخص است که در بخش اول از الگوریتم به طور تصادفی خوشه‌بندی صورت پذیرفته. ولی در مراحل بعدی خوشه‌ها اصلاح شده و در انتها به نظر می‌رسد که بهترین تفکیک برای مشاهدات رسیده‌ایم.

در تصویر آخر نیز مشخص است که مراکز خوشه‌ها، محاسبه و ثابت شده و دیگر بهینه‌سازی صورت نخواهد گرفت. به این ترتیب پاسخ‌های الگوریتم با طی تکرار ۵ مرحله به همگرایی می‌رسد.

 

hartigan-step-1

الگوریتم هارتیگان بخش مقدار دهی اولیه

hartigan-step-2

الگوریتم هارتیگان تکرار 1

 

hartigan-step-3

الگوریتم هارتیگان تکرار 2

 

hartigan-step-5

الگوریتم هارتیگان تکرار 3

 

hartigan-step-4

الگوریتم هارتیگان تکرار 4

 

hartigan-step-6

الگوریتم هارتیگان تکرار 5

 

اجرای این الگوریتم‌ها با استفاده از دستورات زبان برنامه‌نویسی R

برای استفاده از دستورات و فرمان‌های مربوط به خوشه‌بندی k-میانگین، باید بسته یا Package مربوط به خوشه‌بندی kmeans به اسم stats را در R نصب کرده باشد. البته از آنجایی این بسته بسیار پرکاربرد است،‌ معمولا به طور خودکار فراخوانی شده است. کدهای زیر نشانگر استفاده از الگوریتم خوشه‌بندی توسط روش‌های مختلف آن است.

library(stats)
data=iris[,1:4]
method=c("Hartigan-Wong", "Lloyd",
"MacQueen")
k=3
kresults1=kmeans(data,k,algorithm = method[1])
kresults2=kmeans(data,k,algorithm=method[2])
kresults3=kmeans(data,k,algorithm=method[3])

kresults1
kresults2
kresults3
با توجه به داده‌های iris که مربوط به اندازه و ابعاد کاسبرگ و گلبرگ سه نوع گل مختلف است، خوشه‌بندی به سه دسته انجام شده است. اطلاعات مربوط به ۱۰ سطر اول این مجموعه داده،‌ به صورت زیر است.

با اجرای کدهای نوشته شده، خوشه‌بندی انجام شده و نتابج تولید می‌شوند. به عنوان مثال می‌توان خروجی را برای kresult1 که انجام خوشه بندی توسط الگوریتم هارتیگان است به صورت زیر مشاهده کرد:

iris clustering

همانطور که دیده می‌شود، در سطر اول تعداد اعضای هر خوشه، نمایش داده شده است. در بخش دوم که با سطر ۱ و ۲ و ۳ مشخص شده،‌ مراکز هر سه خوشه برحسب ویژگی‌های (طول و عرض کاسبرگ و طول و عرض گلبرگ) محاسبه شده و در قسمت Cluster Vector نیز برچسب خوشه هر کدام از مشاهدات دیده می‌شود. در انتها نیز مجموع مربعات فاصله درون خوشه‌ای (مجموع فاصله هر مشاهده از مرکز خوشه) استخراج شده و درصد یا شاخص ارزیابی خوشه‌بندی بر اساس نسبت مربعات بین خوشه‌ها به مربعات کل دیده می‌شود. این مقدار برای این حالت برابر ۸۸.۴٪ است که نشان می‌دهد بیشتر پراکندگی (total_ss) توسط پراکندگی بین خوشه‌ها (between_ss) بیان شده است. پس به نظر خوشه‌بندی مناسب خواهد بود. پس اختلاف بین گروه‌ها ناشی از خوشه‌های است که مشاهدات را به دسته‌‌های جداگانه تفکیک کرده.

همچنین در کدها مشخص است که تعداد خوشه‌های در متغیر k ثبت و به کار رفته است. در شکل دیگری از دستور kmeans می‌توان به جای معرفی تعداد خوشه‌ها از مراکز دلخواه که با تعداد خوشه‌ها مطابقت دارد، استفاده کرد. برای مثال اگر برنامه به صورت زیر نوشته شود، الگوریتم ابتدا نقاط معرفی شده را به عنوان نقاط مرکزی (Centroids) به کار گرفته و سپس مراحل بهینه سازی را دنبال می‌کند. از آنجا که سه نقطه مبنا قرار گرفته، الگوریتم متوجه می‌شود که باید مشاهدات به سه خوشه تفکیک شود.

 

library(stats)
data=iris[,1:4]
method=c("Hartigan-Wong", "Lloyd",
         "MacQueen")
c1=c(6,4,5,3)
c2=c(5,3,1,0)
c3=c(6,2,4,2)
centers=rbind(c1,c2,c3)
kresults1=kmeans(x = data,centers = centers,algorithm = method[1])
kresults2=kmeans(x = data,centers = centers,algorithm=method[2])
kresults3=kmeans(x = data,centers = centers,algorithm=method[3])

kresults1
kresults2
kresults3
در تصویر زیر نتیجه خوشه بندی k-میانگین را برای داده‌های iris توسط یک نمودار مشاهده می‌کنید. البته باید توجه داشت که این نمودار دو بعدی است در حالیکه داده‌ها، دارای چهار ویژگی هستند. به کمک روش‌های آماری مانند تجزیه به مولفه‌های اصلی (PCA) ابعاد مسئله کاهش یافته تا در سه بعد روی نمودار نمایش داده شود. سمت راست تصویر گروه‌های واقعی و سمت چپ نتیجه خوشه‌بندی دیده می‌شود. نقاطی که در خوشه‌ها به درستی تشخیص داده نشده‌اند، باعث افزایش خطای خوشه‌بندی خواهند شد.

کاربردها

از الگوریتم خوشه‌بندی k-میانگین در «بخش‌بندی بازار کسب و کار» (market Segmentation)، «دسته‌بندی مشتریان» (Customer Segmentation)، «بینایی رایانه‌ای» (Computer Vision) و «زمین‌آمار (Geostatistics) استفاده می شود. برای مثال در تشخیص تعداد رنگ و یا فشرده سازی تصاویر برحسب رنگ‌ها می‌توان از این الگوریتم‌ها استفاده کرد.

 

در تصویر بالا گل رز زرد رنگی دیده می‌شود که در یک محیط سبز قرار گرفته است. با استفاده از الگوریتم‌های خوشه‌بندی می‌توان تعداد رنگ‌ها را کاهش داده و از حجم تصاویر کاست. در تصویر زیر دسته بندی رنگ‌های گل رز دیده می‌شود.

 

 

در این تصویر، هر طیف رنگ براساس میزان رنگ قرمز و سبز، بوسیله «سلول‌های ورونوی» (Voronoi Cell) تقسیم‌بندی شده است. این تقسیم‌بندی می‌تواند توسط الگوریتم‌ها خوشه‌بندی k-میانگین صورت گرفته باشد. در کل تصویر نیز، طیف رنگ‌های مختلف برای تصویر گل رز در یک «نمودار ورونوی» (Voronoi diagram) نمایش داده شده است که خوشه‌ها را بیان می‌کند.

 

خوشه بندی k میانگین (k-means Clustering) قسمت 1
خوشه بندی k میانگین (k-means Clustering) قسمت 2

/0 دیدگاه /توسط